9.методы деления чисел с фиксированной запятой в прямых кодах и дополнительных (обратных) кодах.

Привет, Вы узнаете о том , что такое методы деления чисел с фиксированной запятой в прямых кодах, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое методы деления чисел с фиксированной запятой в прямых кодах, дополнительных обратных кодах , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

Аннотация: В лекции даны методы деления чисел с фиксированной запятой в прямых кодах и дополнительных (обратных) кодах. Описаны операции над числами с плавающей запятой – умножение, деление, сложение, вычитание.

Реализация операции деления в ЭВМ в двоичной системе счисления выполняется проще, чем в десятичной. Это объясняется тем, что при определении каждой цифры частного нужно сделать только одну пробу.

Если числа X и Y заданы в прямом коде, и они представлены с фиксированной запятой, то для выполнения деления используются два основных алгоритма:

• со сдвигом и автоматическим восстановлением остатка ;
• со сдвигом делителя и автоматическим восстановлением остатка.

Пусть: [X]_пк = sign X. x₁x₂..x_n

[Y]_пк = sign Y. y₁y₂..y_n

[Z]_пк = [X]_пк/[Y]_пк = sign Z. z₁z₂..z_n

X и Y должны быть такими, чтобы:

|Z| < 1 (то есть фиксированная запятая )

Деление в прямом коде со сдвигом и автоматическим восстановлением остатка

1. 
2. 

3. Если , то z₀ = 1 и  ( z₀ – целая часть результата).

    

   Если , то z₀ = 0 и 

    

и т. д.

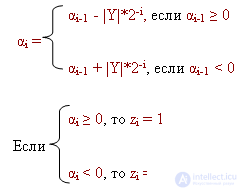
Пример:

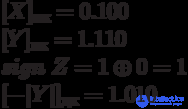
₊0.100 = [|X|]_дк

1.010 = [-|Y|]_дк

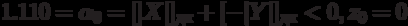
0.110 = [|Y|]_дк

1.010 = [-|Y|]_дк

0.110 = [|Y|]_дк

Ответ: [Z]_пк = 1.101

Деление в прямом коде со сдвигом делителя и автоматическим восстановлением остатка

• 
• 

• Если , то z₀ = 1.

   

  Если , то z₀ = 0.

   
  
   

Разрядная сетка (n + d) разрядов, где d = log₂n

Пример:

1) [X]

 = 1.1001
2) [Y]

 = 1.1011
n = 4, d = 2

Ответ: [Z]_пк = 0.1100

Пример:

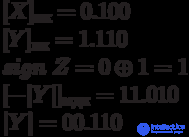
Ответ: [Z]_пк = 1.101

Деление в дополнительном (обратном) кодах со сдвигом и автоматическим восстановлением остатка

[X]_дк,ок ; [Y]_дк,ок

Деление в ОК не применяется, так как "0" в ОК имеет двойное изображение. В первом такте вместо  берется sign X, а вместо  берется [X]_дк,ок

Пример:

[X]

 = 1.0111 
[Y]

 = 1.0011 
Т.к. sign X = sign Y,то

₊1.0111 | 1.0011

0.1101 = -[Y]_дк

______

1.0011 = [Y]_дк

______

0.1101 = +[-[Y]_дк ]_дк

______

1.0011 = [Y]_дк

______

0.1101 = +[-[Y]_дк ]_дк

______

Ответ: [Z]_дк = 0.1011

Это справедливо при 0 <= [Z]_дк = [X]_дк / [Y]_дк ]| < 1.

Если необходимо определить частное |[Z]_дк = [X]_дк / [Y]_дк | | < 2, то поступают так:

[X]_дк*2^-1 / [Y]_дк = z₀z₁z₂...z_n, z₀ – знак, z₁ – целая часть числа.

Арифметические операции над числами, представленными с плавающей запятой

В основе арифметических операций над числами с плавающей запятой лежат принципы, на которых базируются операции над числами сфиксированной запятой. Об этом говорит сайт https://intellect.icu . При этом есть и некоторые особенности.

Будем условно считать, что порядки заданы в обратном коде, а мантиссы – в прямом.

Умножение:

X = 2

 * sign X.x

x

...x

Y = 2

 * sign Y.y

y

...y

Z = X*Y = 2

 * sign Z.z

z

...z

Порядок выполнения операции следующий:

1. Знак произведения находится так же, как и при умножении чисел с фиксированной запятой:

    
2. Порядок произведения находится алгебраическим суммированием порядков мно­жимого и множителя.

3. Мантисса находится по правилам умножения чисел с фиксированной запятой.

    

   При этом возможны следующие случаи:

    

   • Мантисса произведения – ненормализованное число, так как

      
     

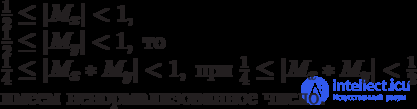
     Поэтому необходима нормализация влево максимум только на один разряд.

      

     С этой целью нужно сдвинуть мантиссу влево на один разряд. Это соответствует умножению числа на 2¹. Для того чтобы число не увеличилось в два раза, нужно из порядка вычесть единицу.

      

   • При умножении двух чисел в силу ограниченности разрядной сетки можно получить число, которое не может быть в ней представлено. Это соответствует получению машинной бесконечности.

      

     В данном случае вырабатывается специальный признак, по которому дальнейшие вычисления прекращаются.

      

   • При умножении двух чисел можно получить минимальное число, которое также не может быть представлено в разрядной сетке. Это соответствует случаю, когда получаемое число должно быть интерпретировано как нуль.

      
    

Деление

В основном аналогично умножению:

X = 2

 * sign X.x

x

...x

Y = 2

 * sign Y.y

y

...y

Z = X/Y = 2

 * sign Z.z

z

...z

Порядок выполнения операции следующий:

1. Находится по известным правилам знак частного.
2. Порядок частного находится как разность порядков делимого и делителя.

3. Цифры частного находятся так:

    

   вначале находится целая часть мантиссы, то есть 

    

   Если , если , то z₀ = 0.

    

Дробная часть мантиссы находится так же, как при операциях над числами с фиксированной запятой. Такой порядок действий вытекает из того, что:

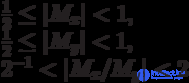
То есть, возможно получение ненормализованной мантиссы. Для нормализации мантиссу необходимо сдвинуть вправо на один разряд и, чтобы не уменьшать при этом результат в два раза, нужно прибавить к порядку одну единицу.

При делении, так же, как и при умножении, возможно получение кода машинного нуля и кода бесконечности.

Сложение и вычитание

Обе операции выполняются по сходным алгоритмам.

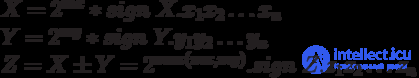
Операция выполняется следующим образом:

1. Находится разность порядков: 
2. Производится выравнивание порядков, при этом если разность порядков положительна, то в качестве порядка результата берется m_x, а мантисса M_y сдвигается вправо на |m_x– m_y| разрядов; еcли разрядность порядков отрицательна, то денормализуется мантисса M_x.
3. Производится алгебраическое суммирование мантисс слагаемых.
4. Выполняется нормализация влево или вправо на соответствующее число разрядов с необходимым исправлением порядка.

Пример:

порядок       мантисса
[m

]

 = 0.11 [M

]

 = 0.1010
[m

]

 = 0.10 [M

]

 = 0.1110
Находим разность порядков:
    

00.11 = [m

]

     11.01 = [-m

]

  1| 00.00
   |_ _->1

00.01 =  - разность порядков.

Так как m x > m

, то:
        

00.1010 = [M

]

         00.0111 = [M

]

 * 2

[Z]мок = 01.0001 – переполнение
         2

 * [Z]

 = 00.1000 – нормализация
                max(m

,m

) = [m

]

 = 

00.11
                              [1]

 = 00.01
                             [m

]

 = 01.00 – переполнение порядка

Z = .

При выполнении операции сложения возможны следующие специфические случаи, называемые блокировками:

а) При определении разности порядков может оказаться, что необходимо мантиссу одного из чисел сдвигать на величину, большую, чем число разрядов в разрядной сетке. В этом случае, естественно, такое число может быть воспринято как нуль, а операция дальнейшего сложения может блокироваться, то есть не выполняться.

В качестве результата берется максимальное число.

Пример:

[m

]

 = 0.101 [M

]

 = 0.10111101
[m

]

 = 1.001 [M

]

 = 0.10000001

Разность порядков:

00.101 = [m

]

 00.110 = [-m

]

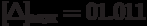 – то есть это число 11 ₁₀ , а в разрядной сетке мантиссы только 8 разрядов.

Поэтому операция блокируется, а результатом является число:

[m

] = 0.101 [M

] = 0.10111101

Аналогичный случай может быть, когда разность порядков – отрицательна (отрицательное переполнение). В этом случае операция также блокируется, а результатом будет число с максимальным порядком.

Пример:

[m

]

 = 1.010 [M

]

 = 1.10101011
[m

]

 = 0.110 [M

]

 = 1.11111111

Разность порядков:

  11.010 = [m

]

   11.001 = [-m

]

   _______

1| 10.011
         1
   _______

10.100 = 

То есть разность порядков меньше (-8).

Операция блокируется, а результатом будет число:

[m

]

 = 0.110 [M

]

 = 1.11111111

Десятичные двоично-кодированные системы.

Иногда в ЭВМ используются десятичные системы счисления. Их выгодно использовать тогда, когда объем исходных данных для обработки на ЭВМ – велик, сама обработка производится по относительно несложным программам. На этом происходит значительная экономия времени, которая вытекает из того, что не нужно делать перевод из десятичной в двоичную систему и обратно.

Как правило, в состав оборудования таких ЭВМ вводится АУ, работающее с числами в десятичной системе счисления. Поскольку в качестве основного запоминающего элемента используется триггер-ячейка с двумя устойчивыми состояниями, то каждая десятичная цифра кодируется совокупностью двоичных символов.

Перевод чисел из десятичной системы в десятичную двоично-кодированную выполняется исключительно просто, поразрядно и одновременно по всей сетке:

879,65_10 -> 1000 0111 1001, 0110 010110^-2

Аналогично, выполняется и обратный перевод:

0110 1001, 0101 0011

 -> 69, 53

Существует большое разнообразие десятичных двоично-кодированных систем. Это многообразие вытекает из избыточности двоичного кода, при котором из 16 возможных комбинаций в каждом разряде используется по прямому информационному назначению лишь 10.

Наиболее широкое применение находят системы кодирования 8421 и 8421⁺³ (код Штибитца).

Система 8421 – неудобна тем, что при выполнении операции вычитания нет прямого перехода от цифры каждого разряда кдополнительному коду.

0000 - 0

0001 - 1

0010 - 2

0011 - 3

0100 - 4

0101 - 5

0110 - 6

0111 - 7

1000 - 8

1001 - 9

В то же время эта система обладает свойством аддитивности , поскольку результаты операции сложения над числами в десятичной системе и над их изображением в системе 8421 – совпадают.

Система 8421⁺³ - более интересна, т.к. она обладает свойством самодополнения. Видно, что дополнение до 9 можно получить, применяя операцию поразрядного инвертирования кода.

0011 – 0

0100 – 1

0101 – 2

0110 – 3

0111 – 4

1000 – 5

1001 – 6

1010 – 7

1011 – 8

1100 – 9

Всего существует А₁₆¹⁰ = 2,9•10¹⁰ вариантов 10-ых двоично-кодированных систем.

Выводы из данной статьи про методы деления чисел с фиксированной запятой в прямых кодах указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое методы деления чисел с фиксированной запятой в прямых кодах, дополнительных обратных кодах и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ