Полусумматор - принцип работы, обозначение, применение

Привет, Вы узнаете о том , что такое полусумматор , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое полусумматор , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

Полусумма́тор — комбинационная логическая схема, имеющая два входа и два выхода (двухразрядный сумматор, бинарный сумматор).

полусумматор (или half-adder) — это комбинационная логическая схема, выполняющая сложение двух одноразрядных двоичных чисел. Он имеет два входа, которые представляют слагаемые, и два выхода: один для суммы и другой для переноса.

Полусумматор позволяет вычислять сумму A+B, где A и B — это разряды (биты) обычно двоичного числа, при этом результатом будут два бита S и C, где S — это бит суммы по модулю 2, а C — бит переноса.

Существуют сумматоры и полусумматоры работающие не в двоичной логике.

Отличается от полного сумматора тем, что не имеет входа переноса из предыдущего разряда. Для построения полного сумматора необходимо иметь дополнительный вход переноса из предыдущего разряда, таким образом, полный сумматор имеет 3 входа.

Двоичный полный сумматор строится из двух полусумматоров и логического элемента 2ИЛИ, именно поэтому рассматриваемая схема называется полусумматором.

Полусумматоры используется для построения полных сумматоров.

• 1642 год - француз Блез Паскаль изобрел механический десятичный полный (трехоперандный, с единицей переноса) сумматор и начал создавать суммирующую машину «Паскалину», первый разряд в которой был полусумматором (двухоперандным, без единицы переноса из предыдущего разряда). Из-за сложности французской денежной системы тех времен, в «Паскалине» были механические полусумматоры и других значностей ("-ичностей").
• 1673 год - Готфрид Лейбниц построил механический десятичный арифмометр Лейбница, первый разряд в котором был механическим десятичным полусумматором (двухоперандным, без единицы переноса из предыдущего разряда).
• 1939 год — Джордж Штибиц (Georg Stibits) из компании Bell Laboratories создал первый двоичный полусумматор «Model K Аdder» на двух электромеханических реле .
• 1958 год — в МГУ (мехмат) Н. П. Брусенцов построил первую электронную троичную ЭВМ «Сетунь» с первым электронным троичным полусумматором .

Стандартное изображение двоичного полусумматора по DIN 40900.

Полусумматор, реализованный на элементах ИСКЛЮЧАЮЩЕЕ ИЛИ и И.

Полусумматор, реализованный на элементах ИЛИ с инверсными входами и И.

Двоичный полусумматор может быть определен тремя способами:

1. табличным, в виде таблиц истинности,
2. аналитическим, в виде формул (СДНФ),
3. графическим, в виде логических схем.

Так как формулы и схемы могут преобразовываться в соответствии с алгеброй логики, то, одной таблице истинности двоичного полусумматора могут соответствовать множества различных формул и схем. Поэтому, табличный способ определения двоичного полусумматора является основным.

Двоичный полусумматор формирует две бинарные (двухоперандные) двоичные логические функции: это сумма по модулю два, иначе эта функция называется ИСКЛЮЧАЮЩЕЕ ИЛИ (XOR) — формирует бит суммы S и функция И (AND) - формирует бит переноса C.

S

C

или в другом виде:

Ненулевой перенос образуется в 1-м случае из 4-х.

СДНФ суммы по модулю 2:

СДНФ бита переноса:

Демонстрационный полусумматор Штибица «Model K Аdder» используется в учебных целях и состоит: из двух последовательно соединенных гальванических элементов, по 1,5 Вольта каждый, с суммарным напряжением 3 Вольта, двух кнопок для ввода двух битов аргументов A и B, двух электромагнитных реле, выполняющих бинарную двоичную логическую функцию сложения по модулю 2 и бинарную двоичную логическую функцию бита переноса при двоичном сложении, и двух лампочек накаливания с напряжением 3 Вольта для индикации бита суммы по модулю 2 (S) и бита переноса (C)

Так как существуют две троичных системы счисления — несимметричная, в которой в разряде переноса не бывает значения больше «1» и симметричная (Фибоначчи), в которой в разряде переноса возможны все три состояния трита, и, как минимум, три физических реализации троичных систем — трехуровневая однопроводная, двухуровневая двухпроводная (BCT) и двухуровневая трехбитная одноединичная, то и троичных полусумматоров может быть большое множество.

Троичный полусумматор в несимметричной троичной системе счисления представляет собой объединение двух бинарных троичных логических функций — «сложение по модулю 3» и «разряд переноса при троичном сложении».

S

C

или в другом виде:

Троичный полусумматор в симметричной троичной системе счисления является также и полувычитателем и представляет собой объединение двух бинарных троичных логических функций — «младший разряд (трит) суммы-разности» и «старший разряд (трит) суммы-разности (разряд переноса при сложении-вычитании в троичной симметричной системе счисления)».

S

C

или в другом виде:

Цифра «7» здесь обозначает «-1»

Ненулевой перенос образуется в 2-х случаях из 9-ти. Об этом говорит сайт https://intellect.icu .

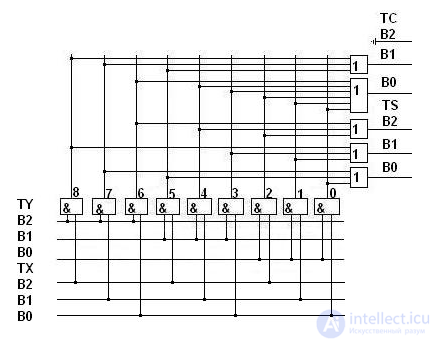
Троичный полусумматор.

На рисунке приведена схема троичного несимметричного полусумматора в трехбитной одноединичной системе троичных логических элементов, описанного в .

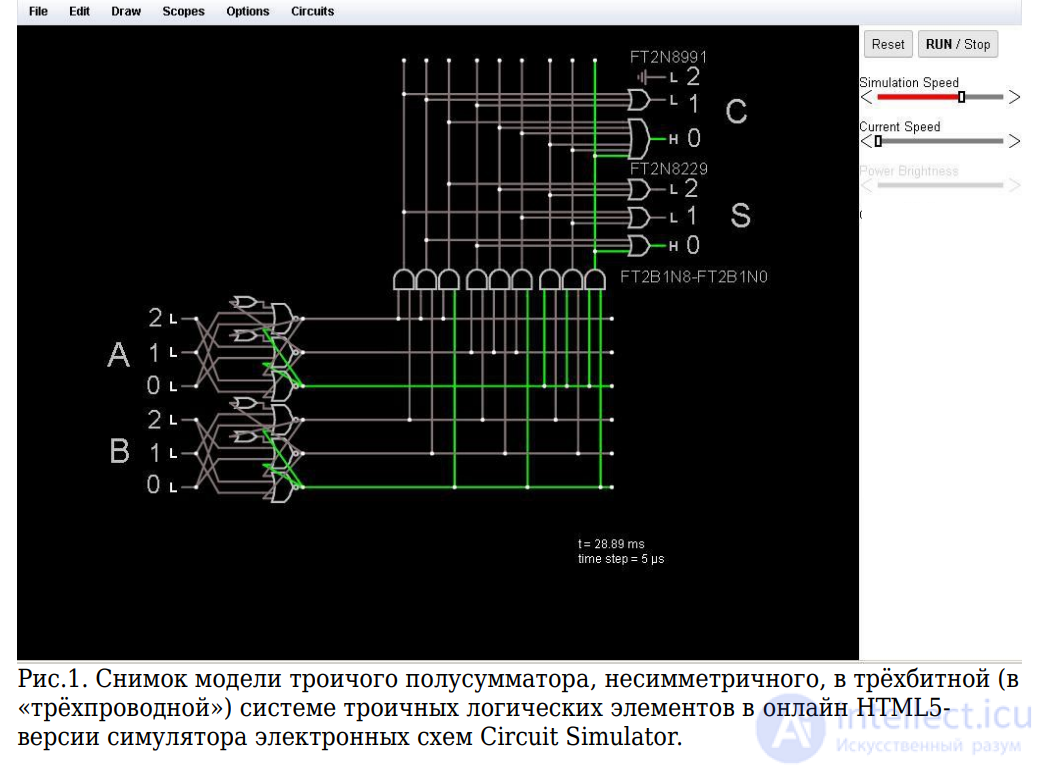
Троичный зеркально-симметричный одноразрядный полусумматор смоделирован ниже.

Состоит из двух таблиц размером 10х10. Первая таблица — суммы по модулю 10, вторая таблица — единицы переноса при бинарном (двухоперандном) десятичном сложении.

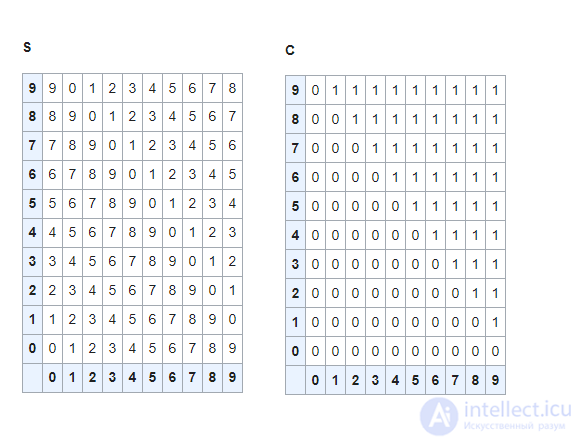
Одноразрядное двухоперандное (двухаргументное) десятичное сложение является одной из бинарных (двухаргументных, двухоперандных, двухвходовых) десятичных логических функций с бинарным (двухразрядным) результатом, имеющей кроме собственного номера и собственное название словами: "одноразрядный десятичный полусумматор".

Десятичной функцией в теории функциональных систем и в десятичной логике называют функцию типа , где D={0,1,2,3,4,5,6,7,8,9} — десятичное множество, а n — неотрицательное целое число, которое называют арностью или местностью функции.

Всего существует простейших бинарных с бинарным (двухразрядным) результатом десятичных логических функций (2 децита -> 2 децита), где m - количество аргументов функции (входная "-арность"), а n - количество результатов действия функции (выходная "-арность"), что больше всех больших чисел Дирака вместе взятых и числа Шеннона (оценочное минимальное количество неповторяющихся шахматных партий, вычисленное в 1950 году американским математиком Клодом Шенноном, составляет приблизительно 10120) впридачу.

Одноразрядное двухоперандное (двухаргументное) десятичное сложение можно также представить, как комбинацию (объединение двух) бинарных (двухаргументных, двухоперандных, двухвходовых) десятичных логических функцией с унарным (одноразрядным) результатом, имеющих кроме собственных номеров и собственные названия словами: "одноразрядное десятичное бинарное сложение по модулю 10" и "единица переноса в следующий разряд при одноразрядном десятичном бинарном сложении".

Всего существует простейших бинарных с унарным (одноразрядным) результатом десятичных логических функций (2 децита -> 1 децит).

Номер функции "одноразрядное десятичное бинарное сложение по модулю 10" содержит все значения функции при переборе значений аргументов от 0 до 9 и относительно просто получается из таблицы десятичного полусумматора: 8765432109 7654321098 6543210987 5432109876 4321098765 3210987654 2109876543 1098765432 0987654321 9876543210 (пробелы отделяют по 10 знаков в номере функции).

Номер функции "единица переноса в следующий разряд при одноразрядном десятичном бинарном сложении" содержит все значения функции при переборе значений аргументов от 0 до 9 и тоже относительно просто получается из таблицы десятичного полусумматора: 1111111110 1111111100 1111111000 1111110000 1111100000 1111000000 1110000000 1100000000 1000000000 0000000000 (пробелы отделяют по 10 знаков в номере функции).

Так как в разряде переноса не бывает значения больше 1, то разряд переноса в одноразрядном десятичном полусумматоре является более простой десятичной функцией с унарным (одноразрядным) двоичным результатом (2 децита -> 1 бит).

'Half Adder Decimal Single-Digit
CLS
DATA 0,1,2,3,4,5,6,7,8,9
DATA 1,2,3,4,5,6,7,8,9,0
DATA 2,3,4,5,6,7,8,9,0,1
DATA 3,4,5,6,7,8,9,0,1,2
DATA 4,5,6,7,8,9,0,1,2,3
DATA 5,6,7,8,9,0,1,2,3,4
DATA 6,7,8,9,0,1,2,3,4,5
DATA 7,8,9,0,1,2,3,4,5,6
DATA 8,9,0,1,2,3,4,5,6,7
DATA 9,0,1,2,3,4,5,6,7,8

DATA 0,0,0,0,0,0,0,0,0,0
DATA 0,0,0,0,0,0,0,0,0,1
DATA 0,0,0,0,0,0,0,0,1,1
DATA 0,0,0,0,0,0,0,1,1,1
DATA 0,0,0,0,0,0,1,1,1,1
DATA 0,0,0,0,0,1,1,1,1,1
DATA 0,0,0,0,1,1,1,1,1,1
DATA 0,0,0,1,1,1,1,1,1,1
DATA 0,0,1,1,1,1,1,1,1,1
DATA 0,1,1,1,1,1,1,1,1,1

DEFINT I,J,F,A,B
FOR I=0 TO 9
  FOR J=0 TO 9
    READ F2DSM[I,J]  'Function 2-argument Decimal Summ Mod 10 NonSymmetric
  NEXT J
NEXT I
FOR I=0 TO 9
  FOR J=0 TO 9
    READ F2DC[I,J]   'Function 2-argument Decimal Carry Summ 10 NonSymmetric
  NEXT J
NEXT I

A=9
B=9
PRINT USING "#";A;
PRINT " + ";
PRINT USING "# = ";B;
PRINT USING "#";F2DC[A,B];
PRINT USING "#";F2DSM[A,B]
END

Состоит из двух таблиц размером 16х16. Первая таблица — суммы по модулю 16, вторая таблица — единицы переноса при бинарном (двухоперандном) шестнадцатиричном сложении.

• Сумматор

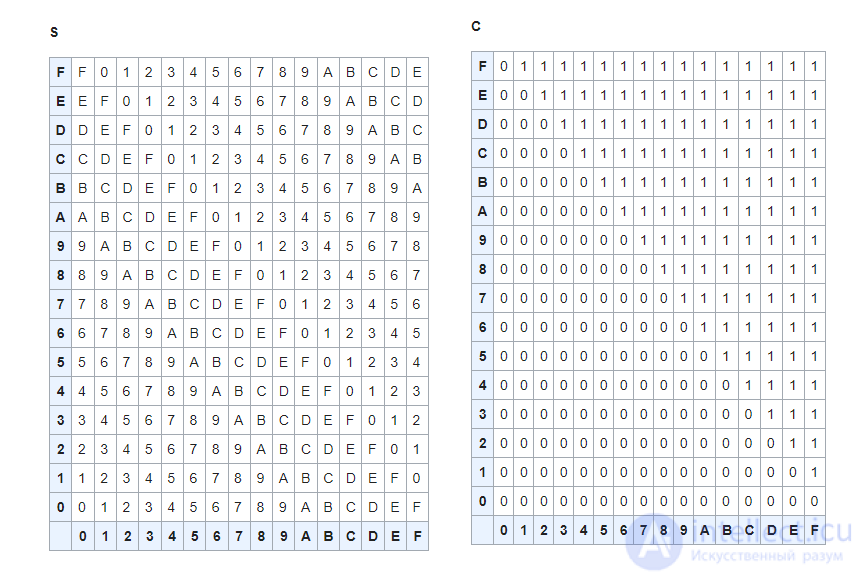
Исследование, описанное в статье про полусумматор , подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое полусумматор и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ