5: Минимизация неполностью определенных функций

Привет, Вы узнаете о том , что такое минимизация неполностью определенных функций, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое минимизация неполностью определенных функций , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

Аннотация: В лекции представлена минимизация неполностью определенных функций , дан синтез функций в базисах штрих Шеффера и стрелка Пирса, даны подходы к минимизации конъюнктивных форм.

Очень часто, если не в большинстве случаев, работа конкретного устройства описывается с помощью неполностью определенной функции, так как некоторые комбинации входных сигналов не подаются или являются запрещенными.

Определение. Неполностью определенной функцией является такая переключательная функция, значения которой на некоторых наборах аргументов могут быть произвольными (т.е. равными " 0 " или " 1 ").

Определение. Пусть функция f(x₁,x₂,...x_n) не определена на " р " наборах аргументов. Тогда полностью определенную функцию 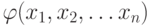 будем считать эквивалентной к f(x₁,x₂,...x_n), если ее значения на тех наборах, на которых f(x₁,x₂,...x_n)определена, совпадают.

Очевидно, существует 2^р различных функций, эквивалентных f(x₁,x₂,...x_n).

Задача минимизации f(x₁,x₂,...x_n) состоит в выборе такой эквивалентной 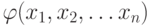, которая имеет простейшую форму.

Введем две вспомогательные эквивалентные функции , , 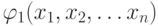которые принимают на запрещенных наборах аргументов значения 0 и 1 соответственно.

ТЕОРЕМА. СДНФ неполностью определенной f(x₁,x₂,...x_n) совпадает с дизъюнкцией самых коротких импликант 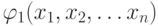, которые совместно накрывают все конституенты единицы , и ни одна из которых не является лишней.

Пример:

Пусть задана f(x₁,x₂,...x_n) в виде следующей таблицы:

Тогда

,

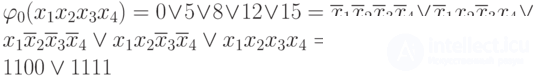а

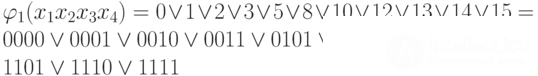
Найдем простые импликанты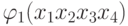 

Конституенты единицы  1	Отметки о склейке	Импликанты	Отметки о склейке	Импликанты
0000	*	000- 00-0 -000	*	00- - 00- - -0-0
0001 0010 1000	*		*
	*		*
	*	00-1 0-01 001- -010 1-00	*
0011 0101 1010 1100	*		-
	*		*	1- -0
	*		*
	*		*
1101 1110	*	-101 1-10 110- 11-0	-
			*
	*		-	11- -
			-
1111	*	111-	*

Простые импликанты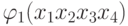 

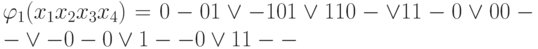
Построим импликантную матрицу.

Конституенты единицы	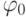0000	0101	1000	1100	1111
Простые импликанты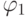
0-01		+
-101		+
110-				+
11-0				+
00--	+
-0-0	+		+
1--0			+	+
11--				+	+

Выполним оптимальное покрытие конституент единицы 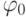 простыми импликантами  и получаем минимальную форму функцииf(x₁x₂ x₃ x₄)

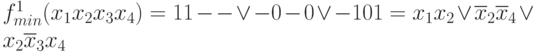
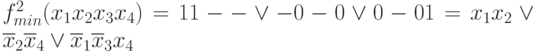
Минимизация с помощью диаграмм Вейча неполностью определенных функций в наглядной и удобной форме позволяет отыскать минимальные формы.

Пример:

Рассмотрим функцию f(x₁x₂ x₃ x₄) и найдем ее минимальную форму. Об этом говорит сайт https://intellect.icu . Заполнить диаграмму Вейча по следующим правилам: в клетки диаграммы поставим единицы, которые соответствуют конституентам единицы, нули – для отсутствующих конституент и символ неопределенности – " * " (звездочка) – в остальные.

Видно, что в клетки для конституент: x₁x₂x₃x₄, x₁x₂x₃x₄, x₁x₂x₃x₄ целесообразно "поставить" единицы вместо символов неопределенности, так как в этом случае образуется правильная конфигурация 2-го ранга, которая покрывается произведением x₂x₃.

Аналогично и в клетку x₁x₂x₃x₄ нужно "поставить" единицу.

Итак, .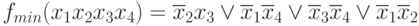

Замечание. Все, что было сказано относительно минимизации функции, представленной в СДНФ или ДНФ справедливо для функции, заданной в СКНФ или КНФ.

В этом случае необходимо отыскивать правильные конфигурации, образованные нулями

Синтез переключательных функций в одноэлементном базисе

Операция (стрелка) Пирса

f

(x

,x

)

Эту функцию можем представить, записав по "единицам":

или

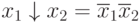
На основе принципа суперпозиции:

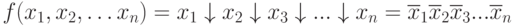
Применяя правило де Моргана:

или:

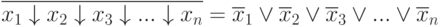
т.е.

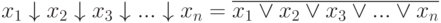
Рассмотрим некоторые соотношения для операции Пирса:

,

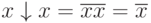
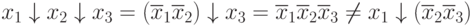т.е. операция Пирса не обладает свойством ассоциативности

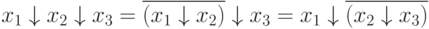
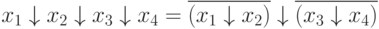
При этом порядок выполнения операций в формулах, где есть операции Пирса такой:

1. раскрываются скобки
2. выполняются операции инверсии
3. выполняются операции Пирса

Синтез логических функций в базисе Пирса удобно производить, имея запись функции в КНФ.

Допустим, что ФАЛ задана в конъюктивной форме

f = Q₁Q₂Q₃ . . . Q_n

Подставим член Q_i в виде:

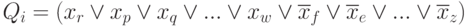
Возьмем двойное отрицание от обеих частей этого равенства, применив правило де Моргана

Применяя соотношение, полученное на основе принципа суперпозиции:

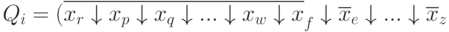
Или, применяя это преобразование к исходной форме, получим:

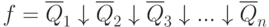
Итак: чтобы от КНФ перейти к базису Пирса и инверсии необходимо:

1. заменить операции дизъюнкции операциями Пирса
2. заменить операции конъюнкции операциями Пирса
3. заключить в скобки все те группы букв, которые соответсвуют конъюнктивным членам.

Пример:

Замечание. Так как в этих произведениях число букв не увеличивается, и если исходная форма функции была минимальной, то вновь полученная также будет минимальной (в действительности дело обстоит сложнее, поскольку мы рассматриваем не базис " 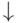 ", а другой, то есть "  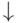" и " - " - операцию Пирса и инверсию).

Принципиально можно избавиться от отрицаний, применив соотношение: , но тогда нельзя будет утверждать, что полученная форма будет минимальной!

Операция штрих Шеффера

Заметим, что эта функция дуальна по отношению к f₈, поэтому все свойства являются по существу дуально вытекающими из рассмотренных.

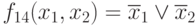 (запись функций по нулям)

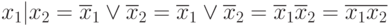
на основе принципа суперпозиции:

x₁ | x₂ | . . . | x_n = x₁x₂...x_n

Рассмотрим некоторые эквивалентности:

x₁ | x₂ | x₃ = (x₁ x₂)| x₃ = x₁| (x₂ x₃)

x₁ | x₂ | x₃| x₄ = (x₁ x₂)| (x₃ x₄)

Сформулируем правила перехода от ДНФ функции к выражению с использованием операции " Штрих Шеффера ".

1. заменить все операции дизъюнкции на операции Шеффера
2. заменить все операции конъюнкции на операции Шеффера
3. группы букв, которые соответствуют дизъюнктивным членам, заключить в скобки.

Пример:

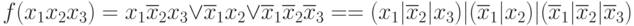
То же самое можно утверждать относительно минимальной формы.

В заключение необходимо отметить, что в настоящее время вопросы синтеза функций в одноэлементном базисе приобретают большое значение, так как соответствующие элементы используют операцию Пирса и Шеффера. Однако в полной мере теоретически методы синтеза разработаны не столь детально, как это сделано в базисе "и", "или", "инверсия".

Минимальные конъюнктивные нормальные формы

Как было отмечено, для получения минимальной формы функции нужно построить как МДНФ так и МКНФ.

Рассмотрим построение МКНФ.

В основном методы получения МКНФ аналогичны методам получения МДНФ и поэтому сформулируем лишь правила получения МКНФ:

1. Представить ФАЛ в СКНФ. Если она задана таблицей, то произвести запись функции по нулям, как это было сформулировано ранее. Если дана СДНФ, то из нее легко получить СКНФ:

   ,

    

   т.е. нужно функцию представить в виде конъюнкции недостающего числа дизъюктивных членов с соответсвенно расставлеными отрицаниями.

    
2. При задании функции в произвольной конъюктивной форме, применяя

   формулы развертывания:

    

   

    

   . . . . . . . . . . . .,

    

   получить СКНФ.

    
3. Выполнить все операции неполного склеивания:

   

    

   и поглощения: 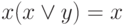, получить сокращенную КНФ.

    
4. Применить любой из методов минимизации: испытание членов, диаграммы Вейча, метод импликантных матриц.
   • При выполнении метода испытания членов необходимо каждый конъюктивный член приравнять нулю. Найти значения аргументов, которые обращают его в нуль, удалить его из выражения функции и найти значение функции при найденных значениях аргументов. Если функция обратится в нуль, то конъюктивный член является лишним.

     По возможности отбросить одновременно несколько членов, поступить как и при минимизации функции ДНФ.

      
   • При использовании диаграмм Вейча ищутся правильные конфигурации, образованные нулями.
   • При применении метода импликантных матриц поступают как и в случае ДНФ, только колонкам присваивают имена конституент" 0 " функции, записанной в СКНФ, а горизонтальным рядам – простых импликант. Далее ищут оптимальное покрытие.

Выводы из данной статьи про минимизация неполностью определенных функций указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое минимизация неполностью определенных функций и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.