Системы исчисления. Виды. Методика выбора и преобразования

Привет, Вы узнаете о том , что такое системы исчисления, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое системы исчисления, преобразование систем исчисления , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

План

• Основные определения:
• Классификация систем исчисления и история
• Системы счисления, используемые в компьютере
• Применение позиционной системы исчисления
• Выбор системы счисления.
• Перевод чисел из одной системы счисления в другую.

Расссмотрим способы представления чисел в ЭВМ, методы выполнения арифметических операций, которые отличны от методов, получивших широкое распространение на практике.

Основные определения:

Как известно, еще в 19 веке производство операций над числами, содержащими много разрядов, представлялось сложной задачей, решить которую могли только профессионалы. В это время были уже разработаны основные правила выполнения операций над многозначными числами узбекским математиком Аль-Хорезми. Общие закономерности, по которым строились эти правила, впоследствии получили название АЛГОРИТМА. Они настолько широко вошли в жизнь, что, производя эти операции над многозначными числами, мы не задумываемся над тем, что выполняем строгую систему правил.

Способ представления изображения произвольных чисел с помощью некоторого конечного множества символов назовем системой счисления .

В повседневной практике мы пользуемся, как правило, десятичной системой счисления. Ответ на вопрос: " Почему именно эта система счета получила наибольшее распространение? " - сейчас дать затруднительно. В литературе, как правило, в качестве обоснования приводится тот факт, что на руках человека - в сумме 10 пальцев. Вряд ли это обоснование можно принимать всерьез. На практике мы сталкиваемся и с более сложными, в частности, со смешанными системами. Например, система счета времени, где за единицу принята секунда, минута, час, сутки, неделя, месяц, год.

Или система счета денег, до недавнего времени применявшаяся в Англии (пенс, шиллинг, фунт):

12п = 1ш, 20ш = 1ф.

Или еще более интересная - римская система счета, которая использует символы: I - 1, V - 5, X - 10, L - 50, C - 100, D - 500, M - 1000.

Эта система является особой и применяется редко (циферблат, архитектура, история и т.д.)

Система счисления - строго определенная совокупность приемов и правил для наименования и отображения чисел с помощью набора символов, которые называются цифрами.
Цифры - знаки, используемые при записи чисел.
Числа и цифры различаются между собой так же, как различаются между собой слова и буквы.
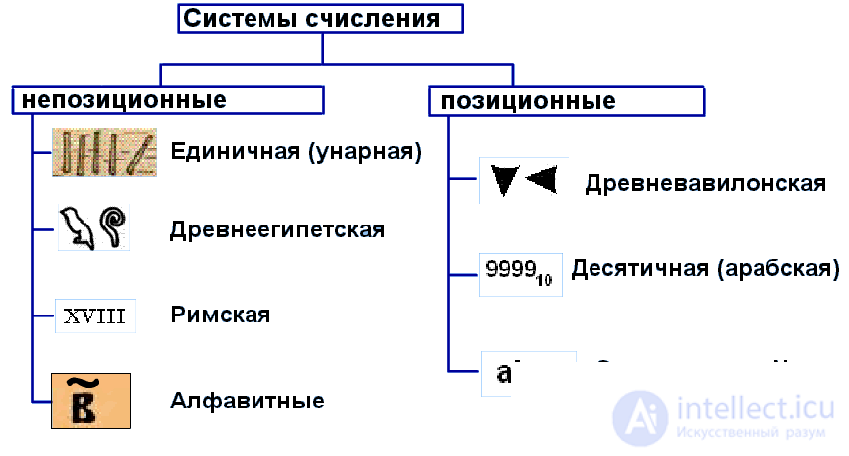
Основные виды систем счисления:
- Унарная (числа отображаются засечками, черточками, палочками и т.д.);
- Непозиционная (от положения цифры в записи не зависит величина, которую она означает);
- Позиционная (величина, обозначаемая цифрой в записи числа, зависит от ее позиции в этой записи)

-символическая
Позиция - место цифры в числе.

Классификация систем исчисления и история

Примеры непозиционных систем счисления:

• древнеегипетская;
• римская (I = 1; V = 5, X = 10; L = 50; D = 500; M = 1000);
• алфавитная.

Примеры позиционных систем счисления:

• вавилонская (шестидесятеричная);
• пятеричная;
• двенадцатеричная;
• двадцатеричная;
• с ступенчатой весом разрядов (десятичная, шестнадцатеричная, восьмеричная, троичная, двоичная).

УНАРНЫЕ СИСТЕМЫ

В унарных системах счисления число образуется путем повторения одного знака, символизирующего единицу.
Способ записи: зарубки, черточки, палочки

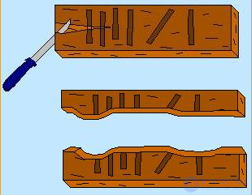
Археологами найдены такие "записи" при раскопках культурных слоев, относящихся к периоду палеолита
(10 - 11 тыс. лет до н. э.)

Этот способ записи чисел называют единичной ("палочной”, “унарной”) системой счисления .

Единичная запись для таких чисел была громоздкой и неудобной, поэтому люди стали искать более компактные способы обозначать большие числа.

Непозиционные системы

В таких системах счисления от положения знака в записи числа не зависит величина, которую он обозначает.

Египетская нумерация Была создана 5000 лет тому назад

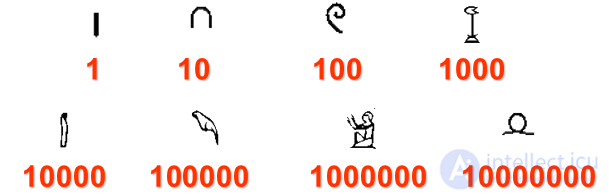
1		Как и большинство людей для счета небольшого количества предметов Египтяне использовали палочки Каждая единица изображалась отдельной палочкой
10		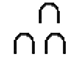Такими путами египтяне связывали коров Если нужно изобразить несколько десятков, то иероглиф повторяли нужное количество раз. Тоже самое относится и к остальным иероглифам.
100		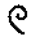Это мерная веревка, которой измеряли земельные участки после разлива Нила
1000		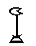Цветок лотоса
10000		Поднятый палец - будь внимателен
100000		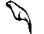головастик
1 000 000		Увидев такое число, обычный человек очень удивится и возденет руки к небу
10000000		Египтяне поклонялись богу Ра, богу Солнца и, наверное, так изображали самое большое свое число

Число 1 245 386
в древнеегипетской записи будет выглядеть

Алфавитная нумерация

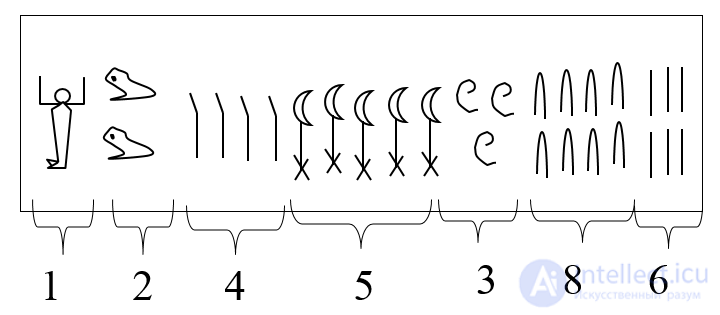
В середине V в. до н. э. появилась запись чисел нового типа, так называемая алфавитная нумерация.

В этой системе записи числа обозначались при помощи букв алфавита., над которыми ставились черточки: первые девять букв обозначали числа от 1 до 9, следующие девять - числа 10, 20, 30, ..., 90, и следующие девять - числа 100, 200, ..., 900.
Таким образом, можно было обозначать любое число до 999

Древнегреческая нумерация

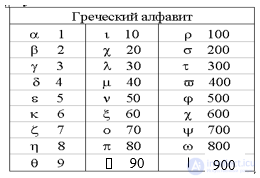
Запись алфавитными символами могла делаться в любом порядке, так как число получалось как сумма значений отдельных букв.

Например, записи – 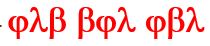все эквивалентны и означают число 532.
Однако выполнять арифметические вычисления в такой системе было настолько трудно, что без применения каких-то приспособлений оказалось обойтись практически невозможно

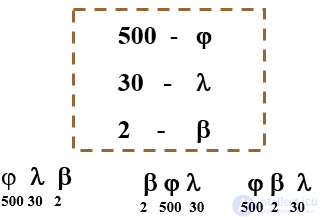
Славянская кириллическая нумерация

Чтобы различать буквы и цифры, над числами ставился особый значок — титло ( ~ ).

Так можно было записывать числа до 999. Для больших чисел использовался знак тысяч , который ставился впереди символа, обозначавшего число

До XVII века эта форма записи чисел была официальной на территории России, Белоруссии, Украины, Болгарии, Венгрии, Сербии и Хорватии. До сих пор православные церковные книги используют эту нумерацию.

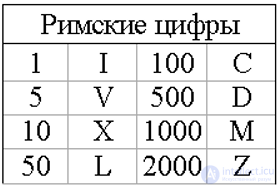
Римская нумерация

Это нумерация, известная нам и в настоящее время. С нею мы достаточно часто сталкиваемся в повседневной жизни.

Это номера глав в книгах, указание века, числа на циферблате часов, и т. д. Возникла эта нумерация в древнем Риме. В ней имеются узловые числа: один, пять и т. д.
Остальные числа получались путем прибавления или вычитания одних узловых чисел из других

Например,
четыре записывается как IV, т. е. пять минус один,
восемь — VIII (пять плюс три), сорок—XL (пятьдесят минус десять),
девяносто шесть—XCVI (сто минус десять плюс пять и плюс еще один) и т. д.

Символическая система исчисления

Рассмотрим подробнее символическую систему исчислени. В этих системах каждому числу ставится в соответствие свой символ. Эти системы не находят широкого применения в силу естественной их ограниченности (алхимия, кодированные сообщения) -бесчисленного множества символов, которое требуется для изображения всех возможных чисел. Поэтому эти системы из рассмотрения опустим.

Позиционные системы счисления.

Само название этих систем указывает на связь значимости числа и его изображения от позиции.Название системы зависит от количества используемых в ней знаков.

Позиционные системы - системы счисления, в которых вклад каждого знака в величину числа зависит от его положения (позиции) в последовательности знаков, изображающей число

Позиция - некоторое место, в котором может быть представлен лишь один символ.

• Вавилонская
• Десятичная
• Двоичная
• Восьмеричная
• Двенадцатеричная
• и др.

Вавилонская система счисления 2500-2000 лет до н.э.

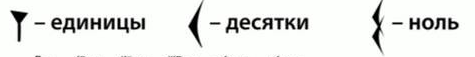
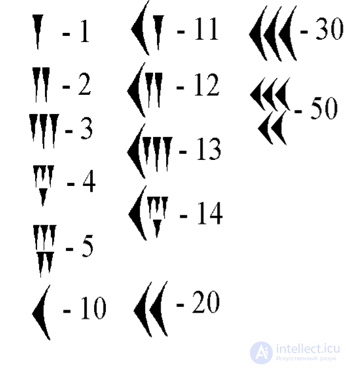
Рассмотрим десятичную систему.

Цифры 1234567890 возникли в Индии около 400 г. н. э.

Арабы стали пользоваться подобной нумерацией около 800 г. н. э.

Примерно в 1200 г. н. э. эту нумерацию начали применять в Европе

Из арабского языка заимствовано и слово "цифра"
(по-арабски "сыфр"), означающее буквально "пустое место"
Это слово применялось для названия знака пустого разряда, и этот смысл сохраняло до XVIII века, хотя еще в XV веке появился латинский термин "нуль" (nullum - ничто). Форма индийских цифр претерпевала многообразные изменения.

Та форма, которой мы сейчас пользуемся установилась в XVI веке.

1 2 3 4 5 6 7 8 9 0

По мнению марроканского историка Абделькари Боунжира арабским цифрам в их первоначальном варианте было придано значение в строгом соответствии с числом углов, которые образуют фигуры

В древней Индии и Китае существовали системы записи, построенные на
МУЛЬТИПЛИКАТИВНОМ ПРИНЦИПЕ. Об этом говорит сайт https://intellect.icu . В таких системах для записи одинакового числа единиц, десятков,сотен или тысяч применяются одни и те же символы, но после каждого символа пишется название соответствующего разряда.

Если десятки обозначить символом Д, а сотни - С, то число 325 будет выглядеть так : 3С2Д5.

Между II и VI вв.н.э. Индийцы познакомились с греческой астрономией.

Индийцы и соединили греческие принципы нумерации со своей десятичной мультипликативной системой.

Десятичная система является позиционной потому, что величина, обозначаемая цифрой в записи числа, зависит от ее позиции

Например

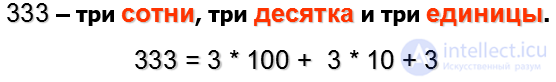
Всякое десятичное число можно представить как сумму произведений составляющих его цифр на соответствующие степени десятки:

Число 10 является основанием десятичной системы счисления.

Официальное рождение двоичной арифметики связанно с именем Г.В. Лейбница, опубликовавшего в 1703 г. статью, в которой он рассмотрел правила выполнения арифметических действий над двоичными числами.Двоичная система проста, так как для представления информации в ней используются всего два состояния или две цифры.
Такое представление информации принято называть двоичным кодированием. Представление информации в двоичной системе использовалось человеком с давних времен. Так, жители островов Полинезии передавали необходимую информацию при помощи барабанов: чередование звонких и глухих ударов.

В этой десятичной системе число представляется в виде полинома " n " степени, а изображается совокупностью некоторых символов, каждый из которых имеет различный вес в зависимости от позиции, которую он занимает.

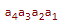- число; 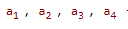- символы.

Всем позициям приписывается различный вес, который чаще всего выбирается как целая степень основания системы.

Основание системы счисления - число, которое является мощностью множества различных символов, допустимых в каждой позиции числа.

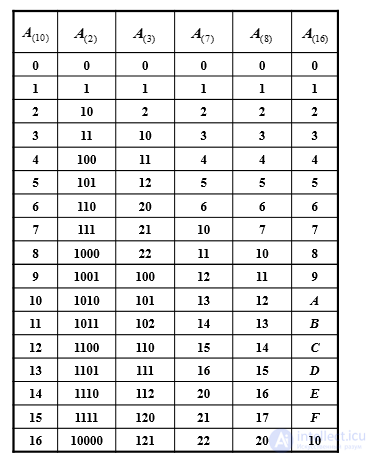
Так для десятичной системы допускаемыми являются символы: 0, 1, 2, 3,..., 9.

Обозначим через " p " основание системы счисления. Тогда веса позиций числа могут быть представлены так:

Само число, изображение которого имеет вид, например, 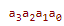может быть представлено так:

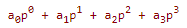- это развернутая запись числа в позиционной системе.

Например:

В отличие от системы счета времени, десятичная система является однородной, т.е. одних и тех же десятичных символов достаточно, чтобы изобразить любое число. В то время как в смешанных системах нужно придумывать все новые и новые символы для того, чтобы изобразить следующее по величине число.

Таким образом, однородность - одно из важных свойств позиционных систем.

Двенадцатеричная система счисления

Основание системы равно двенадцати. Используются десять цифр от 0 до 9 и две латинские буквы А и В.

Применение:

• Считали фаланги пальцев
• Для счета использовали большой палец
• Число 12 – дюжина
• В сутках две дюжины часов Час делится на пять дюжин минут
• Столовые сервизы на 6 или 12 персон
• Набор карандашей или фломастеров из 6 или 12 цветов.

Системы счисления, используемые в компьютере

Двоичная система счисления

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в компьютерах двоичная система счисления

Алфавит двоичной системы счисления состоит из 0 и 1

Основанием, служит цифра 2

Достоинства двоичной системы :

• Простота кодирования;
• Простота арифметических действий;
• Простота записи, хранения и передачи техническими средствами.

Недостатки двоичной системы:

• Много места занимает запись числа;
• Трудоемкость перевода в 10 с/с и наоборот.

Восьмеричная система счисления

Всякое восьмеричное число можно представить как сумму произведений составляющих его цифр на соответствующие степени восьмерки:

Алфавит:
0, 1, 2, 3, 4, 5, 6, 7

Основанием является цифра 8 Например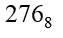

Шестнадцатеричная система счисления

Всякое шестнадцатеричное число можно представить как сумму произведений составляющих его знаков на соответствующие степени числа шестнадцать:

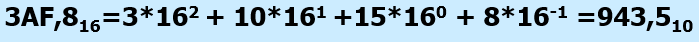
Алфавит:0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

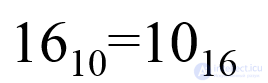
Основанием является цифра 16

Применяется для целей коммуникации человека с ЭВМ. например просмотр байт кода

Почему в компьютерах используются также восьмеричная и шестнадцатеричная системы счисления?
Двоичная система, удобная для компьютеров, для человека неудобна из-за ее громоздкости и непривычной записи.
Перевод чисел из десятичной системы в двоичную и наоборот выполняет машина.
Для программистов удобнее работать с более компактной записью.
Такими системами и являются 8-ая и 16-ая

Применение позиционной системы исчисления

Любое число X в позиционной системе счисления можно представить в виде:

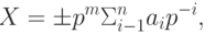
где

m - число позиций или разрядов, отведенное для изображения целой части числа.

n - общее число разрядов в числе.

ai - любой допустимый символ в разряде, т.е. ai = {0, 1, 2,..., p-1}.

p - основание системы счисления.

Например:

1. Заметим, что число, равное основанию системы счисления, т.е. " p ", в самой системе с основанием " p " записывается только в двух позициях ( разрядах ), а именно так:

2. Заметим также, что разделение числа на две части - дробную и целую - имеет смысл лишь в позиционных системах.
3. Заметим, что основание системы для представления числа мы можем выбрать произвольное. Такой же произвол мы можем допустить и в назначении весов разрядов. Однако наиболее целесообразно считать его, как и в десятичной системе, естественным, т.е. ввести в качестве степеней основания числа натурального ряда:

   

Выбор системы счисления.

Возникает естественный вопрос, является ли общепринятая система счисления с основанием 10 оптимальной? Если да, то с каких позиций? Вопрос заслуживает внимания, т.к. одна из первых ВМ (ENIAC) использовала именно десятеричную систему.​

Прямой и однозначный ответ на этот вопрос невозможен. Можно дать много различных ответов и все они будут справедливы лишь для каких-то определенных условий.

Введя общее представление числа в позиционной системе, мы усомнились в достоинствах десятеричной не потому, что она вдруг проявила свои отрицательные качества, а потому что ее преимущества явны лишь при ручных методах счета. Нас же интересуют, прежде всего, такиесистемы счисления, которые будут удобны и экономичны при автоматических вычислениях с помощью ЭВМ. Мы должны также помнить, что необходимо для этого иметь саму ЭВМ.

Покажем, что десятеричная система не устарела. Например, для производства экономичных расчетов обычно приходится иметь дело с очень большими объемами числовой информации. Тогда с введением новой системы пришлось бы воспользоваться следующей цепочкой действий:

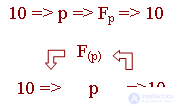
Т.е. нужно было бы из десятеричной системы перевести информацию в " p "-систему, произвести над ней необходимые операции всистеме " p ", затем снова сделать, но обратный перевод из " p "-системы в десятеричную, т.к. отказ от десятеричной системыпотребовал бы и устранения первого этапа.

Если преобразование из десятеричной системы в " p "-систему требует не слишком много времени, в то же время, если выполнение функции F будет в системе " p " сделано много быстрее, то тогда эта цепочка действий будет оправданной.

Но для экономической информации характерно то, что очень несложные операции нужно производить всякий раз над большим объемом исходных данных. Так что в данном случае вряд ли целесообразно переходить к новой системе. Это и является объяснением того факта, что в настоящее время значительное число ЭВМ строится именно в десятеричной системе счисления.

Однако ЭВМ предназначены не только для выполнения экономических расчетов. В большинстве случаев неэкономических применений ЭВМ имеют дело с задачами, в которых общий объем исходных данных невелик, но общее число необходимых операций огромно. Именно для такого рода применений рассмотренная последовательность действий может оказаться выгодной.

Очевидно, что можно, не сужая области применения ЭВМ, задаться величиной некоторого самого большого числа. Пусть это будет числоM. Воспользуемся позиционной системой счисления с основанием " p ", и тогда потребуется " n " разрядов, чтобы представить все Mчисел:

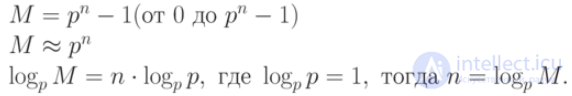
Оборудование, которое нужно для хранения любого числа от 0 до M пропорционально произведению основания системы счисления на количество разрядов.

Таким образом, при заданном числе M количество цифроразрядов при основании " p ":

где:

цифроразряд - эквивалент оборудования,

p*n - число устойчивых состояний элемента памяти,

n - число разрядов в числе.

Рассмотрим пример:

Пусть есть 24 цифроразряда.

Количество цифроразрядов говорит как о величине оборудования, так является характеристикой быстродействия. Как увидим позже, в позиционной системе счисления времена выполнения операций могут быть выражены через количество разрядов в числе.

Считаем " p " - величиной непрерывной. Находим производную от (6.1) по величине " p ". Берем вторую производную по " p ". Увидим, что первая производная обращается в нуль, а вторая - больше нуля при p = e. Т.е. получаем минимум при p = e.

Таким образом, оптимальной по оборудованию и быстродействию является система с основанием е.

Но е = 2,718...

Поэтому оптимальной является система с основанием р = 3.

Построим функцию, характеризующую отношение оборудования в системе с основанием " p " относительно системы с основанием " 2 ".

Т.е. 10-я система является более чем в 1,5 раза неэкономичной по отношению ко 2-ой системе, а 3-я система оказывается лишь на 5% экономичнее 2 й.

Действительное обоснование экономичности той или иной системы выглядит несколько сложнее.

Когда говорим об экономичности, то, прежде всего, имеем ввиду объем оборудования, сосредоточенный в АУ и ЗУ. Объем оборудования УУ не находится в столь простой зависимости от " p " да и в АУ учитывается лишь оборудование, связанное с элементами хранения информации, но не логическое оборудование.

Более детальный анализ показывает, что наиболее эффективными являются системы с основанием, кратным 2, т.е. 2, 4, 8, 16. Специфика построения схем ЭВМ показывает, что наиболее эффективной является 16-ая система. Именно она и применяется в современных машинах.

Мы же будем считать эффективной систему с основанием 2 по причине ее наибольшего распространения.

Вот основные соображения в пользу этой системы:

1. Высокая информационная эффективность.
2. Простота и надежность работы 2-ого элемента хранения информации (т.е. имеющего 2 устойчивых состояния)
3. Совпадение максимального числа состояний элемента с максимальным числом значений двоичной переменной, дающее возможность не строить специальные устройства для выполнения логических операций.
4. Простота построения схем для выполнения простых операций.
5. Более высокая скорость выполнения основных арифметических операций.

Последнее требует специального пояснения. В данном случае рассматриваются не отрезки времени, необходимые для выполнения тех или иных операций, а скорость, определяемая косвенно по относительному числу операций, которые требуется провести для выполнения, например, деления или умножения в двоичной или прочих системах.

Если " p " - основание системы счисления, то максимальная цифра в одном разряде - (p-1).

Если N - максимальное число, то для его изображения требуется logpN разрядов.

Для того чтобы выполнить операцию умножения, например, потребуется (p-1)*logpN операций сложения. Если сравнить это число операций в системе с основанием " p " и отнести его к числу операций в системе с основанием " 2 ", то может получиться следующаяфункция:

Это лишь основные соображения в пользу выбора в качестве основы двоичную систему счисления. Существуют и другие (контроль,диагностика неисправностей), но мы их из рассмотрения опустим.

Перевод чисел из одной системы счисления в другую.

Всякий раз, когда используется для вычислений система счисления, отличная от фактической, необходимо выполнить перевод 10 => p, p => 10.

Основные методы перевода чисел:

• метод перевода чисел с основанием, кратным 2n;
• метод замещения;
• метод деления (умножения) на основу;,
• метод вычитания степеней.

Есть системы, дающие значительно более высокие скорости, но и требующие большего количества оборудования.

Этот перевод может быть выполнен:

1. вручную,
2. на ЭВМ (с помощью специальных программ).

Во всех этих случаях принципиально используется различные подход и методы. В связи с тем, что нам придется готовить информацию для программы вручную, мы рассмотрим, прежде всего, методы, направленные на ручной перевод.

Итак, имеем дело с позиционной системой счисления с основанием " p ", с естественными весами разрядов.

В качестве промежуточной используется, естественно, десятичная система. Вначале число переводится из системы " p " в 10-ую, затем из 10-ой в систему с нужным основанием.

Мы отступим от этого правила и воспользуемся алгоритмом непосредственного перевода из системы с основанием " p " в систему соснованием " q ".

Обычно произвольное число, содержащее целую и дробную части, переводят по частям: вначале целую, затем дробную часть.

Рассмотрим перевод целых чисел:

Перевод осуществляется по следующему правилу: исходное число, записанное в системе с основанием " p " и его частные последовательно делятся на число " q ", представленное в системе " p ". Деление производится в системе с основанием " p " и продолжается до получения результата, меньшего " q ". Первый остаток, меньший " q ", дает старшую цифру числа Nq. Остатки от деления дают остальные цифры числа Nq.

Пример:

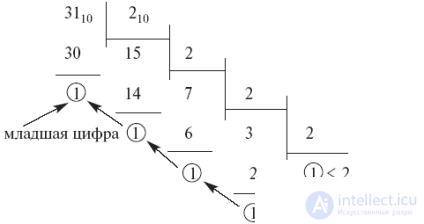
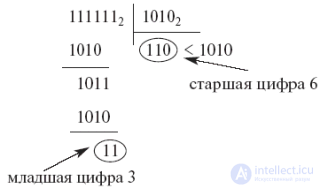
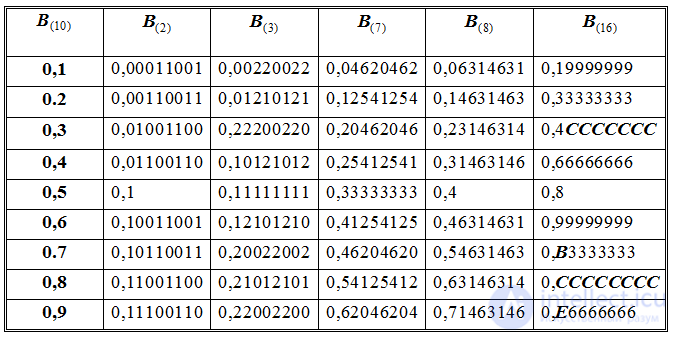
Перевод дробных чисел из системы с основанием " p " в систему с основанием " q " выполняется по следующему правилу: исходное число Dp последовательно умножается на число " q ", записанное в системе " p ". Целые части получаемых произведений дают " p "-ые записи " q "-х цифр, начиная со старшей. Умножение производится в системе с основанием " p " до получения необходимой точности.

Пример:

1. 

2. 

3. 

   Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.

   Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для другихсистем. Допустим, что имеется некоторое целое число N8 в 8-ой системе. Оно может быть представлено в виде:

   

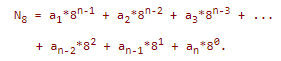
   Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.:

   

4. 

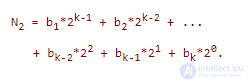
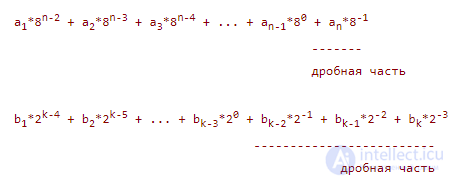
   Так как числа были равны, то получается одинаковые частные и одинаковые остатки:

5. 

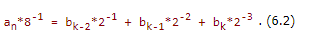
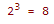   Если снова разделим целые части на , то опять получим равные частные и равные остатки.

   При этом видим, что каждой восьмеричной цифре соответствует ее двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы ее двоичным эквивалентом и обратно.

   Пример:

   

6. Аналогично для 4-ой системы:

    
   Аналогично для 16-ой системы:
   

   

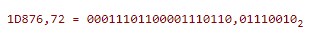
   Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись.
   

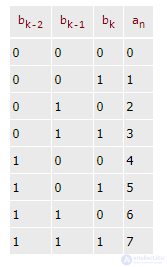
   Если умножить последние соотношения (6.2) на 8, то:

   

1 МЕТОД ПЕРЕВОДА ЧИСЕЛ С ОСНОВАНИЕМ, КРАТНЫМ 2n

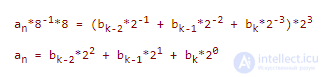
Для того, чтобы целое двоичное число записать в системе счисления с основанием , необходимо данное двоичное число разбить справа налево на группы по n цифр в каждой. Если при этом в последний левой группе окажутся меньше n разрядов, то необходимо дополнить ее нулями до нужного числа разрядов. Затем следует рассмотреть каждую группу как n-разрядное двоичное число и заменить ее соответствующей цифрой в системе .

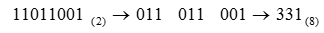
Для перевода дробных частей двоичных чисел в восьмеричную или шестнадцатеричную системы аналогичное разбиение на двоичные триады или тетрады производится от запятой вправо (с дополнением недостающих последних цифр нулями).

2 МЕТОД ЗАМЕЩЕНИЯ

Чаще всего используется для перевода чисел из недесятичных системы счисления в десятичную.

Примеры:

3а метод деления (умножения) на основу

Чтобы перевести целую часть числа из системы с основанием p в систему с основанием q, необходимо разделить эту часть числа на q. Остаток от деления даст младший разряд числа в системе q. Полученную при этом долю необходимо снова разделить на q - остаток даст следующий разряд числа и т.д.

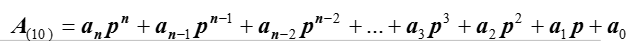
Для определения разделим А(10) на р . После деления получим частицу:



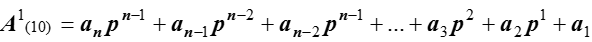
и остаток от деления .

Перевод чисел методом деления на основу

3б Перевод чисел методом деления на основу

Для перевода дробной части, ее необходимо умножить на q. Целая часть полученного произведения будет первым (после запятой, отделяющей целую часть от дробной) знаком в системе с основанием q. После отделения дробной части произведения, ее необходимо снова умножить на q. Целая часть полученного числа будет следующим знаком и т.д.

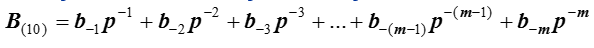
Для того, чтобы определить первую цифру после запятой в новом представлении числа умножим на р. После умножения получим

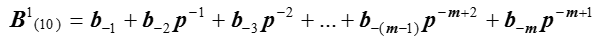
Целая часть произведения дает значение .

3б Перевод чисел методом умножения на основу

4 метод вычитания степеней

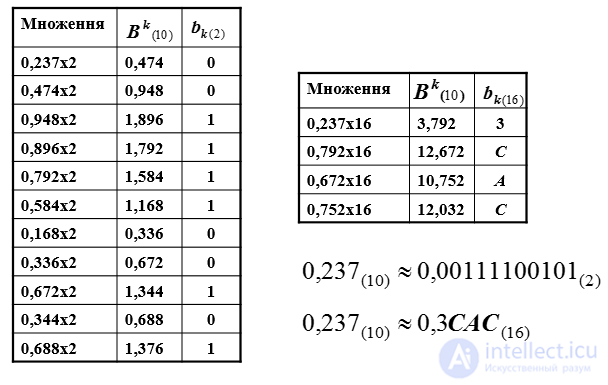
Из исходного числа с основанием р последовательно вычитается максимально допустимая степень числа с основанием q, умноженной на максимально возможный коэффициент, меньший основания q (например, для двоичной системы таким коэффициентом будет 1).

Этот коэффициент и является значимой цифрой числа в новой системе.

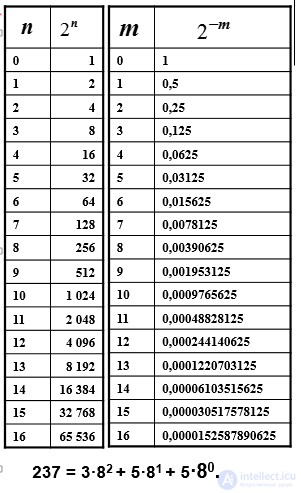
Пример (p = 10, q = 2)

Таким образом, можно записать ступенчатый ряд:

Контрольные вопросы и задания для самопроверки

1. Что понимается под системой счисления?
2. В чем заключаются различия между позиционной и непозиционной системами счисления?
3. Какие системы счисления могут быть отнесены к непозиционных?
4. Каким образом записываются числа в римской системе счисления?
5. Какие преимущества и недостатки десятичной, восьмеричной, шестнадцатеричной и двоичной систем счисления?
6. Какая система счисления является наиболее экономной при представлении чисел и какая система счисления является наиболее удобной для использования в компьютерных системах и почему?
7. Почему на практике почти не находят применения системы счисления с основанием более 16?
8. Составьте таблицу, в которой перечислены все двоичные, троечные, восьмеричные и шестнадцатеричные числа от 0 до 32.
9. Как определяется количество двоичных разрядов, необходимых для кодирования одной цифры произвольной позиционной системы счисления?
10. Выучите наизусть запись всех двоичных чисел от 0 до 32.

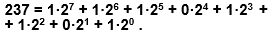
Выводы из данной статьи про системы исчисления указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое системы исчисления, преобразование систем исчисления и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.