3: Совершенные дизъюнктивные и конъюнктивные нормальные формы ФАЛ

Привет, Вы узнаете о том , что такое совершенные дизъюнктивные, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое совершенные дизъюнктивные, конъюнктивные нормальные формы фал , настоятельно рекомендую прочитать все из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ.

Аннотация: В лекции дано определение совершенной дизъюнктивной и конъюнктивной нормальных форм. Представлены правила записи функции по нулям и единицам. Дано понятие функциональной полноты, поставлена задача минимизации функции. Сформулирована теорема Квайна.

Введем понятие степени:

Рассмотрим конъюнкцию вида:

Существует 2ⁿ наборов вида  Поставим в соответствие каждой конъюнкции (*) номер набора i и образуем дизъюнкцию всех конъюнкций:

Теорема (без доказательства):

Любая ФАЛ, зависящая от ' n ' аргументов, может быть представлена в форме:

Из этой теоремы вытекает ряд важных следствий:

1. Она дает возможность перейти от табличного задания функции к аналитической форме и сделать обратный переход.
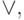
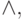2. Устанавливает так называемую функциональную полноту связок (базиса) "   -", т.к. позволит построить в этом базисе произвольную ФАЛ от произвольного числа аргументов.

Примечание:

1. Если  то соответствующая форма функции называется дизъюнктивной нормальной (ДНФ).
2. Если i=n, то каноническая форма функции носит название совершенной ДНФ (СДНФ). Дизъюнкции берутся по тем наборам, на которых функция f(X_{1},X_{2},...,X_{n})=1

Пример: ДНФ

Пример: СДНФ

В ДНФ в каждый член любая переменная входит в прямом виде или с отрицанием.

Аналогичная теорема справедлива и для представления функции в конъюнктивной нормальной форме (КНФ):

или при представлении в совершенной КНФ (СКНФ):

где: & означает, что конъюнкции берутся по тем наборам, на которых

f(Х_{1}, Х_{2}, ... Х_{n})=0.

Дадим на основании этих теорем правило перехода от табличной формы функции к СДНФ и СКНФ.

Переход от табличной формы функции к СДНФ или правило записи функции по единицам:

1. Выбрать те наборы аргументов, на которых f(Х_{1}, Х_{2}, ... Х_{n})=1.
2. Выписать все конъюнкции для этих наборов. Если при этом Х_{i} имеет значение ' 1 ', то этот множитель пишется в прямом виде, если ' 0 ', то с отрицанием.
3. Все конъюнктивные члены соединить знаком дизъюнкции 

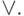
Пример:

Правило перехода от табличной формы задания функции к СКНФ или правило записи функции по нулям.

1. Выбрать те наборы аргументов, на которых f(Х_{1}, Х_{2}, ... Х_{n})=0.
2. Если при этом Х_{i} имеет значение ' 0 ', то остается без изменений. Если ' 1 ', то с отрицанием.
3. Все дизъюнктивные члены соединить знаком конъюнкции 

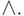
Пример:

Пример:

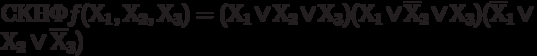
Рассмотрим способ получения СДНФ из СКНФ и обратно.

Из таблицы 2.1 с помощью способа записи функции по нулям следует, что СКНФ той же функции дизъюнкции будет иметь вид:

Итак, имеем две формы одной и той же функции:

Итак, видно, что общее число членов в этих двух формах равно сумме нулей и единиц функции, то есть равно 2ⁿ.

Если в исходной форме функции, записанной в СКНФ или СДНФ, содержится z членов, то в другой ее форме (т.е. СДНФ или СКНФ ) их будет (2ⁿ- z).

Поскольку в функцию мы включаем дизъюнктивные или конъюнктивные члены и берем их по наборам, на которых функция или обращается в ' 0 ', или в ' 1 ', то для перехода от одной формы задания функции к другой нужно выписать все недостающие члены и поставить над каждой переменной отрицание, а также заменить знаки конъюнкции на дизъюнкцию и обратно.

т.е. Об этом говорит сайт https://intellect.icu . получили СДНФ.

Практический смысл перехода заключается в том, что можно определить, реализация какой формы потребует меньший объем оборудования.

Понятие функциональной полноты ФАЛ

Было отмечено, что техническая (физическая) задача синтеза произвольного устройства сводится к математической задаче построения произвольной ФАЛ.

Естественно возникает вопрос, какое количество связок необходимо, чтобы построить произвольную ФАЛ. Ответ на этот вопрос не однозначен. Мы видим, что, например, с помощью только функции f_{0} (константа 0 ), f_{15} (константа 1 ) произвольную ФАЛ построить нельзя. Нельзя ее построить и с помощью только инвертора. Существуют и другие базисы: 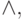  1, |. Есть такжеодноэлементные базисы: f_{8} – стрелка Пирса, f_{14} – штрих Шеффера, И-НЕ, ИЛИ-НЕ.

Технически синтез устройства означает, что нужно иметь некоторый набор элементов, ФАЛ которых образуют базис, чтобы можно было построить реальное устройство.

Однако, как было отмечено, задача синтеза ФАЛ – идеальная модель. В действительности, для построения реальных устройств пользуются несколько более расширенным набором элементов - усиления и коррекции сигналов.

Минимизация ФАЛ и ограничения при ее рассмотрении

Покажем на примере, что СДНФ не является экономной формой записи:

на основании полного склеивания по Х_{2} мы видим, что запись стала короче, т.к. содержит меньшее число связок и букв. Физически это означает, что устройство, которое реализует эквивалентную, но более простую функцию, будет иметь в своем составе меньшее количество оборудования, а следовательно, будет работать надежнее.

Итак, задача синтеза устройства должна быть дополнена задачей уменьшения оборудования в нем. С математической точки зрения это задача построения минимальной ФАЛ.

Под минимальной ФАЛ понимается такая форма, в которой содержится меньшее количество букв и членов, чем в ее исходной форме.

Речь идет именно о буквах, а не о переменных, так в функции:

 имеется 6 букв и только 2 переменных.

Видно, что если какое-либо элементарное произведение входит в функцию, то при добавлении к нему новых сомножителей, полученное произведение так же будет входить в функцию.

Пример: если Х_{1}Х_{2} входит в функцию от любого числа аргументов ( >2 ), то в нее войдет, например, произведение Х_{1}Х_{2}Х_{3}.

Это можно показать так:

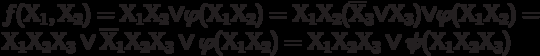
Дадим ряд определений:

1. Произведение одной или нескольких неповторяющихся переменных, взятых с отрицанием или без него, называют элементарным.

   Например, Х_{1} Х_{2} Х_{3} – элементарное произведение, т.к. в него входят различные буквы Х_{1} Х_{2} Х_{3}.

    
2. Дизъюнкция элементарных произведений – ДНФ.
3. ДНФ является минимальной, если в ней минимальное число букв и членов.
4.  Конституентой единицы функции называют функцию, принимающую значение единицы только на одном наборе аргументов.

   Обычно конституенты единицы выражают через произведение всех переменных, от которых зависит функция. СДНФ – дизъюнкцияконституент единицы.

    
5.  Ранг произведения – число букв, входящих в него.
6. Собственной частью называется произведение, полученное путем отбрасывания одной или нескольких переменных.

   Например, Х_{1} Х_{2} Х_{3} Х_{4}, где Х_{1}, Х_{1} Х_{2}, Х_{1} Х_{2} Х_{3} – некоторые собственные части.

    
7. Если функция  равна нулю на наборах аргументов, на которых обращается в нуль функция F, то говорят, что  являетсяимпликантой функции F (т.е. нулей у импликанты не меньше, чем у функции).
8. Простой импликантой называется произведение, которое само входит в выражение функции, но никакая его собственная часть в выражение функции не входит.

   Например, : здесь Х_{1} - простая импликанта, а Х_{1} Х_{2} Х_{3} и Х_{1} Х_{3} - не простые.

    

Понятие покрытия

Определение. Если на каком-либо наборе f принимает значение а_{1}, а  – значение а_{2}, то говорят, что f своим значениема_{1} покрывает значение а_{2} функции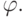 

При минимизации ФАЛ стремятся получить форму, в которой будет меньше букв, чем в исходной. По отношению к ДНФ эта форма называется сокращенной (Сок. ДНФ).

Смысл построения Сок. ДНФ заключается в том, что в нее входят такие элементарные произведения, которые своими единицами покрывают не одну единицу исходной функции, а несколько.

Так, каждое элементарное произведение, входящее в СДНФ, покрывает только одну единицу функции.

Например:

1      1       1

Эти единицы функции могут быть накрыты более короткими произведениями: Х_{1} накрывает две единицы:  и  и , которое накрывает также две единицы:  и , т.е.

ТЕОРЕМА (без док-ва):

Любая ФАЛ может быть представлена единственным образом в Сок. ДНФ, т.е. записана в виде дизъюнкции простых импликант.

Сокращенная форма не означает, что эта форма является минимальной. Однако для практической реализации эта форма более удобна, чем совершенная.

Рассмотрим метод получения Сок. ДНФ, предложенный Квайном. Этот метод, и, в частности, теорема Квайна в явном и неявном виде входит практически во все методы минимизации.

Исходная форма функции – совершенная ДНФ.

ТЕОРЕМА Квайна:

Если в СДНФ в начале произвести все операции неполного склеивания, а затем все операции поглощения, то в результате получитсясокращенная ДНФ.

Покажем, что, применяя операцию неполного склеивания, получим все простые импликанты функции. Введем операцию развертывания, которая обратна операции склеивания: это есть умножение каждого произведения на выражение вида 

Пусть  – простая импликанта некоторой  трех переменных. Тогда:

получатся после многократного применения этой операции дизъюнкции конституент единицы исходной функции, т.е. ее СДНФ.

В эту форму, вообще говоря, могут входить несколько одинаковых членов, т.к. разные простые импликанты могут дать одинаковыеконституенты единицы. Поэтому, отбросив в ДНФ лишние члены, получим ее СДНФ.

По отношению к СДНФ применяется операция неполного склеивания, т.к. одно и то же произведение, вообще говоря, может склеиваться с несколькими другими, давая различные импликанты, то чтобы не лишиться возможности провести все операции склеивания, приходится каждое произведение, которое участвовало в операции склеивания, оставить для других операций.

Пример:

Таким образом после выполнения операции неполного склеивания получится не только дизъюнкция простых импликант, но и частьконституент единицы.

Если теперь провести все операции поглощения, то в полученной форме функции f останутся только простые импликанты. Покажем это. Пусть в результате операций склеивания получится член x, не являющийся простой импликантой.

Тогда x=y*z, где z – простая импликанта, которая так же должна входить в f, т.к. в нее входит x. Но z будет поглощать х, поэтому х не может входить в f. Это и доказывает теорему Квайна.

Замечание: Заметим, что теорема Квайна применяется по отношению к функции СДНФ.

Порядок получения Сок. ДНФ может быть следующим:

1. Провести все операции неполного склеивания конституент единицы исходной СДНФ. Получатся произведения (n-1) ранга ; оставшиеся несклеенные конституенты единицы не могут участвовать в дальнейших склеиваниях.
2. Провести покрытие всех полученных произведений и конституент единицы. Часть некоторых конституент единицы будет устранена.
3. Продолжить, пока возможны операции 1) и 2).

Пример 1:

Если применим операцию полного склеивания, то получим:

или

или

т.е. у нас нет возможности далее провести операцию.

Применим теперь операцию неполного склеивания:

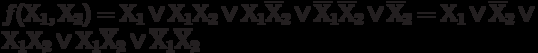
Простые импликанты: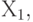  

Конституенты единицы:   

Теперь можем провести операции поглощения:

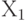 поглоща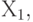ет:   

 поглощает: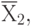   

Т.е. сокращенная ДНФ

 в данном случае она – минимальная форма.

Пример 2:

Пусть задана:

Получим СДНФ:

Теперь, имея СДНФ, можно получить сокращенную ДНФ:

Пример 3:

Склеиваются два произведения, содержащие число переменных с отрицанием, отличающихся на единицу и расположенных соответствующим образом.

Обычно произведение, содержащее ' n ' букв, называется минтермом ' n '- ранга.

Метод минимизации ФАЛ по Квайну

Определение: Тупиковой ДНФ называется дизъюнкция простых импликант, ни одну из которых из выражения функции исключить нельзя.

Этот метод минимизации ФАЛ заключается в следующем:

1. Находят Сок. ДНФ.
2. Находят все возможные тупиковые ДНФ.
3. Из найденных ТДНФ выбирают минимальную.

Иногда в Сок. ДНФ содержатся лишние импликанты. Как уже видели в сокращенной ДНФ:

импликанта \overline Х_{2}Х_{3} может быть исключена. Ни одной операции склеивания и поглощения к этой форме применить нельзя, т.к. это Сок. ДНФ, т.е. дизъюнкция простых импликант. Можно применить операцию развертывания по Х_{1}:

Т.к. Х_{1}Х_{3} покрывает Х_{1}\overline Х_{2}Х_{3}

и \overline Х_{1}\overline Х_{2} покрывает \overline Х_{1}\overline Х_{2}Х_{3}, то 

ТЕОРЕМА:

Всякая минимальная ДНФ является тупиковой. Обратное утверждение не справедливо. Доказательство очевидно.

Из этой теоремы вытекает важное следствие: Для того чтобы найти минимальную ДНФ, нужно найти все тупиковые формы и среди них взять минимальную.

Существует несколько различных способов отыскания тупиковых форм.

Выводы из данной статьи про совершенные дизъюнктивные указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое совершенные дизъюнктивные, конъюнктивные нормальные формы фал и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Цифровые устройства. Микропроцессоры и микроконтроллеры. принципы работы ЭВМ