Лекция
Сразу хочу сказать, что здесь никакой воды про модели сигналов, и только нужная информация. Для того чтобы лучше понимать что такое модели сигналов , настоятельно рекомендую прочитать все из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов.
Математическая модель сигнала устанавливает его связь (желательно однозначную) с информацией. Таким образом, сигнал можно рассматривать и как абстрактный, нематериальный объект. Уже давно математические модели сигналов используются для описания процессов обмена информацией. С появлением ЭВМ роль таких моделей существенно возросла. Со страниц научных статей, книг и учебников они переселились в недра специализированных ЭВМ - сигнальных процессоров. Математические модели позволяют классифицировать сигналы по наиболее общим признакам, отвлекаясь от конкретной формы физического процесса, им соответствующего.
Математические модели сигналов стали такими распространенными среди специалистов, что когда говорят «сигнал» почти всегда имеют в виду его математическую модель, а не физический процесс.
С математической точки зрения сигнал можно описать некоторой функцией времени. На рис. 3.1 приведен график некоторого сигнала S(t). Функция S(t) - непрерывная и однозначная функция времени. Для реальных сигналов однозначность фундаментальное физическое свойство, поскольку время течет в одном направлении (если бы это было не так, то как много ошибок можно было бы исправить!). Каждому значению функции S(t) в любой момент времени соответствует единственное значение сигнала - реального непрерывного физического процесса. Это означает, что математическая модель аналогична физическому сигналу, а, следовательно, и передаваемой информации.

Рис. 3.1. Математическая модель реального сигнала
Математические модели сигналов играют чрезвычайно важную роль при разработке принципов передачи, приема и обработки информации, а также на этапе проектирования аппаратуры и систем связи. Это связано с тем, что такие модели позволяют проводить анализ процессов в информационном канале с использованием математических методов, а, следовательно, в наиболее общей постановке. В результате выявляются фундаментальные закономерности, которые оберегают разработчиков от неоправданных затрат времени и средств на разработку заведомо неосуществимых идей.
Математическую модель, описанную выше, принято называть аналоговым сигналом. Иногда говорят о непрерывном сигнале, что ближе к сути этой математической модели.
Однако если обратится к телеграфии, то легко обнаружить, что с математической точки зрения сигнал может быть и дискретным. Передача в этом случае ведется дискретно символами азбуки. Мы уже затрагивали этот вопрос. Всерьез занялись дискретными сигналами в 30-х годах XX века в связи с нехваткой каналов связи (см. раздел 1.12). Оказалось, что без существенной потери информации непрерывный (аналоговый) сигнал можно заменить его дискретными значениями - отсчетами. Такой сигнал принято называть дискретным сигналом.
На рис. 3.2 приведена иллюстрация процедуры дискретизации математической модели сигнала. Отсчеты функции ?(/) берутся, как правило, с равномерным шагом по оси времени.
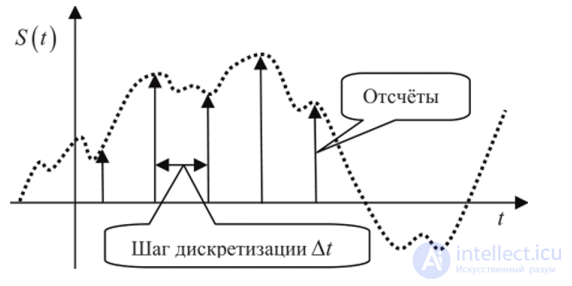
Рис. 3.2. Математическая модель дискретного сигнала
Обратите внимание на то, что мелкие (быстрые) подробности в результате дискретизации исчезают. Однако общая закономерность поведения сигнала сохраняется. В промежутках между отсчетами одного сигнала можно передавать отсчеты других сигналов. Так идея Э. Бодо нашла свое применение в телефонии (см. раздел 1.5).
Вид реального сигнала, соответствующего дискретному математическому сигналу, показан на рис. 3.3. Отсчетам сигнала ставятся в соответствие достаточно короткие импульсы, высота которых равна значению сигнала в точке отсчета . Такой элементарный сигнал называют импульсным сигналом.
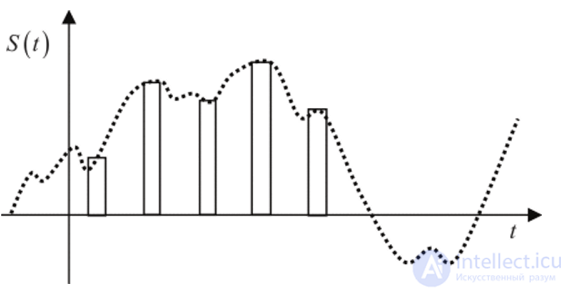
Рис. 3.3. Реальный дискретный (импульсный) сигнал
Выше мы говорили о том, что получателем информации, в конечном счете, является человек. Поэтому на выходе канала связи дискретный сигнал должен быть преобразован в непрерывный (аналоговый) сигнал. Ясно, что обратное восстановление происходит с ошибкой. Однако всегда можно установить допустимую погрешность восстановления. Ошибка восстановления увеличивается при действии на канал связи помех (см. разделы 1.8 и 1.12). В процессе развития систем связи были предложены методы уменьшения влияния помех на дискретный сигнал. Об этих методах вы узнаете при изучении специальных дисциплин.
Появление ЭВМ позволило сделать еще один, возможно самый важный шаг, в технике передачи информации - шаг к передаче дискретных отсчетов в форме двоичных чисел (см. раздел 1.12).
Кодирование информации с использованием двух состояний нам уже известно. В телеграфии это первым сделал П. Л. Шиллинг, который предложил шестизначный равномерный код (см. раздел 1.5). Затем появился неравномерный код С. Морзе. В телеграфии сигнал представляет собой буквы и цифры. Поэтому очень скоро появились устройства преобразования символов в импульсный код и обратно (аппараты Э. Бодо, раздел 1.5). С непрерывными сигналами ситуация сложнее.
Во-первых, значение сигнала в точке отсчета величина непрерывная, а двоичные числа дискретны и имеют ограничения по точности из-за конечной разрядности.
Во-вторых, надо было не только превратить отсчет в число, но восстановить исходный непрерывный сигнал.
Проблемы были решены благодаря прогрессу микроэлектронных технологий. В 70-х годах XX в. инженеры получили в свое распоряжение интегральные электронные схемы для преобразования аналогового сигнала в цифровой (АЦП) и цифрового в аналоговый (ЦАП). Об этом говорит сайт https://intellect.icu . Это привело к стремительному развитию цифровых систем передачи, приема, обработки и хранения сигналов.
Иллюстрация цифровой формы представления отсчетов приведена на рис. 3.4. В качестве примера выбрано кодирование четырехразрядными двоичными числами. Обратите внимание на ошибки по значению отсчетов, вызванные конечной разрядностью чисел (так называемый шум квантования).
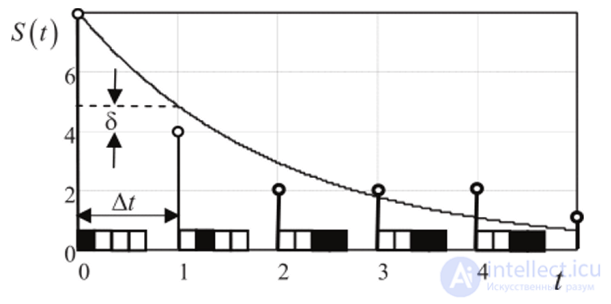
Рис. 3.4. Математическая модель цифрового сигнала:
At - шаг дискретизации, 5 - ошибка квантования; отчеты - 1000 (8), 0100 (4), ООН (2), ООП (2), 0011 (2), 0001 (1)
На рис. 3.5. показан реальный сигнал, наделенный евойст- вами числа в соответствии с моделью рис. 3.4. По виду графика нет никакой возможности установить является ли сигнал цифровым или это все лишь некоторая последовательность импульсов, неравномерно расположенных на оси времени. Преобразование в число станет возможным только, если будут известна система кодирования и, что не менее важно, начальная точка отсчета времени. До процедуры декодирования вообще не важно, что это за сигнал.

Рис. 3.5. Вид реального (аналогового) сигнала, соответствующего цифровому представлению дискретных отсчетов на рис. 3.4
Математические модели сигналов, о которых шла речь, можно представить в виде некоторой диаграммы. Эта диаграмма показана на рис. 3.6.

Рис. 3.6. Виды сигналов
Принцип действия всех цифровых устройств, включая ЭВМ и ваш ПК, базируется на реальных, непрерывных (аналоговых) физических явлениях в реальных физических объектах (электрических цепях). Переход на цифровую форму представления информации связан исключительно с тем, что мы наделяем эти процессы свойствами числа. Это всего лишь математическая модель, которая позволяет обращаться с такими сигналами как с числами. Этого можно было бы и не делать, но тогда описание процесса обработки сигнала стало бы крайне громоздким.
Возможно, вы обратили внимание на то, что дискретные, а тем более, цифровые сигналы недостоверно воспроизводят информацию. Да, это действительно так. Возникает вопрос, почему же в современных системах связи все шире используются именно такие сигналы.
Преимущества дискретных сигналов заключается, во- первых, в том, что появляется возможность уплотнения каналов связи. Во-вторых, цифровая форма сигналов позволяет реализовать такие численные математические методы обработки сигнала, которые не доступны аналоговым устройствам. Это преимущество особенно отчетливо проявляется при наличии в канале связи шумов и помех.
Как видите, радиоинженер должен владеть математикой, которая положена в основу теоретического фундамента радиотехники, радиоэлектроники и связи.
На современном этапе развития методов и технических средств обработки информации невозможно обойтись без навыков программирования, а профессиональное программирование невозможно без владения математикой.
Математические модели легли в основу всех разделов радиотехники - от теории цепей и сигналов до статистической радиотехники и современной теории информации.
В современных системах связи используют сложные сигналы (то есть имеющие сложные математические модели, описывающие поведение сигналов) и сложные методы их обработки. В то же время для описания сигналов любой сложности часто используются комбинации элементарных сигналов, модели которых описываются простыми математическими выражениями.
Так, для решения большого числа радиотехнических задач широкое применение находит функция включения (функция Хэвисайда) (рис.4.1.)
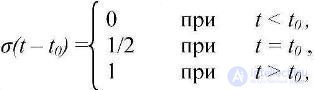 (4.1)
(4.1)
где t0 - задержка включения.
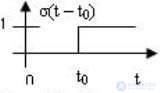
Рис. 4.1 Функция включения
Функция включения (ступенька) является математической абстракцией и в физически реализуемых устойствах в “чистом” виде не встречается. Ее можно рассматривать как предельный переход от ряда аналитических функций, например:
 (4.2)
(4.2)
С помощью этой функции (набора таких ступенек с разной амплитудой) с разной степенью точности можно описать характер поведения любой зависимости s(t) (рис.4.2), например, поведение электрической цепи при включении питания. Понятно, что для более точного описания радиотехнических сигналов нередко требуется уменьшение высоты каждой из используемых ступенек при одновременном увеличении количества самих ступенек.
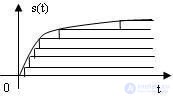
Рис. 4.2 Динамическое представление сигнала
Другим вариантом модели элементарного сигнала является прямоугольный импульс. Формально он может быть получен путем сложения двух функций включения различных полярностей σ(t - t1) и -σ(t - t2) с различными временами задержек t1 и t2 (рис. 4.3).
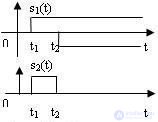
Рис. 4.3 Формирование прямоугольного импульса
Вариантом прямоугольного импульса является так называемый дельта-импульс, получаемый при предельным переходе от прямоугольного импульса, у которого с уменьшением длительности импульса, равной τ= (t2 - t1), одновременно увеличивается амплитуда Е при сохранении «площади» импульса, определяемой как S =τE (рис.4.4)
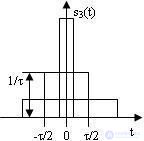
Рис. 4.4 Переход к дельта-функции
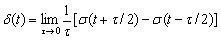 (4.3)
(4.3)
Дельта-функция δ(t) может быть интерпретирована как результат дифференцирования функции включения σ(t). Роль дельта-функций при анализе радиотехнических цепей и сигналов также велика, несмотря на то, что и дельта-функция является математической абстракцией. В частности, для определения импульсных характеристик радиотехнических устройств используются импульсные сигналы, длительность которых много меньше длительности реакции цепи на это воздействие.
Значительное место в ряду радиотехнических сигналов занимают периодические сигналы (рисунок 4.5), математические модели которых могут быть представлены выражением
s(t) = s(t + kT), (4.4)
где k - любое целое число, а Т - период сигнала (минимальный интервал времени между повторяющимися значениями сигнала).
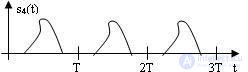
Рис. 4.5 Периодический сигнал
Периодические сигналы в силу своей регулярности являются хорошей основой для формирования различных тактирующих и синхронизирующих последовательностей, а также могут быть использованы в качестве несущих колебаний для различных видов модуляции.
Одним из наиболее известных периодических сигналов является гармоническая функция
s(t) = A cos(2πft+φ) = A cos(2πt/T+φ) = A cos(ωt+φ), (4.5)
где А - амплитуда гармонических колебаний; f - циклическая частота гармонических колебаний (величина, обратная периоду колебаний), f = 1/T; ω= 2πf - круговая частота гармонических колебаний; φ- начальный сдвиг фазы гармонического колебания.
Здесь и далее значения сигналов в текущий момент времени (мгновенное значение сигналов, например, s(t)) будем обозначать строчными буквами, для обозначения амплитуды колебаний будем использовать прописные буквы.
Поведение гармонического колебания во временной области показано на рисунке 4.6. При анализе радиотехнических устройств, кроме временного представления, также используется представление сигналов в частотной области.
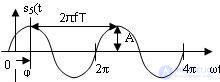
Рис. 4.6 Гармонический сигнал
Широкое применение гармонического сигнала объясняется универсальностью формы гармонического колебания. Эта универсальность заключается в том, что гармоническое колебание не изменяет свою форму при прохождении через линейные цепи (напомним, что в линейной цепи коэффициенты дифференциального уравнения, описывающего работу этой цепи, постоянны и не зависят от величины входного сигнала). При прохождении гармонического сигнала через линейную цепь форма (повторяющая синусоидальную зависимость) и частота этих колебаний остаются неизменными, могут измениться только амплитуда и начальная фаза.
Аналитическая форма - это запись закономерности в виде формулы
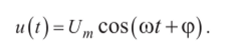
Графическое представление, которое получается в результате построения графика этой функции, дает наглядное представление о ее свойствах. На рис. 4.1 показано семейство графиков гармонического колебания для трех значений угла ср. Глядя на рисунок, легко установить параметры гармонического колебания.
Во-первых, гармоническое колебание изменяется во времени периодически. Период колебания равен Т. Во-вторых, его амплитуда (максимальное значение) равна Vт . Скорость изменения колебания во времени определяется круговой частотой (о, которая численно равна скорости изменения аргумента косинуса и измеряется в рад/с. В инженерной практике вместо круговой частоты используют циклическую частоту (или просто частоту) / = /Т. Она показывает какое число периодов укладывается на отрезке времени в одну секунду. Циклическая частота измеряется в герцах (Гц). Наконец, (р - это начальная фаза колебания. Для одиночного гармонического колебания в фазе мало смысла, но когда колебаний несколько, то (р дает представление о расположении колебаний на оси времени друг относительно друга. Если ср > 0, то второе колебание сдвинуто влево, т. е. опережает первое, а если (р < 0 , то ситуация обратная (см. рис. 4.1).
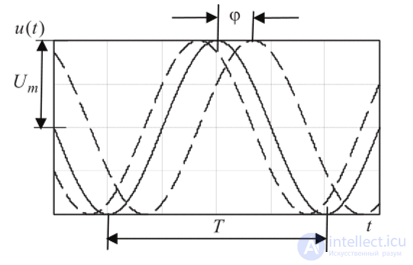
Рис. 4.1. Гармоническое колебание
Векторное представление гармонических колебаний на плоскости делает очень наглядным фазовые и амплитудные соотношения между ними. Строгое обоснование этого приема вам изложат на старших курсах. Мы же поступим формально.
Обратите внимание, что если частота колебания задана, то все значения на оси времени становятся известными, если известны начальная фаза и амплитуда, т. е. значение и(/) при 1 = 0, которое равно

Если принять иза гипотенузу прямоугольного треугольника, то м(0) будет выступать в роли его катета. Следовательно, гармоническому колебанию можно поставить в соответствие геометрическое представление, показанное на рис. 4.2.
Отрезок, имеющий длину и направление, в математике рассматривается как вектор. На рис 4.2 гипотенуза изображена в виде вектора длиной ит , который образует угол (р > 0 с горизонтальной осью. Такое представление гармонического колебания называют векторной диаграммой.
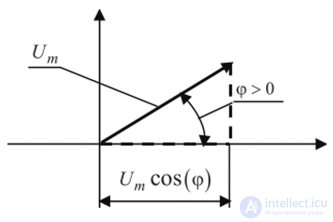
Рис 4.2. Векторная диаграмма
Удобство использования векторной диаграммы становиться очевидным при сложении нескольких гармонических колебаний. Вот простой, но очень показательный пример. Пусть

Конечно, можно воспользоваться формулами тригонометрии. При равных амплитудах это сделать нетрудно. Но посмотрите насколько проще решается эта задача с помощью векторной диаграммы. Воспользуемся векторными построениями для решения этой задачи. На рис. 4.3 представлено ее графическое решение.
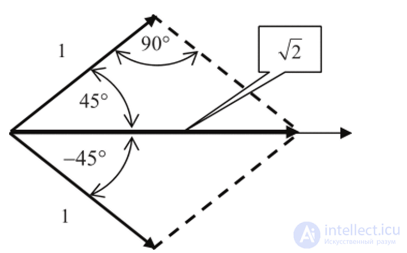
Рис. 4.3. Сложение двух гармонических колебаний
Прежде всего, построим два вектора длиной, равной 1 и образующих с горизонтальной осью углы ±45°. Используя известное со школьных лет правило сложения векторов по правилу параллелограмма, находим суммарный вектор. Он будет направлен по биссектрисе угла между векторами, т. е. по горизонтальной оси (ср = 0). Длина суммарного вектора равна рана
квадратному корню из суммы квадратов катетов (Vт = [2 ). Итак ответ очевиден:
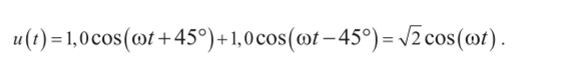
Вы можете возразить, что графическое сложение векторов не очень-то точная процедура. Да, это действительно так. Однако в инженерной практике очень часто из-за дефицита времени достаточно и приближенного качественного ответа. Нужно также помнить и том, что точность номиналов комплектующих изделий редко превышает 10%. Наконец, получив приближенный ответ, можно его уточнить, обратившись к компьютеру (если это нужно, а потеря времени оправдана).
Статью про модели сигналов я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое модели сигналов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Комментарии
Оставить комментарий
Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Термины: Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов