Лекция
Сразу хочу сказать, что здесь никакой воды про амплитудная модуляция, и только нужная информация. Для того чтобы лучше понимать что такое амплитудная модуляция , настоятельно рекомендую прочитать все из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов.
В процессе амплитудной модуляции амплитуда U0 несущего колебания u0 (t) = U0 cos(ωt+φ) перестает быть постоянной и изменяется по закону передаваемого сообщения. Амплитуда U(t) несущего колебания может быть связана с передаваемым сообщением соотношением:
U(t) = U0 + kA e(t), (5.1)
где U0 - амплитуда несущего колебания в отсутствии сообщения (немодулированное колебание); e(t) - функция, зависящая от времени, соответствующая передаваемому сообщению (ее называют модулирующим сигналом); kA - коэффициент пропорциональности, отражающий степень влияния модулирующего сигнала на величину изменения амплитуды результирующего сигнала (модулированного колебания).Выражение для амплитудно-модулированного сигнала в общем случае имеет вид:
uАМ(t) = [U0 + kA e(t)] cos(ω0t+φ). (5.2)
Простейший для анализа случай амплитудно-модулированного колебания получается, если в качестве модулирующего сигнала используется гармоническое колебание (такой случай называется тональной модуляцией):e(t) = E cos(´Ωt+Θ), (5.3)
где Е - амплитуда, ´Ω - угловая частота; Θ - начальная фаза модулирующего сигнала.Для упрощения анализа будем полагать начальные фазы колебаний равными нулю, что не повлияет на общность выводов. Тогда для тональной амплитудной модуляции можно записать:
uАМ(t) = [U0 + kA E cos´Ωt] cosω0t = U0 [1+ MA cos´Ωt] cosω0t, (5.4)
где МA = Е/U0 - коэффициент амплитудной модуляции (иногда говорят - глубина амплитудной модуляции).Для определения спектра амплитудно-модулированного колебания выполним несложные преобразования выражения (5.4):
uАМ(t) =U0 cosω0t + U0 MA cos´Ωt cosω0t = U0 cosω0t + (U0 MA/2) cos(ω0 - ´Ω)t + (U0 MA/2) cos(ω0 + ´Ω)t. (5.5)
Из анализа выражения (5.5) следует, что при амплитудной модуляции гармоническим колебанием спектр амплитудно-модулированного сигнала содержит три гармонические составляющие. Гармоническая составляющая с частотой, равной ω0, представляет собой исходную немодулированную несущую с частотой ω0 и амплитудой U0.
Гармонические составляющие с частотами, равными (ω0 - ´Ω) и (ω0 + ´Ω) представляют собой продукт амплитудной модуляции и называются, соответственно, нижней и верхней боковыми составляющими. Амплитуды боковых составляющих одинаковы, равны U0MA/2 и расположены симметрично относительно несущей частоты ω0 на расстоянии, равном - ´Ω. Таким образом, ширина полосы частот Δω, занимаемая амплитудно-модулированным колебанием при модуляции гармоническим сигналом с частотой ´Ω, равна Δω =2´Ω.
Графики несущего колебания u0(t), модулирующего сигнала е(t) и амплитудно-модулированного сигнала uАМ(t) приведены на рисунке 5.1.
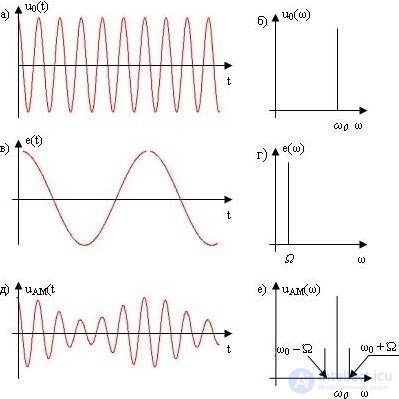
Рис. 5.1 Тональная
амплитудная модуляция :
а) несущее колебание и его спектр (б);
в) модулирующий сигнал и его спектр (г);
д) амплитудно-модулированное колебание и его спектр (е)
При отсутствии модуляции (МA = 0) амплитуды боковых составляющих равны нулю и спектр амплитудно-модулированного сигнала состоит только из несущего колебания с частотой ω0. Об этом говорит сайт https://intellect.icu . При коэффициенте амплитудной модуляции МA < 1 амплитуда результирующего колебания изменяется от максимального значения UMAX = U0(1 + MA) до минимального UMIN = U0(1 - MA).
Таким образом, коэффициент МA амплитудной модуляции может быть определен как
МA = (UMAX - UMIN)/(UMAX + UMIN). (5.6)
При коэффициенте амплитудной модуляции МA >1 возникают искажения, называемые перемодуляцией (рисунок 5.2). Такие искажения могут приводить к потере информации и их стараются не допускать.
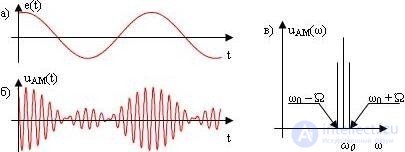
Рис. 5.2 Тональная амплитудная модуляция при коэффициенте МA > 1:
а) модулирующий сигнал; б) амплитудно-модулированное колебание и его спектр (в)
Подобный подход можно применить и к анализу амплитудно-модулированных колебаний сложной формы. В этом случае периодический модулирующий сигнал может быть представлен набором гармонических составляющих, частота которых кратна периоду исходного сигнала. Каждая из гармоник модулирующего сигнала сформирует в спектре амплитудно-модулированного колебания две боковые составляющие, симметрично отстоящие от несущей на величину, равную частоте соответствующей гармоники. Для примера, если спектр модулирующего сигнала имеет вид, представленный на рисунке 5.3,а, то спектр амплитудно-модулированного колебания может быть представлен диаграммой, приведенной на рисунке 5.3,б.
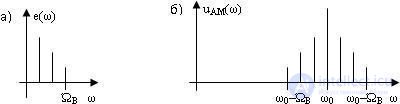
Рис. 5.3 Спектры сигналов: а) модулирующего сигнала; б) амплитудно-модулированного колебания
В общем случае, ширина ПАМ спектра амплитудно-модулированного колебания равна
ПАМ = 2 ´ΩВ, (5.7)
где ´ΩВ верхняя (наибольшая) частота в спектре модулирующего сигнала.
Амплиту́дная модуляция — вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда
Первый опыт передачи речи и музыки по радио методом амплитудной модуляции произвел в 1906 году американский инженерР. Фессенден. Несущая частота 50 кГц радиопередатчика вырабатывалась машинным генератором (альтернатором), для ее модуляции между генератором и антенной включался угольный микрофон, изменяющий затухание сигнала в цепи. С 1920 года вместо альтернаторов стали использоваться генераторы на электронных лампах. Во второй половине 1930-х годов, по мере освоения ультракоротких волн, амплитудная модуляция постепенно начала вытесняться из радиовещания и радиосвязи на УКВ частотной модуляцией. С середины XX века в служебной и любительской радиосвязи на всех частотах внедряетсямодуляция с одной боковой полосой (ОБП), которая имеет ряд важных преимуществ перед АМ. Поднимался вопрос о переводе на ОБП и радиовещания, однако это потребовало бы замены всех радиовещательных приемников на более сложные и дорогие, поэтому не было осуществлено. В конце XX века начался переход к цифровому радиовещанию с использованием сигналов с амплитудной манипуляцией.
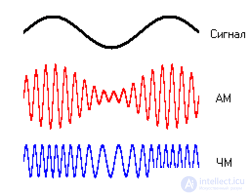
Пусть
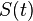 — информационный сигнал,
— информационный сигнал, 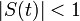 ,
,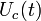 — несущее колебание.
— несущее колебание.Тогда амплитудно-модулированный сигнал 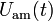 может быть записан следующим образом:
может быть записан следующим образом:
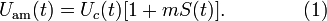
Здесь  — некоторая константа, называемая коэффициентом модуляции. Формула (1) описывает несущий сигнал
— некоторая константа, называемая коэффициентом модуляции. Формула (1) описывает несущий сигнал 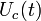 , модулированный по амплитуде сигналом
, модулированный по амплитуде сигналом 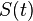 с коэффициентом модуляции
с коэффициентом модуляции  . Предполагается также, что выполнены условия:
. Предполагается также, что выполнены условия:
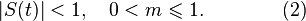
Выполнение условий (2) необходимо для того, чтобы выражение в квадратных скобках в (1) всегда было положительным. Если оно может принимать отрицательные значения в какой-то момент времени, то происходит так называемая перемодуляция(избыточная модуляция). Простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями.
Допустим, что мы хотим промодулировать несущее колебание моногармоническим сигналом. Выражение для несущего колебания с частотой 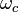 , начальную фазу положим равной нулю, имеет вид
, начальную фазу положим равной нулю, имеет вид
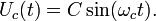
Выражение для модулирующего синусоидального сигнала с частотой 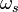 имеет вид
имеет вид
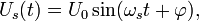
где 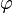 — начальная фаза. Тогда, в соответствии с (1)
— начальная фаза. Тогда, в соответствии с (1)
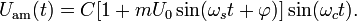
Приведенная выше формула для 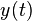 может быть записана в следующем виде:
может быть записана в следующем виде:
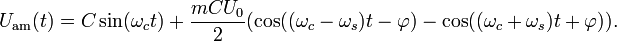
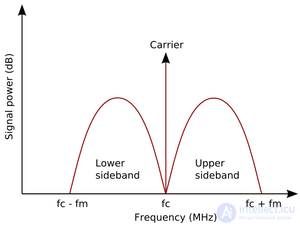
Радиосигнал состоит из несущего колебания и двух синусоидальных колебаний, называемых боковыми полосами, каждое из которых имеет частоту, отличную от 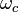 . Для синусоидального сигнала, использованного здесь, частоты равны
. Для синусоидального сигнала, использованного здесь, частоты равны 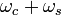 и
и 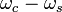 . Пока несущие частоты соседних радиостанций достаточно разнесены, и боковые полосы не перекрываются между собой, станции не будут влиять друг на друга.
. Пока несущие частоты соседних радиостанций достаточно разнесены, и боковые полосы не перекрываются между собой, станции не будут влиять друг на друга.
Статью про амплитудная модуляция я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое амплитудная модуляция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Из статьи мы узнали кратко, но содержательно про амплитудная модуляция
Комментарии
Оставить комментарий
Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Термины: Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов