Лекция
Сразу хочу сказать, что здесь никакой воды про общая теория преобразования частоты, и только нужная информация. Для того чтобы лучше понимать что такое общая теория преобразования частоты , настоятельно рекомендую прочитать все из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов.
Цель анализа.
При анализе ПЧ решают две основные задачи:
1) определяют входное напряжение 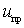 , для чего находят полезную составляющую тока
, для чего находят полезную составляющую тока 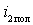 промежуточной частоты, которая совпадает с резонансной частотой фильтра, после чего рассчитывают основные показатели преобразователя - коэффициент усиления, АЧХ, ФЧХ и т.д.;
промежуточной частоты, которая совпадает с резонансной частотой фильтра, после чего рассчитывают основные показатели преобразователя - коэффициент усиления, АЧХ, ФЧХ и т.д.;
2) находят составляющую входного тока преобразователя на частоте 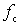 , создающую нагрузку для источника сигнала.
, создающую нагрузку для источника сигнала.
Для упрощения анализ проводят при следующих допущениях:
а) Смеситель любого преобразователя частоты рассматриваем как нелинейный шестиполюсник, на выходе которого включена избирательная нагрузка 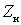 , настроенная на промежуточную частоту.
, настроенная на промежуточную частоту.

Pисунок 11.3.
б) Полагаем, что на нелинейный элемент действуют три гармонических напряжения:
- напряжение сигнала 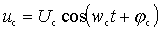 ;
;
- напряжение промежуточной частоты 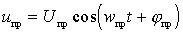 ;
;
- напряжение гетеродина 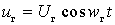 .
.
в) Считаем, что 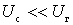 и
и  , т.е. полагаем нелинейный элемент работающим в линейном режиме по отношению к напряжению сигнала; относительно напряжения гетеродина нелинейный элемент всегда работает в нелинейном режиме.
, т.е. полагаем нелинейный элемент работающим в линейном режиме по отношению к напряжению сигнала; относительно напряжения гетеродина нелинейный элемент всегда работает в нелинейном режиме.
г) Считаем нелинейный элемент смесителя безынерционным устройством, не содержащим емкостных и индуктивных элементов. Поэтому его ток не зависит от производных или интегралов приложенных к нелинейному элементу напряжений. Для безынерционного НЭ входной и выходной токи определяются статическими ВАХ:
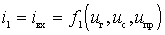 ,
,
 .
.
Game: Perform tasks and rest cool.6 people play!
Play gameТ.к.  и
и  малы, то ток
малы, то ток

можно разложить в ряд Тейлора по двум переменным, ограничившись учетом членов ряда с  и
и  в первой степени:
в первой степени:
 .(**)
.(**)
Первое слагаемое представляет собой составляющую выходного тока, которая обусловлена действием напряжения гетеродина при  . Введем обозначение
. Введем обозначение
 .
.
Второе слагаемое 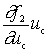 характеризует приращение входного тока, которое вызвано действием сигнала.
характеризует приращение входного тока, которое вызвано действием сигнала.
 - мгновенное значение проводимости прямого действия или крутизна НЭ периодически изменяющаяся во времени под действием напряжения гетеродина.
- мгновенное значение проводимости прямого действия или крутизна НЭ периодически изменяющаяся во времени под действием напряжения гетеродина.
Третье слагаемое  является приращением выходного тока смесителя в результате действия на его выходе напряжения промежуточной частоты.
является приращением выходного тока смесителя в результате действия на его выходе напряжения промежуточной частоты.
 - мгновенное значение выходной проводимости смесителя, изменяющаяся во времени под действием напряжения гетеродина.
- мгновенное значение выходной проводимости смесителя, изменяющаяся во времени под действием напряжения гетеродина.
Согласно линейной теории преобразователей частоты в выражении (**) учитываются первые три члена; при этом ток 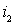 линейно зависит от
линейно зависит от  и
и  . Об этом говорит сайт https://intellect.icu . С учетом принятых обозначений можно записать
. Об этом говорит сайт https://intellect.icu . С учетом принятых обозначений можно записать
 .
.
Поскольку величины  ,
, 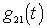 и
и 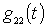 определяются при наличии напряжения гетеродина и периодически с частотой
определяются при наличии напряжения гетеродина и периодически с частотой 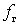 меняются во времени, то их можно представить рядами Фурье:
меняются во времени, то их можно представить рядами Фурье:
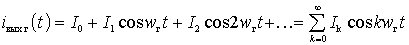 ;
;
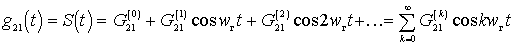 ;
;
 .
.
Полученные ряды содержат только косинусоидальные члены, т.к. , а НЭ считаем безынерционным.
, а НЭ считаем безынерционным.
Подставив полученные соотношения в выражение для 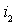 , получим:
, получим:
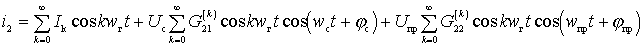 .
.
или , используя правило перемножения косинусов, получим
 .(*)
.(*)
Из двух последних соотношений видно, что выходной ток смесителя содержит составляющие с частотами  и комбинационные составляющие с частотами
и комбинационные составляющие с частотами
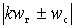 и
и  .
.
Преобразование частоты возможно на любой гармонике крутизны:
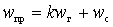 ;
;
Game: Perform tasks and rest cool.6 people play!
Play game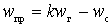 при
при  ;
;
 при
при 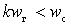 .
.
Из этих значений используют только одно. Если при 
 , то преобразование частоты называют простым. Если при
, то преобразование частоты называют простым. Если при 
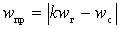 , то преобразование частоты называют комбинационным, оно возможно из-за появления гармоник крутизны.
, то преобразование частоты называют комбинационным, оно возможно из-за появления гармоник крутизны.
Таким образом, из всех составляющих выходного тока полезной будет только составляющая с частотой  .
.
Определим в выражении (*) составляющую тока с частотой  . За счет второго слагаемого при
. За счет второго слагаемого при  и третьего слагаемого при
и третьего слагаемого при 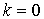 будем иметь
будем иметь
 ;
;
или
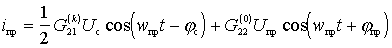 .(-)
.(-)
Переходя к комплексным амплитудам, данное выражение можно записать
 ,(+)
,(+)
где  ;
; 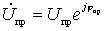
Это соотношение называется уравнением прямого преобразования частоты. Первое слагаемое уравнений (-) и (+) характеризует процесс преобразования частоты. Второе слагаемое обусловлено реакцией нагрузки, поскольку величина  зависит от сопротивления нагрузки
зависит от сопротивления нагрузки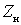 .
.
Определение полезной составляющей входного тока (обратное преобразование частоты).
В смесителе наряду с прямым возможно и обратное преобразование частоты. Физический смысл его заключается в том, что, если к входным зажимам смесителя приложить напряжение промежуточной частоты, то при наличии гетеродинного напряжения, через входные зажимы смесителя будет протекать ток с частотой сигнала. Такое преобразование частоты возможно лишь в том случае, если смеситель обладает нелинейной проводимостью обратного действия, периодически изменяющейся с частотой гетеродина. Обратное преобразование частоты изменяет входную и выходную проводимости смесителя. в наибольшей степени это проявляется в диодных ПЧ.
Уравнение обратного преобразования частоты можно получить представляя входной ток  как функцию напряжения гетеродина
как функцию напряжения гетеродина 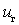 и двух малых переменных
и двух малых переменных  и
и  .
.
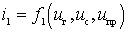 .
.
Разложив эту функцию в ряд Тейлора по двум переменным  и
и . и ограничиваясь линейными членами, получают
. и ограничиваясь линейными членами, получают
 .
.
где 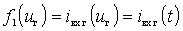 - ток на входе НЭ, обусловленный действием напряжения гетеродина;
- ток на входе НЭ, обусловленный действием напряжения гетеродина;
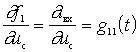 - мгновенное значение входной проводимости НЭ;
- мгновенное значение входной проводимости НЭ;
 - мгновенное значение проводимости обратной связи НЭ.
- мгновенное значение проводимости обратной связи НЭ.
Действуя аналогично случаю прямого преобразования частоты, в итоге для обратного преобразования частоты можно получить
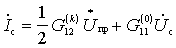 ,
,
где 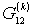 - амплитуда k-й гармоники проводимости обратного преобразования
- амплитуда k-й гармоники проводимости обратного преобразования  для напряжения промежуточной частоты;
для напряжения промежуточной частоты;
Game: Perform tasks and rest cool.6 people play!
Play game - постоянная составляющая входной проводимости
- постоянная составляющая входной проводимости 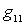 для напряжения сигнала.
для напряжения сигнала.
Внутренние параметры преобразователя частоты.
На основании уравнений прямого и обратного преобразований определим внутренние параметры преобразователя, т.е. параметры, не зависящие от сопротивления нагрузки и сопротивления источника сигнала.
а) Внутренняя проводимость прямого действия (крутизна прямого преобразования) определяется как отношение амплитуды тока промежуточной частоты к амплитуде напряжения входного сигнала при закороченном выходе ( 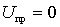 ):
):
 ;
;
б) Внутренняя выходная проводимость преобразователя равна отношению амплитуды тока промежуточной частоты к амплитуде напряжения этой же частоты при закороченном входе ( ):
):
 ;
;
в) Внутренняя проводимость обратного действия (крутизна обратного преобразования  ) вычисляется как отношение амплитуды составляющей тока с частотой сигнала к амплитуде напряжения промежуточной частоты при закороченном входе (
) вычисляется как отношение амплитуды составляющей тока с частотой сигнала к амплитуде напряжения промежуточной частоты при закороченном входе ( ):
):
 ;
;
г) Внутренняя входная проводимость равна отношению амплитуды составляющей тока с частотой сигнала к амплитуде напряжения этой же частоты, при закороченных выходных зажимах (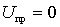 ):
):
 .
.
В общем случае при инерционном характере проводимости нелинейного элемента, внутренние параметры смесителя являются комплексными величинами. Поэтому уравнения, характеризующие работу смесителя целесообразно записать в виде:
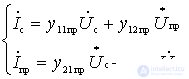 .
.
Таким образом, преобразующий элемент совместно с гетеродином можно представить в виде квазилинейного четырехполюсника, характеризуемого четырьмя y- параметрами - преобразовательными параметрами.
Внешние параметры преобразователя.
Эквивалентные схемы замещения усилительных элементов усилительного и преобразовательного каскадов ничем внешне не отличаются. Отличие состоит только в значении параметров. Поэтому аналогично усилительному ( резонансному) каскаду определим внешние параметры преобразователя.

Pисунок 11.4.
а) Коэффициент усиления
 .
.
б) Входная проводимость
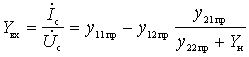 .
.
в) Выходная проводимость
 .
.
где 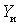 - проводимость источника сигнала;
- проводимость источника сигнала;
 - проводимость нагрузки.
- проводимость нагрузки.
Статью про общая теория преобразования частоты я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое общая теория преобразования частоты и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Из статьи мы узнали кратко, но содержательно про общая теория преобразования частоты
Комментарии
Оставить комментарий
Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов
Термины: Устройства приема и обработки радиосигналов, Передача, прием и обработка сигналов