Общий анализ резонансного усилителя кратко

Эквивалентная схема усилительного прибора.

В режиме малых сигналов транзистор или лампу можно представить активным линейным четырехполюсником с зависимым генератором тока.

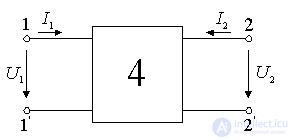
Pисунок 9.4.

Такой четырехполюсник описывается двумя линейными уравнениями, связывающими между собой напряжения и токи на его входе и выходе. Положительные направления токов и напряжений указаны на рисунке стрелками. Мы будем пользоваться системой y-параметров, т.к. на высоких частотах она наиболее удобна. В системеy-параметров уравнения четырехполюсника имеют вид:

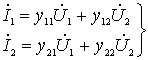Напомним, что y-параметры определяются при коротком замыкании на входе и выходе:

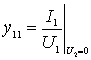- входная проводимость четырехполюсника при КЗ на выходе;

- обратная проводимость при КЗ на входе;

- прямая проводимость при КЗ на выходе (крутизна);

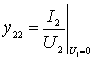- выходная проводимость при КЗ на входе.

Анализ конкретных схем усилителей более нагляден, если использовать эквивалентные схемы, полученные на основе, теории четырехполюсников. Наибольшее распространение получила следующая эквивалентная схема усилительного прибора.

Pисунок 9.5.

Для дальнейшего анализа y-параметры удобно представить в виде:

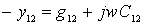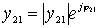где 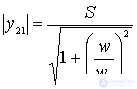; 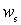- частота, на которой , т.е. крутизна уменьшается в 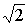раз.

Эквивалентная схема усилителя.

Полная эквивалентная схема усилителя содержит источник сигнала и нагрузку.

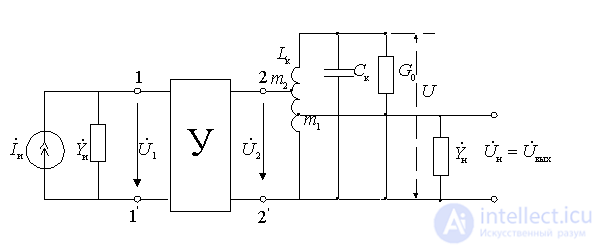
Pисунок 9.6.

Для этой схемы

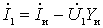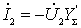знак "-" в данном выражении появляется вследствие того, что напряжение на нагрузке четырехполюсника (в точках 2-2') от тока 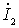будет противоположным по знаку напряжению ;

где 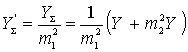- суммарная проводимость контура и нагрузки, пересчитанная к выходу четырехполюсника, т.е. Об этом говорит сайт https://intellect.icu . к точкам 2-2'.

На схеме показано неполное включение контура. Коэффициенты включения

Основные характеристики усилителя.

Определим основные характеристики усилителя. Коэффициент каскада

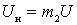Отношение 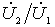найдем из второго уравнения четырехполюсника

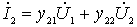Подставим сюда

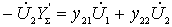отсюда

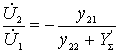Подставим полученное отношение в выражение для К

или, если подставить значение

где 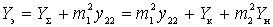- полная эквивалентная проводимость контура.

Полную эквивалентную проводимость контура можно выразить через эквивалентную резонансную проводимость контура и обобщенную расстройку

,

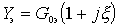- эквивалентная резонансная проводимость контура;

- обобщенная расстройка.

Тогда

.

Модуль коэффициента усиления

.

При 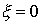находим резонансный коэффициент усиления

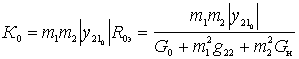Поскольку зависит от коэффициентов и , то должны существовать оптимальные значения этих коэффициентов, при которых будет максимальным.

Исследование выражения для на максимум позволяет найти оптимальные значения коэффициентов

где .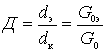

Подставив полученные значения 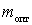в выражение для , найдем максимальный коэффициент усиления

Из последних выражений видно, что резонансный коэффициент усиления достигает своего максимального значения при одинаковом шунтировании контура со стороны выхода активного элемента данного каскада и со стороны нагрузки, т.е. когда

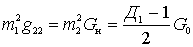Выражение для показывает, что при малом собственном (конструктивном) затухании контура, т.е. при Д>>1, усиление достигает своего предельного для данного активного элемента значения

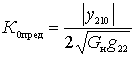Если же конструктивное затухание контура велико, близко к эквивалентному, заданному из условия получения требуемой избирательности, то усиление получается малым, т.к. при , 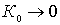. Отсюда ясно, что контур нужно стремиться выполнять с возможно меньшим собственным затуханием.

Выведем уравнение резонансной кривой усилителя:

Т.е. на резонансную характеристику усилителя кроме собственно резонансных свойств влияет зависимость коэффициентов , и крутизны от расстройки. При малых расстройках можно пренебречь изменением , и . Тогда

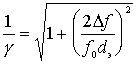Отсюда можно найти полосу пропускания усилителя при заданной неравномерности .

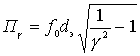При .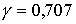

Фазовая характеристика усилителя имеет вид

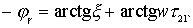Определим входную проводимость каскада усилителя (в точках 1-1' полной эквивалентной схемы).

Из первого уравнения четырехполюсника получим

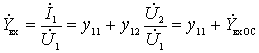Подставляя сюда найденное нами ранее значение , получим

или, с учетом того, что 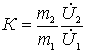и 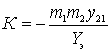, получим

В полученных выражениях для 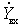второе слагаемое обусловлено проводимостью внутренней обратной связи активного элемента .

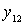Аналогично можно найти выходную проводимость активного элемента ( в точках 2-2' полной эквивалентной схемы):

Структура выражений (+) и (*) одинакова вследствие уравнений четырехполюсника относительно входных и выходных напряжений и токов. Из полученных выражений видно, что из-за внутренней ОС, обусловленной проводимостью 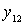, входная проводимость зависит от проводимости нагрузки, а выходная - от проводимости источника сигнала.

Вау!! 😲 Ты еще не читал? Это зря!

• схемы резонансных усилителей ,