Структурная избыточность - Структурный анализ, Структурно – топологические характеристики систем.

Это окончание невероятной информации про структурный анализ.

...

реализации проекта возможны 4 варианта. Их вероятность определяется по правилу вероятности сложных событий.
Сложное событие – это событие В, которое произошло при условии, что перед ним произошло другое событие А. Известно, что события А и В независимы. Отметим
P(A) - вероятность реализации события А,
P(B) – вероятность реализации события В,
P(B|A) - условная вероятность реализации события В, в случае, что перед ним имело место событие А.

Тогда имеет место соотношение
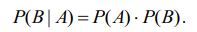. (3.1)

Формулу (1) называют формулой вероятности сложного события.
Таким образом, вероятность первого варианта событий равна P=0.4·0.2=0.08;
Вероятность второго варианта событий равна P=0.4·0.8=0.32;
Вероятность третьего варианта событий равна P=0.6·0.4=0.24;
Вероятность четвертого варианта событий равна P=0.6·0.6=0.36.
Сумма вероятностей равна 1, то есть рассмотрены нами 4 варианта развития события.
образуют полную группу событий.
Полная группа событий, это такой перечень возможных событий, одно из которых имеет
обязательно состояться.

Например: моя оценка по экономической кибернетике – ”2”, ”3”, ”4”, ”5”, ”н”.
Пусть система может находиться в n различных несовместимых состояниях S1 S2 Sn

Вероятность каждого из состояний P1 P2 Pn

. Если выполняется равенство 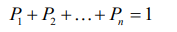(3.2)
группа состояний S1 S2 Sn называется полной.

Рассчитаем ожидаемую прибыль за второй год реализации проекта:
Z = p1 · z1 + p2 · z2 + p3 · z3 + p4 · z4 = 400 · 0.08 + 300 · 0.32 + 300 · 0.24 + 200 · 0.36 = 32+96+72+72=272 (тыс. долларов .)

Пример 2. Анализ вероятных вариантов получения высшего образования.
Выпускник школы планирует поступать в университет или в колледж. Соответствующие
вероятности составляют 0.7 (университет) и 0.3 (колледж). После окончания колледжа выпускник планирует работать референтом (зарплата 1500 долларов ).

В случае поступления в университет выпускник планирует учиться по направлению
"Экономическая кибернетика" (вероятность 0.6) или же по направлению "Документознавство” (вероятность 0.4). После окончания учебы по направлению "Документоведение" выпускник планирует работать в отделе кадров (зарплата 2500 долларов ).

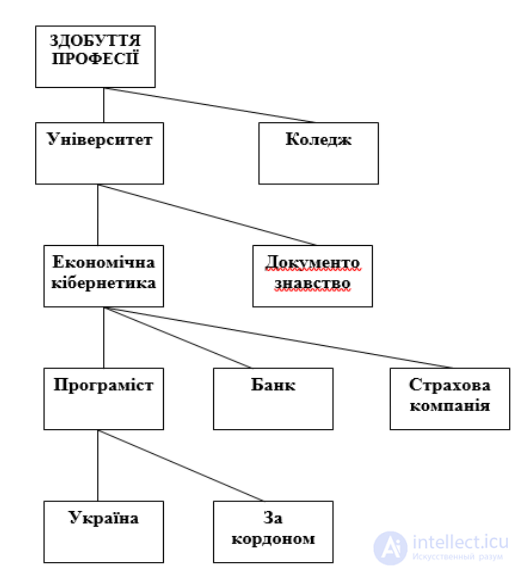
В случае окончания обучения по направлению "Экономическая кибернетика" выпускник планирует устроиться на работу в страховую компанию (зарплата 4000 долларов ,
вероятность 0.45) или же в банк (5000 долларов , вероятность 0.4), или же работать программистом (вероятность 0.15).

В случае работы программистом рассматриваются два варианта: работа в США (зарплата 10000 долларов , вероятность 0.75) и работа на Марсе (зарплата 35 000 долларов , вероятность 0.25).
Для экономической оценки перспектив рассматриваемых вариантов следует учитывать как экономическую выгоду, так и вероятность соответствующего варианта. Если событие является результатом цепочки предыдущих событий, то это сложное событие и его вероятность.

оценивают как произведение вероятностей всех предыдущих событий. На каждом уровне
эволюции процесса следует проверять формулу полной группы событий (сумма вероятностей равна единице).

Этап 1. Экономическая оценка перспективности варианта "поступление в колледж"
определяется как произведение вероятности и ожидаемого дохода
Z = p1 · z1 = 1500 · 0.3 = 450 (долларов )
Этап 2. При использовании формулы сложной вероятности определяем экономическую оценку перспективности варианта «университет» + «Документоведение»
Z = p2 · z2 = 2500 · 0.7 · 0.4 = 700 (долларов )
Этап 3. Определяем экономическую оценку перспективности варианта "университет" + "Экономическая кибернетика" + "Страховая компания"
Z = 4000 · 0.7 · 0.6 · 0.45 = 756 (долларов )
Определяем экономическую оценку перспективности варианта «университет» +
"Экономическая кибернетика" + "Банк"
Z = 5000 · 0.7 · 0.6 · 0.4 = 840 (долларов )
Этап 4. Определяем экономическую оценку перспективности варианта Университет + Экономическая кибернетика + Программист + Украина
Z = 10 000 · 0.7 · 0.6 · 0.15 · 0.7 = 441 (долларов )
Определяем экономическую оценку перспективности варианта «университет» +
"Экономическая кибернетика" + "Программист" + "за границу"
Z = 35 000 · 0.7 · 0.6 · 0.15 · 0.3 = 661 (долларов )
Вывод. Из всех просмотренных вариантов наиболее экономически перспективен вариант «университет» + «Экономическая кибернетика» + «Банк».

3.3. Структурный анализ дерева отказов

Анализ дерева отказов (АДВ) считается одним из наиболее полезных аналитических инструментов в процессе оценки безопасности эксплуатации сложных систем. Этот метод использует дедуктивный логический метод (движение от общего
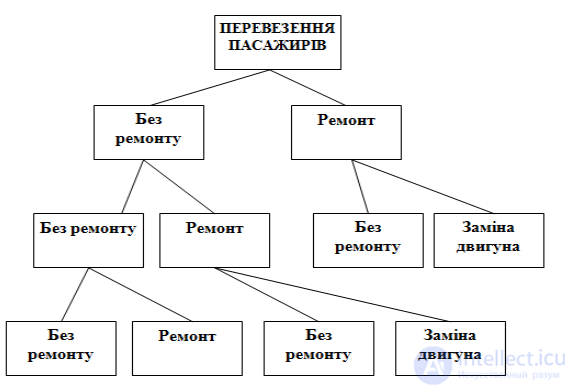
к частичному). Как правило, нежелательные события происходят под влиянием различных факторов. Дерево отказов позволяет проанализировать действие этих факторов на разных этапах работы системы. При анализе дерева отказов нежелательное событие (авария, банкротство) считают конечной точкой схемы. Рассматривая отдельные события, предшествовавшие конечному событию, строят дерево отказов. Примером дерева отказа является анализ перевозок на автобусе с учетом вероятности поломок автобуса.

Пример 3. Системный анализ пассажирских перевозок
Методику системного анализа рассмотрим на примере анализа системы междугородных пассажирских перевозок.
Основные характеристики маршрута.
Примерный годовой доход – 700 тыс. долларов.
Цена нового автобуса – 300 тыс. долларов. Цена б/у автобуса – 150 тыс. долларов.
Стоимость ремонта двигателя – 40 тыс долларов.
Установка нового двигателя – 100 тыс. долларов.

После 2-й поломки двигателя (или б/у после 1 поломки) – замена двигателя.
Годовой эксплуатационный расход: новый автобус – 300 тыс. долларов. БВ автобус – 450 тыс. долларов.
Стартовый капитал предпринимателя – 300 тыс. долларов.

Таблица 1. Вероятность поломки двигателя

Задача. Составить бизнес-план работы на 3 года, подсчитав ожидаемую прибыль для каждого года.
Система может находиться в двух состояниях:
S1 ‒ двигатель работает;
S2 ‒ двигатель не работает.

Вероятность первого состояния обозначим p

вероятность второго q

. Поскольку события S1 и S2 образуют полную группу событий, имеем равенствоp + q = 1.
Например, вероятность безаварийной работы нового двигателя на втором году эксплуатации P(A) = 0.9 , вероятность безаварийной работы нового двигателя на третьем году эксплуатации P(S1) = 0.7
.

Если рассматривать эти события как независимые, то вероятность безаварийной работы двигателя на третьем году эксплуатации
при безаварийной работе на втором году составляет

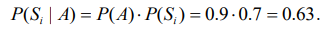
Вероятность варианта, при котором на втором году эксплуатации была поломка
двигателя, а третий год прошел без аварий составляет

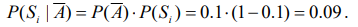
Обращаем внимание, что после ремонта двигателя вероятность поломки следует рассчитать по данным второй строки табл.1 (двигатель после ремонта).

Вариант 1. Новый автобус.
При анализе эксплуатации нового автобуса в течение 3-х лет необходимо
рассмотреть разные варианты, которые могут сложиться в зависимости от надежности работы его двигателя. При этом следует использовать понятие сложного события и его
вероятности. Следует также помнить, что на первом году эксплуатации поломка.
нового двигателя практически исключена. В зависимости от надежности работы двигателя на 2-м и 3-м году эксплуатации возможны 4 варианта эксплуатации:

1. БР2+БР3. Двигатель служит без ремонта в течение трех лет эксплуатации. Вероятность такого варианта составляет P1=0.9 х 0.7=0.63. Расходы при этом варианте равны 300 х 3 = 900 тыс. долларов.
2. БР2+Р3. Второй год без ремонта, третий год – ремонт. Вероятность такого
варианту составляет P2 = 0.9 х 0.3 = 0.27. Расходы при данном варианте составляют 300 х 3 + 40 = 940 тыс. долларов.
3. Р2+БР3. Ремонт на втором году и безремонтный третий год. Вероятность
такого варианта составляет P3=0.1 х 0.9=0.09. Расходы при данном варианте составляют 300 х 3 + 40 = 940 тыс. долларов.
4. Р2+Р3. Ремонт на втором году и замена двигателя на третьем году.
Вероятность такого варианта составляет P4=0.1 х 0.1=0.01. Затраты при
данном варианте составляют 300 х 3+40+100=1040 тыс. долларов. Обращаем
внимание, поскольку повторный ремонт двигателя не рекомендуется, на третьем году необходимо установить новый двигатель.
Средневероятные затраты трехлетней эксплуатации составляют:
Z = P1 x Z1 + P2 x Z2 + P3 x Z3 + P4 x Z4 = 0.63 x 900 + 0.27 x 940 + 0.09 x 940 + 0.01 х 1040 = 567.0 + 253.8 + 84.6 + 10.4 = 915.8 (тыс. долларов.)
Ожидаемый доход составляет 700 х 3 = 2100 тыс. долларов.
Ожидаемая прибыль составляет 2100 – 915,8 = 1184,2 тыс. долларов.
Итак, как показали расчеты, ожидаемая прибыль от эксплуатации нового автобуса за 3 года составляет 1184.2 тыс. долларов.

Вариант 2. Автобус, бывший в употреблении.
Эксплуатация двигателя автобуса, который уже был в использовании, приравнивается к эксплуатации двигателя после первого ремонта. Поэтому уже после первой
Поломки такого двигателя необходимо устанавливать в новый двигатель. После замены
двигателя, двигатель считается новым и вероятность его поломки рассчитывается с
использованием первой строчки табл. 1. Вероятность безотказной работы такого
двигателя на первом году эксплуатации составляет 0.9, на втором году – 0.7, на
третьем году – 0.4. За первоначальный капитал 300 тыс. долларов. можно купить 2 автобуса БВ. При анализе эксплуатации автобуса БВ в течение 3-х лет необходимо
рассмотреть разные варианты, которые могут сложиться в зависимости от надежности работы двигателя (табл. 1). Всего возможны 8 вариантов эксплуатации:
1. БР1+БР2+БР3. Двигатель служит без ремонта в течение трех лет эксплуатации. Вероятность такого варианта составляет P1 = 0.9 х 0.7 х 0.4 = 0.252. Затраты при этом варианте равны 450 х 3 = 1350 тыс. долларов.
2. БР1+БР2+Р3. Первый и второй год без ремонта, третий год – ремонт (замена двигателя). Вероятность такого варианта составляет P2 = 0.9 х 0.7 х 0.6=0.378. Затраты при этом варианте равны 450 х 3 + 100 = 1450
тыс. долларов.
3. БР1+Р2+БР3. Ремонт на 2-м году и безремонтные 1-ый и 3-й годы. Вероятность такого варианта составляет P3 = 0.9 х 0.3 х 1 = 0.27. Затраты при
этом варианте равны 450 х 3 + 100 = 1450 тыс. долларов.

Обращаем внимание на то, что вероятность поломки двигателя на третьму году равен нулю, поскольку двигатель перед этим был заменен.
4. БР1+Р2+Р3. Ремонт на 2-м году и поломка на 3-м году. Вероятность
такого варианта равна нулю (вероятность поломки двигателя на третьем году равна нулю, поскольку двигатель перед этим был заменен) P4 = 0.9 х 0.3 х 0 = 0.
5. Р1+БР2+БР3. Замена двигателя на первом году и безремонтные 2-й и 3-й
годы. Вероятность такого варианта составляет P5 = 0.1 х 1 х 0.9 = 0.09. Затраты при этом варианте равны 450 х 3 + 100 = 1450 тыс. долларов.
6. Р1+БР2+Р3. Замена двигателя на первом году и ремонт на третьем году.
Вероятность такого варианта составляет P6 = 0.1 х 1 х 0.1 = 0.01. Расходы
при этом варианте равны 450 х 3 + 40 + 100 = 1490 тыс. долларов.
7. Р1+Р2+БР3. Замена двигателя на первом году и ремонт двигателя на 2-м
году. Вероятность такого варианта составляет 0. P7 = 0.
8. Р1+Р2+Р3. Вероятность данного варианта также нулевая. P8=0.
Средневероятные затраты трехлетней эксплуатации составляют:
Z = P1 x Z1 + P2 x Z2 + P3 x Z3 + P4 x Z4 + P5 x ​​Z5 + P6 x Z6 + P7 x Z7 + P8 x
Z8 = 0.252 x 1350 + 0.378 x 1450 + 0.270 x 1450 + 0.000 x 1490 + 0.090 x 1450 +
0.010 x 1490 + 0.000 x 1550 + 0.000 x 1650 = 340.2 + 548.1 + 391.5 + 130.5 + 14.9
= 1425.2 (тыс. долларов.)
Ожидаемый доход составляет 700 х 3 х 2 = 4200 тыс. долларов.
Ожидаемая прибыль составляет (2100 – 1425.2) х2 = 1349.6 тыс. долларов.

Вывод. Второй вариант бизнес-плана более выгоден.

4. Задача о выдаче кредита.

Бизнесмен просит банк о кредите $15 000. Банк принимает решение по двум альтернативам:
1. Выдать кредит под 15% годовых. Статистика свидетельствует, что 4% таких кредитов не возвращаются (последняя строчка таблицы 1).
2. Вложить эти деньги ($15 000) в другой бизнес-проект с гарантированным возвратом под 9% годовых.
3. Перед выдачей кредита можно проверить кредитоспособность клиента в аудиторской фирме. Это стоит $80.
Статистика ранее выданных кредитов приведена в следующей таблице 3.1.

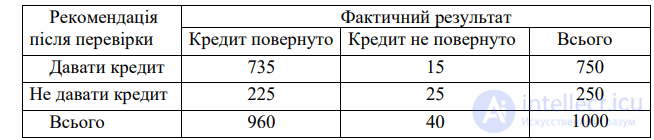
Таблица 3.1. Статистика выданных кредитов

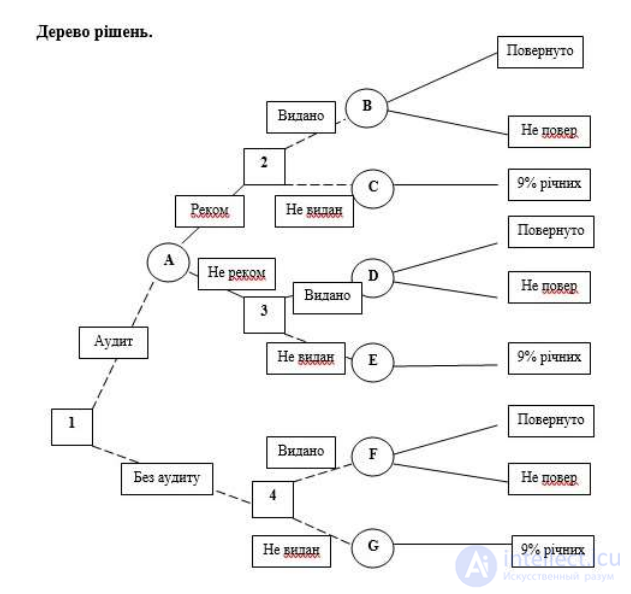
формирование деревьев решений. Построим дерево решений. Пунктирные линии
соединяют квадраты возможных решений. Сплошные полосы соединяют круги вероятных результатов. Квадратные узлы обозначают моменты принятия решений. Круглые узлы обозначают полученные результаты. Для каждой ветки дерева необходимо просчитать его вероятность и ожидаемый финансовый результат.
Расчет вероятностей. Сначала рассчитаем вероятности всех вариантов, используя статистические данные.
1. Фирма рекомендовала, кредит возвращен. Р=735/750=0.98.
2. Фирма рекомендовала, кредит не возвращен. Р=15/750=0.02.
3. Фирма не рекомендовала, кредит возвращен. Р=225/250=0.90.
4. Фирма не рекомендовала, кредит не возвращен. Р=25/250=0.10.

Анализ дерева решений.
1. Сначала рассмотрим ветки В и С, являющиеся последствиями решения 2 (Рекомендовать выдать кредит).
Доход при результате В: (15 000 + 2 250) х 0.98 – 15 000 х 0.02 = 16 605.
Чистый доход: 16 605 – 15 000 = 1 605.
Доход при результате С: (15000 + 1350) х 1.00 = 16350.
Чистый доход: 16 350 – 15 000 = 1 350.
Следовательно, находясь в квадрате 2, следует выбрать вариант В, поскольку он имеет больший ожидаемый доход. Итак, принимаем решение: вариант С отклонить (перечеркнуть ветку). Квадрату 2 присвоить ожидаемый доход 1605.

2. Теперь рассмотрим ветки D и E, являющиеся последствиями решения 3.
Доход при итоге D: 17 250 х 0.90 – 15 000 х 0.10 = 14 025.
Чистый доход: 14 025 – 15 000 = -975.
Доход при результате E: 16350.
Чистый доход: 16 350 – 15 000 = 1 350.

Следовательно, находясь в квадрате 3, следует выбрать вариант Е, поскольку он имеет больший ожидаемый доход. Итак, принимаем решение: вариант D отклонить (перечеркнуть ветку). Квадрату 3 присвоить ожидаемый доход 1350.
1. Теперь рассмотрим ветки F и G, являющиеся следствием решения 4 (без аудита).
Доход при результате F: 17 250 х 0.96 – 15 000 х 0.04 = 15 960.
Чистый доход: 15 960 – 15 000 = 960.
Доход при результате G: 16350.
Чистый доход: 16 350 – 15 000 = 1 350.
Следовательно, находясь в квадрате 4, следует выбрать вариант G, поскольку он имеет больший ожидаемый доход. Итак, принимаем решение: вариант F отклонить (перечеркнуть ветку). Квадрату 4 присвоить ожидаемый доход 1 350.
2. Теперь рассмотрим узлы А и 4. Рассчитаем математическое ожидание для
варианту А: 1 605 х 0.75 + 1 350 х .25 = 1 541.25
Чистый доход: 1541.25 – 80 = 1461.25.

Следовательно, находясь в квадрате 1, следует выбрать вариант А, поскольку он имеет больший ожидаемый доход, чем вариант 4 (1 461.25 > 1 350). Итак, принимаем решение: вариант 4 отклонить (перечеркнуть ветку). Квадрату 1 присвоить ожидаемый доход 1 461.25.
3. Строим оптимальный путь по дереву решений: 1 – А – (если аудитор рекомендует, то выдать ссуду, иначе не выдавать, а инвестировать в другой проект)

структурная избыточность

Структурно-топологические характеристики систем описывают их организацию и взаимосвязи между компонентами. Одной из важных характеристик является структурная избыточность.

Структурная избыточность представляет собой наличие дополнительных элементов или связей в системе, которые не являются строго необходимыми для ее функционирования, но обеспечивают определенную устойчивость и способность к работе даже при частичных сбоях или повреждениях.

Примеры структурной избыточности могут быть найдены в различных областях:

1. Информационная технология: В компьютерных сетях часто используется структурная избыточность, например, в виде резервирования сетевых линий, чтобы в случае отказа одной линии обеспечивалась непрерывность связи.

2. Транспортные системы: В системах общественного транспорта наличие дополнительных маршрутов или средств передвижения позволяет избежать полного паралича системы при возникновении сбоев на каком-либо участке.

3. Электроэнергетика: В энергосистемах может быть использована структурная избыточность путем создания резервных источников энергии или запасных сетей для сглаживания нагрузок и компенсации отказов.

4. Биология и медицина: В организмах человека и животных также присутствует структурная избыточность. Например, иммунная система содержит различные механизмы обороны, которые могут активироваться при различных угрозах.

Структурная избыточность

Структурный параметр, отражающий превышение общего числа связей над минимально необходимым, будем называть структурной избыточностью R. Она определяется следующим образом:

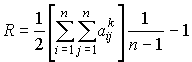(2)

Данная характеристика используется для косвенной оценки экономичности и надежности исследуемых ВС. Для систем с максимальной избыточностью, имеющих структуру типа "полный граф" 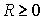; для систем с минимальной избыточностью R=0; для несвязных систем 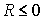. Таким образом, система с большим R потенциально более надежна. Ее целесообразно дополнить другим параметром, учитывающим неравномерность связей .

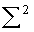Равномерное распределение связей в структуре неориентированного графа имеющего, m ребер и n вершин, характеризуется средней степенью вершины 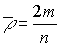. Тогда, введя понятие отклонения где 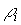- действительная степень i- й вершины заданного графа, можно определить квадратичное отклонение заданного распределения степеней вершины от равномерного:

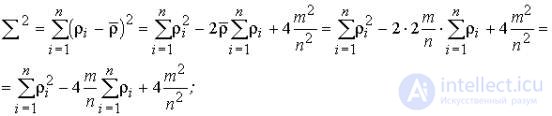(3)

Показатель 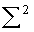характеризует недоиспользованные возможности заданной структуры, имеющей m ребер и n вершин, в достижении максимальной связности.

Закон избыточности частей системы

Закон избыточности частей системы предусматривает, что приблизительно 20% функций, элементов и связей системы выполняют около 80% работы. При создании работоспособной системы нужно учитывать, что для выполнения какой-либо работы, кроме основных элементов и связей (выполняющих главную функцию), необходимо еще приблизительно 80% вспомогательных, причем они, как правило, выполняют только 20% основной работы. Учитывая это, следует предусмотреть "лишний" расход вещества, энергии и информации (приблизительно 20% на обеспечение главной функции и 80% основных и вспомогательных).

ИЗБЫТОЧНОСТЬ может быть функциональная и структурная.

Функциональная избыточность определяется тем, что для обеспечения работоспособности системы, помимо главной функции, необходимо выполнять еще основные и вспомогательные функции.

Структурная избыточность определяется необходимостью введения дополнительных элементов и связей, кроме рабочего органа. Для обеспечения работоспособности системы; необходимы дополнительно: трансмиссия, источник и преобразователь энергии (двигатель), система управления и корпус.

19. Структурно – топологические характеристики систем.

При проведении анализа системы целесообразно оценить количественно качество структуры системы и ее элементов с позиций общесистемного подхода.

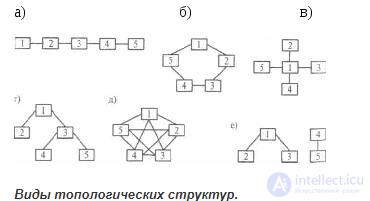
Виды топологических структур.

Виды топологических структур рассмотрим на примере пяти элементов.


. Виды топологических структур: а) последовательная структура; б) кольцевая структура; в) радиальная структура; г) древовидная структура; д) структура типа полный граф; е) несвязная структура
Связность структуры. Данная характеристика позволяет выделить наличие обрывов, висячие вершины и т. д. Для неориентированных графов связность всех элементов в структуре соответствует выполнению условия:



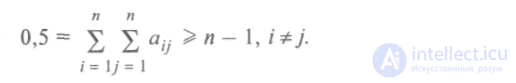
В соотношении (4.6) — элемент матрицы смежности. Правая часть (4.6) определяет необходимое минимальное число связей в структуре неориентированного графа, содержащего п вершин. Коэффициент 0,5 берется в силу того, что одна и та же связь д. и а учитывается дважды.

Соотношение (4.6) можно переписать в виде



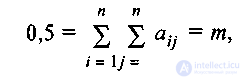
т.е. это не что иное, как число ребер в неориентированном графе. Определим т как функцию от п для основных типов структур в общем виде.

Последовательная структура. Очевидно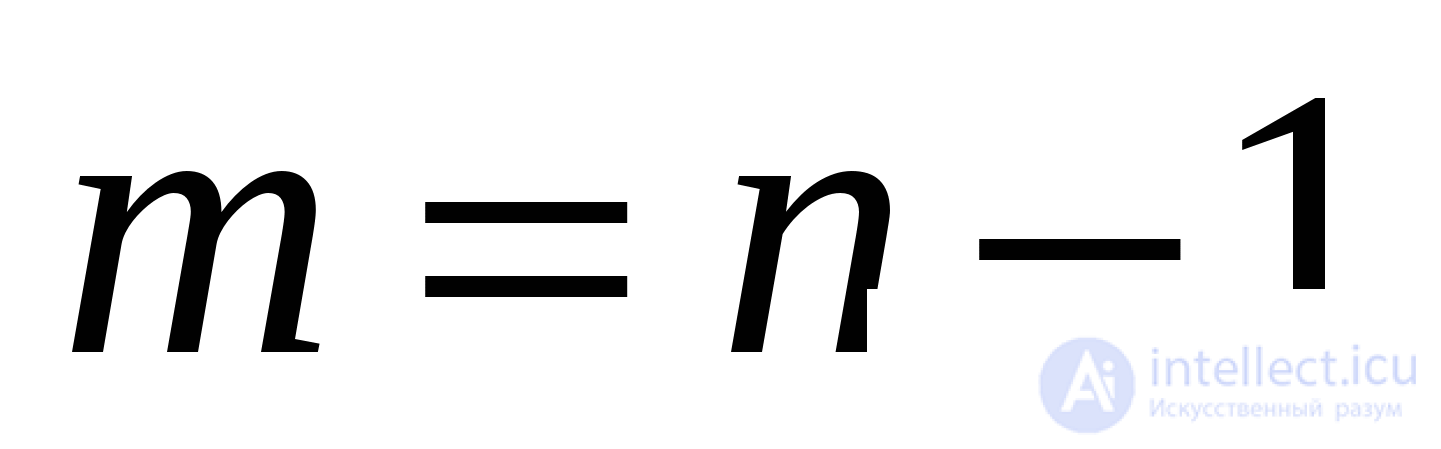

Кольцевая структура. Очевидно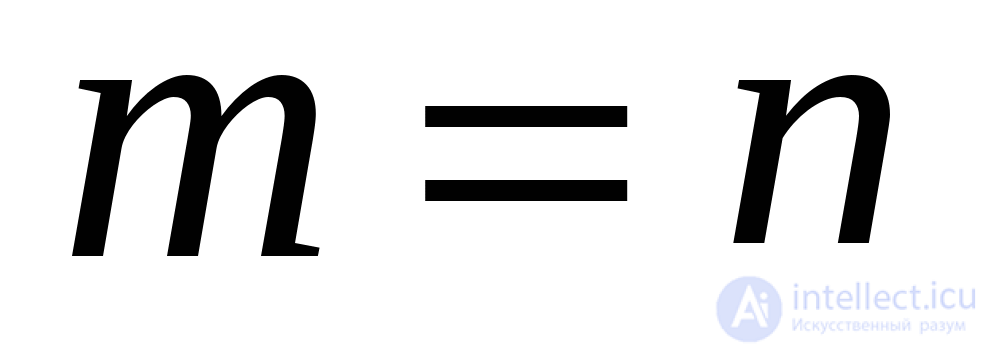

Радиальная структура. Очевидно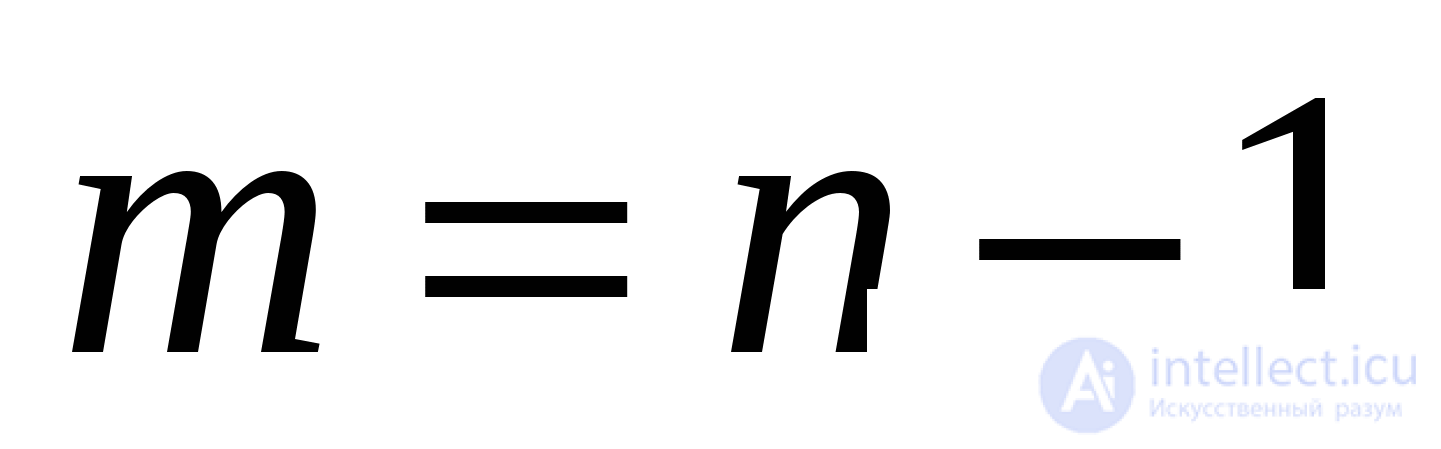

Древовидная структура. Трудно сказать в общем виде, так как параметр определяется видом дерева.

Структура полный граф. Для первого элемента число связей n-1, так как он связан со всеми элементами, кроме себя. У второго элемента n-2 связей, т.к. нет связи с самим собой,

и связь с первым мы уже учли. Аналогично у третьего — n-3 ит. д. У последнего — 0. так как все связи учтены. Итак, имеем



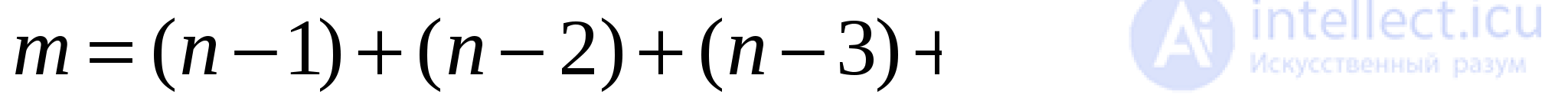
Для несвязной структуры эта характеристика не имеет смысла.

Структурная избыточность. Это структурный параметр, отражающий превышение общего числа связей над необходимым минимальным числом связей. Разделим в соотношении (4.6) все члены на n-1и разность обозначим через R. Тогда будем иметь



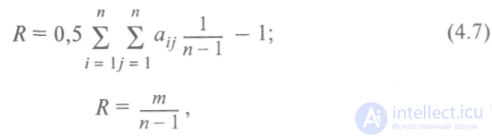
Где R - структурная избыточность.

Найдем структурную избыточность для рассмотренных типовых структур в общем виде, учитывая ранее найденную зависимость т = т(n).



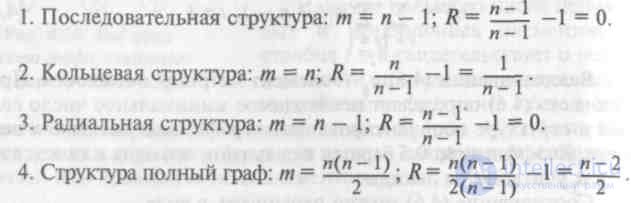
Данная структурная характеристика используется для косвенной оценки экономичности и надежности исследуемой системы. Для систем с избыточностью — R > О, для систем с минимальной избыточностью - R = О, для несвязных систем — R < 0.

Структурная компактность.

Для ее оценки вводится параметр, отображающий близость элементов между собой. Близость 2-х элементов i u j определяется через минимальную длину пути для ориентированного графа (цепи — для неориентированного) — _. Тогда сумма всех минимальных путей (цепей) между всеми элементами отражает обитую структурную близость элементов в анализируемой структуре. Обозначим эту величину через Q и, в соответствии с определением, будем иметь:

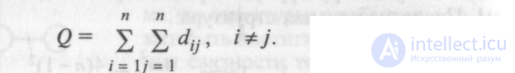
Степень централизации структуры.

1. Наименее «централизованными» и наиболее «размытыми» с этих позиций являются структуры кольцевая и полный граф, в которых элементы нагружены абсолютно одинаково. Для этих двух структур структурная компактность



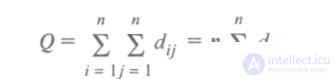
где 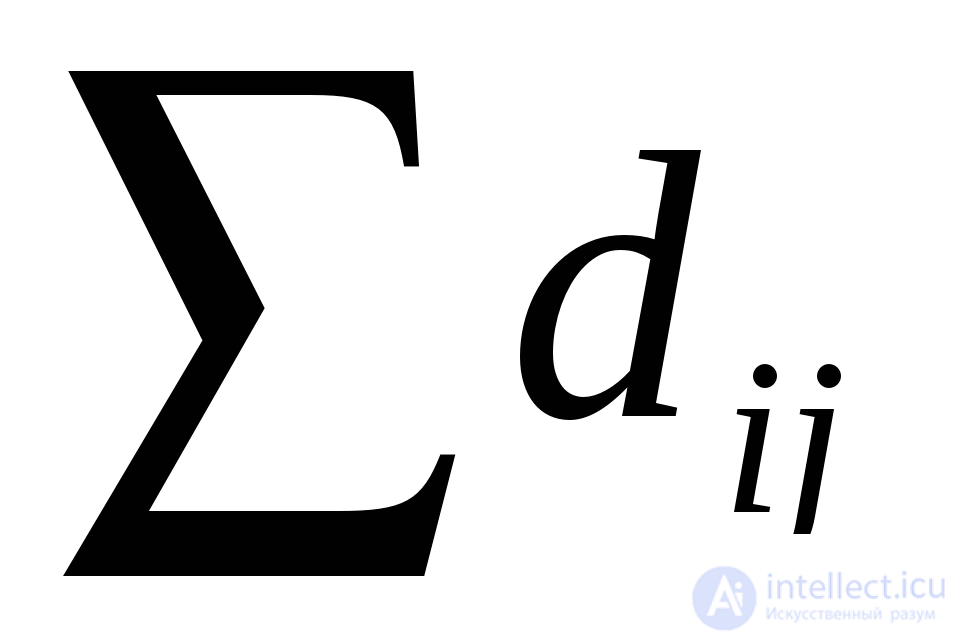— сумма расстояний от j-того элемента до всех остальных.

2. Но, с другой стороны, чем более компактна структура, тем легче центру управлять ею. Поэтому введем новый параметр (У, выражаемый через 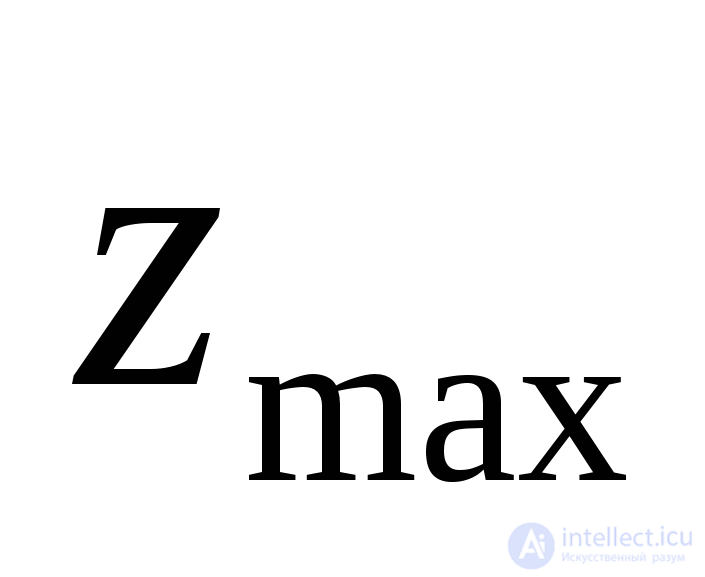и возрастающий с ростом компактности.

Введем понятие индекса центральности, определив его как



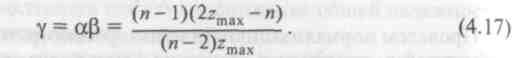
Для структур с максимальной степенью централизации (радиальная) 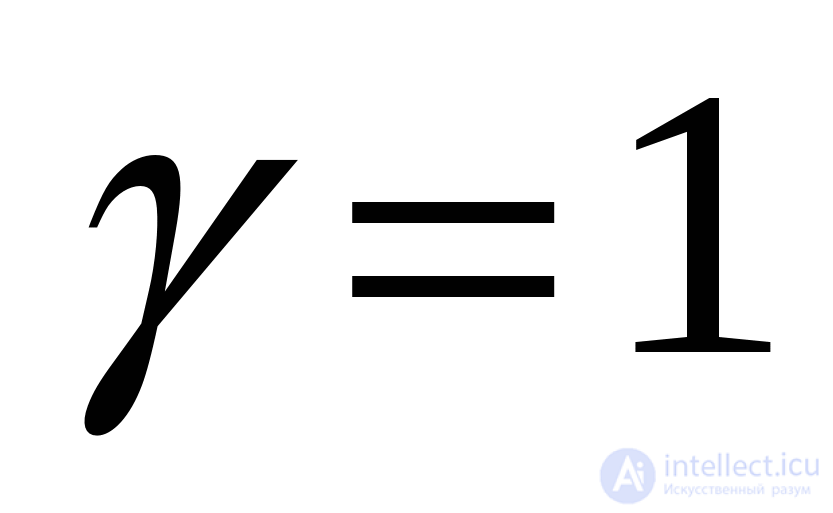, для структур с равномерным распределением связей (кольцевая и полный граф)_.

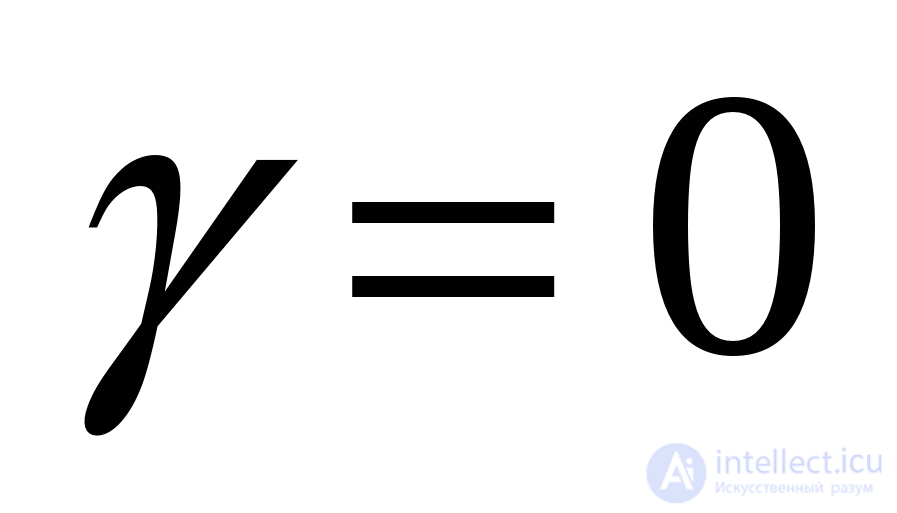Сравнительный анализ топологических структур. Результаты вычисления топологических характеристик для типовых структур (для случая 5-ти элементов) сведены в таблицу 4.16. Для древовидной структуры расчеты произведем непосредственно исходя из определений параметров.


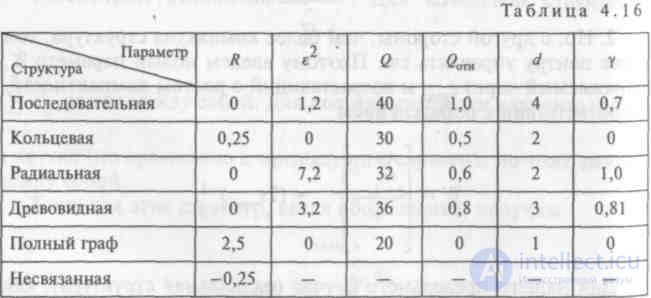
Анализ табл. 4.16 показывает следующее.

1. Для несвязных структур структурная избыточность R<0, для структур без избыточности (последовательная, радиальная, древовидная) R=0; для структур с избыточностью по связям (кольцевая, полный граф) R>0

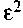2. Структуры (последовательная, радиальная, древовидная) с R=0 различаются по показателю, наибольшую неравномерность связей имеет радиальная структура.
3. Наибольшую близость элементов (показатель ) имеет структура типа полный граф, наименьшую — последовательная.

4. Радиальная и древовидная структуры, имеющие одинаковые или близкие значения 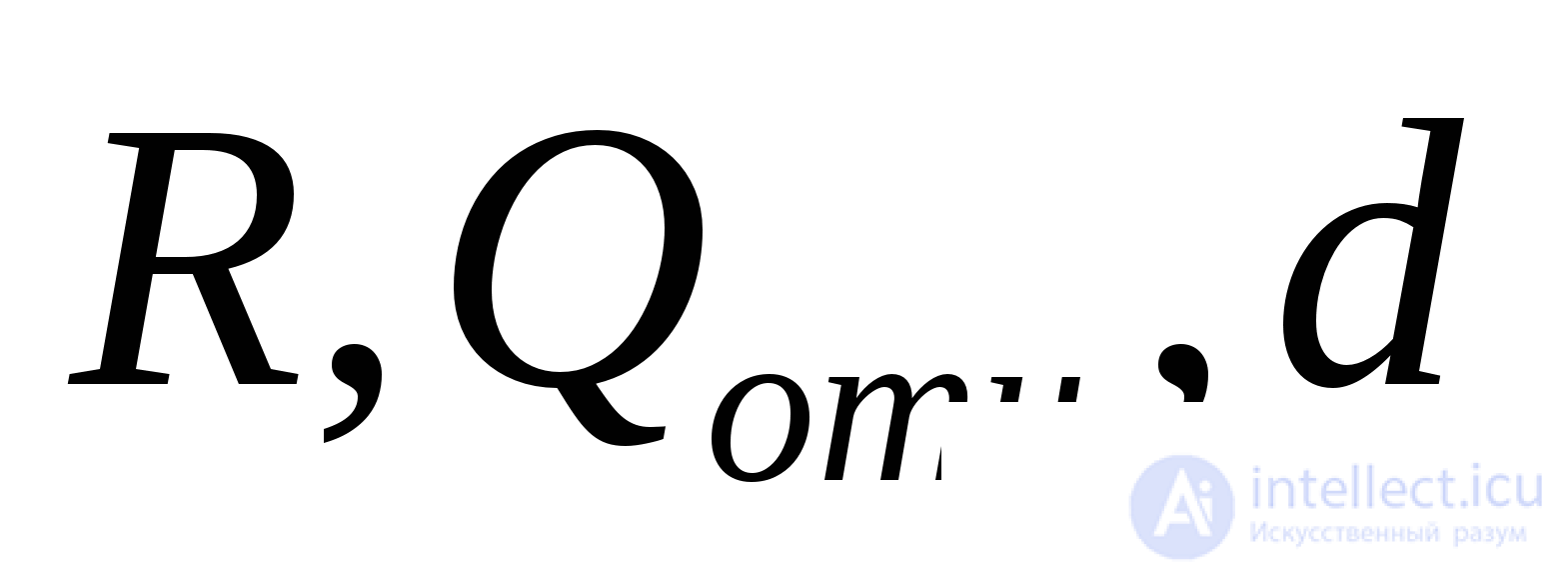, значительно отличаются по показателям 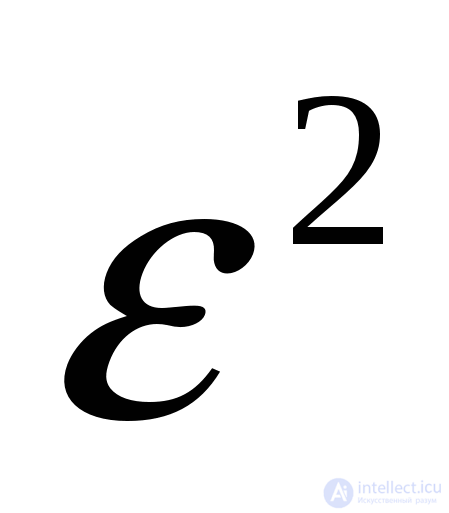и 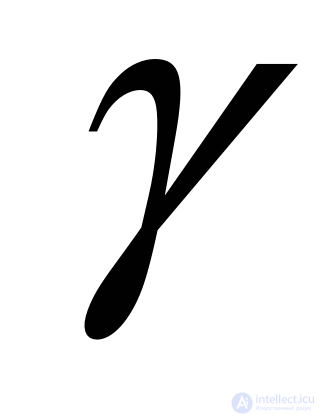, что соответствует физическому
смыслу, ибо отход от полной централизации в структуре ведет к большей равномерности распределения связей по элементам.

Рассмотренные выше структурные характеристики были получены только на основе информации о составе элементов и их связях. Дальнейшее развитие методологии структурных параметров для решения задач структурного анализа может быть основано на учете неструктурной информации за счет введения числовых функций на графах. Это позволяет, наряду с составом элементов и направленностью их взаимодействия, учитывать при решении задач другие стороны их функционирования (временные, надежностные, стоимостные и т. п.)

Рассмотрим далее третий уровень формализации задач структурного анализа, когда учитывается состав сигналов взаимосвязи элементов и их вид. Напомним, что на первом уровне учитывалось лишь наличие связи между элементами, на втором - наличие и направление этой связи.

Структурная избыточность помогает системе обеспечивать стабильность и устойчивость в условиях изменчивости, несовершенства и внешних воздействий. Она может способствовать более надежной работе системы и повышению ее жизнеспособности.

Выводы из данной статьи про структурный анализ указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое структурный анализ, структурная избыточность и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Системный анализ (системная философия, теория систем)

Продолжение:

Часть 1 Структурный анализ, Структурно – топологические характеристики систем. Структурная избыточность
Часть 2 Структурная избыточность - Структурный анализ, Структурно – топологические характеристики систем.