Лекция
Привет, мой друг, тебе интересно узнать все про стоячие волны в линиях передачи, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое стоячие волны в линиях передачи , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
В линии без потерь поглощаемая приемником, активная мощность равна нулю.
Это возможно в случаях:
Онлайн демонстрация и симуляция работы Несогласованные линии передачи (стоячая волна):
Открыть на весь экран Несогласованные линии передачи (стоячая волна)
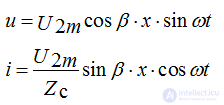
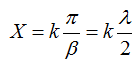


Стоячие волны и резонанс
Всегда, когда есть несоотвествие между сопротивлением линии передачи и нагрузкой, происходит отражение. Если падающий сигнал имеет одну частоту, то этот сигнал будет накладываться на отраженные волны, и возникнет стоячая волна.
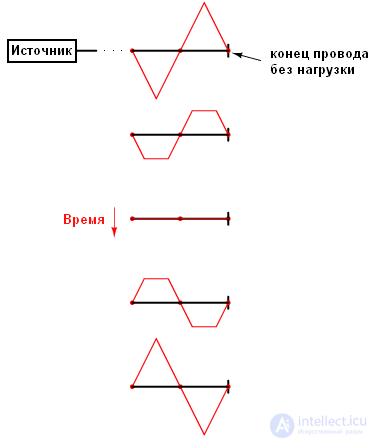
На рисунке показано, как треугольная падающая волна зеркально отражается от открытого конца линии. Для простоты, линия передачи в этом примере показана как единая жирная линия, а не как пара проводов. Падающая волна идет слева направо, а отраженная – справа налево.

Если мы сложим эти два сигнала, то увидим что третий, стационарный сигнал, создается по всей длине линии: красная линия на рисунке ниже – сумма падающей и отраженной волн:
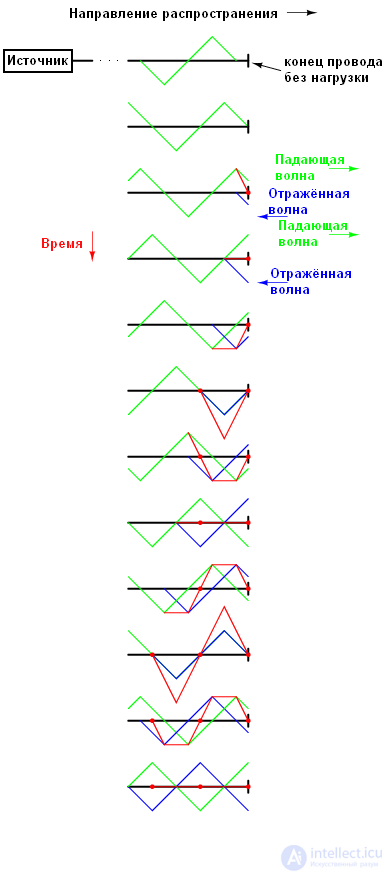
Эта третья волна является суммой падающей и отраженной волны. Она не распространяется по кабелю, как падающая или отраженная волна. Обратите внимание на точки вдоль линии, где падающая и отраженная волна всегда гасят друг друга: эти точки никогда не меняют позицию.
Стоячие волны распространены и в физическом мире. Рассмотрим веревку, привязанную за один конец, и потрясем ее:
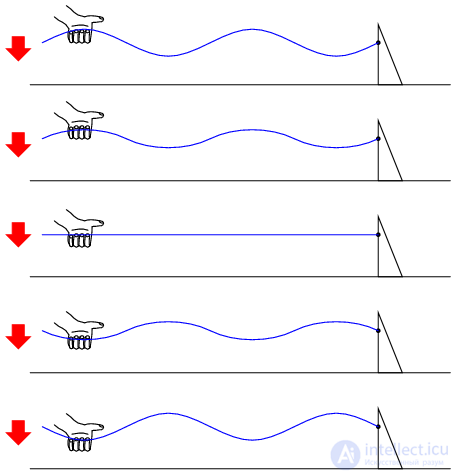
Узлы (с точками где нет вибрации) и пучности (точки максимальной вибрации) остаются неизменными по всей длине веревки. Струнные инструменты также создают стоячую волну, с узлами максимальной и минимальной вибрации вдоль их длины. Основное отличие между веревкой и струнным инструментом в том, что инструмент уже настроен на правильную частоту вибрации:

Ветер, дующий через открытые трубы, также производит стоячие волны. В этом случае, колеблются молекулы воздуха в трубе, а не твердое тело. Стоячая волна может заканчиваться в узле (минимальная амплитуда) или в пучности(максимальная амплитуда) и это зависит от того, открыт или закрыт другой конец трубки:

Закрытый конец трубы создает узел, а открытый – пучность. По аналогии, якорь струны – это узел, а свободный конец (если он есть) – пучность.
Обратите внимание, что внутри трубы могут возникать стоячие волны разных частот. Есть несколько резонансных частот для любой системы, поддерживающей стоячие волны.
Более высокие частоты должны быть кратны базовой частоте.
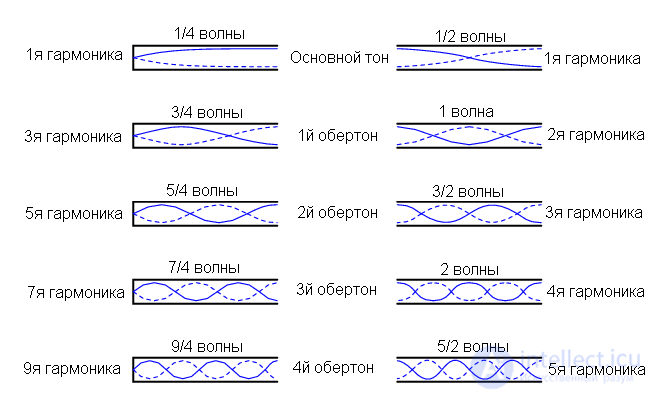
Фактические частоты для любой из этих гармоник (обертонов) зависят от физического размера трубы и скорости распространения волн (в данном случае — скорости распространения звука).
В линиях связи также возможно создать стоячие волны, и их частота будет зависеть от типа нагрузки на конце линии, от скорости распространения и физической длины. Резонанс в линиях передачи более сложен, чем резонанс струн или воздуха в трубах, потому что мы должны учитывать напряжение и ток волн.
Резонанс в линиях передачи легче понять, используя компьютерное моделирование. Для начала, рассмотрим согласованную линию на 75 Ом:
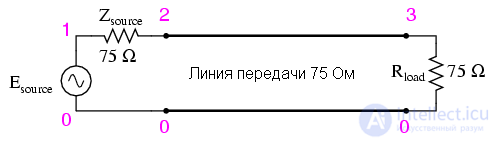
Используя SPICE для имитации схемы, мы укажем для линии T1 волновое сопротивление 75 Ом(z0 = 75) и задержку распространения 1 мкс. Это удобный способ для выражения физической длины линии передачи – количество времени на распространение сигнала. Для реального кабеля RG-59B/U это будет длина 198 метров. 1 мкс соответствует частоте 1МГц. Я буду выбирать частоты от нуля до этой частоты, чтобы показать, как система реагирует на разные частоты.
Вот SPICE модель:

Выполним это моделирование и построим график падения напряжения на сопротивлении источника (Zsource) – это будет индикатор тока, и график напряжения на конце линии (напряжение на нагрузке). Мы увидим, что источник напряжения – на графике показано как vm(1) (величина напряжения между узлом 1 и точкой заземления 0) ровно 1 Вольт. Напряжения в точке 2 и 3 будут 0,5Вольт. Напряжение на резисторе – как индикатор тока – будет 0,5 Вольт:
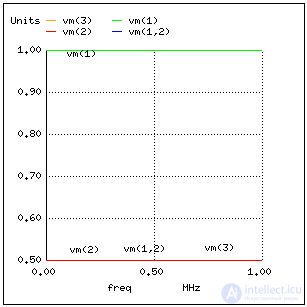
В системе, где все сопротивления идеально согласованы, не может быть никаких стоячих волн, и нет резонансов на графике Боде.
Теперь давайте изменим сопротивление на 999 МОм, чтобы имитировать открытую линию передачи. Мы определенно должны получить отраженные волны на каких то частотах, от 1мГц до 1МГц:
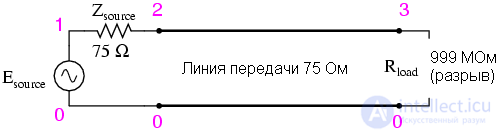

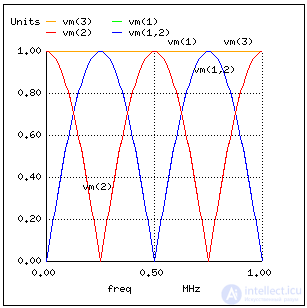
Здесь напряжение питания линии vm(1) и напряжение на нагрузке остаются на прежнем уровне – 1Вольт. Другие падения напряжения зависят от частоты(так же от 1мГц до 1 МГц). Есть пять примечательных частот вдоль горизонтальной линии: 0Гц, 250кГц, 500кГц, 750кГц, 1МГц. Изучим каждую точку с учетом напряжения и тока в различных точках схемы.
• 0Гц (на самом деле 1мГц) – сигнал практически постоянного тока, и цепь ведет себя так же, как если бы было подано 1Вольт постоянного тока. Ток не течет, так как указано нулевое падение напряжения на резисторе Zsource, график vm(1,2), и напряжение на источнике равно напряжение в конце линии vm(2) (напряжение между точкой 2 и точкой 0).

• На 250кГц мы видим нулевое напряжение в точке 2, максимальный ток от источника и полное напряжение на конце линии.
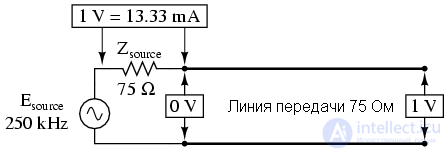
Вы можете быть удивлены, как это может быть? Как мы можем получить полное напряжение на открытом конце линии, если на входе нулевое напряжение? Ответ можно найти в парадоксе стоячей волны. На частоте 250кГц длина линии точно равна ¼ длины волны. Так как конец линии разомкнут, то не может быть никакого тока, но напряжение – будет. Таким образом, на конце провода будет узел для тока (ток равен нулю) и пучность для напряжения(максимальная амплитуда):

• На частоте 500кГц в линию укладывается ровно половина волны, и здесь мы видим еще одну точку в которой ток равен нулю, а напряжение вновь имеет полную амплитуду:
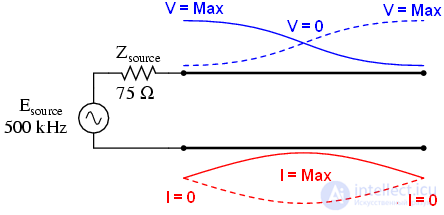
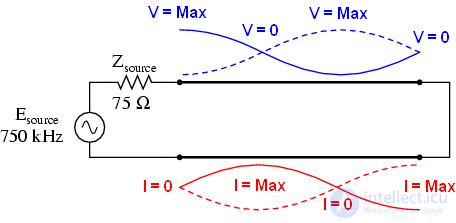
• На частоте 750 кГц картина похожа на частоту 250кГц: напряжение на источнике равно нулю, и максимальный ток. ¾ волны укладывается в линии, в результате чего источник видит короткое замыкание в точке подключения к линии передачи даже не смотря на то, что на другом конце линии обрыв:
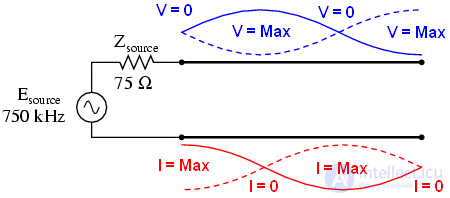
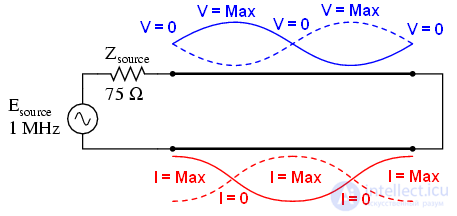
• Когда частота доходит до 1МГц, в линии укладывается один полный период волны. На данный момент, и ток, и напряжение в начале линии равны таковым в конце линии. И если в конце линии ток равен нулю (сопротивление равно 999 МОм), то и в начале линии ток тоже равен нулю. Напряжение на источнике равно напряжению на нагрузке. Фактически, источник видит разомкнутую цепь.

Аналогично короткое замыкание на конце линии генерирует стоячие волны, хотя узлы и пучности по току и напряжению меняются местами: На короткозамкнутом конце линии не будет напряжения (узел), но будет максимальный ток (пучность). Далее идет моделирование SPICE и иллюстрации того, что происходит на всех интересных частотах: 0Гц, 250 кГц, 500кГц, 750кГц, 1 МГц. Короткое замыкание моделируется сопротивлением нагрузки 0 мкОм.




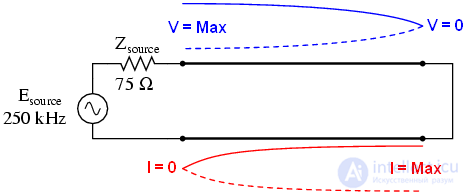
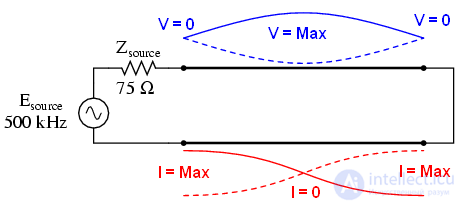
В обоих примерах(разомкнутая и короткозамкнутая линия) отражается вся энергия. Об этом говорит сайт https://intellect.icu . 100 процентов падающей волны достигает конца линии и отражается обратно к источнику. Если, однако, линия передачи нагружена каким-то сопротивлением, будет разница между максимальными и минимальными значениями напряжения и тока вдоль линии.
Предположим, что мы нагрузили линию резистором 100 Ом вместо 75:

Построим модель для этого случая:


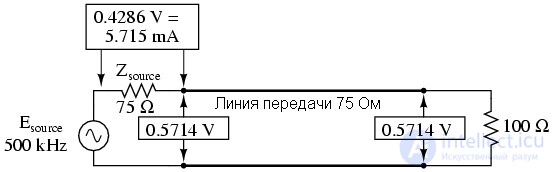
Если мы запустим другой SPICE анализ с выводом текстовых значений вместо графика мы можем обнаружить, что все интересные частоты остались теми же самими (Постоянный ток, 250кГц, 500кГц, 750кГц, и 1МГц):


На всех частотах напряжение на источнике в точке 1 равно 1Вольт, как и положено. Напряжение на нагрузке также остается постоянным, но имеет меньшую амплитуду (0,5714 Вольт). Однако, напряжение питания линии (точка 2, график v(2)) и ток (график v(1,2)) указывает, что ток от источника меняется в зависимости от частоты.


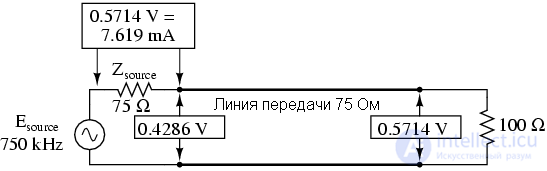

На нечетных гармониках основной частоты(250кГц и 750кГц) мы видим разные уровни напряжения в начале и конце линии, поскольку на этих частотах стоячие волны создают узел с одной стороны линии и пучность – с другой. В отличие от разомкнутой и короткозамкнутой линии, максимальные значения не достигают ни нуля, ни 100% от исходного сигнала. Но мы все так же имеем точки с минимумом и максимумом напряжения. То же самое справедливо и для тока. Если нагрузочное сопротивление линии не соответствует волновому сопротивлению линии, мы будем иметь точки максимального и минимального тока на некоторых фиксированных точках линии передачи, соответствующие узлам и пучностям.
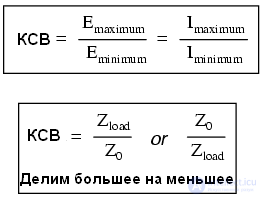
Один из способов выражения уровня стоячих волн – отношение максимальной амплитуды (в точке пучности) к минимальной амплитуде для напряжения или тока. Это отношение называется КСВ – коэффициент стоячей волны. Если на линии обрыв или короткое замыкание, то КСВ равен бесконечности, так как минимальная амплитуда будет равна нулю. В примере 75 Ом линии с нагрузкой 100 Ом КСВ будет равен 1,333: максимальное напряжение линии на 250 или 750кГц(0,5714 В) деленное на минимальное напряжение линии (0,4286 В).
КСВ также можно рассчитать, зная нагрузочное сопротивление и волновое сопротивление линии, делением большего значения на меньшее. В нашем примере 100Ω /75Ω = 1,333.
Линия с идеально согласованной нагрузкой будет иметь КСВ равный 1. Это считается идеалом не только из-за того, что отраженные волны – это энергия не достигшая нагрузки, но из-за высоких значений напряжения и тока: высокое напряжение может создать пробой в изоляции, а высокий ток повредить проводники.
Также, линия с плохим КСВ выступает в качестве антенны. Это нежелательно: такая антенна может навести помехи на близлежащие провода. Интересно, что антенны – это открытые линии передач, и работают они при КСВ как можно ближе к 1. Это значит, что вся энергия излучается.
Следующая фотография показывает точку соединения в линии связи радиопередатчика. Большие медные трубы с керамическим изолятором представляют из себя жесткую коаксиальную линию с волновым сопротивлением 50 Ом.

Гибкий коаксиальный кабель с волновым сопротивлением 50 Ом. Белая пластиковая труба соединяет газ внутри труб: они запечатаны для защиты от влаги. Обратите внимание на плоские провода для соединения линий. Почему они не круглые? Это сделано из-за скин-эффекта, который делает бесполезной большую площадь поперечного сечения на больших частотах.
Как и многие линии связи, они работают на низком КСВ. Как мы увидим в следующем разделе, явление стоячих волн в линиях связи не всегда вредны, так как они могут быть использованы для полезной функции: преобразования импеданса.
Преобразование импеданса
Стоячие волны в резонансных точках короткозамкнутых или открытых линиях могут производить необычные эффекты. При длине линии ½ длины волны (и в кратное число раз больше) источник видит нагрузку как есть. На следующих иллюстрациях это показано:
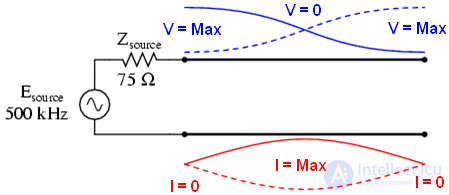
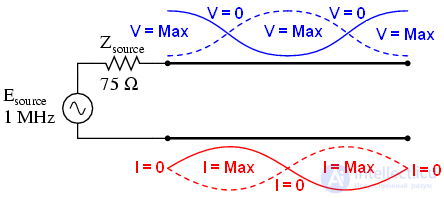
В обоих случаях на концах линии пучность для напряжения и узел для тока. Линия имитирует нагрузку – бесконечное сопротивление, источник видит обрыв.
То же верно, если на линии короткое замыкание: в точке подключения источника будет минимум напряжения и максимум тока.
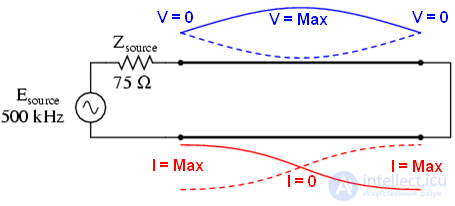

Однако, если длина линии равна четверти длины волны, источник при коротком замыкании на конце линии увидит обрыв, а оборванную линию будет видеть как короткозамкнутую.
Линия разомкнута, а источник видит короткое замыкание:

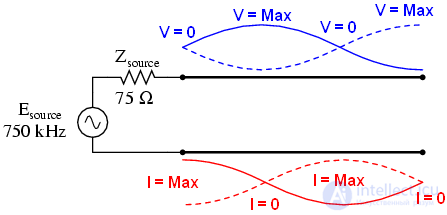
Линия замкнута, а источник видит обрыв:
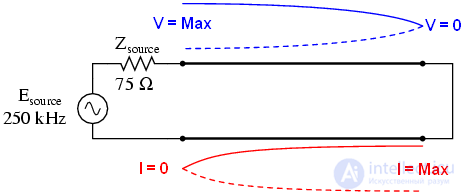
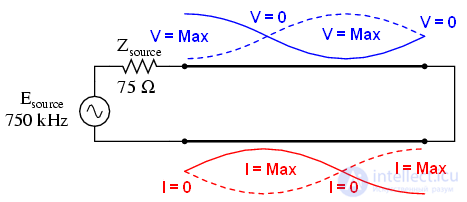
На этих частотах линия передачи ведет себя как трансформатор сопротивления, превращая бесконечное сопротивление в нуль и наоборот. Это происходит только в резонансных точках, когда в линию укладывается четверть волны и кратно больше(3/4, 5/4, 7/4, 9/4 …), но если частота известна и неизменна, то это явление может быть использовано для согласования разных волновых сопротивлений друг с другом.
Возьмем в качестве примера линию передачи 75Ω с нагрузкой 100Ω. Из численного моделирования SPICE определим какое сопротивление видит источник:

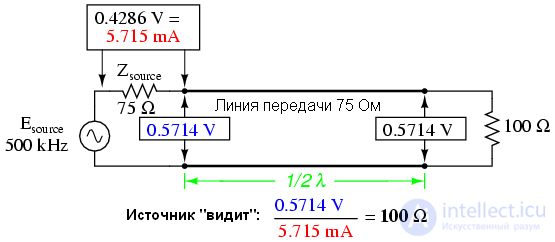

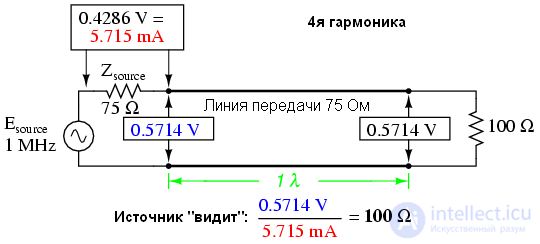
Простое уравнение связывает волновое сопротивление линии(Z0), импеданс нагрузки(Zload) и входной импеданс(Zinput) для несогласованной линии на нечетной гармоники:
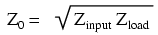
Рассмотрим практический пример, когда надо согласовать нагрузку 300Ω и источник 75Ω. Все, что нам нужно сделать, так это вычислить правильное волновое сопротивление линии и длину для четверти длины волны на 50МГц.
Во-первых, рассчитаем сопротивление линии. Z0 = Sqrt(75*300) = 150Ω.
Во-вторых, надо рассчитать длину линии. Предположим, коэффициент укорочения 0,85, скорость света 300 тысяч км/сек, скорость сигнала будет 255 тысяч км/сек. Делим эту скорость на частоту сигнала и получаем длину волны 5,1 метр. Нам нужно четверть длину волны – это будет 1,275м.
Вот схема для SPICE анализа:

Мы можем указать длину линии по задержке сигнала. При частоте 50МГц период будет 20нс. Время задержки на четверть длины волны будет 5нс.


На частоте 50МГц в точке 1-2 падает ровно половина – 0,5В, а вторая половина напряжения падает на линии связи в цепи 2-0. Это означает, что источник видит в нагрузке 75Ω. Нагрузка, однако, получает не половину, а 1 Вольт (напряжение v(3)). На сопротивлении 75Ω падает 0,5В или 3,333мВт – столько же, сколько и на нагрузке 300 Ом при напряжении 1В. В соответствии с теоремой максимальной мощности (теоремой Якоби) на нагрузке рассеивается максимальная возможная мощность. Линия передачи длиной в четверть волны, волновым сопротивлением 150Ω и нагрузкой 300Ω ведет себя как 75Ωнагрузка.
Конечно, это все будет работать лишь на 50МГц и нечетных гармониках. Для других частот линию передачи придется удлинять или укорачивать.
Как ни странно, линия той же длины будет согласовывать 300Ω источник и 75Ω нагрузку. Это показывает, что явление преобразования импеданса в корне отличается от принципа работы трансформатора с двумя обмотками.


В этом случае на внутреннем сопротивлении источника упадет 0,5В, или 833мкВт. На нагрузке будет 0,25В – те же 833мкВт.
Этот метод часто используется для согласования линий передачи и антенны в радиопередачиках, так как там частота часто известна и неизменна. Минимальная длина преобразователь импеданса соответствует ¼ длины волны.
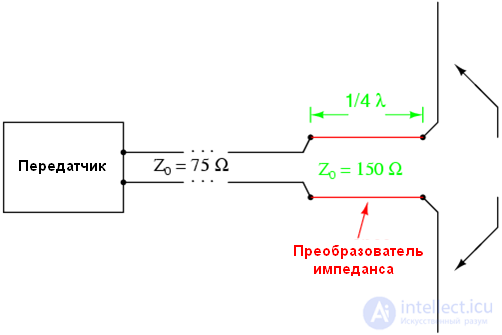
Линии передачи по своим параметрам аналогичны колебательным контурам, но в отличие от них параметры линии передачи (L - индуктивность проводников, C- емкость между проводниками, R - активное сопротивление проводников, G- проводимость диэлектрика линии) не являются сосредоточенными, а равномерно распределены по всей длине линии. Параметры L и С характеризуют резонансные свойства линии, а параметры R и G характеризуют потери (затухание) в ней.
В зависимости от характера и величины сопротивления нагрузки линии, линия передачи может работать в режимах бегущей волны, стоячей волны или в смешанном режиме.
Режим бегущей волны возникает, когда сопротивление нагрузки Zn и волновое сопротивление линии Zo равны и отражения от конца линии не возникает.
Стоячие волны возникают в линии передачи, если ее волновое сопротивление Zo не равно сопротивлению нагрузки Zn. Рассмотрим сначала предельные ситуации в линии передачи, когда линия разомкнута либо замкнута накоротко.
Если линия на конце замкнута накоротко (Zn =0) или разомкнута ( Zn = бесконечности), то вся поступающая энергия отражается от конца линии и возвращается ко входу.
Рассмотрим случай, когда линия разомкнута на конце, т. е. когда нагрузочное сопротивление бесконечно велико. Бегущая волна, дойдя до конца разомкнутой линии, отражается и двигается обратно к генератору. Таким образом, в линии распространяются две бегущие волны: одна — падающая — движется от генератора к концу линии, а другая — отраженная — движется в обратном направлении. В результате взаимодействия падающих и отраженных волн в линии образуются стоячие волны. Эти волны проявляются наличием в линии максимумов (пучностей) напряжения и тока, а также их нулевых значений (узлов), сдвинутых по фазе относительно друг друга.
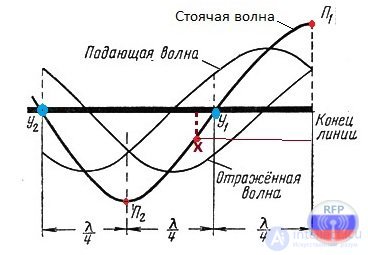
На рис.1 показано сложение падающей и отраженной волн напряжения, для некоторого момента времени, в разомкнутой линии.
Здесь П1, П2 – пучности напряжения, У1, У2 – узлы напряжения, Х- любая точка волны на расстоянии Х от конца линии.
Аналогично получается график и для стоячей волны тока, но пучности тока в ней сдвинуты на 90* относительно пучностей напряжения.
Значения напряжения стоячей волны в каждой точке Х от конца линии определяется уравнением: u =2Um Cos 2?x/? Cos ?t. И соответственно для волны тока:
i = 2Im Sin2?x/? Sin ?t. Здесь Um, Im - амплитуды напряжения и тока бегущей либо отраженной волны. Эти уравнения называют уравнениями стоячей волны.
Из этих уравнений видно, что в каждой точке стоячей волны и напряжения, и тока происходят колебания и напряжения, и тока той же частоты, что и в падающих и отраженных волнах.
Причем, если зафиксировать некоторую точку, которая имеет координату Х, то для значения напряжения или тока в этой точке получим уравнение колебания амплитуды напряжения или тока: Ux = |2Um Cos 2?x/?|; Ix =|2 Im Sin2?x/?|.
Отсюда видно, амплитуда напряжения и тока стоячей волны зависит от координаты Х. Знак модуля означает, что значение амплитуды – всегда положительно.
Как возникает стоячая волна и что она из себя представляет, можно наглядно проследить кликнув по картинке:
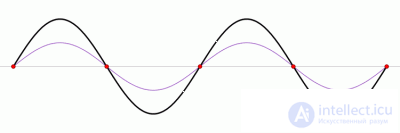 Стоячая волна (черная линия ), возникает в результате сложения двух волн, падающей и отраженной (красная и синяя линии), распространяющихся во встречных направлениях. Красные точки обозначают узлы — точки или области в пространстве, в которых амплитуда колебательного процесса минимальна и равна разности амплитуд падающей и отраженной волн (амплитуда стоячей волны в узлах равна нулю). Посередине между каждой парой соседних узлов располагается пучность — точка или область в пространстве, в которой амплитуда стоячей волны максимальна и равна сумме амплитуд падающей и отраженной волн. Фаза колебательного процесса стоячей волны при переходе через узел меняется на 180°.
Стоячая волна (черная линия ), возникает в результате сложения двух волн, падающей и отраженной (красная и синяя линии), распространяющихся во встречных направлениях. Красные точки обозначают узлы — точки или области в пространстве, в которых амплитуда колебательного процесса минимальна и равна разности амплитуд падающей и отраженной волн (амплитуда стоячей волны в узлах равна нулю). Посередине между каждой парой соседних узлов располагается пучность — точка или область в пространстве, в которой амплитуда стоячей волны максимальна и равна сумме амплитуд падающей и отраженной волн. Фаза колебательного процесса стоячей волны при переходе через узел меняется на 180°.
Характер распределения напряжения или тока вдоль линии при стоячей волне не изменяется с течением времени. В разные моменты времени изменяется только величина напряжения или тока в каждой точке линии.
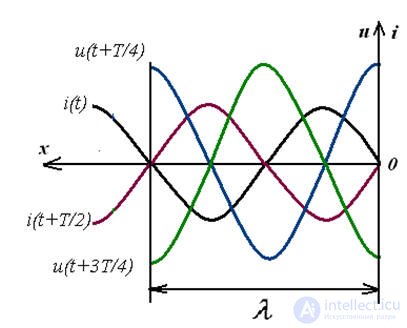
На рис.2 показано распределение напряжения вдоль разомкнутой линии для нескольких различных моментов времени на протяжении нескольких полупериодов.
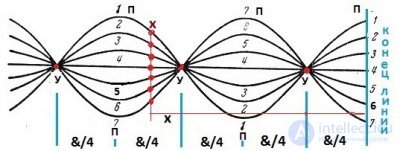
Кривая 1 соответствует фазе, когда напряжение в линии наибольшее. Далее напряжение становится все меньше и меньше (кривые 2 и 3). Затем напряжение во всей линии становится равным нулю (прямая 4). Затем оно меняет знак и начинает возрастать (кривые 5 и 6). Через полпериода после начала процесса напряжение снова достигает амплитудного значения (кривая 7), но с обратным знаком. В каждой точке Х линии напряжение колеблется по синусоидальному закону, причем мгновенные значения напряжения этого колебания (амплитуды для этих точек) для разных точек различны. Для пучностей амплитуда наибольшая, равная двойной амплитуде бегущей волны, для других точек она меньше, и, наконец, для узлов она равна нулю.
Все сказанное относится и к току. Но в стоячей волне узлы тока получаются там, где пучности напряжения, а пучности тока находятся в узлах напряжения. Иначе говоря, стоячая волна тока сдвинута на 1/4(&-лямбда) или 90 градусов относительно стоячей волны напряжения. Графически это изображено на рис.3 двумя кривыми. Кривая тока дана сплошной линией, а кривая напряжения — штрихом.

Амплитуда напряжения в пучности Uпуч, равная двойной амплитуде напряжения бегущей волны 2Um, а амплитуда тока в пучности Iпуч, равна двойному значению амплитуды тока бегущей волны 2Im. Отношение этих величин есть волновое сопротивление Zo линии:

Так как амплитуды напряжения и тока в стоячей волне величины положительные, на графиках часто их откладывают в положительной области. На рис.4 представлены графики распределения напряжения и тока стоячих волн в короткозамкнутой линии (рис.4а) и разомкнутой линии (рис.4б)
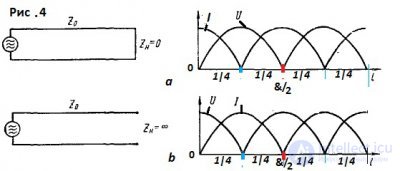
В каждом случае сопротивление, как в каждой точке линии, так и на ее концах, определяется отношением напряжения к току – U/I. Вследствие разности фаз между током и напряжением, линия передачи характеризуется не только активным сопротивлением, но и реактивным, которое может быть индуктивным (XL) или емкостным ( Xc) в зависимости от знака фазового сдвига .
Сдвиг фаз на 90° между током и напряжением при стоячей волне показывает, что в линии происходит колебание энергии, сходное с колебательным процессом в замкнутом контуре. Когда напряжение в линии наибольшее, а ток равен нулю, то вся энергия сосредоточена в электрическом поле. Через четверть периода напряжение равно нулю, а ток имеет наибольшее значение и вся энергия сосредоточена в магнитном поле. Еще через четверть периода энергия снова возвратится в электрическое поле и процесс колебания энергии повторится.
На рис.4а по графику видно, что на конце линии, замкнутой накоротко, (начало координат) ток имеет максимальное значение (пучность тока), а напряжение равно нулю, т.к. сопротивление нагрузки равно нулю (Zn=0).
Начиная же с закороченного конца линии начинает возрастать индуктивная составляющая импеданса - XL, которая достигает наибольшего значения на расстоянии 1/4 & (&-лямбда) от конца линии. Но здесь ей противостоит столь же большая емкостная составляющая импеданса - Xc, возникающая в следующем участке 1\4 & длины линии. На расстоянии &/4 от конца закороченной линии, линия представляет собой параллельный контур, а параллельно включенные индуктивная и емкостная составляющие импеданса равны (XL= Xc), и полное сопротивление линии в этой точке становится чисто активным.
На отрезке линии между &/4 и &/2 емкостная составляющая импеданса уменьшается до нуля и в точке &/2 импеданс снова становится чисто активным. В этой точке линия представляет собой последовательный колебательный контур. Далее ход импеданса повторяется и в зависимости от своей длины короткозамкнутая двухпроводная линия передачи (фидер) настраивается или как индуктивность, или как емкость подобно последовательному либо параллельному резонансному контуру.
Сходным образом ведет себя и разомкнутая двухпроводная линия. Рис.4b.
В этом случае соотношения импеданса сдвинуты на 90 градусов относительно короткозамкнутого режима (рис.4а). Открытому концу линии (на графике начало координат) соответствует бесконечно большое емкостное сопротивление, спадающее до нуля через 1/4 & длины линии. В этой точке линия ведет себя как последовательный резонансный контур с чисто активным полным сопротивлением. Между точками &/4 и &/2 импеданс носит индуктивный характер, а при &/2 устанавливается режим параллельного резонанса и т.д.
Эти свойства двухпроводной линии (фидера) позволяют использовать их как резонансные элементы в колебательных контурах, фильтрах, согласующих устройствах и пр. Отрезки линии, представляющие собой эквиваленты индуктивности, емкости или колебательного контура, могут иметь длину менее &/4. Это позволяет подбором длины линии получить необходимую индуктивность или емкость. Например, нужную индуктивность можно получить из короткозамкнутой линии длиной меньше &/4, а из разомкнутой линии длиной менее &/4 можно получить необходимую емкость. Замкнутая линия длиной &/4 представляет собой параллельный колебательный контур, а эта же разомкнутая линия превратится в последовательный колебательный контур.
На рис.5 представлены разные возможности использования короткозамкнутой или разомкнутой линии в качестве согласующего элемента.
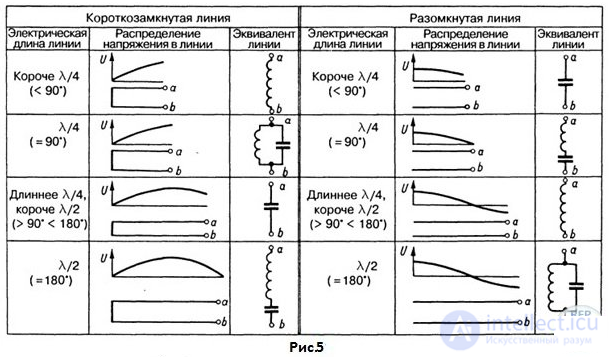
Холостой ход (линия разомкнута) и короткое замыкание являются предельными ситуациями в линии передачи.
Когда сопротивление нагрузки линии Zn больше нуля или меньше бесконечности, но не равно волновому сопротивлению линии Zo, падающая волна частично отражается от конца линии и в ней устанавливается режим смешанных волн, но амплитуда отраженной волны будет меньше, чем в случае короткозамкнутой или разомкнутой линии.
В случае, когда сопротивление нагрузки Zn больше Zo, напряжение максимально на нагрузке и в точках, отстоящих от конца линии на кратное число полуволн, как и в случае линии, разомкнутой на конце. В тех же самых точках будут минимумы тока, а максимумы тока находятся в точках, отстоящих от конца линии на нечетное число четвертей волн, рис. 6a.
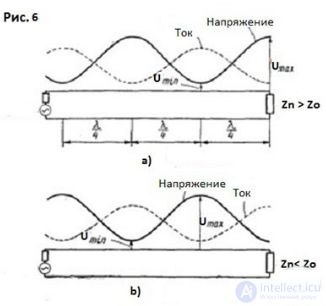
Если же Zn < Zo, максимумы напряжения будут находиться, как и в замкнутой линии, в точках, отстоящих от конца линии на нечетное число четвертей волн, в тех же точках будут минимумы тока, рис. 6b.
Линии передачи могут быть как произвольной длины (не настроенные), так и настроенные. Линию передачи называют настроенной, если ее электрическая длина равна нечетному числу четвертей волн (четвертьволновый трансформатор) или целому числу полуволн (полуволновый повторитель). Несмотря на наличие стоячих волн в таких настроенных линиях, их входные и полные выходные сопротивления являются активными (чисто омическими), они являются только переносчиками импеданса и не влияют на резонансную частоту антенны. Настроенную линию передачи допустимо рассматривать как неизлучающее продолжение антенны.
Если же линия передачи не настроенная (произвольной длины) и Z n не равно Zo (несогласованная), в линии наряду с бегущими волнами возникают стоячие волны (смешанный режим), появляется реактивность, которая может быть индуктивной (XL) или емкостной ( Xc) в зависимости от длины линии (знака фазового сдвига между током и напряжением ).
Антенна, как и линия передачи, так же представляет собой резонансный контур с распределенными параметрами. Рис.7.
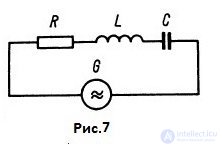
Распрямленный проводник также обладает индуктивностью и емкостью, которые распределены по всей его длине. Когда проводник находится в резонансе с возбуждающей частотой, его можно рассматривать как колебательный контур. К примеру, эквивалентная схема полуволнового вибратора представляет собой последовательный резонансный контур. Рис.7.
Несогласованные линии передачи произвольной длины, вследствие возникновения в них стоячих волн, добавляют реактивность в антенную систему антенна-фидер, резонансная частота которой может быть сдвинута вверх или вниз по частоте, в зависимости от знака реактивности (XL или Xc) на конце линии, подключаемой к антенне.
Линии передачи, работающие в режиме стоячей волны, имеют бОльшие потери, чем линии, работающие в режиме бегущей волны. Это объясняется тем, что в режиме стоячей волны в пучностях тока увеличиваются омические потери в проводниках, а в пучностях напряжения увеличиваются диэлектрические потери в диэлектрике линии передачи.
Понравилась статья про стоячие волны в линиях передачи? Откомментируйте её Надеюсь, что теперь ты понял что такое стоячие волны в линиях передачи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Комментарии
Оставить комментарий
Электротехника, Схемотехника, Аналоговые устройства
Термины: Электротехника, Схемотехника, Аналоговые устройства