Привет, мой друг, тебе интересно узнать все про применение комплексных чисел для расчета электрических цепей, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
применение комплексных чисел для расчета электрических цепей , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
Расчет электрических цепей с использованием тригонометрических функций весьма сложен и громоздок, поэтому при расчете электрических цепей синусоидального тока используют математический аппарат комплексных чисел.
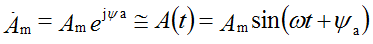
Модуль комплексной амплитуды равен амплитуде синусоидальной величины, а аргумент – ее начальной фазе.
Вводится понятие комплексного величин амплитуд и действующих значений тока, напряжения, ЭДС и т.д.
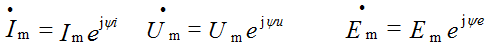
Комплексные действующие значения пропорциональны комплексным амплитудам и записываются в виде:
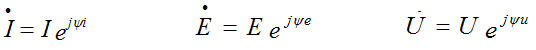
Синусоидальные электрические величины, представленные в комплексной форме, можно изображать графически. На комплексной плоскости в системе координат с осями +1 и +j, которыми обозначены положительные действительная и мнимая полуоси, строятся комплексные векторы. Длина вектора пропорциональна модулю действующих значений. Угловое положение вектора определяется аргументом комплексного числа. При этом отсчет положительного угла ведется против часовой стрелки от положительной действительной полуоси. Комплексная плоскость разбивается на четыре четверти:
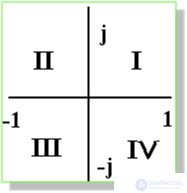
Итак, рассмотрим нашу тригонометрическую функцию A(t) представленную в виде комплексной величины на комплексной плоскости. Об этом говорит сайт https://intellect.icu . Получается, что наша функция представлена в виде вектора вращающегося на комплексной плоскости против часовой стрелки со скоростью ω, как показано на рис.1.
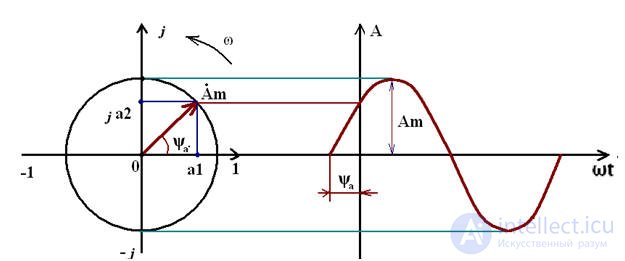
Рис.1
Из рис.1 видно, что вектор на комплексной плоскости можно построить двумя способами, первый, зная размер вектора и угол, и второй способ, зная координаты вектора по действительной и мнимой осям.
Первый способ это показательная форма представления комплексного числа, т.е.
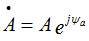
где - комплексная величина, А - модуль комплексного числа или действующее значение величины, ψа - аргумент комплексного числа
Второй способ алгебраическая форма представления комплексного числа:
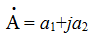
где а1 = Асоs ψа а2 = Аsin ψа
Правила перехода из одной формы в другую.
Переход из показательной формы в алгебраическую форму:
дано
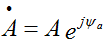
Используется формула Эйлера
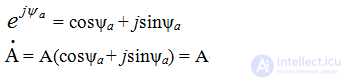
Переход из алгебраической формы в показательную форму:
дано
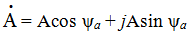
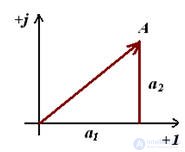
Рис. 2
Из рис.2 видно, вектор образует с осью координат прямоугольный треугольник, поэтому воспользуемся теоремой Пифагора, и найдем размер вектора, который равен гипотенузе треугольника:
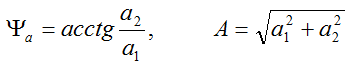
причем особое внимание уделим углу – аргументу ψа модуля комплексного числа:
если вектор находится во второй и третьей четвертях комплексной плоскости, то к полученному значению аргумента необходимо прибавить 180° или π.
Если а1 = 0, то комплексное число называется мнимым, аргумент ψа = ± 90°
Если а2 = 0, то комплексное число называется действительным, ψа = 0, ± π
Простейшие математические операции с комплексными числами
Простейшие математические операции такие, как сложение, вычитание, умножение и деление проводятся с комплексными числами следующим образом: сложение и вычитание удобно проводить в алгебраической форме, а умножение и деление в показательной.
Единичные комплексы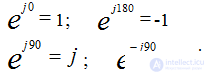 действия с j
действия с j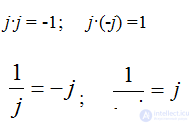
Понравилась статья про применение комплексных чисел для расчета электрических цепей? Откомментируйте её Надеюсь, что теперь ты понял что такое применение комплексных чисел для расчета электрических цепей
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Электротехника, Схемотехника, Аналоговые устройства
Из статьи мы узнали кратко, но содержательно про применение комплексных чисел для расчета электрических цепей
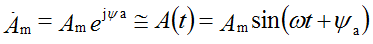
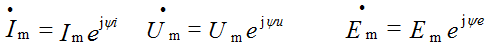
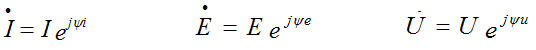


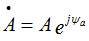
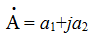
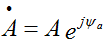
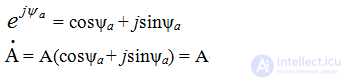
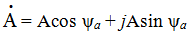

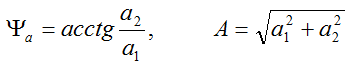
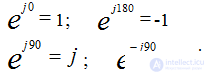
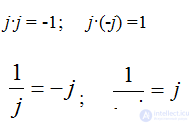
Комментарии
Оставить комментарий
Электротехника, Схемотехника, Аналоговые устройства
Термины: Электротехника, Схемотехника, Аналоговые устройства