Постквантовая криптография. основы и алгоритмы

Привет, Вы узнаете о том , что такое постквантовая криптография, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое постквантовая криптография, криптография , настоятельно рекомендую прочитать все из категории Криптография и криптоанализ, Стеганография и Стегоанализ.

постквантовая криптография — часть криптографии, которая остается актуальной и при появлении квантовых компьютеров и квантовых атак. Так как по скорости вычисления традиционных криптографических алгоритмов квантовые компьютеры значительно превосходят классические компьютерные архитектуры, современные криптографические системы становятся потенциально уязвимыми для криптографических атак. Большинство традиционных криптосистем опирается на проблемы факторизации целых чисел или задачи дискретного логарифмирования, которые будут легко разрешимы на достаточно больших квантовых компьютерах, использующих алгоритм Шора. Многие криптографы в настоящее время ведут разработку алгоритмов, независимых от квантовых вычислений, то есть устойчивых к квантовым атакам.

Существуют классические криптосистемы, которые опираются на вычислительно сложные задачи и имеют ряд существенных отличий от систем указанных выше, из-за чего их гораздо сложнее решить. Эти системы независимы от квантовых вычислений, и, следовательно, их считают квантово-устойчивыми (quantum-resistant), или «постквантовыми» криптосистемами.

Постквантовая криптография в свою очередь отличается от квантовой криптографии, которая занимается методами защиты коммуникаций, основанных на принципах квантовой физики.

1. Основы криптографии ( повторение)

Что такое криптография и для чего она вообще нужна? Скажем, Алиса и Боб хотят обменяться сообщением, да так, чтобы его содержание оставалось в секрете. Очевидно, что у каждой из сторон должен быть свой ключ. И на этом этапе можно выделить два подвида криптосистем.

К первому из них относятся симметричные криптосистемы. Здесь один ключ может быть легко вычислен из другого, а зачастую они и вовсе совпадают. Значимыми плюсами таких криптосистем являются простота реализации и высокая скорость работы за счет использования более простых операций. Однако, если один из ключей будет скомпрометирован, всякая попытка защитить секретную информацию потеряет свой смысл.

Такая проблема изящно решается в асимметричных криптосистемах с помощью специальных алгоритмов. Однако тут мы сталкиваемся с трудоемкостью операций, что может быть неэффективно для большого объема данных. В таких криптосистемах нужно очень постараться, чтобы из одного ключа вычислить другой, и, пока чей-то компьютер не обладает огромной мощью темной стороны, можно быть относительно спокойными за секретность защищаемых данных.

Интересная многоходовочка… Ну а как она реализуется, спросит пытливый %username%? Все дело в так называемых односторонних функциях. Пусть есть функция y=f(x). По известному аргументу x вычислить значение функции y проще, чем захватить Вестерос с тремя драконами и армией безупречных. Однако вычисление аргумента x по известному значению функции y является довольно-таки трудоемкой задачей.

Наиболее известными кандидатами в односторонние функции являются задача факторизации числа, которая состоит в разложении числа на простые множители, и задача дискретного логарифмирования, которая заключается в поиске неизвестного k по известным значениям y и g, которые удовлетворяют: y=gk. Первая, например, применяется в широко известной криптосистеме RSA, а вторую можно встретить в схеме установления ключа Диффи-Хэллмана.

Однако с учетом стремительного, как полет дракона, роста производительности вычислительных устройств, возникает необходимость в увеличении длины ключа, ну а это может стать критическим фактором для устройств с ограниченной мощностью…Эх, было бы так здорово, появись такая структура, которая бы позволила сократить размер ключа при таком же уровне стойкости… И, к счастью, она существует! Название сему чуду – эллиптическая кривая.

2 Введение в постквантовую криптографию и закат RSA

RSA, эллиптические кривые, квантовый компьютер, изогении… На первый взгляд, эти слова напоминают какие-то заклинания, но все куда проще сложнее, чем кажется!

Необходимость перехода к криптографии, устойчивой к атаке на квантовом компьютере, уже официально анонсирована NIST и NSA, из чего вывод довольно-таки простой: пора вылезать из зоны комфорта!

А значит, стоит отходить от старой доброй RSA и даже, вероятно, от полюбившихся многим эллиптических кривых и узнавать новые, не менее интересные примитивы, способные обезопасить конфиденциальную информацию.

Чтобы разобраться в тонкостях криптографии на эллиптических кривых, проследить новомодные веяния постквантовой криптографии и даже прикоснуться к ней с помощью библиотеки Microsoft SIDH, добро пожаловать под кат, %username%!

3. Введение в использование эллиптических кривых

Эллиптическая кривая — над полем — неособая кубическая кривая на проективной плоскости над (алгебраическим замыканием поля ), задаваемая уравнением 3-й степени с коэффициентами из поля и «точкой на бесконечности».

. Неособой ее называют, потому что ко всем ее точкам можно однозначно провести касательную. Ну раз это кривая кубическая, то и задаваться она должна уравнением третьей степени, которое в обобщенной форме Вейерштрасса выглядит следующим образом:

y2+a1xy+a3y=x3+a2x2+a4x+a6

Однако на практике такую форму кривой можно встретить нечасто. Различают формы Лежандра, Монтгомери, Гессе и т.д. Использование той или иной формы может увеличить эффективность операций над точками эллиптической кривой. Например, в форме Монтгомери есть возможность выполнять умножение точки на число за фиксированное время благодаря алгоритму лестницы Монтгомери.

Наверняка многие сталкивались с формой Вейерштрасса, ее называют канонической для полей с характеристикой charK≠2,3:

E(K):y2=x3+ax+b

Важной характеристикой эллиптической кривой является ее дискриминант, который для формы Вейерштрасса вычисляется так:Δ=4a3+27b2.

Дискриминант не должен быть равен нулю, иначе кривая уже не будет эллиптической, так как будут существовать точки перегиба, как на кривой y2=x3−3x+2 на рисунке справа.

Наверняка многим знакомо изображение эллиптической кривой, которое можно увидеть на рисунке слева. Здесь кривая вида y2=x3−3x+5 задана над полем рациональных чисел.

Однако, при использовании рациональных чисел возникает сложность с их округлением, и, как следствие, с неоднозначностью операций зашифрования и расшифрования. Поэтому в криптографии эллиптические кривые задаются над конечным полем, где координаты точек – это элементы поля. График кривой, конечно, потеряет свою былую привлекательность, плавные линии заменятся на точки, но мы же любим эллиптические кривые далеко не за это!

Нельзя не упомянуть еще одну характеристику эллиптических кривых, которая (СПОЙЛЕР!) еще одарит читателей своим присутствием в статье. Речь идет о j−инварианте, постоянной величине. Его вычисление для эллиптической кривой в форме Вейерштрасса тоже не обладает устрашающим воздействием на организм:j=17284a34a3+27b2

Свойства группы

Важным моментом в криптографии на эллиптических кривых является то, что точки эллиптической кривой с абстрактной бесконечно удаленной точкой образуют абелеву группу. Возьмем в качестве групповой операции сложение, тогда группа — это такая алгебраическая структура, которая обладает следующими свойствами:

• Замкнутость означает, что результат сложения элементов группы тоже является элементом группы. Переведем в термины эллиптической кривой: при сложении точек эллиптической кривой получается точка, принадлежащая этой же кривой.

  

  
  Как видно из рисунков сверху, геометрический смысл сложения точек на эллиптической кривой состоит в следующем: необходимо провести секущую через складываемые точки и отразить точку пересечения этой прямой с эллиптической кривой относительно оси Ox.
• Ассоциативность означает независимость результата сложения от изменения порядка действия.
• В группе должен существовать нейтральный элемент. Результат сложения любого элемента группы g и нейтрального будет равен тому же элементу.В эллиптических кривых роль нейтрального элемента играет бесконечно удаленная точка: P∞:P∞+P=P+P∞=P
  
• К каждому элементу должен существовать обратный к нему (относительно основной операции). При сложении элемента группы и обратного к нему получаем нейтральный элемент.
• Свойство коммутативности нам знакомо еще из школьной математики: от перестановки слагаемых сумма не меняется. Именно данное свойство и делает группу абелевой.

Пара слов о стойкости

Теперь поговорим немного о стойкости криптосистем, основанных на задаче дискретного логарифмирования. Пусть G – конечная циклическая группа, то есть, каждый ее элемент представим в виде степени одного-единственного элемента — образующей g: =G={1,g2,g3,...,gq−1}.

В зависимости от выбора группы G существуют различные методы решения задачи дискретного логарифмирования. Так, для решения задачи дискретного логарифмирования в конечном поле, на общее несчастье существуют не только универсальные алгоритмы (метод Полига-Хеллмана, ρ-метод Полларда и др.), которые имеют экспоненциальную сложность, но и специальные, имеющие субэкспоненциальную сложность (метод базы разложения, метод решета числового поля).

Если же в качестве образующей группы G взять точку эллиптической кривой, то криптожуликам придется довольствоваться лишь универсальными алгоритмами. Об этом говорит сайт https://intellect.icu . Поэтому криптография на эллиптических кривых «балует» пользователей меньшей длиной ключа.

Однако не все эллиптические кривые способны обеспечить высокий уровень стойкости в криптографических протоколах. Первую опасность представляют суперсингулярные кривые . Их преимущество состоит в легкости вычисления числа точек, в отличие от несуперсингулярных кривых. Есть немало факторов, по которым можно отличить суперсингулярную кривую от несуперсингулярной, однако в данной статье не будем заострять на этом внимание.

Данные кривые уязвимы к MOV атаке, которая позволяет сводить вычисление задачи дискретного логарифмирования в группе точек эллиптической кривой над полем Fq к задаче дискретного логарифмирования в конечном поле Fqk. Учитывая, что длина ключа в криптографии на эллиптических кривых меньше, и что для суперсингулярных кривых значение k не является большим, реализация данной атаки проходит крайне успешно для злоумышленника.

Ну так в чем же проблема? Используем подходящие эллиптические кривые и радуемся жизни! Но не тут-то было…

4 Алгоритмы постквантовой криптографии

Постквантовые криптографические конструкции способны спасти криптографический мир от квантовых атак. Хотя квантовый компьютер и уничтожит большинство традиционных алгоритмов (RSA, DSA, ECDSA), но сверхбыстрыми вычислениями не получится полностью избавиться от криптографии, так как постквантовая криптография, в основном, сосредоточена на пяти различных подходах, решающих проблему квантовых атак.

Криптография, основанная на хеш-функциях

Классическим примером является подпись Меркла с открытым ключом на основе хеш-дерева, Ральф Чарльз Меркл предложил этот алгоритм цифровой подписи в 1979 году, как интересную альтернативу цифровым подписям RSA и DSA. Основной недостаток схемы Меркла состоит в том, что для любого открытого ключа на основе хеш-функции существует ограничение на количество подписей, которые могут быть получены из соответствующего набора закрытых ключей. Этот факт и снижал уровень интереса к подписям такого типа, пока не появилась потребность в криптографии, устойчивой к воздействию квантовых компьютеров.

Криптография, основанная на кодах исправления ошибок

Является одним из наиболее перспективных кандидатов на пост-квантовые криптосистемы. Классическим примером является схемы шифрования McEliece и Niederreiter.

Криптография, основанная на решетках

Классическим примером схем шифрования являются Ring-Learning with Errors или более старые NTRU и GGH .

Криптография, основанная на многомерных квадратичных системах

Одной из самых интересных схем является подпись с открытым ключом Жака Патарина HFE, предложенная им в 1996 году, как обобщение предложений Matsumoto и Imai.

Шифрование с секретным ключом

Ярким примером является шифр Rijndael, предложенный в 1998 году, впоследствии переименованный в AES (Advanced Encryption Standard).

Шифрование с использованием суперсингулярной изогении

Это аналог протокола Диффи-Хеллмана, основанный на блуждании в суперсингулярном изогенном графе, позволяющий двум и более сторонам получить общий секретный ключ, используя незащищенный от прослушивания канал связи.

5 Примеры криптографических атак на RSA

В 1978 году документ, опубликованный разработчиками криптографического алгоритма с открытым ключом RSA (аббревиатура от фамилий Rivest, Shamir и Adleman), упоминал новый алгоритм Ричарда Шреппеля «linear sieve», который факторизовал любой RSA модуль } длины бит, используя простых операций. Таким образом, для того чтобы этот алгоритм требовал по меньшей мере простых операций, необходимо выбирать по крайней мере не меньше чем бит. Так как означает, что что-то сходится к {\displaystyle 0,5} при , то для выяснения правильного размера {\displaystyle n} при конечном {\displaystyle b} требуется более тщательный анализ скорости «linear sieve».

В 1988 году Джон Поллард ] предложил новый алгоритм факторизации, который называется Общий метод решета числового поля. Этот алгоритм факторизовал RSA-модуль размерности бит, используя простых операций. Таким образом, требуется выбирать не меньше чем бит, чтобы алгоритму потребовалось как минимум простых операций.

С 2008 года самые быстрые алгоритмы факторизации для классических компьютерных архитектур используют по меньшей мере простых операций. Были некоторые улучшения в значениях и в деталях , но не трудно догадаться, что {\displaystyle 1/3} оптимально, и что выбор модуля длиной примерно равной бит, позволит сопротивляться всем возможным атакам на классических компьютерах.

В 1994 году Питер Шор предложил алгоритм, который факторизовал любой RSA-модуль размерности (точнее ) кубитовых операций на квантовом компьютере размера порядка кубит (и небольшого количества вспомогательных вычислений на классическом компьютере). Пользуясь алгоритмом Шора, необходимо по крайней мере выбирать модуль {\displaystyle n} битовым размером не меньше чем бит, что является слишком большим числом для любого интересующего нас {\displaystyle b} .

6 Практические применения криптографических конструкций

Примеров алгоритмов, устойчивых к квантовым атакам, крайне мало. Но несмотря на больший уровень криптографической устойчивости, постквантовые алгоритмы неспособны вытеснить современные криптосистемы (RSA, DSA, ECDSA и др.).

Рассмотрим нападения на криптосистему с открытым ключом, а именно на алгоритм шифрования McEliece, который использует двоичные коды Гоппы[en]. Первоначально Роберт Мак-Элис ] представил документы, в которых коды длиной {\displaystyle n} взламываются за простых операций. Таким образом, требуется выбирать не меньше чем бит, чтобы алгоритму потребовалось как минимум простых операций. Несколько последующих работ сократили количество операций атаки до , но значительно меньше , если {\displaystyle n} большое. Поэтому улучшенные атаки до сих пор используют простых операций. Что касается квантовых компьютеров, то их использование приведет лишь к уменьшению константы {\displaystyle 0,5}, что совсем незначительно сократит количество операций, необходимых для взлома этого алгоритма.

Если система шифрования McEliece так хорошо защищена, то почему она не приходит на смену RSA? Все дело в эффективности — в частности, в размере ключа. Открытый ключ McEliece использует примерно ≈ бит, в то время как открытому ключу RSA достаточно около бит. Если бит для McEliece, будет меньше бит для RSA, но реальные уровни безопасности, такие как , позволяют RSA иметь открытый ключ в несколько тысяч бит, в то время как для McEliece размер ключа приближается к миллиону бит.

7 Квантовая угроза

В последнее время широкую популярность получают квантовые вычисления. Если в классическом компьютере наименьшая единица информации представляется битом, который может принимать значение либо 0, либо 1 в одно время, то в квантовом эту роль выполняют кубиты. Их особенность состоит в том, что кубит может находиться и в состоянии 0, и в состоянии 1 одновременно. Это и дает квантовым компьютерам их превосходящую вычислительную мощь. Например, если мы рассматриваем четыре бита информации, то из всевозможных 16 состояний мы можем выбрать лишь одно в один момент времени. 4 кубита же могут находиться в 16 состояниях одновременно, то есть в суперпозиции, и данная зависимость растет экспоненциально с каждым новым кубитом.

Если в классическом компьютере логические элементы получают на вход биты информации, а на выходе выдают однозначно определенный результат, то в квантовом компьютере в качестве логического элемента берется так называемый квантовый гейт (quantim gate), который манипулирует значением целой суперпозиции.

Важное явление, свойственное кубитам, – это запутанность. Например, имеем два запутанных кубита. Измерение состояния одного из них поможет узнать информацию о состоянии его пары без необходимости какой-либо проверки.

Следует отметить, что квантовый компьютер — это не замена привычным нам классическим, так как они быстрее лишь в выполнении вычислительных операций, где необходимо использовать всевозможные суперпозиции. Так что для просмотра видео с котиками использовать такую машину совсем нецелесообразно.

С одной стороны, появление квантового компьютера — это круто. Серьезно. Во многих сферах науки такая машина принесет немало пользы (например, при моделировании), однако для криптографии такой значимый прорыв будет критичен. А все потому, что в 1994 году Питер Шор предложил квантовый алгоритм, который позволяет разложить число не за стотыщмильонов лет, а за вполне обозримое время.

7.1 Об алгоритме Шора

Модификация данного алгоритма позволяет решить и задачу дискретного логарифмирования. Обобщенно метод Шора состоит в сведении сложновычислимой на классическом компьютере задачи к вычислению порядка некой функции. Если рассматривать разложение числа на множители, или задачу факторизации, то в качестве той самой функции берется f(x)=ax(modN), где N− число, которое раскладывается, а a−специально подобранное значение, взаимно простое с N.Далее по ходу алгоритма находится период функции w, который удовлетворяет соотношению:f(x+w)=f(x) и, как следствие, выполняется aw=1(modN). По найденном периоду вычислить собственный делитель числа N можно с помощью алгоритма Евклида: gcd(aw2,N).

Для того, чтобы решить задачу дискретного логарифмирования, то есть, найти такое k по данным y=gk, необходимо вычислить порядок другой функции, а именно: f(x1,x2)=gx1yx2, где g− образующая группы c числом элементов, равным q. Период функции представляется парой чисел (w1,w2): f(w1+x1,w2+x2)=f(x1,x2). Тогда решение задачи дискретного логарифмирования будет иметь вид: k=−w1w2(modq).

Таким образом, в методе Шора можно выделить квантовую и классическую часть, причем задача квантовой части алгоритма состоит в отыскании периода функции с использованием метода суперпозиции.

Неудивительно, что существование подобных алгоритмов и тенденция к разработке квантовых компьютеров подтолкнули специальные организации к размышлениям. Агентством национальной безопасности США, например, еще в 2015 году был анонсирован план перехода к алгоритмам, устойчивым к атаке на квантовом компьютере. А в 2016 году NIST США официально объявил о о запуске конкурса заявок на разработку алгоритмов постквантовой криптографии.

Постквантовая криптография не ограничивается одним примитивом, на самом деле, на данный момент рассматриваются несколько кандидатов. В их число могут, например, входить быстрые криптографические протоколы на решетках, схемы на хэш-функциях (например, подпись Меркла) и криптосистемы, основанные на некоммутативной алгебре (например, на группе кос). Свой выбор мы остановили на альтернативе, тесно связанной с эллиптическими кривыми (ведь мы их так любим!), а именно, с изогениями.

7.2 изогения – рациональное отображение и его использование в криптографии

Начнем с понятия: изогения – это рациональное отображение, переводящее точки одной эллиптической кривой в точки изогенной кривой, оставляя неподвижной бесконечно удаленную точку. Пусть имеем две изогенные эллиптические кривые E1 и E2. Изогенными они называются, если они заданы над одним полем и имеют одинаковое число точек.


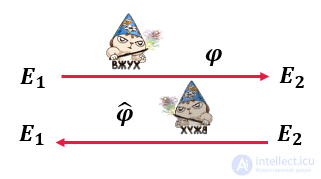
Так вот, изогения — это, по сути, небольшой ВЖУХ, который берет точку кривой E1 на вход, а на выходе выдает точку кривой E2. Ядром изогении называется множество точек на кривой E1, которые переходят в бесконечно удаленную точку кривой E2.

Для каждой изогении существует единственная дуальная изогения, выполняющая обратное преобразование. То есть, если изогения имеет следующий вид: 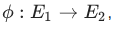, то дуальная к ней: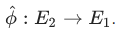

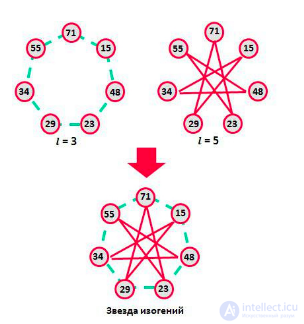
Если перемножить изогению и дуальную к ней, получим точку кривой E2, умноженную на целое число l, которую называют степенью изогении. Изогении простых степеней могут задавать перестановки на множестве j−инвариантов изогенных кривых. А последовательное наложение графов изогенных эллиптических кривых позволяет получить просто космически красивую звезду изогенных кривых, как на рисунке ниже.

Возможность применения изогений для построения криптосистем была предложена сравнительно недавно. В 2003 году автором E. Teske была опубликована работа, где изогении использовались в схеме с возможностью депонирования ключей. В 2006 году А. Г. Ростовцевым и А. Столбуновым схема шифрования Эль-Гамаля была адаптирована под изогении эллиптических кривых. В том же 2006 году для построения хэш-функций было предложено использовать графы изогенных суперсингулярных кривых. Важным и, можно сказать, переломным моментом в исследовании изогений является работа, опубликованная в 2010 году, где предлагается квантовый алгоритм, решающий задачу нахождения изогений несуперсингулярных кривых за субэкспоненциальное время. С этого момента исследования стали больше ориентированы на суперсингулярные кривые. Так, в сети уже можно найти схемы шифрования с открытым ключом, доказательства с нулевым разглашением, схему неоспоримой подписи и подписи вслепую.

7.3. Microsoft SIDH

Компания Microsoft тоже не осталась в стороне и в 2016 году выпустила библиотеку SIDH(Supersingular Isogeny Key Exchange) с открытым исходным кодом. Одним из преимуществ данной библиотеки является возможность использования эллиптических кривых в форме Монтгомери, которые защищают от атак по времени.

SIDH реализована на языке C и поддерживает использование Microsoft Visual Studio на OC Windows и LNU GCC и clang на OC Linux. В библиотеке представлена реализация базовых арифметических функций с возможностью поддержки различных платформ, включая x64, x86 и ARM. Большим плюсом к производительности является оптимизированная реализация операций на эллиптических кривых.
В библиотеке реализован протокол разделения ключа Диффи-Хеллмана на изогениях суперсингулярных кривых.

Эта схема была предложена авторами Jao и DeFeo. Упрощенно ее можно описать следующим образом. В качестве параметров криптосистемы используется общеизвестная суперсингулярная кривая E0 и зафиксированные на ней точки PA,QA,PB,QB. Для удобства за ходом протокола можно следить на рисунке ниже.

Пусть Алиса хочет разделить с Бобом не жизнь, а закрытый ключ. Для этого она генерирует случайные числа mA,nA и строит изогению ϕA:E0→EA, где ядро задается как .
Боб выполняет те же действия, но только строит уже изогению , где в качестве ядра выбирается .

Изогении ϕA и ϕB являются секретными и кому попало не передаются. Однако, и Боб, и Алиса могут без каких-либо последствий разделить точки на своих изогенных кривых, к тому же, переданы могут быть и сами кривые. Так и происходит на самом деле. Данный этап обозначен на рисунке пунктирной линией. Алиса передает Бобу точки ϕA(PB) и ϕA(QB), и саму кривую EA. Боб делает тоже самое: передает Алисе точки ϕB(PA) и ϕB(QA и кривую EB.

А это вообще законно?! Можешь быть спокоен, %username%, зная обе изогенные кривые, злоумышленник не сможет вычислить саму изогению.

Итак, Алиса и Боб обменялись данными, теперь подходим к завершающему и невероятно красивому этапу, а именно, к получению общего ключа. Зная образы точек PA и QA на кривой EB и случайные числа mB и nB, Боб сможет легко построить изогению ϕA′, а Алиса, обладающая тем же объемом информации, сможет построить изогению ϕB′. Изящное решение заключается в том, что изогении ϕA′ и ϕB′ приведут наших собеседников к кривой EAB, и в качестве ключа может быть взят ее j−инвариант.

Microsoft существенно упростила жизнь реализацией базовых функций, которые освобождают от кодинга вышеописанных шагов алгоритма. Перед тем, как реализовать схему разделения ключа, необходимо инициализировать структуру, в которой содержатся параметры криптосистемы:

CurveIsogeny = SIDH_curve_allocate(CurveIsogenyData);
    if (CurveIsogeny == NULL) {
        Status = CRYPTO_ERROR_NO_MEMORY;
        goto cleanup;
    }
    Status = SIDH_curve_initialize(CurveIsogeny, &random_bytes_test, CurveIsogenyData);
    if (Status != CRYPTO_SUCCESS) {
        goto cleanup;
    }

Сама структура:

typedef struct
{    
    CurveIsogeny_ID  CurveIsogeny;                             
    unsigned int     pwordbits;                               
    unsigned int     owordbits;                               
    unsigned int     pbits;                                   
    uint64_t         prime[MAXWORDS_FIELD];                   
    uint64_t         A[MAXWORDS_FIELD];                       
    uint64_t         C[MAXWORDS_FIELD];                       
    unsigned int     oAbits;                                   
    uint64_t         Aorder[MAXWORDS_ORDER];                  
    unsigned int     oBbits;                                  
    unsigned int     eB;                                      
    uint64_t         Border[MAXWORDS_ORDER];                   
    uint64_t         PA[2*MAXWORDS_FIELD];                    
    uint64_t         PB[2*MAXWORDS_FIELD];                    
    unsigned int     BigMont_A24;                             
    uint64_t         BigMont_order[BIGMONT_MAXWORDS_ORDER];   
    uint64_t         Montgomery_R2[MAXWORDS_FIELD];           
    uint64_t         Montgomery_pp[MAXWORDS_FIELD];           
    uint64_t         Montgomery_one[MAXWORDS_FIELD];          
} CurveIsogenyStaticData;

Чтобы Алисе и Бобу обменяться ключами, достаточно вызвать пару функций, которые не обязывают знать того, что же творится «под капотом». Генерация ключей происходит с помощью функций:

Status = KeyGeneration_A(PrivateKeyA,PublicKeyA, CurveIsogeny);

и

Status = KeyGeneration_B(PrivateKeyB,PublicKeyAB CurveIsogeny);

Алиса и Боб обмениваются вычисленными открытыми ключами и находят общий ключ:

Status = SecretAgreement_A(PrivateKeyA, PublicKeyB, SharedSecretA, false, CurveIsogeny); 

и

Status = SecretAgreement_B(PrivateKeyB, PublicKeyA, SharedSecretB, false, CurveIsogeny); 

Среди функций в библиотеке можно выделить и базовые арифметические, которые помогут в реализации своих протоколов. Это, например, j_inv, вычисляющая j-инвариант эллиптической кривой, inv_3_way, находящая значение мультипликативно обратного, удвоение точки и сложение точек – xDBLADD, утроение точки – xTPL и т.д. С полным описанием вы можете ознакомиться в публикации.

Выводы

Безусловно, пока сложно судить о необходимости постквантовой криптографии, когда мощного квантового компьютера, по сути, и нет… Однако суета в NSA и NIST не могут не наводить на подозрения. О реальных мотивах такой спешки нам остается только догадываться. В любом случае, никогда не помешает перестраховаться и начать изучение нового и интересного направления в криптографии, тем более, если это вполне осуществимо на практике.

Вау!! 😲 Ты еще не читал? Это зря!

• Криптография на решетках
• Алгоритм Шора

Анализ данных, представленных в статье про постквантовая криптография, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое постквантовая криптография, криптография и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Криптография и криптоанализ, Стеганография и Стегоанализ