2.6. Хэш-функции, хеш и хеширование, Криптографическая соль

Привет, Вы узнаете о том , что такое хеширование, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое хеширование, хэш-функции, криптографическая соль, кукушкино хеширование , настоятельно рекомендую прочитать все из категории Криптография и криптоанализ, Стеганография и Стегоанализ.

Для очень большого количества технологий безопасности (например, аутентификации, ЭЦП) применяются односторонние функции шифрования, называемые также хэш-функциями. Основное назначение подобных функций – получение из сообщения произвольного размера его дайджеста – значения фиксированного размера. Дайджест может быть использован в качестве контрольной суммы исходного сообщения, обеспечивая таким образом (при использовании соответствующего протокола) контроль целостности информации.

Хеш-функция (англ. hash function от hash — «превращать в фарш», «мешанина» ), или функция свертки — функция, осуществляющая преобразование массива входных данных произвольной длины в выходную битовую строку установленной длины, выполняемое определенным алгоритмом. Преобразование, производимое хеш-функцией, называется хеширование м. Исходные данные называются входным массивом, «ключом» или «сообщением». Результат преобразования называется «хешем», «хеш-кодом», «хеш-суммой», «сводкой сообщения». Хэш-функция - это функция, которая принимает на вход некоторые данные произвольной длины и преобразует их в фиксированную строку фиксированной длины, которая обычно называется хэш-значением или хэш-кодом. Целью хэш-функций является быстрое и эффективное отображение входных данных на хэш-значение таким образом, чтобы даже небольшие изменения во входных данных приводили к существенным изменениям в хэш-значении. Это делает хэш-функции полезными для многих целей, таких как проверка целостности данных, хранение паролей, поиск данных в хэш-таблицах и другие приложения.

Хеш - это своего рода это отражение в искаженном зеркале нейкой информации, по которому практически однозначно можно сравнивать первоисточники (не считая редких коллизий.)

Хеш-функции применяются в следующих случаях:

• при построении ассоциативных массивов;
• при поиске дубликатов в сериях наборов данных;
• при построении уникальных идентификаторов для наборов данных;
• при вычислении контрольных сумм от данных (сигнала) для последующего обнаружения в них ошибок (возникших случайно или внесенных намеренно), возникающих при хранении и/или передаче данных;
• при сохранении паролей в системах защиты в виде хеш-кода (для восстановления пароля по хеш-коду требуется функция, являющаяся обратной по отношению к использованной хеш-функции);
• при выработке электронной подписи (на практике часто подписывается не само сообщение, а его «хеш-образ»);
• и др.

В общем случае (согласно принципу Дирихле) нет однозначного соответствия между хеш-кодом и исходными данными. Возвращаемые хеш-функцией значения менее разнообразны, чем значения входного массива. Случай, при котором хеш-функция преобразует более чем один массив входных данных в одинаковые сводки, называется «коллизией». Вероятность возникновения коллизий используется для оценки качества хеш-функций.

Существует множество алгоритмов хеширования, отличающихся различными свойствами. Примеры свойств:

• разрядность;
• вычислительная сложность;
• криптостойкость.

Выбор той или иной хеш-функции определяется спецификой решаемой задачи. Простейшим примером хеш-функции может служить «обрамление» данных циклическим избыточным кодом (англ. CRC, cyclic redundancy code).

Перцептивное и криптографическое хеширование

Существует также так называемое Перцептивное хеширование — это использование алгоритма снятия отпечатков пальцев , который создает фрагмент, хеш или отпечаток пальца различных форм мультимедиа . Перцептивный хэш — это тип хеша, чувствительного к местонахождению , который аналогичен, если характеристики мультимедиа схожи. В этом отличие от криптографического хеширования , которое основано на лавинном эффекте небольшого изменения входного значения, вызывающего резкое изменение выходного значения. Перцептивные хэш-функции широко используются при обнаружении случаев нарушения авторских прав в Интернете , а также в цифровой криминалистике из-за возможности корреляции между хэшами, позволяющей находить похожие данные (например, с другим водяным знаком ).

Основные свойства хэш-функции:

• 1) на вход хэш-функции подается сообщение произвольной длины;
• 2) на выходе хэш-функции формируется блок данных фиксированной длины;
• 3) значения на выходе хэш-функции распределены по равномерному закону;
• 4) при изменении одного бита на входе хэш-функции существенно изменяется выход.

Кроме того, для обеспечения устойчивости хэш-функции к атакам она должна удовлетворять следующим требованиям:

1) если мы знаем значение хэш-функции h, то задача нахождения сообщения M такого, что Н(М)=h, должна быть вычислительно трудной;

2) при заданном сообщении M задача нахождения другого сообщения M^’, такого, что Н(М)=H(M^’), должна быть вычислительно трудной

Важные характеристики хэш-функций:

1. Детерминизм: Для одинаковых входных данных хэш-функция всегда должна генерировать один и тот же хэш-код.

2. Фиксированная длина вывода: Хэш-функция генерирует хэш-код фиксированной длины, независимо от длины входных данных.

3. Быстродействие: Хорошие хэш-функции должны работать быстро, чтобы эффективно обрабатывать большие объемы данных.

4. Равномерное распределение: Хэш-значения должны быть равномерно распределены, чтобы избежать коллизий (ситуаций, когда разным входным данным соответствует одинаковый хэш-код).

5. Сопротивляемость к коллизиям: Хорошие хэш-функции должны минимизировать вероятность коллизий, когда двум разным входам соответствует одинаковый хэш-код.

Если хэш-функция будет удовлетворять перечисленным свойствам, то формируемое ею значение будет уникально идентифицировать сообщения, и всякая попытка изменения сообщения при передаче будет обнаружена путем выполнения хэширования на принимающей стороне и сравнением с дайджестом, полученным на передающей стороне.

Еще одной особенностью хэш-функций является то, что они не допускают обратного преобразования – получить исходное сообщения по его дайджесту невозможно. Поэтому их называют еще односторонними функциями шифрования.

Хэш-функции строятся по итеративной схеме, когда исходное сообщение разбивается на блоки определенного размера, и над ними выполняются ряд преобразований с использованием как обратимых, так и необратимых операций. Как правило, в состав хэширующего преобразования включается сжимающая функция, поскольку его выход зачастую по размеру меньше блока, подаваемого на вход. На вход каждого цикла хэширования подается выход предыдущего цикла, а также очередной блок сообщения. Таким образом, на каждом цикле выход хэш-функции h_i представляет собой хэш первых i блоков.

Если вспомнить, насколько рандомизируют входное сообщение блочные шифры, можно в качестве функции хэш-преобразования использовать какой-нибудь блочный шифр. То, что блочные шифры являются обратимыми преобразованиями, не противоречит свойствам хэш-функции, поскольку блочный шифр необратим по ключу шифрования, и, если в качестве ключа шифрования использовать выход предыдущего шага хэш-преобразования, а в качестве шифруемого сообщения очередной блок сообщения (или наоборот), то можно получить хэш-функцию с хорошими криптографическими характеристиками. Такой подход использован, например, в российском стандарте хэширования – ГОСТ Р 34.11-94. Эта хэш-функция формирует 256-битное выходное значение, используя в качестве преобразующей операции блочный шифр ГОСТ 28147-89 (рис.2.17). Функция хэширования H получает на вход хэш, полученный на предыдущем шаге (значение h₀ произвольное начальное число), а также очередной блок сообщения m_i. Ее внутренняя структура представлена на рис.2.18. Здесь в блоке шифрующего преобразования для модификации h_i в s_i используется блочный шифр ГОСТ 28147-89. Перемешивающее преобразование представляет собой модифицированную перестановку Фейштеля. Для последнего блока m_N (N – общее количество блоков сообщения) выполняется набивка до размера 256 бит с добавлением истинной длины сообщения. Параллельно подсчитывается контрольная сумма сообщения S и суммарная длина L, которые участвуют в финальной функции сжатия.

Рис.2.17. Общая схема хэшироваения по ГОСТ Р 34.11 - 94

Рис.2.18. Структура функции хэширования в ГОСТ Р 34.11-94

Основным недостатком хэш-функций на основе блочных шифров является невысокая скорость их работы. Поэтому были спроектированы ряд специализированных алгоритмов, которые, обеспечивая аналогичную стойкость к атакам, выполняют гораздо меньшее количество операций над входными данными и обеспечивают большую скорость работы. Примерами подобного рода алгоритмов являются : MD2, MD4, MD5, RIPEMD –160, SHA. Рассмотрим подробнее структуру алгоритма хэширования SHA (Secure Hash Algorithm), который описан в стандарте SHS и обеспечивает безопасность электронной цифровой подписи DSA, формируя 160-битный дайджест сообщения.

Сначала сообщение разбивается на блоки длиной 512 бит. Если длина сообщения не кратна 512, к последнему блоку приписывается справа 1, после чего он дополняется нулями до 512 бит. В конец последнего блока записывается код длины сообщения. В результате сообщение приобретает вид n 512-разрядных блоков M₁,M₂,…,M_n.

Алгоритм SHA использует 80 логических функций f₀,f₁,…,f₇₉, которые производят операции над тремя 32-разрядными словами (B,C,D):

В алгоритме используются также специальным образом инициализированные 4 константы K_i и 5 начальных значений H_i.

Делим массив M на группы из 16 слов W₀, W₁,…,W₁₅ (W₀ самое левое слово).

Для t = 16 - 79 W_t = S¹(W_t-3 Å W_t-8 Å W_t-14 Å W_t-16)

S^k означает операцию циклического сдвига влево на k разрядов.

Пусть теперь A = H₀, B = H₁, C = H₂, D = H₃, E = H₄.
for t = 0 to 79 do
TEMP = S⁵(A) + f_t(B,C,D) + E + W_t + K_i.
E = D; D = C; C = S³⁰(B); B = A; A = TEMP;
Пусть H₀ = H₀ + A; H₁ = H₁ + B; H₂ = H₂ + C; H₃ = H₃ + D; H₄ = H₄ + E.

Графически один цикл SHA представлен на рис.2.19.

Рис.2.19. Один цикл преобразования SHA

В результате обработки массива М будет получено 5 слов H₀, H₁, H₂, H₃, H₄ с общей длиной 160 бит, которые и образуют дайджест сообщения.

Из приведенных данных ясно, что сложность американского стандарта хэширования ниже, чем у российского. Российский стандарт предполагает выполнение четырех шифрований за один цикл выработки хэша, или в общей сложности 128 раундов. Каждый раунд шифрования требует примерно полтора десятка элементарных машинных операций, что существенно увеличивает затраты машинного времени на выполнение линейных перемешивающих операций. Один раунд выработки хэша SHA гораздо проще: он весь может быть реализован примерно за 15-20 команд, общее количество раундов всего 80, и за один цикл выработки хэша обрабатывается вдвое больше исходных данных — 512 против 256 в ГОСТ P34.ll -94. Таким образом, можно предположить, что быстродействие программных реализаций SHA будет примерно в 3-6 раз быстрее, чем у отечественного стандарта.

Основная задача хэш-функций – генерация дайджестов, уникальных для конкретного документа. Если для двух различных входных блоков хэш-функция дает одинаковый дайджест, такая ситуация называетсяхэш-коллизией. Из теоремы, носящей название «парадокс дней рождения», следует, что для n-битного хэш-значения необходимо в среднем 2^n/2 различных входных сообщений, чтобы возникла коллизия. Это делает практически невозможным изменение документа при его подписи с помощью, например, алгоритма SHА путем простого подбора, поскольку при таком подходе потребуется сгенерировать около 2⁸⁰ различных сообщений, чтобы получить аналогичное подменяемому по получаемому дайджесту. Эта цифра недостижима для современного уровня технологий.

Виды «хеш-функций»

«Хорошая» хеш-функция должна удовлетворять двум свойствам:

• быстрое вычисление;
• минимальное количество «коллизий».

Введем обозначения:

• — количество «ключей» (входных данных);
• — хеш-функция, имеющая не более различных значений (выходных данных).

То есть:

.

В качестве примера «плохой» хеш-функции можно привести функцию с , которая десятизначному натуральному числу сопоставляет три цифры, выбранные из середины двадцатизначного квадрата числа . Казалось бы, значения «хеш-кодов» должны равномерно распределяться между «000» и «999», но для «реальных» данных это справедливо лишь в том случае, если «ключи» не имеют «большого» количества нулей слева или справа .

Рассмотрим несколько простых и надежных реализаций «хеш-функций».

«Хеш-функции», основанные на делении

1. «Хеш-код» как остаток от деления на число всех возможных «хешей»

Хеш-функция может вычислять «хеш» как остаток от деления входных данных на :

,

где — количество всех возможных «хешей» (выходных данных).

При этом очевидно, что при четном значение функции будет четным при четном и нечетным — при нечетном . Об этом говорит сайт https://intellect.icu . Также не следует использовать в качестве степень основания системы счисления компьютера, так как «хеш-код» будет зависеть только от нескольких цифр числа , расположенных справа, что приведет к большому количеству коллизий. На практике обычно выбирают простое ; в большинстве случаев этот выбор вполне удовлетворителен.

2. «Хеш-код» как набор коэффициентов получаемого полинома

Хеш-функция может выполнять деление входных данных на полином по модулю два. В данном методе должна являться степенью двойки, а бинарные ключи () представляются в виде полиномов, в качестве «хеш-кода» «берутся» значения коэффициентов полинома, полученного как остаток от деления входных данных на заранее выбранный полином степени :

При правильном выборе гарантируется отсутствие коллизий между почти одинаковыми ключами .

«Хеш-функции», основанные на умножении

Обозначим символом количество чисел, представимых машинным словом. Например, для 32-разрядных компьютеров, совместимых с IBM PC, .

Выберем некую константу так, чтобы была взаимно простой с . Тогда хеш-функция, использующая умножение, может иметь следующий вид:

В этом случае на компьютере с двоичной системой счисления является степенью двойки, и будет состоять из старших битов правой половины произведения .

Одним из преимуществ хеш-функций, основанных на делении и умножении, является выгодное использование неслучайности реальных ключей. Например, если ключи представляют собой арифметическую прогрессию (например, последовательность имен «Имя 1», «Имя 2», «Имя 3»), хеш-функция, использующая умножение, отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшит количество коллизий по сравнению со случайной ситуацией .

Одной из хеш-функций, использующих умножение, является хеш-функция, использующая хеширование Фибоначчи. Хеширование Фибоначчи основано на свойствах золотого сечения. В качестве константы здесь выбирается целое число, ближайшее к и взаимно простое с , где — это золотое сечение .

Хеширование строк переменной длины

Вышеизложенные методы применимы и в том случае, если необходимо рассматривать ключи, состоящие из нескольких слов, или ключи переменной длины.

Например, можно скомбинировать слова в одно при помощи сложения по модулю или операции «исключающее или». Одним из алгоритмов, работающих по такому принципу, является хеш-функция Пирсона.

Хеширование Пирсона — алгоритм, предложенный Питером Пирсоном (англ. Peter Pearson) для процессоров с 8-битовыми регистрами, задачей которого является быстрое преобразование строки произвольной длины в хеш-код. На вход функция получает слово , состоящее из символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. При этом значение хеш-кода зависит от каждого символа входного слова.

Алгоритм можно описать следующим псевдокодом, который получает на вход строку и использует таблицу перестановок :

h := 0
for each c in W loop
  index := h xor c
  h := T[index]
end loop
return h

Среди преимуществ алгоритма:

• простоту вычисления;
• отсутствие таких входных данных, для которых вероятность коллизии наибольшая;
• возможность модификации в идеальную хеш-функцию .

В качестве альтернативного способа хеширования ключей , состоящих из символов (), можно предложить вычисление

Идеальное хеширование

Идеальной хеш-функцией (англ. perfect hash function) называется такая функция, которая отображает каждый ключ из набора во множество целых чисел без коллизий. В математике такое преобразование называется инъективным отображением.

Описание

1. Функция называется идеальной хеш-функцией для , если она инъективна на .
2. Функция называется минимальной идеальной хеш-функцией для , если она является идеальной хеш-функцией и .
3. Для целого функция называется -идеальной хеш-функцией (k-PHF) для , если для каждого имеем .

Идеальное хеширование применяется, если требуется присвоить уникальный идентификатор ключу без сохранения какой-либо информации о ключе. Пример использования идеального (или скорее -идеального) хеширования: размещение хешей, связанных с данными, хранящимися в большой и медленной памяти, в небольшой и быстрой памяти. Размер блока можно выбрать таким, чтобы необходимые данные считывались из медленной памяти за один запрос. Подобный подход используется, например, в аппаратных маршрутизаторах. Также идеальное хеширование используется для ускорения работы алгоритмов на графах, если представление графа не умещается в основной памяти .

Универсальное хеширование

Универсальным хешированием называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор хеш-функции из заданного семейства по случайному алгоритму. Универсальное хеширование обычно отличается низким числом коллизий, применяется, например, при реализации хеш-таблиц и в криптографии.

Описание

Предположим, что требуется отобразить ключи из пространства в числа . На входе алгоритм получает данные из некоторого набора размерностью . Набор заранее неизвестен. Как правило, алгоритм должен обеспечить наименьшее число коллизий, чего трудно добиться, используя какую-то определенную хеш-функцию. Число коллизий можно уменьшить, если каждый раз при хешировании выбирать хеш-функцию случайным образом. Хеш-функция выбирается из определенного набора хеш-функций, называемого универсальным семейством .

Методы борьбы с коллизиями

Коллизией (иногда конфликтом или столкновением) называется случай, при котором одна хеш-функция для разных входных блоков возвращает одинаковые хеш-коды.

Методы борьбы с коллизиями в хеш-таблицах

Большинство первых работ, описывающих хеширование, посвящено методам борьбы с коллизиями в хеш-таблицах. Тогда хеш-функции применялись при поиске текста в файлах большого размера. Существует два основных метода борьбы с коллизиями в хеш-таблицах:

1. метод цепочек (метод прямого связывания);
2. метод открытой адресации.

При использовании метода цепочек в хеш-таблице хранятся пары «связный список ключей» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; если хеш-код был получен ранее (для другого ключа), ключ добавляется в существующий список ключей, парный хеш-коду; иначе создается новая пара «список ключей» — «хеш-код», и ключ добавляется в созданный список. В общем случае, если имеется ключей и списков, средний размер хеш-таблицы составит . В этом случае при поиске по таблице по сравнению со случаем, в котором поиск выполняется последовательно, средний объем работ уменьшится примерно в раз.

При использовании метода открытой адресации в хеш-таблице хранятся пары «ключ» — «хеш-код». Для каждого ключа хеш-функцией вычисляется хеш-код; пара «ключ» — «хеш-код» сохраняется в таблице. В этом случае при поиске по таблице по сравнению со случаем, в котором используются связные списки, ссылки не используются, выполняется последовательный перебор пар «ключ» — «хеш-код», перебор прекращается после обнаружения нужного ключа. Последовательность, в которой просматриваются ячейки таблицы, называется последовательностью проб .

Применение хэш-функций:

1. Хэширование паролей: Вместо хранения самих паролей, системы могут хранить хэш-коды паролей. Это обеспечивает безопасность в случае утечки данных.

2. Цифровые подписи: Хэш-функции используются для создания цифровых подписей, обеспечивая целостность и аутентичность данных.

3. Хэш-таблицы: Хэш-функции используются для реализации хэш-таблиц, позволяющих эффективно хранить и быстро находить данные.

4. Контроль целостности данных: Хэш-функции могут использоваться для проверки целостности файлов и данных, например, при скачивании файлов из интернета.

5. Криптография: В криптографии хэш-функции используются для создания цифровых подписей, хеширования сообщений и других операций, обеспечивающих безопасность данных и информации.

Примерами хэш-функций являются MD5, SHA-1, SHA-256, bcrypt и другие. Однако стоит отметить, что с течением времени некоторые из них могли стать уязвимыми или устаревшими, и рекомендуется использовать более современные и безопасные алгоритмы хэширования.

криптографическая соль Соль (криптография)

Для защиты паролей и цифровых подписей от подделки создано несколько методов, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление к входным данным так называемой криптографической «соли» — строки случайных данных; иногда «соль» добавляется и к хеш-коду. Добавление случайных данных значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется при сохранении паролей в UNIX-подобных операционных системах.

Применение хеш-функций

Хеш-функции широко используются в криптографии.

Хеш используется как ключ во многих структурах данных — хеш-таблицаx, фильтрах Блума и декартовых деревьях.

Криптографические хеш-функции

Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того, чтобы хеш-функция считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:

• необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных , для которого ;
• стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого ;
• стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений , имеющих одинаковый хеш.

Данные требования не являются независимыми:

• обратимая функция нестойка к коллизиям первого и второго рода;
• функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.

Не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.

Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно вычислений хеш-функции. Поэтому n-битовая хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для нее близка к .

Криптографические хеш-функции должны иметь лавинный эффект — при малейшем изменении аргумента значение функции сильно изменяется. В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа .

Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев вместо паролей хранятся значения их хеш-кодов.

Контрольные суммы

Алгоритмы вычисления контрольных сумм — несложные, быстрые и легко реализуемые аппаратно алгоритмы, используемые для защиты данных от непреднамеренных искажений, в том числе — от ошибок аппаратуры. С точки зрения математики такие алгоритмы являются хеш-функциями, вычисляющими контрольный код. Контрольный код применяется для обнаружения ошибок, которые могут возникнуть при передаче и хранении информации.

Алгоритмы вычисления контрольных сумм по скорости вычисления в десятки и сотни раз быстрее, чем криптографические хеш-функции, и значительно проще в аппаратном исполнении.

Платой за столь высокую скорость является отсутствие криптостойкости — возможность легко «подогнать» сообщение под заранее известную контрольную сумму. Также обычно разрядность контрольных сумм (типичное число: 32 бита) ниже, чем разрядность криптографических хешей (типичные числа: 128, 160 и 256 бит), что означает возможность возникновения непреднамеренных коллизий.

Простейшим алгоритмом вычисления контрольной суммы является деление сообщения (входных данных) на 32- или 16-битовые слова с последующим суммированием слов. Такой алгоритм применяется, например, в протоколах TCP/IP.

Как правило, алгоритмы вычисления контрольных сумм должны обнаруживать типичные аппаратные ошибки, например, должны обнаруживать несколько подряд идущих ошибочных бит до заданной длины. Семейство алгоритмов так называемых «циклических избыточных кодов» удовлетворяет этим требованиям. К ним относится, например, алгоритм CRC32, применяемый в устройствах Ethernet и в формате сжатия данных ZIP.

Контрольная сумма, например, может быть передана по каналу связи вместе с основным текстом (данными). На приемном конце, контрольная сумма может быть рассчитана заново и может сравниваться с переданным значением. Если будет обнаружено расхождение, то при передаче возникли искажения, и можно запросить повторную передачу.

Пример применения хеширования в быту — подсчет количества чемоданов, перевозимых в багаже. Для проверки сохранности чемоданов не требуется проверять сохранность каждого чемодана, достаточно посчитать количество чемоданов при погрузке и выгрузке. Совпадение чисел будет означать, что ни один чемодан не потерян. То есть, число чемоданов является хеш-кодом.

Данный метод можно дополнить для защиты передаваемой информации от фальсификации (метод MAC). В этом случае хеширование производится криптостойкой функцией над сообщением, объединенным с секретным ключом, известным только отправителю и получателю сообщения. Криптоаналитик, перехватив сообщение и значение хеш-функции, не сможет восстановить код, то есть не сможет подделать сообщение (см. имитозащита).

Геометрическое хеширование

Геометрическое хеширование (англ. geometric hashing) — метод, широко применяемый в компьютерной графике и вычислительной геометрии для решения задач на плоскости или в трехмерном пространстве, например для нахождения ближайших пар точек среди множества точек или для поиска одинаковых изображений. Хеш-функция в данном методе обычно получает на вход какое-либо метрическое пространство и разделяет его, создавая сетку из клеток. Хеш-таблица в данном случае является массивом с двумя или более индексами и называется «файлом сетки» (англ. grid file). Геометрическое хеширование применяется в телекоммуникациях при работе с многомерными сигналами .

Ускорение поиска данных Хеш-таблица

Хеш-таблицей называется структура данных, позволяющая хранить пары вида «ключ» — «хеш-код» и поддерживающая операции поиска, вставки и удаления элемента. Хеш-таблицы применяются с целью ускорения поиска, например, при записи текстовых полей в базе данных может рассчитываться их хеш-код, и данные могут помещаться в раздел, соответствующий этому хеш-коду. Тогда при поиске данных надо будет сначала вычислить хеш-код текста, и сразу станет известно, в каком разделе их надо искать. То есть искать надо будет не по всей базе, а только по одному ее разделу, а это ускоряет поиск.

Бытовым аналогом хеширования в данном случае может служить размещение слов в словаре в алфавитном порядке. Первая буква слова является его хеш-кодом, и при поиске просматривается не весь словарь, а только слова, начинающиеся на нужную букву.

кукушкино хеширование

Пример кукушкиного хеширования. Стрелки показывают альтернативное положение ключа. Новое значение, которое вставляется в ячейку A, выталкивая A в альтернативную ячейку, занимаемую ключом B, значение B переносится в альтернативное место, которое в настоящее время не занято. Вставка нового значения в ячейку H завершается неудачей — H входит в цикл (вместе с W), так что только что вставленный элемент должен быть вытолкнут.

Кукушкино хеширование — это схема в программировании для решения коллизий значений хеш-функций в таблице с постоянным временем выборки в худшем случае^[en]. Имя происходит от поведения некоторых видов кукушек, когда птенец кукушки выталкивает яйца или других птенцов из гнезда сразу после того, как вылупится. Аналогичное происходит в кукушкином хеше, когда вставка нового ключа в таблицу может вытолкнуть старый ключ в другое место в таблице.

Кукушкино хеширование было впервые описано Расмусом Пажом и Флеммингом Фришем Родлером в 2001 .

Операции

Кукушкино хеширование является видом открытой адресации , в которой каждая непустая ячейка хеш-таблицы содержит ключ или пару ключ–значение . Хеш-функция используется для определения места для каждого ключа, и его присутствие в таблице (или значение, ассоциированное с ним) может быть найдено путем проверки этой ячейки в таблице. Однако открытая адресация страдает от коллизий, которые случаются, когда более одного ключа попадают в одну ячейку. Основная идея кукушкиного хеширования заключается в разрешении коллизий путем использования двух хеш-функций вместо одной. Это обеспечивает два возможных положения в хеш-таблице для каждого ключа. В одном из обычных вариантов алгоритма хеш-таблица разбивается на две меньшие таблицы меньшего размера и каждая хеш-функция дает индекс в одну из этих двух таблиц. Можно обеспечить также для обеих хеш-функций индексирование внутри одной таблицы.

Выборка требует просмотра всего двух мест в хеш-таблице, что требует постоянного времени в худшем случае (см. «O» большое и «o» малое). Это контрастирует с многими другими алгоритмами хеш-таблиц, которые не обеспечивают постоянное время выборки в худшем случае. Удаление также может быть осуществлено очищением ячейки, содержащей ключ за постоянное время в худшем случае, что осуществляется проще, чем в других схемах, таких как линейное зондирование.

Когда вставляется новый ключ и одна из двух ячеек пуста, ключ может быть помещен в эту ячейку. В случае же, когда обе ячейки заняты, необходимо переместить другие ключи в другие места (или, наоборот, на их прежние места), чтобы освободить место для нового ключа. Используется жадный алгоритм — ключ помещается в одну из возможных позиций, «выталкивая» любой ключ, который был в этой позиции. Вытолкнутый ключ затем помещается в его альтернативную позицию, снова выталкивая любой ключ, который мог там оказаться. Процесс продолжается, пока не найдется пустая позиция. Возможен, однако, случай, когда процесс вставки заканчивается неудачей, попадая в бесконечный цикл или когда образуется слишком длинная цепочка (длиннее, чем заранее заданный порог, зависящий логарифмически от длины таблицы). В этом случае хеш-таблица перестраивается на месте^[en] с новыми хеш-функциями:

Нет необходимости размещения новой таблицы для повторного хеширования — мы можем просто просматривать таблицу для удаления и повторной вставки всех ключей, которые находятся не в той позиции, в которой должны были бы стоять. Pagh & Rodler, «Cuckoo Hashing»

Теория

Ожидаемое время вставки постоянно , даже если принимать во внимание возможную необходимость перестройки таблицы, пока число ключей меньше половины емкости хеш-таблицы, т.е. коэффициент загрузки меньше 50 %.

Чтобы обеспечить это, используется теория случайных графов — можно образовать неориентированный граф, называемый «кукушкиным графом», в котором вершинами являются ячейки хеш-таблицы, а ребра для каждого хешируемого соединяют два возможных положения (ячейки хеш-таблицы). Тогда жадный алгоритм вставки множества значений в кукушкину хеш-таблицу успешно завершается тогда и только тогда, когда кукушкин граф для этого множества значений является псевдолесом, графом максимум с одним циклом в каждой компоненте связности. Любой порожденный вершинами подграф с числом ребер, большим числа вершин, соответствует множеству ключей, для которых число слотов в хеш-таблице недостаточно. Если хеш-функция выбирается случайно, кукушкин граф будет случайным графом в модели Эрдеша – Реньи^[en]. С высокой степенью вероятности для случайного графа, в котором отношение числа ребер к числу вершин ограничено сверху 1/2, граф является псевдолесом и алгоритм кукушкиного хеширования располагает успешно все ключи. Более того, та же теория доказывает, что ожидаемый размер компонент связности кукушкиного графа мал, что обеспечивает постоянное ожидаемое время вставки .

Пример

Пусть даны следующие две хеш-функции:

Столбцы в следующих двух таблицах показывают состояние хеш-таблицы после вставки элементов.

Циклы

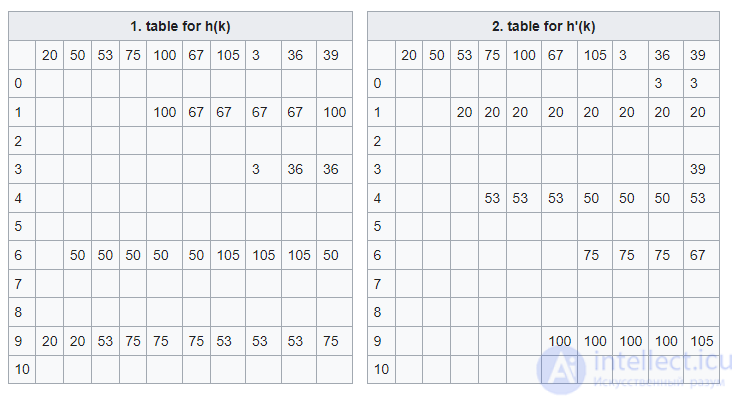
Если вы хотите вставить элемент 6, вы получите бесконечный цикл. В последней строке таблицы мы находим ту же начальную ситуацию, что и в начале.

Вариации

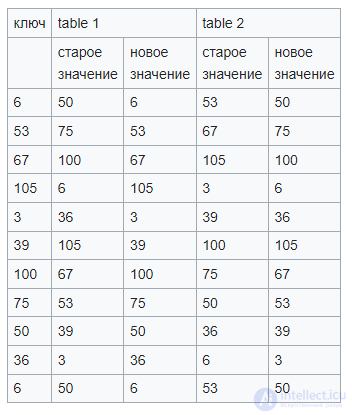
Изучались некоторые вариации кукушкиного хеширования, в основном с целью улучшить использование пространства путем увеличения коэффициента загрузки^[en]. В этих вариантах может достигаться порог загрузки больше 50 %. Некоторые из этих методов могут быть использованы для существенного уменьшения числа необходимых перестроек структуры данных.

От обобщения кукушкиного хеширования, использующего более двух хеш-функций, можно ожидать лучшего использования хеш-таблицы, жертвуя некоторой скоростью выборки и вставки. Использование трех хеш-функций повышает коэффициент загрузки до 91 % . Другое обобщение кукушкиного хеширования, называемое блочным кукушкиным хешированием, содержит более одного ключа на ячейку. Использование двух ключей на ячейку позволяет повысить загрузку выше 80 % .

Еще один изучавшийся вариант — кукушкино хеширование с запасом. «Запас» — это массив ключей постоянной длины, который используется для хранения ключей, которые не могут быть успешно вставлены в главную хеш-таблицу. Эта модификация уменьшает число неудач до обратно-полиномиальной функции со степенью, которая может быть произвольно большой, путем увеличения размера запаса. Однако большой запас означает более медленный поиск ключа, которого нет в основной таблице, либо если он находится в запасе. Запас можно использовать в комбинации с более чем двумя хеш-функциями или с блоковым кукушкиным хешированием для получения как высокой степени загрузки, так и малого числа неудач вставки . Анализ кукушкиного хеширования с запасом распространился и на практические хеш-функции, не только случайные модели хеш-функций, используемые в теоретическом анализе хеширования .

Некоторые исследователи предлагают использовать в некоторых кэшах процессора упрощенное обобщение кукушкиного хеширования, называемого несимметричным ассоциативным кэшем.

Сравнение с аналогичными структурами

Есть другие алгоритмы, которые используют несколько хеш-функций, в частности фильтр Блума, эффективная по памяти структура данных для нечетких множеств. Альтернативная структура данных для задач с теми же нечеткими множествами, основанная на кукушкином хешировании, называемая кукушкиным фильтром, использует даже меньшую память и (в отличие от классических фильтров Блума) позволяет удаление элемента, не только вставку и проверку существования. Однако теоретический анализ этих методов проведен существенно слабее, чем анализ фильтров Блума .

Исследования, проведенные Жуковским, Хеманом и Бонзом , показали, что кукушкино хеширование существенно быстрее метода цепочек для малых хеш-таблиц, находящихся в кэше современных процессоров. Кеннет Росс^[10] показал блочную версию кукушкиного хеширования (блок содержит более одного ключа), который работает быстрее обычных методов для больших хеш-таблиц в случае высокого коэффициента загрузки. Скорость работы блочной версии кукушкиной хеш-таблицы позднее исследовал Аскитис^[11] по сравнению с другими схемами кэширования.

Обзор Мутцемахера представляет открытые проблемы, связанные с кукушкиным хешированием.

Вау!! 😲 Ты еще не читал? Это зря!

• Хеш-таблица
• Криптографическая хеш-функция
• Хеш-функция облегченной криптографии
• хеширование в программировании на языке си , хеширование в программировании ,
• скользящий хеш , rolling hash , прокручивающий хеш , кольцевой хеш ,
• Перцептивное хеширование
• Совершенная функция хеширования
• Линейное зондирование
• Двойное хеширование
• Коллизия хеш-функции
• Хеширование
• Квадратичное зондирование
• Хеширование «Классики»
• [[b12468]]
• геометрическое хеширование ,

В заключение, эта статья об хеширование подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое хеширование, хэш-функции, криптографическая соль, кукушкино хеширование и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Криптография и криптоанализ, Стеганография и Стегоанализ