Лекция
Сразу хочу сказать, что здесь никакой воды про показатели надежности неремонтируемых объектов, и только нужная информация. Для того чтобы лучше понимать что такое показатели надежности неремонтируемых объектов , настоятельно рекомендую прочитать все из категории Теория надёжности.
Такие объекты работают до первого отказа. Для оценки надежности таких объектов используют вероятностные характеристики случайной величины – наработки до отказа Т. Под наработкой понимают продолжительность или объем работы объекта, измеряемые в часах, километрах, циклах и т.д.
Полной характеристикой любой случайной величины является ее закон распределения, т.е. соотношение между возможными значениями случайной величины и соответствующими этим значениям вероятностями.
К числу показателей надежности относятся:
функция надежности p(t);
плотность распределения наработки до отказа f(t);
интенсивность отказов l(t).
Функцией надежности называют функцию, выражающую вероятность того, что Т – случайная наработка до отказа объектов – будет больше заданной наработки (0,t), отсчитываемой от начала эксплуатации, т.е.
p(t)=P{Tіt}.
Перечислим некоторые очевидные свойства p(t):
1) p(0)=1, т.е. можно рассматривать безотказную работу лишь тех объектов, которые были работоспособны в момент включения;
2) p(t) является монотонно убывающей функцией заданной наработки t;
3) p(t)®0 при t®+Ґ, т.е. любой объект со временем откажет.
Наряду с p(t) используется функция ненадежности
q(t)=1-p(t)=P{T<t}.
Она характеризует вероятность отказа объекта на интервале (0,t). Функция ненадежности является функцией распределения случайной величины Т; эта функция иногда обозначается F(t).
Рис.1.2. Функции надежности p(t) и ненадежности q(t) объекта.
Во многих задачах в качестве показателя надежности используется вероятность безотказной работы – вероятность того, что в пределах заданной наработки не возникает отказа объекта. При этом обычно имеют в виду условную вероятность p(t1,t2) безотказной работы в течение наработки от t1до t2 при условии, что при t1 объект был работоспособным. Эту условную вероятность можно определить по функции надежности.
Рассмотрим два интервала (0,t1) и (t1,t2). Событие, состоящее в безотказной работе в течение интервала (0,t2), является совмещением двух событий:
1) объект безотказно работал на интервале (0,t1);
2) оставшись работоспособным к моменту t1 объект безотказно проработал на интервале (t1,t2).
Поэтому согласно правилу умножения вероятностей
p(t2)=p(t1)p(t1,t2),
следовательно,
p(t1,t2)= p(t2)/p(t1) (1.1)
Таким образом, условная вероятность безотказной работы на интервале (t1,t2) равна отношению значений функции надежности в начале и конце интервала.
Для малых интервалов времени значения p(t1,t2) будут близкими к единице. Об этом говорит сайт https://intellect.icu . Поэтому наряду с p(t) используются и другие показатели надежности, например плотность распределения наработки до отказа
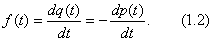
Плотность распределения наработки до отказа f(t) является дифференциальной формой закона распределения наработки до отказа. Плотность f(t) является неотрицательной функцией причем
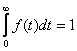
В соответствии с (1.2) функция надежности и функция ненадежности связаны с f(t) соотношениями

Величина f(t)dt характеризует вероятность отказа за интервал наработки (t,t+dt) объекта, взятого наугад из множества одинаковых объектов. При этом неизвестно, работоспособен ли этот объект к началу интервала (т.е. в момент t) или отказал ранее. Это не всегда удобно поэтому на практике чаще применяют интенсивность отказов l(t) – условную плотность вероятности возникновения отказа неремонтируемого объекта, при условии, что до этой наработки отказ не возник.
Условную вероятность отказа объекта в течение наработки (t,t+dt) в предположении его безотказной работы до момента t обычно выражают формулой
z=l(t)dt,
отказавшие объекты к моменту t из рассмотрения исключаются.
Причем

Решение уравнения (1.3) при начальном условии p(0)=1 дает для функции надежности формулу

При l=const формула (1.4) существенно упрощается:
p(t)=exp(-lt). (1.5)
В качестве показателей надежности неремонтируемых изделий применяют также числовые характеристики случайной наработки до отказа. Их обычно легче определить по эксперементальным данным, чем p(t), l(t),f(t). Наиболее часто используют среднюю наработку до отказа (математическое ожидание наработки до отказа).
Согласно определению математического ожидания непрерывной неотрицательной случайной величины, выполняя некоторые преобразования получим среднюю наработку до отказа
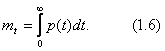
При l=const имеем:
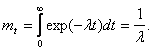
 Подставив в (1.5) значение t=mt=1/l, получим, что при l=const среднюю наработку до отказа можно понимать как наработку t=mt, в течение которой объект остается работоспособным с вероятностью p(mt)=exp(-1)»0.37
Подставив в (1.5) значение t=mt=1/l, получим, что при l=const среднюю наработку до отказа можно понимать как наработку t=mt, в течение которой объект остается работоспособным с вероятностью p(mt)=exp(-1)»0.37
Значения mt обычно вычисляются по эксперементальным
данным об отказах элементов в начальный период их эксплуатации.
На практике представляют интерес две условные средние
наработки неремонтируемых объектов:
1) средняя полезная наработка 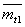 при условии, что при
при условии, что при
достижении наработки t1 все оставшиеся работоспособными
объекты снимаются с эксплуатации;
2) средняя продолжительность предстоящей работы 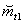
при условии что объект безотказно работал на интервале
(0,t1)
Причем mt=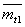 +
+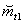 p(t1).
p(t1).
При l=const имеем: 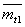 = mt[1-exp(-lt1)];
= mt[1-exp(-lt1)];
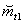 = mt=1/l.
= mt=1/l.
Это соотношение иллюстрирует рис.1.3
Статью про показатели надежности неремонтируемых объектов я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое показатели надежности неремонтируемых объектов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория надёжности
Из статьи мы узнали кратко, но содержательно про показатели надежности неремонтируемых объектов
Комментарии
Оставить комментарий
Теория надёжности
Термины: Теория надёжности