Сразу хочу сказать, что здесь никакой воды про надежность программ, и только нужная информация. Для того чтобы лучше понимать что такое надежность программ , настоятельно рекомендую прочитать все из категории Теория надёжности.

В современных АСУ, использующих цифровые ЭВМ, очень велико значение не только безотказной работы машин, но и программ, не имеющих скрытых ошибок. В настоящее время существует тенденция к снижению качества программ, увеличению количества ошибок в них.

Современные методы разработки и проверки программ не обеспечивают создания оптимальных программ даже при известных путях их улучшения. В практике программирования разработчику обычно трудно оценить несколько возможных решений, так как проверка программы часто возможна лишь после объединения ее частей, когда изменения в программе связаны со значительными затратами времени и средств. Кроме того, часто используются ранее составленные блоки программ, что также затрудняет оптимизацию данной программы. Не все блоки программируются одинаково тщательно и подробно, часто теряется однородность написания различных блоков. Это обнаруживается обычно слишком поздно.

Понятие ошибка программы можно определить как несоответствие между данной и некоторой “идеальной” программами. Однако, если бы “идеальная” программа существовала, не было бы проблемы. Поэтому, чтобы использовать математический аппарат теории надежности, рассматривают отказы программы–события, состоящие в переходе к неверной работе или остановке программы. После появления отказа программисты исследуют программу с целью поиска (локализации) ошибки и усовершенствования программы.

Сведения об ошибках и их исправлении выдаются на специальных извещениях. Ошибка считается исправленной, если при проведении повторного теста ошибка не обнаружена и выпущено дополнение к извещению о наличии ошибки. Время от выпуска извещения об ошибке до выпуска дополнительного извещения называется циклом отладки.

По сложности программы можно разделить на несколько типов.

Длина стандартных программ для вычисления элементарных функций не превышает сотни команд. Эти программы проверяются очень тщательно, но иногда в них обнаруживаются ошибки, обычно при специфических значениях аргумента. Проводка стандартных программ не представляет затруднений.

Более сложными программами являются трансляторы, которые применяются для преобразования алгоритмов, записанных на языке программирования в последовательность машинных команд. Трансляторы содержат 10000–50000 команд. Полную проверку транслятора обычно не удается осуществить, поэтому в процессе эксплуатации продолжается выявление ошибок.

Наиболее сложными являются программы управления в реальном масштабе времени, реализуемые на вычислительных машинах с мультипроцессором (содержат сотни тысяч команд). Полная проверка таких программ в процессе отладки невозможна. Функционирование программы может быть полностью оценено лишь в процессе применения. Ошибки программ обычно проявляются только при действии определенных входных сигналов, которые в данном случае играют роль условий работы программ.

При рассмотрении множества значений входных сигналов, ошибки программ могут считаться случайными.

4.1. Особенности оценки надежности программ

Время эксплуатации программы представляет собой последовательность чередующихся периодов наработки T(i) от момента восстановления до отказа программы и времени восстановленияот момента отказа до момента восстановления, т. е. внесения в программу исправлений.

Аналогичная модель рассматривается при оценке надежности восстанавливаемых изделий, причем все случайные величины T(i) считаются одинаково распределенными (аналогично и). При этом используются математические модели теории восстановления.

Непосредственное применение этих моделей для оценки надежности программ нецелесообразно из-за ряда особенностей случайного процесса их эксплуатации.

Во-первых, периоды наработки между отказами T(i) имеют тенденцию к увеличению с течением времени эксплуатации. Это связано с тем, что по мере выявления и устранения ошибок их общее количество в программе уменьшается, поэтому отказы программ становятся все более редкими.

Процесс совершенствования управляющих программ можно рассматривать как процесс выявления и устранения скрытых дефектов.

Существует также тенденция к уменьшению времени восстановления, так как у программистов все время накапливается соответствующий опыт. Вместе с тем можно предположить взаимную независимость случайных векторов TиTв.

Во-вторых, большие управляющие программы обычно являются уникальными. Если для технических изделий оценки показателей надежности обычно вычисляются по статистическим данным об отказах и восстановлениях многих однотипных изделий, то при оценке надежности программ возможно лишь индивидуальное прогнозирование. Большие программы начальный период эксплуатации обычно работают в одном экземпляре и лишь после выявления и устранения подавляющего большинства ошибок, т. е. при достижении определенного уровня надежности, могут в редких случаях тиражироваться. Поэтому метод оценки надежности программ должен предусматривать период накопления экспериментальных данных с последующим экстраполированием значений показателей надежности программ. Период накопления данных должен быть сравнительно небольшим. Поэтому на практике можно получить не более двух первых моментов случайных величин.

Таким образом, для оценки надежности программ необходима новая, не применявшаяся ранее в теории надежности математическая модель потока случайных событий (отказов и восстановлений).

4.2. Оценка безотказности программ по наработке

Наработку между очередными отказами — случайную величину можно представить в виде суммы двух случайных величин:

(4.1)

Последовательно применяя (4.1) ко всем периодам наработки между отказами, получаем:

(4.2)

Случайная величина Тn – наработка до возникновенияn–го отказа программы равна

(4.3)

Введем следующие допущения:

1) все случайные величины 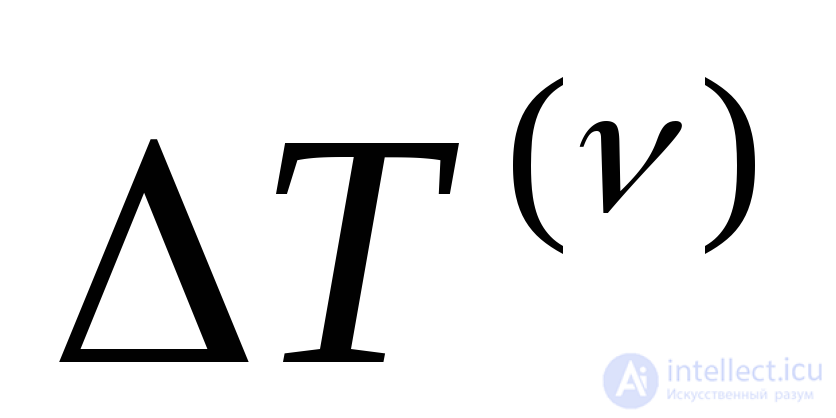независимы и имеют одинаковые математические ожидания и средние квадратические отклонения ;

2) случайная величина 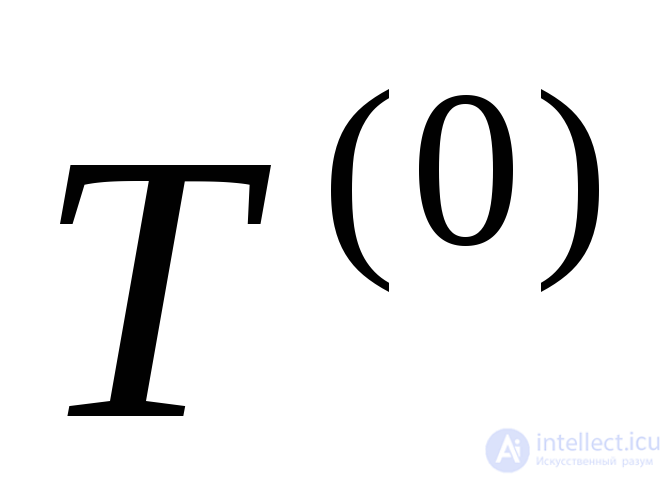пренебрежимо мала по сравнению с суммой

Основанием для второго допущения могут служить следующие соображения. В самый начальный период эксплуатации программы ошибки возникают очень часто, т. Об этом говорит сайт https://intellect.icu . е. время мало. Сумма (5-24) быстро растет с уве­личением n, и доля быстро падает. Будем считать .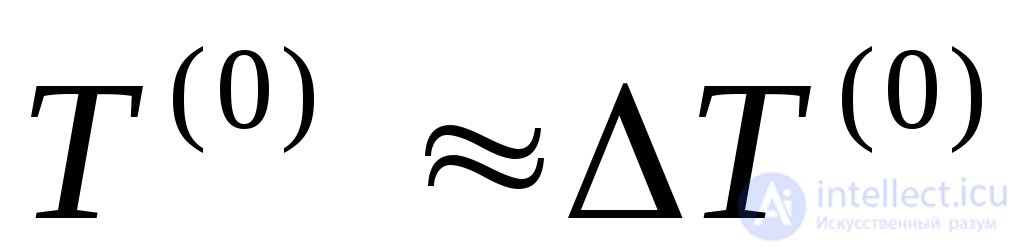

В соответствии со вторым допущением из (4.2) имеем:

(4.4)

(4.5)

При одинаковых наработка между (п- 1)-м и n-м отказами — случайная величина Т(n) — имеет матема­тическое ожидание

(4.6)

и среднее квадратическое отклонение

(4.7)

Для случайной величины Тп математическое ожида­ние

(4.8)

и среднее квадратическое отклонение

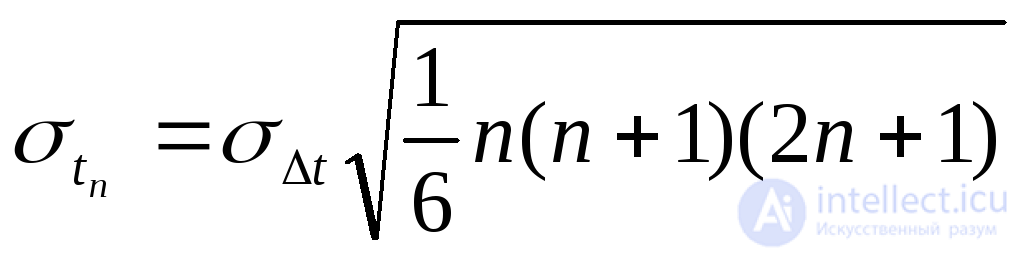(4.9)

Чтобы вычислить значения 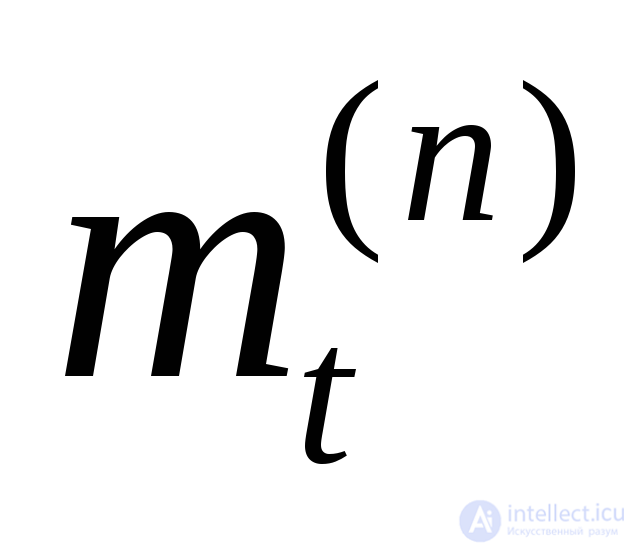, 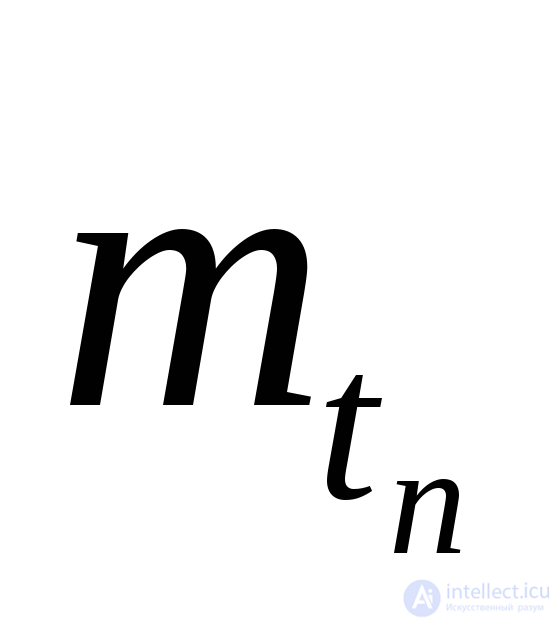и 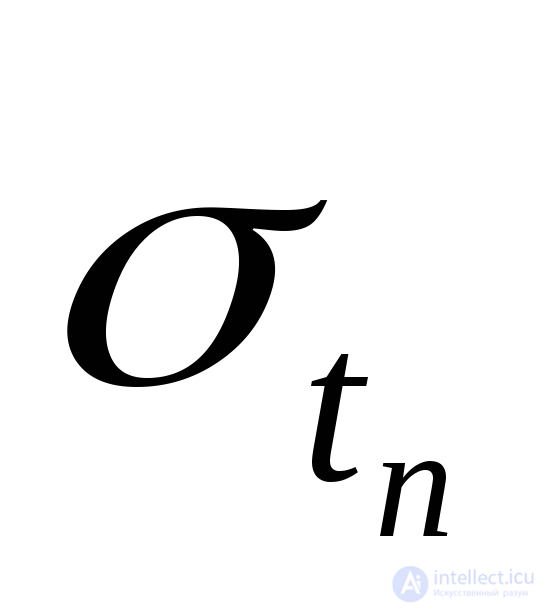, необходимо по данным об отказах программы в течение периода на­блюдения tH найти статистические оценки числовых ха­рактеристик случайной разности

(4.10)

(4.11)

где nн - число отказов программы за наработку (0, tн).

Учитывая, что при t> tн число отказов nн >1, из (4.8) и (4.9) имеем:

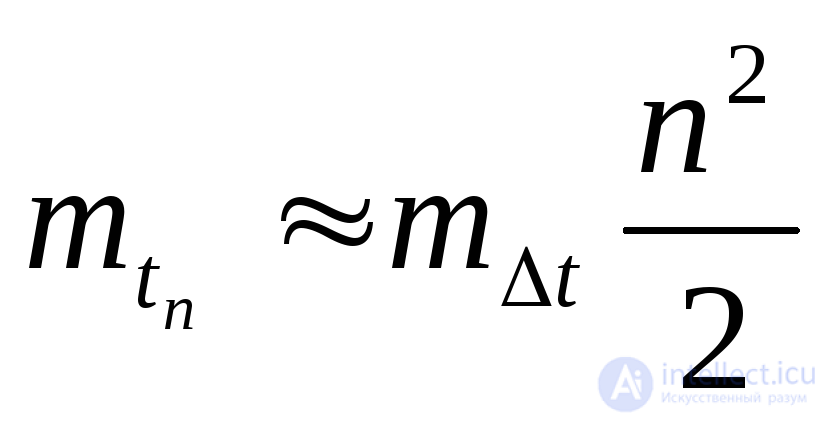(4.10)

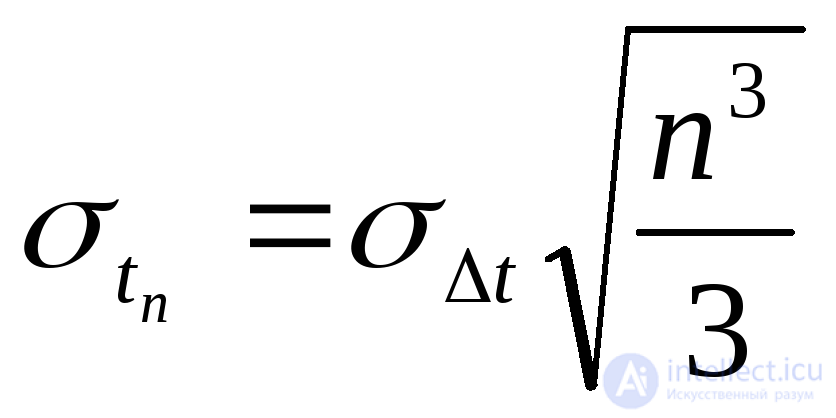(4.11)

Поскольку случайные величины T(n) и Tn согласно (4.4) и (4.5) равны суммам многих случайных вели­чин T(n) и Tn можно считать распределенными нормаль­но c математическими ожиданиями и дисперсиями, опре­деленными по (4.6) — (4.9), (4.10) и (4.11). Так как наработка положительна, на практике используется усе­ченное на интервале (0, ∞) нормальное распределение. Обычно нормирующий множитель с≈1.

При п>nH плотность распределения наработки между очередными (п-1)-м и п-м отказами

где τ отсчитывается с момента последнего, (п—1)-го отказа.

Соответствующая функция распределения наработки между отказами

,

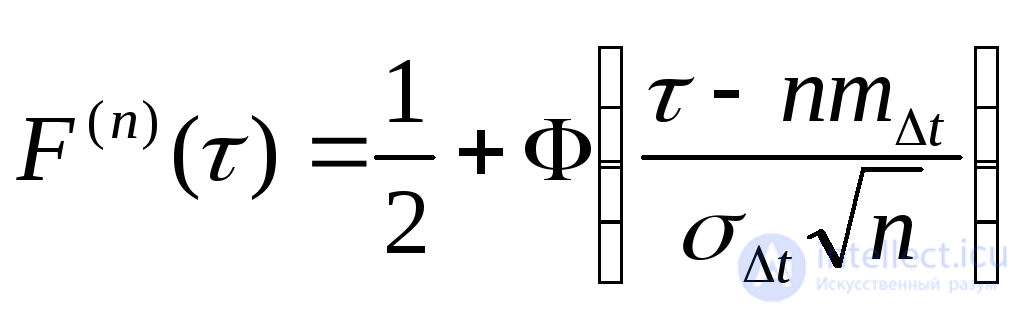где 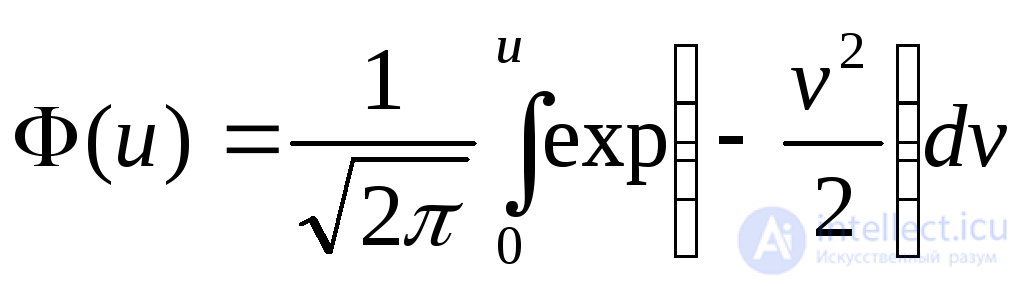- табулированная функция.

При вычислении вероятности безотказной работы программы удобно использовать условную функцию надежности (вероятность того, что случайная наработка до отказа будет больше заданной наработки, отсчитывае­мой с момента последнего (п-1)-го отказа).

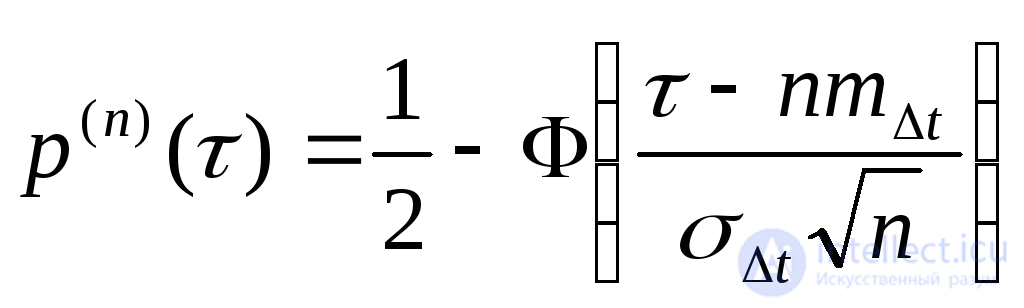(4.12)

В соответствии с (4.12) вероятность безотказной работы в течение заданной наработки 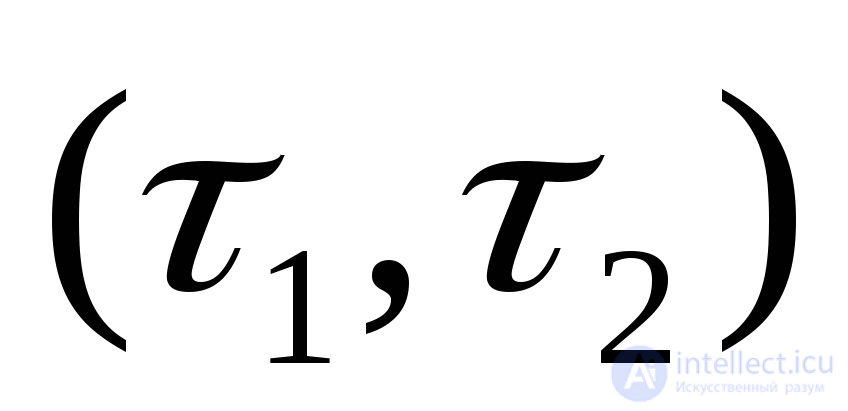после (п-1) – го отказа

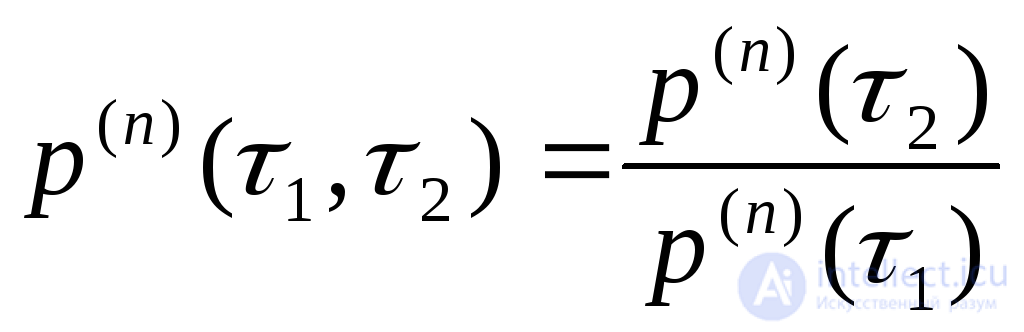(4.13)

При сделанных выше допущениях отказы программы образуют редеющий случайный поток. Ведущая функция потока, т. е. среднее число отказов, происшедших за ин­тервал наработки (0, t), при t>tн

(4.14)

где Fn(t) — функция распределения наработки до появ­ления n-го отказа.

Параметр потока отказов программ (вычисляется по наработке)

(4.15)

где

— плотность распределения наработки до появления п-го отказа.

Из (4-15) имеем выражение для параметра потока отказов программы при t>tн

(4.16)

График функции ω(t) является слегка волнистой кри­вой с убывающими максимумами при значениях

, гдеп= nн ,пн+1, . . .

Ввиду сложности выражений (4.14) и (4.16) целесо­образно аппроксимировать их более простыми приближенными формулами. Практически имеет смысл приме­нить метод наименьших квадратов. В соответствии с этим методом аппроксимирующая функция [для ω(t) целесообразно взять Aexp(-vt)] наилучшим образом согласуется на интервале (tH, t1) с функцией, определяемой выражением (5-39), при выполнении условия

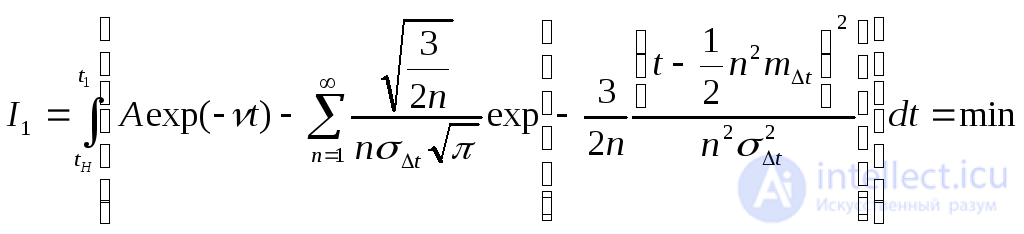(4.17)

Приравняв нулю частные производные интеграла I1 по A и v, получим систему уравнений для определения этих числовых характеристик. Аналогично можно посту­пить при аппроксимации Q(t) функцией 1-Вехр(-γi).

4.3. Оценка готовности программ

При оценке готовности рассмотрим процесс восста­новления работоспособности программы (в календарном времени). Наработка между очередными восстановле­ниями работоспособности программы

, (4.18)

где 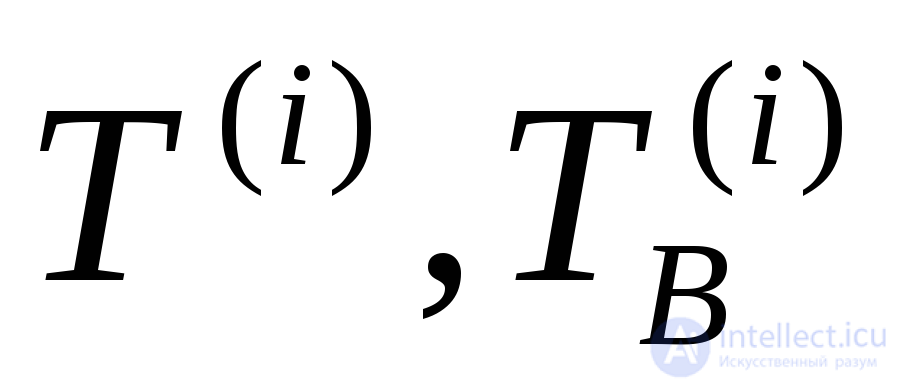- независимые случайные величины.

Величина определена согласно (4.2). Учитывая накопление опыта восстановления программы, величи­ну можно представить в виде

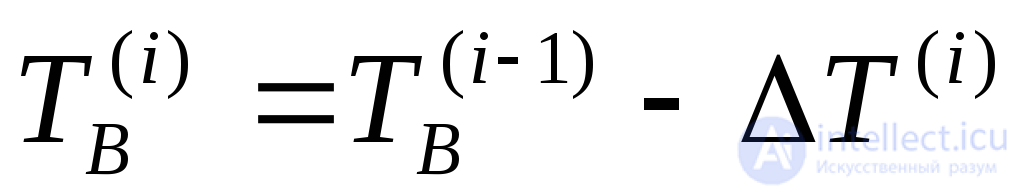(4.19)

Последовательно применяя (4.19) ко всем очередным восстановлениям, получаем:

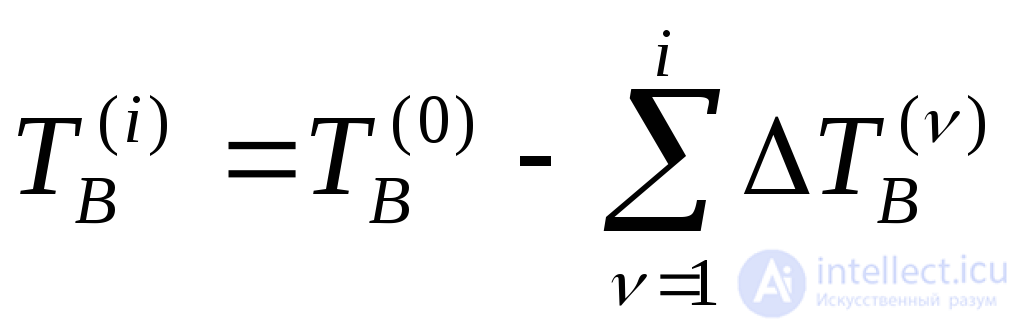(4.20)

Подставив выражения для 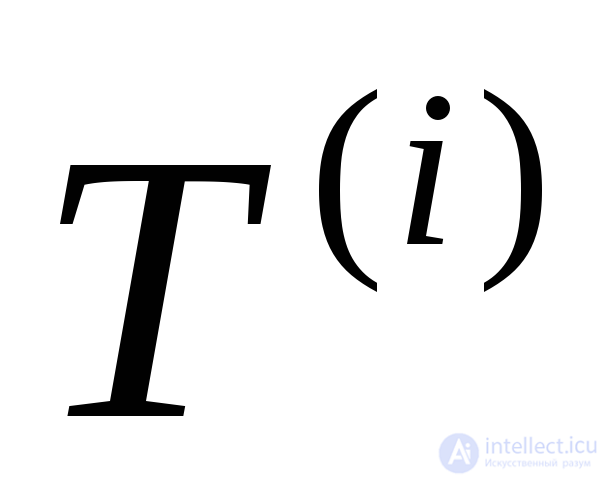и согласно (4.2) и (4.20) в (4.18), получим:

.

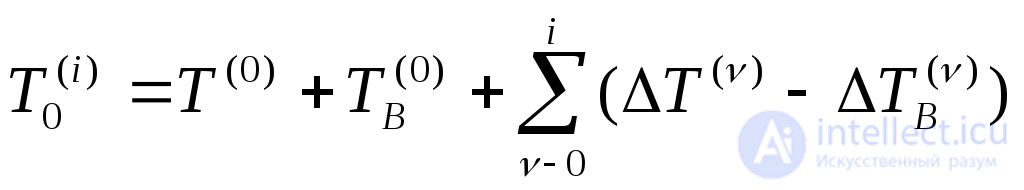Случайная величина T0 п - наработка до возникнове­ния п-го отказа программы:

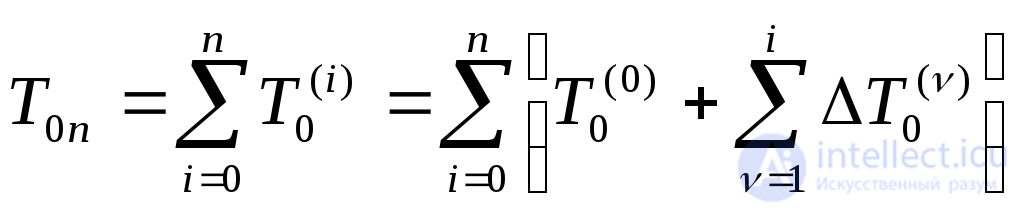(4.21)

где обозначено:

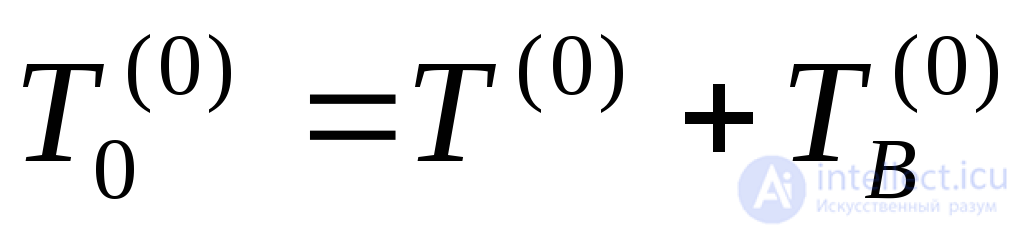; (4.22)

. (4.23)

Введем допущения, аналогичные приведенным выше при рассмотрении безотказности программы. Предположим независимость 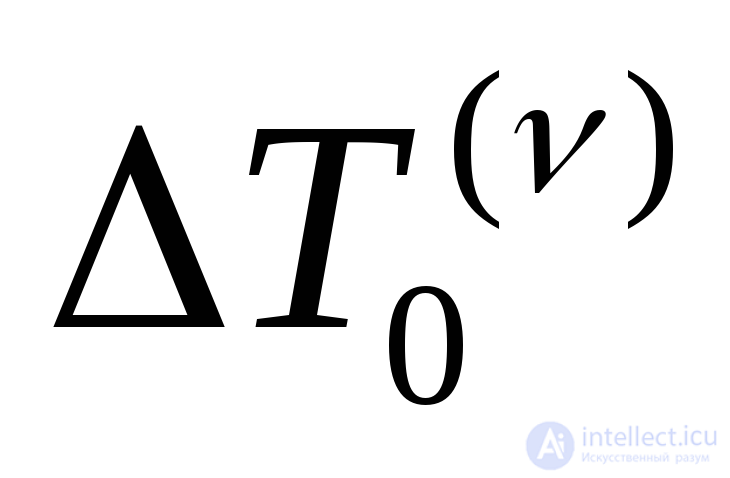, одинаковость их математических ожиданий и дисперсий и малость по сравнению с суммой при больших v. Кроме того, учтем, что обычно должно быть . Положив ,получим:

(4.24)

При одинаковых случайная величина имеет математическое ожидание

; (4.25)

среднее квадратическое отклонение

, (4.26)

где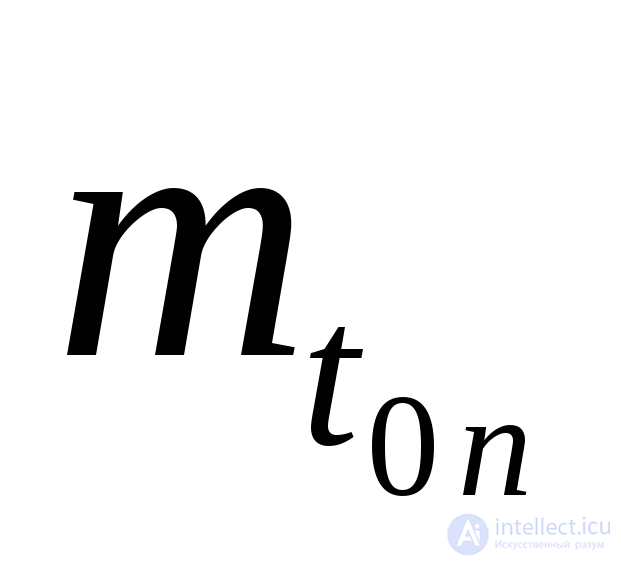, - математическое ожидание и среднее квадратическое отклонение .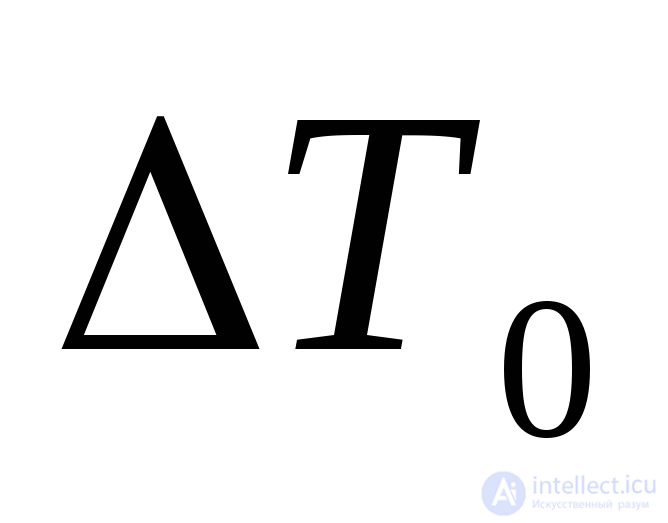

Учтя, что в соответствии с (4.22), (4.23)

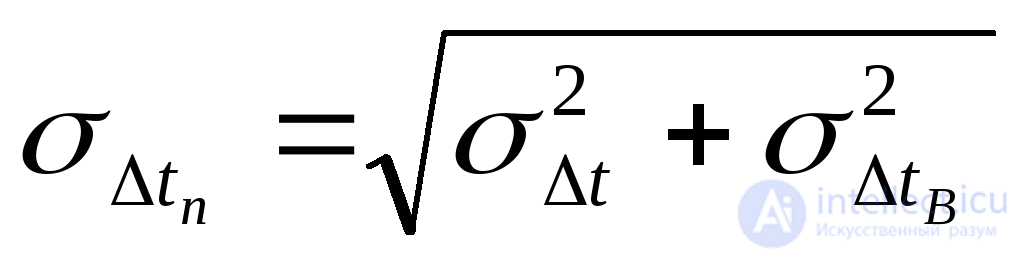
получим:

(4.27)

(4.28)

При п>>1

(4.29)

(4.30)

Значения 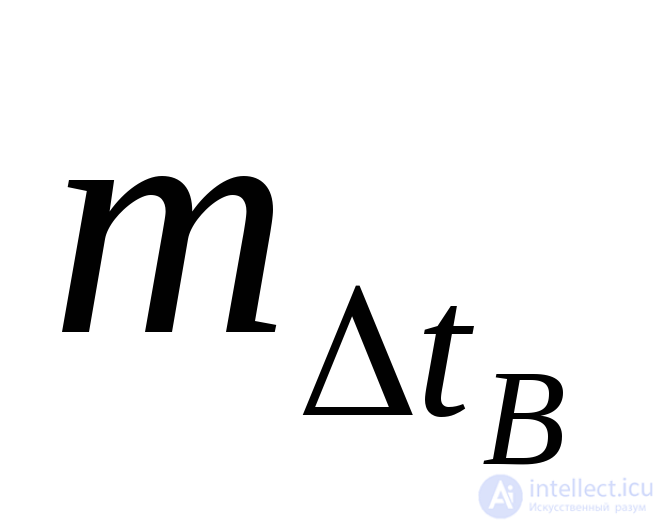и оцениваются по статистическим данным о времени восстановления (устранения ошибки) программ аналогично значениям и .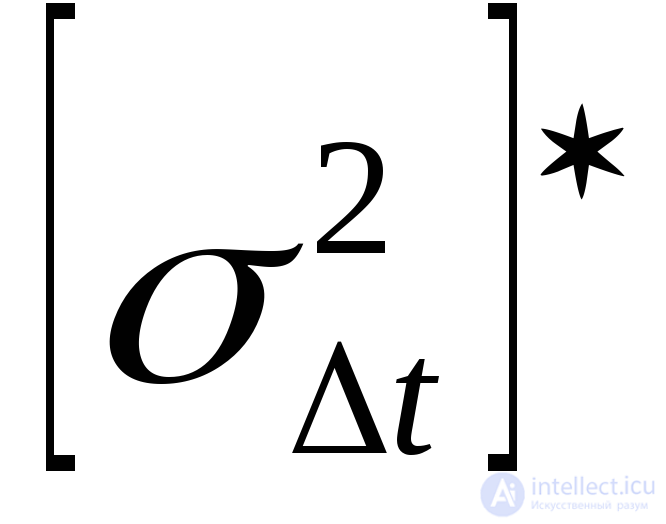

Вычислив и, можно найти параметр потока восстановлений

(4.31)

где 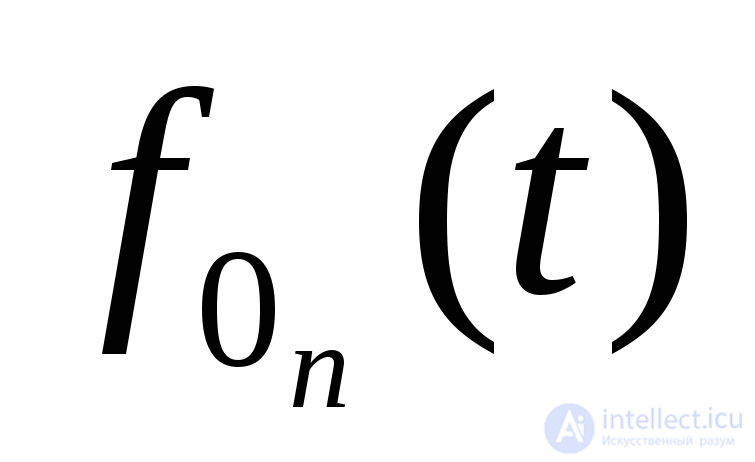- плотность распределения времени появления п-го восстановления.

Функция готовности Г(t) (выражает вероятность нахождения программы в работоспособном состоянии в мо­мент времени t) равна вероятности суммы несовместных событий

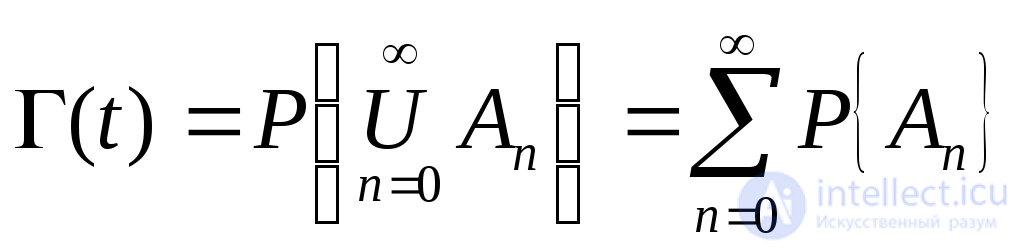(4.32)

где каждое событие Ап состоит в том, что до момента t произошло n отказов и восстановлений и в момент t программа работоспособна.

Для определения вероятности появления события Ап рассмотрим малый интервал (θ, θ + d θ), предшествую­щий t. Вероятность того, что на этом интервале закончится последнее n-с восстановление и программа боль­ше не откажет за оставшееся время (t— θ), равна:

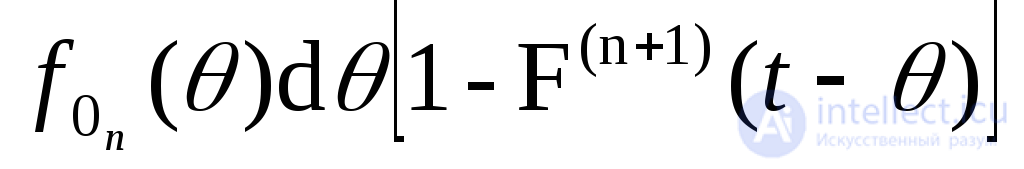
где 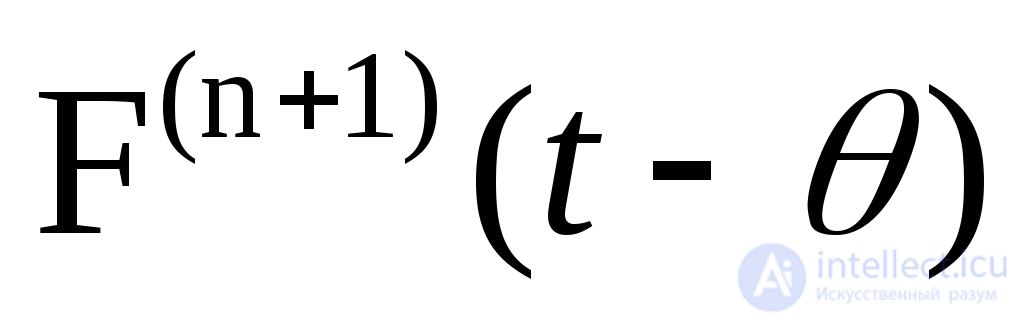- функция распределения времени меж­ду окончанием n-го восстановления и (n + 1)-м отказом.

Интегрируя по θ от 0 до t, имеем:

Подставляя выражение для вероятности в фор­мулу (4.32), получаем:

(4.33)

Учитывая, что практическое значение имеют лишь значения t>tn, когда произошло уже несколько десятков отказов, имеем:

(4.34)

Подставив в (4.34) выражения для , 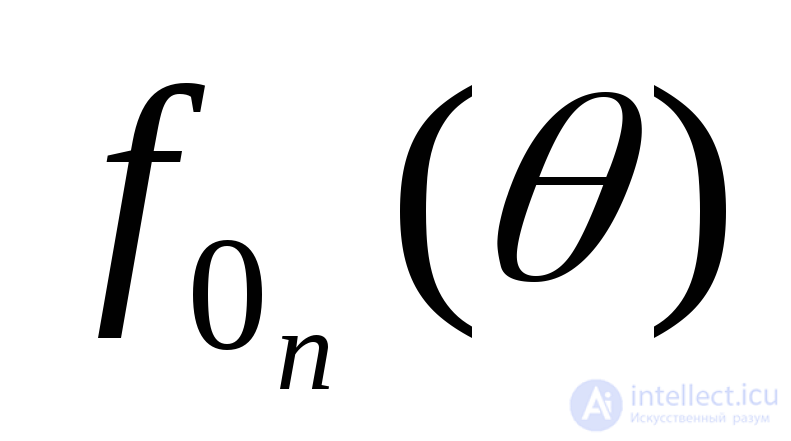и учтя, что , получим:

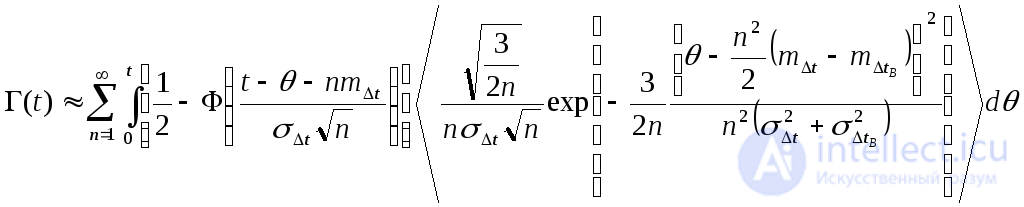(4.35)

Из постановки задачи очевидно, что при зна­чения. Сложное выражение (4.35) целесообраз­но аппроксимировать простой приближенной формулой, напримерF(t) = 1 - Сехр(-δt), подобрав С и δ с по­мощью метода наименьших квадратов аналогично (4.17).

Таким образом, для практического применения можно будет использовать простые формулы, учитывающие со­вершенствование программ и обучение персонала.

Вопросы для самоконтроля:

1. Дать определение понятию ошибка программы.

2. На какие типы по сложности можно разделить программы?

3. Что такое время эксплуатации программы?

4. Особенности оценки надежности программ?

5. Привести формулу вычисления вероятности безотказной работы программы.

6. Что такое оценка готовности программы?

7. Привести формулу математического ожидания и среднеквадратического отклонения.

8. Что такое функция готовности программы?

А как ты думаешь, при улучшении надежность программ, будет лучше нам? Надеюсь, что теперь ты понял что такое надежность программ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория надёжности

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.