Сразу хочу сказать, что здесь никакой воды про экономическая эффективность и надёжность асу, и только нужная информация. Для того чтобы лучше понимать что такое экономическая эффективность и надёжность асу , настоятельно рекомендую прочитать все из категории Теория надёжности.

Как уже подчеркивалось, одной из основных целей разра­ботки промышленных АСУ является получение чисто эко­номического эффекта.

Следует подчеркнуть, что оценка экономической эффек­тивности АСУ на ранних этапах ее разработки (составление технического задания, разработка технического и рабочего проектов) значительно важнее, чем на этапе внедрения, по­скольку здесь решаются такие вопросы, как целесообраз­ность вообще разрабатывать данную систему, выбор варианта ее структуры, компоновки и комплектации.

Таким образом, методы расчета показателей экономиче­ской эффективности АСУ играют очень важную роль.

Однако существующие методы обладают большим не­достатком: их выполняют без учета надежности функциони­рования АСУ, а она самым существен­ным образом влияет на показатели экономической эффек­тивности .

Помимо задачи оценки показателей экономической эф­фективности с учетом надежности на этапе разработки АСУ возникает еще одна задача, в которой тесно связаны пока­затели экономической эффективности и надежности,— опре­деление оптимальных требований к надежности АСУ по критерию максимума экономической эффективности.

5.1. Показатели экономической эффективности промышленных объектов. Экономические критерии оптимизации технических решений

Для сравнения по экономической эффективности различных объектов (или вариантов реализации одного и того же объекта) необходимы количественные показатели. Такое сравнение чаще всего выполняют следующим обратом: 1) получают автономные показатели экономической эффек­тивности сравниваемых объектов (или вариантов); 2) со­поставляют полученные показатели и выносят решение. Эти показатели удобно назвать внутриобъектными. К ним относятся, например, коэффициент экономической эффек­тивности объекта, срок окупаемости, приведенные затраты на единицу выпускаемой продукции и т. п.

Возможен, вообще говоря, и иной путь сравнения двух объектов. Взяв определенные экономические характери­стики двух сравниваемых объектов, можно рассчитать не­который результирующий показатель, определяющий ве­личину эффективности одного объекта по сравнению с дру­гим. Такие показатели называют межобъектными. Примером может служить годовой экономический эффект от замены одного объекта другим.

Второй путь сравнения методически значительно усту­пает первому, потому что здесь возможно лишь попарное сравнение объектов и если затем потребуется сравнить один из этих объектов с некоторым третьим, то нужно вновь вычислять соответствующий межобъектный показатель. При сравнении первым путем получают показатели абсолютной эффективности всех сравниваемых объектов.

В качестве основного показателя общей (абсолютной) экономической эффективности отдельных объектов и техни­ческих мероприятий принят коэффициент экономической эффективности капитальных вложений:

Эк.п=П/К (5.1)

где К — капитальные вложения (капитальные затраты) в рассматриваемый объект или техническое мероприятие в АСУ); П — годовая прибыль, обеспечиваемая этими капитальными вложениями.

Если рассматриваются капитальные вложения в само­стоятельные объекты, величина годовой прибыли может быть представлена в виде

П=Ц-С (5.2)

где Ц — стоимость (в оптовых ценах) годового выпуска продукции рассматриваемым объектом; С – себестоимость годового выпуска продукции.

Если же рассматриваются капитальные вложения в ме­роприятия, являющиеся усовершенствованием некоторых действующих объектов, в том числе в АСУ, то, во-первых, прибыль от введенного мероприятия представляет собой разность между прибылью от усовершенствованного объекта и прибылью, обеспечиваемой им до введения усовершенство­вания; во-вторых, в общем случае вводимое усовершенство­вание может оказать влияние как на стоимость, так и на себестоимость годового выпуска продукции. В связи с этим коэффициент экономической эффективности

Эк.п = ∆П/К = (П2-П1)/К = [(Ц2 - С2) - (Ц1 - С1)]/К = [(Ц2 – Ц1) + (С1 – С2)]/К (5.3)

где П1 и П2, Ц1 и Ц2, С1 и С2 — годовая прибыль, стоимость и себестоимость годового выпуска продукции объекта соответственно до и после введения усовершенствования.

В обоих случаях физический смысл коэффициента Эк.п остается одним и тем же — это отношение прибыли, обу­словленной некоторыми капитальными вложениями, к их величине. Другими словами, Эк.п — это показатель степени отдачи капитальных вложений. Следовательно, во-первых, по величине Эк.п можно сравнивать любые объекты (и усо­вершенствования). Во-вторых, при вычислении Эк.п для различных объектов нет необходимости уравнивать объемы выпускаемой продукции. В-третьих, как следует из формулы (5.3), источником прибыли, учи­тываемой при вычислении Эк.п для мероприятий, направлен­ных на усовершенствование действующих объектов, может служить как снижение себестоимости выпускаемой продук­ции, так и увеличение годового объема выпуска и улучше­ние качества. В последнем случае, однако, необходимо, чтобы это улучшение нашло отражение в оптовой цене про­дукции.

При определении экономической эффективности АСУ, разрабатываемой для действующего объекта, следует рас­сматривать АСУ как некоторое усовершенствование и поль­зоваться формулой (5.3).

С коэффициентом Эк.п однозначно связан еще один показатель общей (абсолютной) экономической эффективности капитальных вложений — срок окупаемости капитальных вложений:

Ток=1/ Эк.п = К/П (5.4)

Следует отметить, что срок окупаемости капитальных вложений в усовершенствования действующих объектов в не­которых методиках предлагается рассчитывать по формуле

Ток=К/(С1-С2) (5.5)

При этом предполагается, что вводимое усовершенствование не влияет ни на объем годового выпуска продукции, ни на ее качество (т. е. цену), а дает лишь снижение себестоимости с величины С1 до величины С2. Нетрудно видеть, что фор­мула (5.5) есть частный случай более общего выражения (5.4). Таким образом, понятие срока окупаемости, позволяет учитывать влияние произ­водимых усовершенствований как на себестоимость годово­го выпуска продукции, так и на ее объем и качество (цену), и потому является более общим, чем понятия, использовав­шиеся ранее.

Для сравнения по экономической эффективности раз­личных вариантов хозяйственных или технических решений, вариантов реализации промышленных объектов и отдельных мероприятий

введем в качестве количе­ственного показателя приведенные затраты на некоторый фиксированный объем (V) годового выпуска продукции:

У=У(V)=С + ЕнК, (5.6)

где Ен — нормативный коэффициент экономической эффек­тивности, принимающий различные значения для разных отраслей народного хозяйства и устанавливаемый на уров­не не ниже 0,12, что соответствует нормативному сроку оку­паемости Ток.н = 8,33 года.

Величина приведенных затрат может вычисляться также на единицу выпускаемой продукции:

У0=У(1)=У(V)/V = C0+ЕнК0 (5.7)

где С0 и К0 — соответственно удельная (в расчете на еди­ницу продукции) себестоимость и удельные капитальные вложения.

Существенным преимуществом У по сравнению с Эк.п является то, что для расчета У не требуется знать цену еди­ницы выпускаемой продукции. С этим преимуществом свя­зан и основной недостаток показателя приведенных затрат: он может использоваться для сравнения только таких объектов, которые выпускают совершенно идентичную продук­цию, и не позволяет учесть, в частности, изменение каче­ственных показателей продукции. Стремясь обойти это ограничение, иногда в расчет величины приведенных затрат вводят специальные коэффициенты для учета из­менения качественных показателей выпускаемой продукции. Однако выбор величины этих коэффициентов всегда очень трудно обосновать.

Рассмотрим некоторые особенности применения показа­теля приведенных затрат в случае, когда рассматривается мероприятие по усовершенствованию действующего объек­та (в частности, АСУ). При этом под капитальными затрата­ми (К) следует понимать сумму затрат на сам объект (Коб) и проводимое усовершенствование (∆К). Себестоимость вы­пускаемой продукции определяется для объекта с введен­ным усовершенствованием; обозначим ее через С2 в отличие от себестоимости той же (по объему и качеству) продукции на исходном объекте, которую будем обозначать через С1. Таким образом,

У2 = С2 + Ен (Коб+∆К). (5.8)

Для того, чтобы предлагаемое усовершенствование было эф­фективно, необходимо выполнение неравенства

У2<У1 (5.9)

ИЛИ

С1-С2<Ен∆К (5.10)

Как уже отмечалось выше, величина приведенных за­трат, которая вычисляется для каждого объекта отдельно, относится к внутриобъектным показателям.

Производным от показателя приведенных затрат явля­ется годовой экономический эффект от замены одного объек­та (действующего или проектируемого) другим либо внед­рения некоторого предлагаемого усовершенствования или мероприятии я:

Э=(У01-У02)V2=[(С01=ЕнК01)-( С02=ЕнК02)]V2 (5.11)

где V2 — объем годового выпуска продукции по предлагае­мому объекту (или варианту).

Очевидно, что годовой экономический эффект является межобъектным экономическим показателем и имеет смысл лишь при наличии двух сравниваемых вариантов (пред­лагаемого и того, который является «базой сравнения»).

Еще одним межобъектным показателем может служить так называемый коэффициент прогрессивности техническо­го решения:

γн= Эк.п2/Эк.п1 (5.12)

Введенные выше основные показатели экономической эффективности позволяют сформулировать следующие два экономических критерия сравнения (оптимизации) технических решений:

Эк.п→max (5.13)

У0→min (5.14)

Естественно ожидать совпадения результатов сравнения различных вариантов технических решений одной и той же задачи по экономическим критериям (5.13) и (5.14). К сожалению, однако, природа этих критериев такова, что результаты не совпадают.

Пример 1. Пусть проводится сравнение двух вариантов исполне­ния некоторого промышленного объекта, характеризующихся при прочих равных условиях следующими показателями:

Ц1 = 630 тыс. руб., С1 = 420 тыс. руб., К1 = 1000 тыс. руб.;

Ц2 = 900 тыс. руб., С2 = 180 тыс. руб., К2 = 4000 тыс. руб.

Цена единицы выпускаемой продукции в обоих вариантах одинакова; примем ее равной Ц0=1,5 тыс. руб. В соответствии с этим годовой объем выпуска продукции в первом варианте равен V1 =Ц1/Ц0 = 420 шт., во втором V2 =Ц2/Ц0 = 600 шт.

Сравнение по Эк.п дает для рассматриваемых вариантов

Эк.п1 = 0,21 > Эк.п2 = 0,18

а сравнение по У0 при ЕН = 0,12

У01 = 1,29 > У02 = 1,1

Таким образом, по критерию (5.13) лучшим является первый вариант, а по критерию (5.14) — второй.

Покажем, что сравнение по критериям (5.13) и (5.14) в принципе способно давать противоречивые результаты.

Пусть для двух сравниваемых вариантов некоторого про­мышленного объекта известны V1, С1, К1 и V2, С2, К2. Це­на единицы выпускаемой продукции в обоих случаях оди­накова и равна Ц0.

Коэффициенты экономической эффективности сравнивае­мых вариантов:

Эк.п1=(V1Ц0-С1)/К1 Эк.п2=(V2Ц0-С2)/К2 (5.15)

(пусть Эк.п1 > Эк.п2)

Для сравнения по приведенным затратам необходимо прежде всего уравнять объемы выпуска продукции. Выбрав расчетный объем выпуска продукции Vрасч и введя коэффнциенты

α1= Vрасч /V1 α2= Vрасч /V2

из формулы (5.15) получим:

Эк.п1 = (α1V1Ц0 - α1С1)/α1К1 (5.16)

Эк.п2 = (α2V2Ц0 - α2С2)/α2К2 (5.17)

Введя обозначения

α1V1Ц0 = х1, α2V2Ц0 = х2

находим:

х1 = α1С1 + Эк.п1 α1К1 (5.18)

х2 = α2С2 + Эк.п2 α2К2 (5.19)

В координатах Эк.п1, х это уравнения двух прямых, от­секающих на оси х отрезки α1С1 и α2С2 и пересекающихся в точке с абсциссой

Эк.пкр = (α2С2 - α1С1)/( α1К1 – α2К2) (5.20)

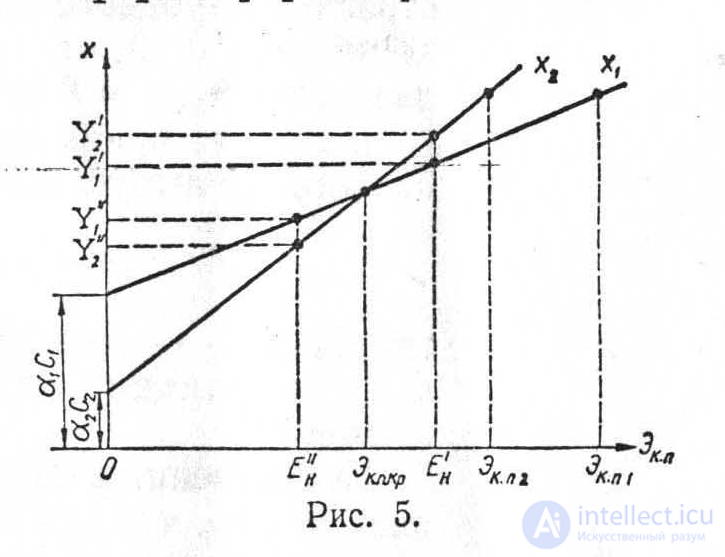
Графики х1 = f1(Эк.п1) и х2 = f2(Эк.п2) приве­дены на рис. 5 (ввиду Эк.п1 > Эк.п2 прямая х2 идет круче).

Из смысла введенных коэффициентов α1 и α2 следует, что

х1(Эк.п1)= х2(Эк.п2) = VрасчЦ0 (5.21)

Из сопоставления (5.18) и (5.19) с выражением (5.5) ясно, что

х1(Ен) = У1(Vрасч) и х2(Ен) = У2(Vрасч). (5.22)

Из приведенного на рис. 5 построения следует, что при данном соотношении Эк.п1 Эк.п2 результат сравнения ва­риантов по У зависит от взаимного расположения Эк.п1, Эк.п2 Эк.п.кр и Ен на оси абсцисс. Так, если Эк.п1, Эк.п2 и Ен (Ен’ рис. 5) лежат по одну сторону от Эк.п.кр, то результаты сравнения по Эк.п и У будут совпадать (У2’ > У1’). Если же Эк.п1 и Эк.п лежат по одну сторон от Эк.п.кр, а Ек — по другую (Ек” на рис. 5), результаты сравнения будут противоположными (У1 > У2)

В связи с неэквивалентностью критериев (5.13) и (5.14) при исследовании конкретного объекта перво­степенное значение приобретает вопрос о выборе основ­ного показателя экономической эффективности и соот­ветствующего ему критерия оптимизации технических ре­шений (в том числе и решений, связанных с уровнем надежности объекта). Нужно сказать, что четких рекомендаций по этому вопросу в экономической литературе нет. По мне­нию автора, эти рекомендации могут быть сведены кратко к следующему. Если рассматривается объект, предназна­ченный для выпуска продукции широкого потребления, и основным является извлечение максимальной прибыли на вкладываемые средства, то следует пользоваться критери­ем (5.13), соответствующим минимальному сроку окупае­мости капитальных вложений. Если же рассматриваемый объект предназначен для выпуска продукции, необходимой народному хозяйству, то должен использоваться критерий (5.14), позволяющий выбрать вариант решения поставлен­ной задачи с минимальной затратой общественных средств.

5.2. Расчет показателей экономической эффективности с учетом надежности.

Формулы (5.1)-(5.6) остаются в силе независимо от того, хотим мы вести расчет показателей экономической эффективности без учета или с учетом надежности. Характер расчета зависит только от того, как определены входящие в эти формулы величины К,П,Ц,С,и др.- с учетом надежности или без него.

Наша задача состоит в том, чтобы выразить их через показатели надежности и привести расчетные формулы к виду, удобному для практического применения. При этом условимся обозначать показатели экономической эффективности и используемые при их расчете величины, определенные с учетом надежности, соответствующими буквами со штрихом. Тогда стоимость годового выпуска продукции на рассматриваемом объекте с учетом надежности его функционирования *:

Ц’=Ц0V’= Ц0(V-Vсн.пр.) (5.23)

где V’- годовая производительность объекта с учетом надежности;V– годовая производительность объекта при абсолютной надежности;Vсн.пр – объем продукции, на который снижается годовая производительность объекта в связи с отказами.

Величина Vсн.пр является случайной и зависит от числа отказов объекта, имевших место в текущем году. В связи с этим в дальнейшем будем пользоваться величиной-математическим ожиданием указанной случайной величины. Соответственно этому и вместо величиныЦ’, которая также является случайной, введем величину.

Определение величины сопряжено с известными трудностями, поскольку она зависит от интенсивности отказов, и от степени их влияния на удельную (часовую) производительность объекта. Пусть максимальная производительность объекта в состоянии полной работоспособности равнаV0 , и пусть он имеетlсн.пр. видов отказов, в каждом из которых его производительность снижается до величины.

* Предполагается, что ненадежность объекта не сказывается на качестве и, следовательно, цене единицы выпускаемой продукции, о потому уменьшение стоимости годового выпуска в следствие ненадежности объекта обуславливается только снижением его годовой производительности.

Тогда годовая производительность объекта:

(5.24)

где - среднее время пребывания объекта в течение года вi-ом отказовом состоянии.

Ясно, что:

(5.25)

где - полное время эксплуатации объекта в течение года.

Величины 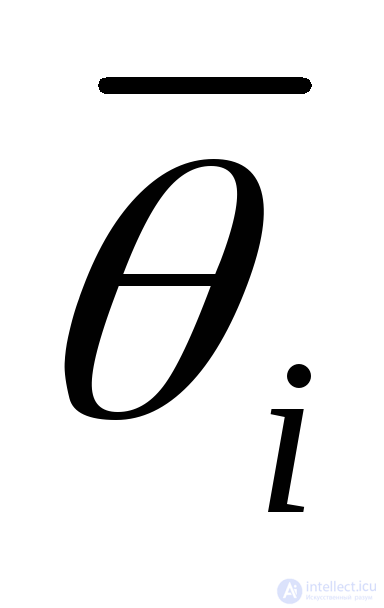могут быть определены при заданных показателях безотказности и ремонтопригодности по всемlсн.пр.видам отказов. Если обозначить математическое ожидание числа отказовi-го вида в течение года через, то:

(5.26)

Потеря годовой производительности в связи с отказами:

(5.27)

или с учетом формулы (5.25):

(5.28)

В частном случае, когда в каждом из lсн.пр. отказовых состояний объекта удельная производительность снижается до нуля (Vi=0 для всехi>0), из последнего выражения получаем:

(5.29)

Наконец, при lсн.пр.=1

(5.30)

Рассмотрим теперь себестоимость годового выпуска продукции. При идеальной (абсолютной) надежности объекта все составляющие себестоимости удобно объединить в пять групп:

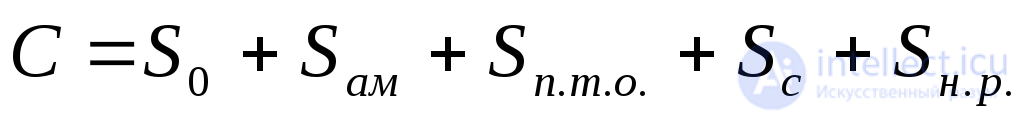(5.31)

где S0– переменная часть себестоимости (стоимость комплектующих материалов, изделий, электроэнергии, рабочей силы и др., непосредственно вошедшая в стоимость произведенной продукции);Sам– годовые амортизационные отчисления на покрытие капитальных вложений;Sп.т.о–стоимость планового технического обслуживания объекта в течение года;Sс– прочие слагающие условно-постоянной части себестоимости (в тм числе общецеховые расходы, расходы на улучшение условий функционирования объекта, содержание и эксплуатацию специального оборудования и др.);Sн.р.– накладные расходы.

Введя обозначения:

(5.32)

перепишем формулу (5.31) в виде:

(5.33)

Если учесть реальную (неабсолютную) надежность объекта, возникают еще три составляющие себестоимос­ти — убытки от брака при отказах (Rбр), затраты на вне­плановые ремонты (Rрем) и убытки при простоях оборудо­вания (Rпр). Об этом говорит сайт https://intellect.icu . Кроме того, в связи с тем, что отказы снижают годовую производительность, возникает “экономия” пере­менной части себестоимости на величинуSсн.пр.. С учетом этого можно записать:

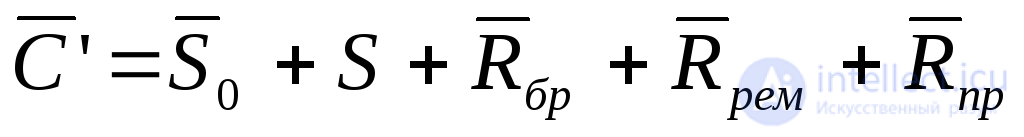(5.34)

где:

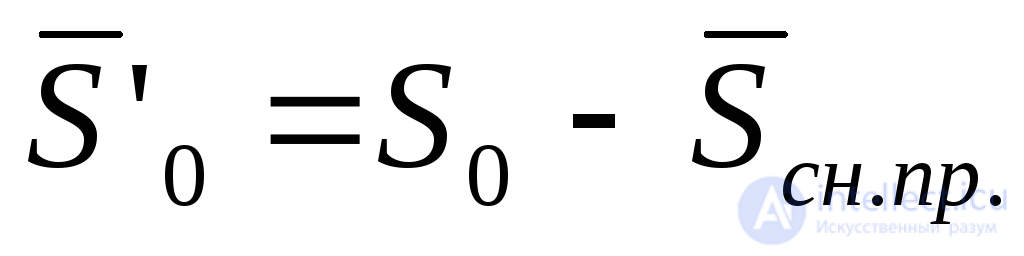(5.35)

Величины Sам,Sп.т.о,S0иSн.рне зависят от числа отка­зов объекта в текущем году и являются детерминированными.

Из формул (5.34) и (5.23) следует, что все показатели эко­номической эффективности, определяемые через Ц'иС', также следует рассматривать как математические ожидания соответствующих случайных величин.

Если обозначить переменную часть себестоимости еди­ницы выпускаемой продукции через S0,0 , можно записать:

(5.36)

Рассмотрим теперь выражение для годовой прибыли с учетом надежности. На основе равенства (5.2) с учетом фор­мул (5.23) и (5.34), произведя несложные преобразования, получим:

(5.37)

где:

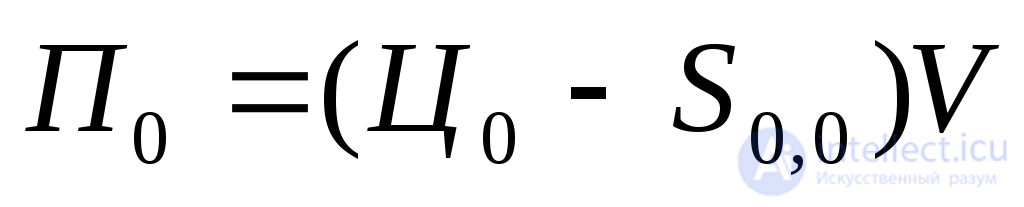(5.38)

(5.39)

(5.40)

Величину П0можно рассматривать как годовую при­быль от некоторого гипотетического идеального объекта - объекта, который при заданной производительности имеет нулевую стоимость, не требует расходов на эксплуатацию и является абсолютно надежным. При заданных характерис­тиках реального объекта расчетП0не представляет затруд­нений. Очень важно, что величинаП0не является функцией надежности объекта: она детерминирована и зависит толь­ко от таких характеристик объекта и выпускаемого изде­лия, как удельная производительность (быстродействие), цена единицы выпускаемой продукции, трудо- и энерго­емкость изделия и др. Поэтому для различных вариантов объекта, имеющих одни и те же производственные характе­ристики и различающихся только уровнем надежности, ве­личинаП0остается одной и той же. При этом любые меро­приятия, направленные на повышение надежности, не ока­зывают влияния наП0.

Выясним физический смысл введенных выше величин S и . Надежность функционирования любого объекта обеспечивается, с одной стороны, затратами в процессе его разработки и изготовления, а с другой — условиями эксплуа­тации и качеством и интенсивностью его технического об­служивания, что в конечном счете также связано с опре­деленными затратами. В связи с этим каждую из состав­ляющих величины S в формуле (5.32) можно рассматривать как составляющую затрат, обеспечивающих достигнутый уровень эксплуатационной надежности объекта. Это поз­воляет назвать величину S, которая связана с уровнем эксплуатационной надежности прямой монотонной зависи­мостью, стоимостью надежности объекта. Нетрудно ви­деть, что стоимость надежности S является величиной де­терминированной, не зависящей от числа отказов объекта в текущем году.

Выше уже отмечалось, что каждая из слагающих в вы­ражении (5.39) является случайной величиной, значение ко­торой для данного года зависит от числа имевших место от­казов объекта. С ростом числа отказов величина этих со­ставляющих возрастает. Если рассмотреть математические ожидания этих величин (,,,), то ясно, что они являются монотонно-убывающими функциями на­дежности объекта. В связи с этим величинуудобно на­зватьценой ненадежностиобъекта (в данных конкретных условиях его применения).

Слагаемые цены ненадежности 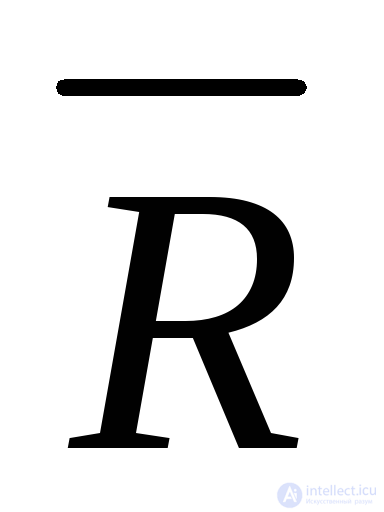необходимо вычислять с учетом всех видов отказов, свойственных рассматри­ваемому объекту, причем по каждому виду отказов должны отдельно задаваться показатели надежности (безотказность и ремонтопригодность) и вычисляться потери. В соответ­ствии с этим для вычисления составляющих,и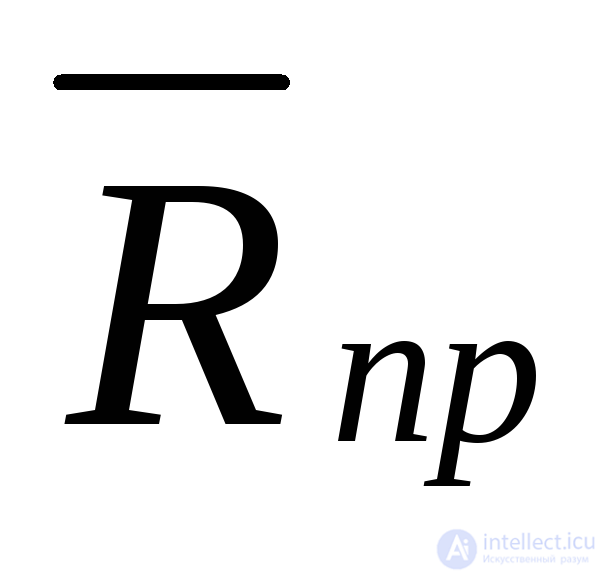 должны использоваться формулы:

; (5.41)

; (5.42)

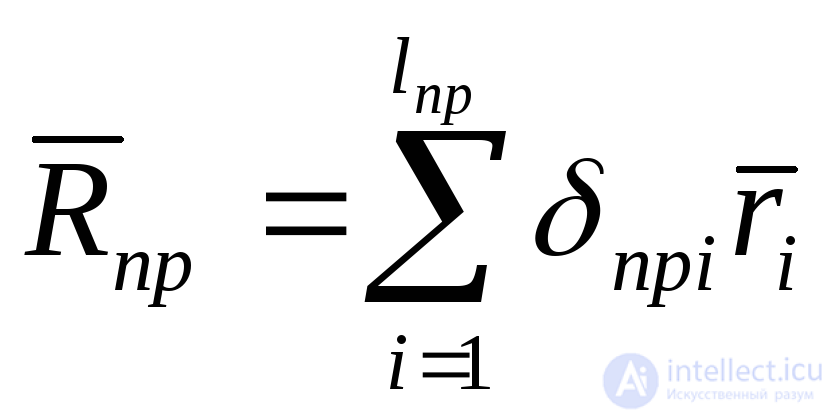(5.43)

где i— среднее значение убытков по соответствующей со­ставляющейпри одном отказе i-го вида *.

Входящие в формулы (5.41) — (5.43) величины рас­считывают по известным в теории надежности формулам на основании данных о надежности объекта по конкретному виду отказов; величины,иопределяют путем сбора соответствующих статистических данных.

Составляющую цены ненадежности можно опре­делить по формуле (5.40). Кроме того, на основе выражений (5.40) и (5.28) имеем

.

Если ввести понятие среднего значения потерь от сниже­ния производительности при одном отказе i-го вида, обо­значив его через

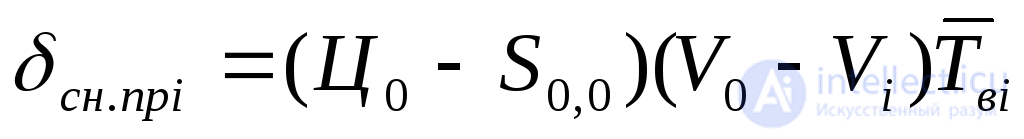, (5.44) выражение длялегко привести к стандартной форме:

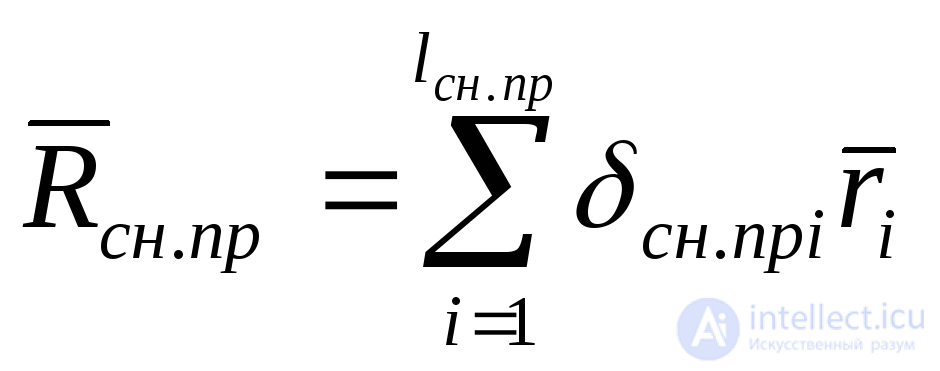, (5.45)

* В общем случае, очевидно, величины lбр,lрем , lпри lсн.пр могут быть неравными, поскольку какие-либо два вида отказов могут оказы­вать одинаковое влияние на одну составляющуюRи совершенно раз­личное на другую.

Величины сн.прi для вычисления по формуле (5.45) иногда можно определить непосредственно путем сбора со­ответствующих статистических данных или анализа функ­ционирования объекта, без фиксации промежуточных па­раметровЦ0,V0, Vi.

Следует подчеркнуть две особенности введенных выше экономических показателей Sи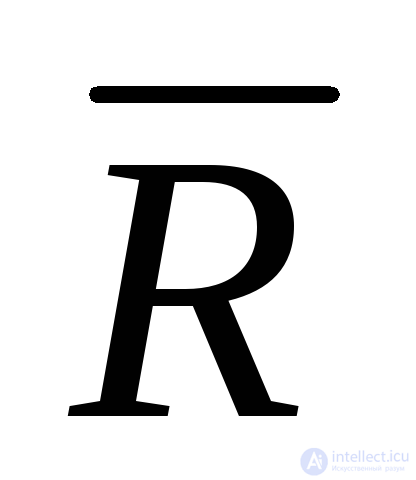. ВеличинаSхарактери­зует прежде всего сам рассматриваемый объект и не связа­на с конкретными условиями его применения. Величина жетеснейшим образом связана именно с конкретными усло­виями применения объекта, включая такие факторы, как цена единицы выпускаемой продукции, переменная часть себестоимости, стоимость исходных материалов и комплек­тующих, наличие защиты от аварий, организация техниче­ского обслуживания и т. п.

Полученные выше формулы для ,ипозволяют записать выражения для расчета показателей экономиче­ской эффективности с учетом надежности. Подставив выра­жение (5.37) в формулу (5.1), получим для математическою ожидания коэффициента экономической эффективности

. (5.46)

Выражение (5.46) очень просто и удобно для анализа ро­ли отдельных составляющих в формировании значения ис­комого коэффициента Эк.п. Так, например, если малоП0, то это означает, что экономически невыгодно технологическое применение объекта или неверно установлена цена еди­ницы выпускаемой продукции, и никакие поиски оптималь­ных требований к надежности не могут существенно улуч­шить положение. Если же, например, относительно велика составляющая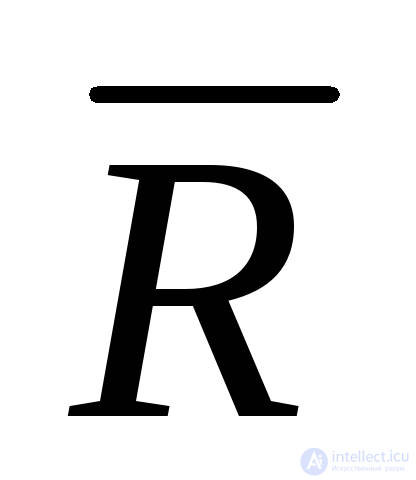(по сравнению с S), то из этого следует, чтоЭк.пможет быть улучшен

применением тех или иных методов повышения надежности функционирования объекта. . Наконец, если относительно велика составляющая S, то, повысить эффективность можно путем снижения стоимости объекта, даже ценой снижения его надежности. Выражение (5.46), кроме того, удобно в тех случаях, когда имеется рас­считанное значениеЭк.пв предположении абсолютной на­дежности объекта и необходимо лишь дополнительно учесть его реальную надежность. Это означает, что известныП = П0- S иК. Остается рассчитать лишьи учесть его в соответствии с формулой (5.46).

С учетом формулы (5.34) на основе выражения (5.7) мож­но записать следующее выражение для математического ожидания приведенных затрат на единицу выпускаемой продукции:

. (5.47)

Нетрудно видеть, что лишь составляющие ,,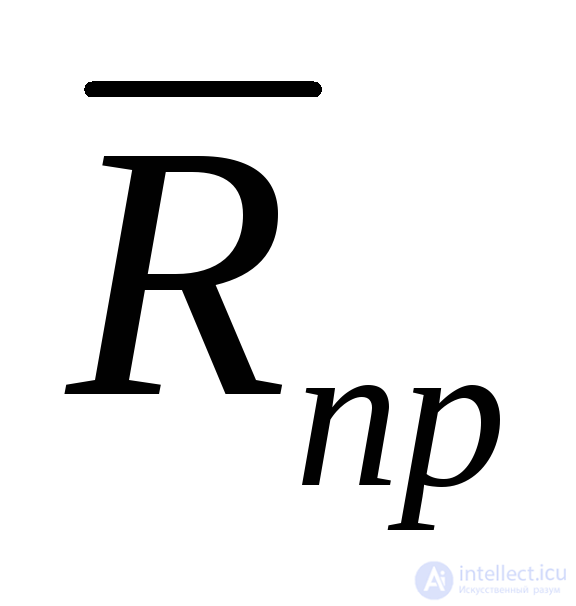и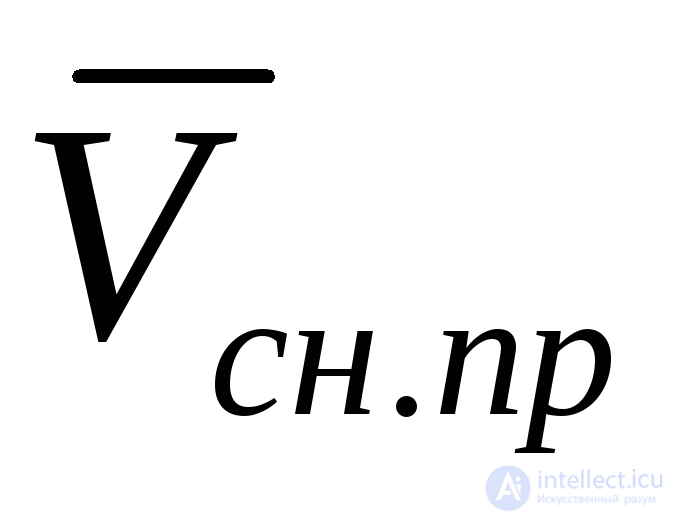отличают последнее выражение от выражения для удельных приведенных затрат, вычисляемых без учета надежности. Как и в случае вычисленияЭк.п, это позволяет без особого труда произвести дополнительный учет надеж­ности в расчете приведенных затрат, если этот показатель ранее уже был вычислен в предположении абсолютной на­дежности рассматриваемого объекта.

Приведем пример использования полученных выше фор­мул для расчета показателей экономической эффективности промышленных объектов с учетом надежности.

Пример 2. Пусть спроектирован некоторый промышленный объ­ект, для которого определены следующие основные показатели:

V=30000 шт.; Ц0=1,5 руб.; Ц=45000 руб.; С=36000 руб.;

К=65000 руб.;  =8000 ч; V0=3,75 штук/ч; S0,0=0,6 руб.

И рассчитаны показатели экономической эффективности без учета надеж­ности (точнее, в предположении абсолютной надежности, когда объект работает без отказов):

; руб.

Пусть у объекта имеются три вида отказов, существенно различаю­щиеся как характеристиками и показателями надежности, так и вызывае­мыми последствиями. Пусть определены (путем расчетов или сбора стати­стических данных) следующие показатели безотказности и ремонто­пригодности для всех трех видов отказов:

и следующие показатели потерь и убытков:

бр1=5 руб., рем1=1 руб., пр1=0, V1=0,

бр2=0, рем2=1 руб., пр2=0, V2=0,

бр3=8 руб., рем3=30 руб., пр3=0, V3=0,

(последние две колонки в этих формулах означают, что для всех тpexвидов отказов отсутствуют убытки, связанные с простоем оборудования при отказах, и что при каждом отказе удельная производительность объекта падает до нуля).

Вычислим необходимые технические и экономические показатели, связанные с отказами объекта и используемые при расчете показателей экономической эффективности. Среднее число отказов i-го вида в те­чение года вычисляется по формуле

:

;

;

.

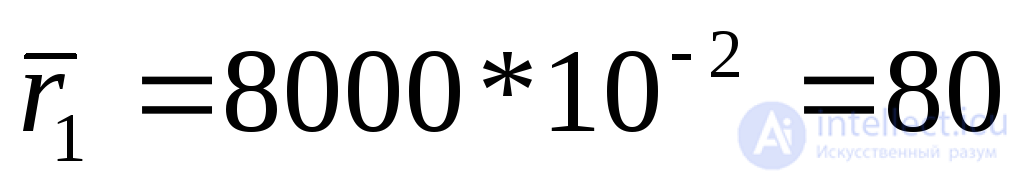По формуле (5.29)

шт.

В соответствии с формулой (5.40) определяем

руб.,

а по формулам (5.41) – (5.43) находим

руб.,

руб.,

.

Далее, в соответствии с формулой (5.39) определяем:

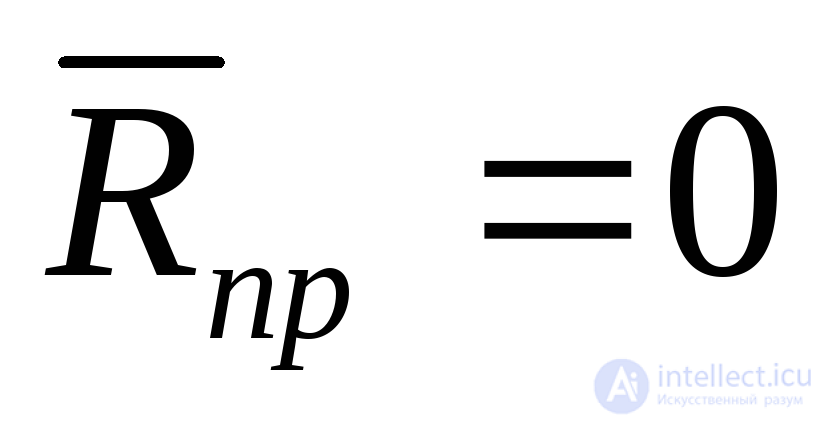R=1485 + 464 + 480 + 0 = 2429 руб.

Воспользовавшись выражениями (5.33) и (5.36), вычисляем также не­обходимую для расчетавеличину S:

S = C – S0,0V = 36000 – 0.6 * 30000 = 18000 руб.

Теперь можно непосредственно определить результирующие пока­затели экономической эффективности объекта (с учетом надежнос­ти). Воспользовавшись формулами (5.46) и (5.47), получаем оконча­тельно:

;

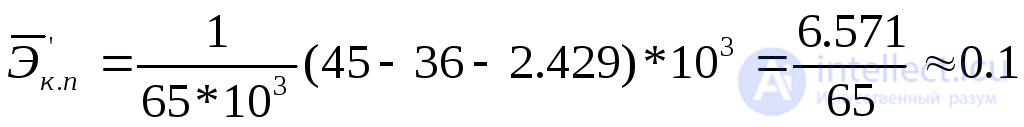руб.

Таким образом, учет реальной надежности объекта в условиях эксплуатации существенно изменил показатели его экономической эф­фективности: Эк.п– с 0,138 до 0,1 иY0– с 1,46 руб. до 1,543 руб.

5.3. Оптимизация надежности по экономическим критериям

Постановка задачи оптимизации надежности предполагает, что в распоряжении разработчика имеется некоторый метод (методы) «управления» надежностью разрабатываемого объекта. Задача состоит в том, чтобы среди уровней надеж­ности объекта, которые могут быть обеспечены в рамках этого метода (методов), найти уровень, отвечающий приня­тому критерию оптимизации.

Методы повышения надежности промышленных объек­тов, можно разбить на четыре группы. В каждой из групп повышение безотказности свя­зано с определенными затратами.* В методах первых двух групп эти затраты производятся один раз — на этапе раз­работки и изготовления — и отражаются в величине капи­тальных вложений Ки, следовательно, составляющейSaxстоимости надежности объекта. Методы третьей группы предполагают затраты на этапе эксплуатации объекта и рассредоточиваются по годам (составляющаяSп.т.о). Нако­нец, методы четвертой группы предусматривают специаль­ные капитальные вложения или специальные текущие затратыSс, которые могут быть сделаны на любом году эксплуатации объекта.

Пусть нас интересует оптимизация некоторого показате­ля надежности объекта а**. Из сказанного выше следует, что при использовании методов любой из четырех групп зависимость S(а); реализуемая за счет любой ее составляю­щей —Sам,Sп.т.оилиSc,— является монотонной и воз­растающей, т. е.

. (5.48)

В то же время повышение надежности объекта снижает потери, связанные с отказами, т. е. цену ненадежности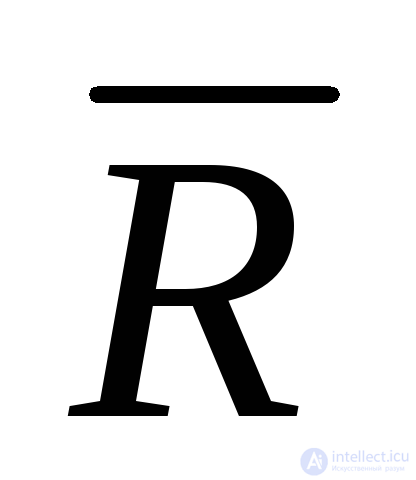

_________

* Мы исключаем из рассмотрения такие счастливые «находки», когда повышение надежности достигается не только без дополнительных затрат, но иногда даже с экономией расходов.

** Поскольку понятие надежности включает в себя четыре составляющие — безотказность, ремонтопригодность, долговечность и сохраняемость, — задача оптимизации может относиться кколичественным показателям любой из этих составляющих, а также к совокупности не­скольких показателей.

_________

по всем ее составляющим. Другими словами,

. (5.49)

Поскольку в выражениях для исоставляющиеSи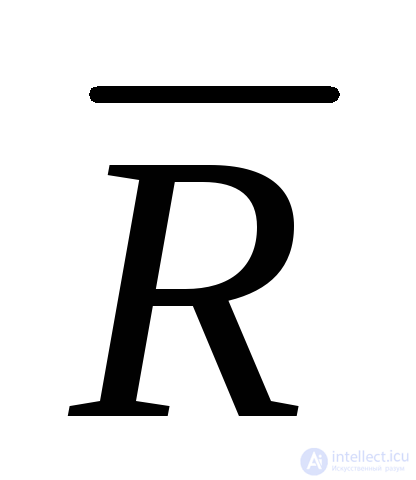суммируются, эти две противоположные тенденции и создают условия для возникновения искомого экстремума показателей экономической эффек­тивности (рис. 6).

(Рис. 6)

Решение задачи оп­тимизации надежности по экономическим кри­териям можно предста­вить следующей после­довательностью этапов:

1) выбор критерия оптимизации (Эк.пmaxилиY0min);

2) выбор оптимизируемого показателя надежности а (группы показателей);

3) определение метода (методов) «управления» надежнос­тью объекта;

4) определение зависимостей К(а) иS(а) [Sам(а),Sп.т.о(а),Sс(а)] для выбранного метода «управления» на­дежностью;

5) определение зависимостей и[,,,] для заданных условий при­менения объекта;

6) исследование выражения 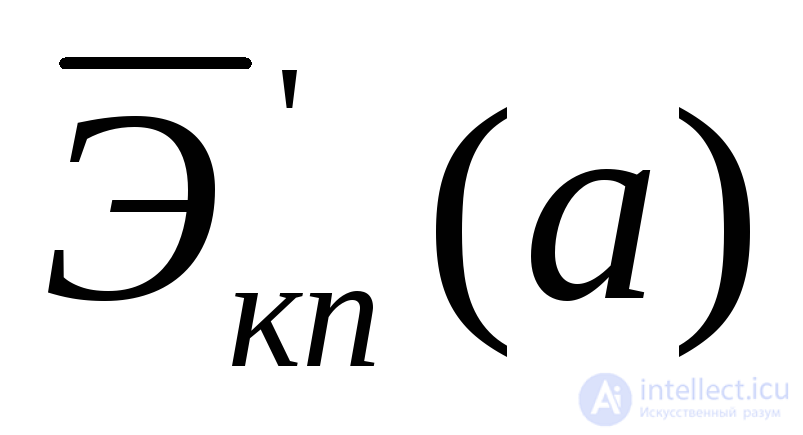на максимум или выраженияна минимум и определениеаopt.

При решении этой задачи возникает трудности тзхнико-экопомического (установление необходимых зависимостей) и чисто математического [определение экстремумов целевой функции или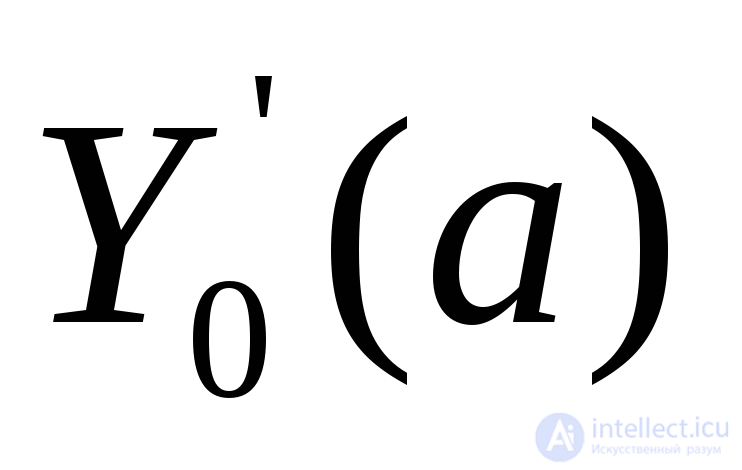] характера.

Прежде всего необходимо отметить, что далеко не всег­да можно найти аналитические зависимости К(а). Наибо­лее широко распространены зависимости вида

,

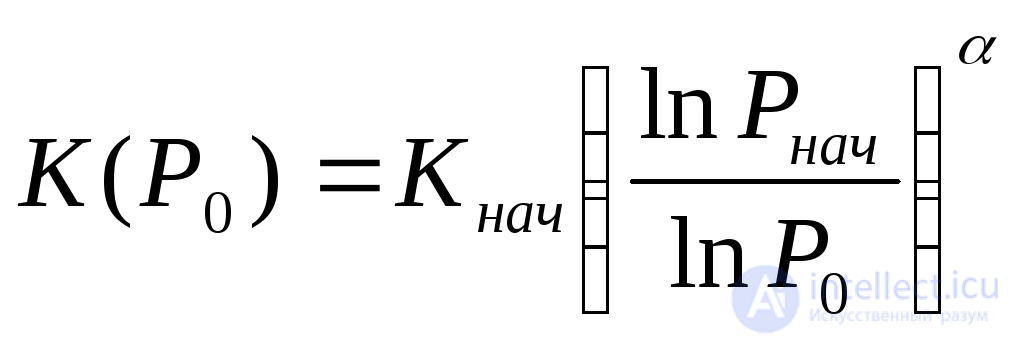где РначиКнач —соответственно вероятность безотказ­ной работы за фиксированное время и стоимость аппарату­ры с некоторым начальным уровнем надежности;= 0,51,5 — коэффициент, зависящий от уровня разра­ботки и производства аппаратуры.

В случае экспоненциального распределения Тзависи­мость (5.50) принимает вид

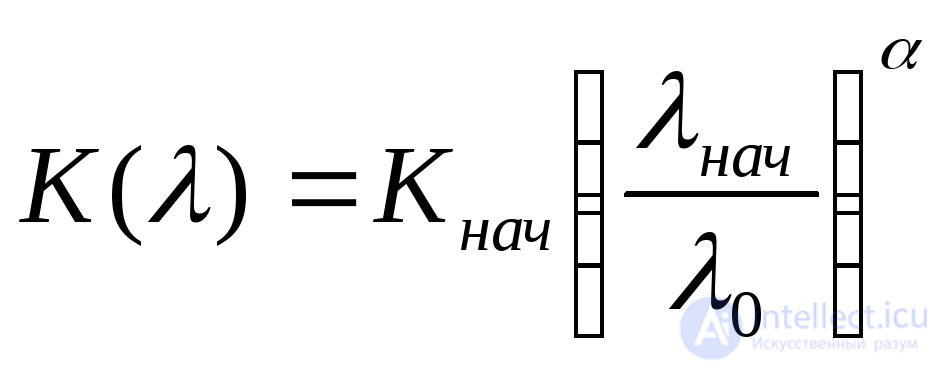. (5.51)

Зависимость (5.50) установлена эмпирически для огра­ниченного круга методов повышения надежности (главным образом, методов конструктивных и технологических), однако, может с успехом использоваться во всех случаях в качестве хотя и приближенной, но достаточно точной моде­ли. Это объясняется тем, что показательная зависимость соответствует характерным чертам реальной связи между стоимостью и надежностью изделии: прямая пропорциональ­ность, монотонность, возрастание крутизны с ростом началь­ного уровня надежности. Небольшое изменение позволяет в широких пределах изменять общую крутизну кривой роста стоимости с надежностью, подгоняя математическую модель (5.50) к любой реальной зависимости.

Несколько проще положение с зависимостям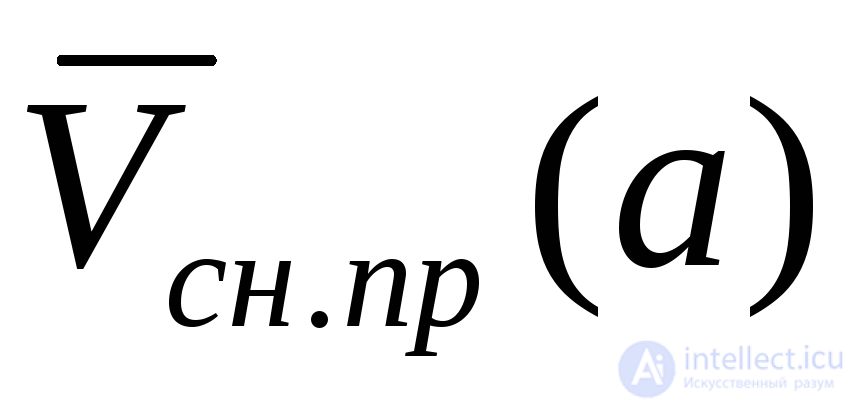и и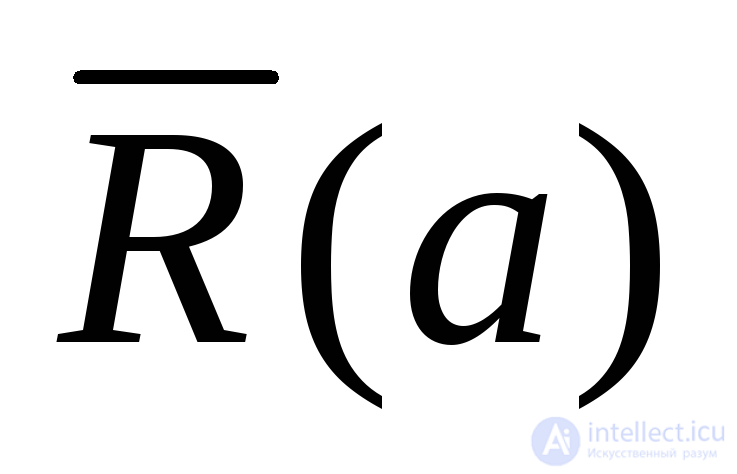, которые определяются через, а расчет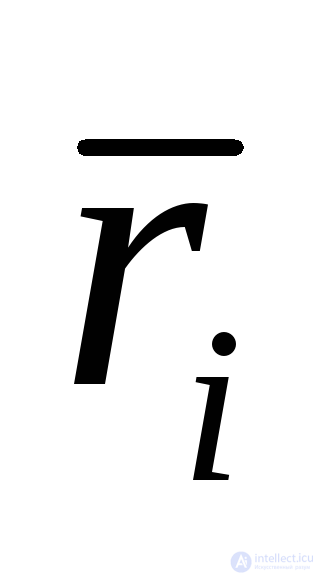при за­данных показателях безотказности и ремонтопригоднос­ти в теории надежности разработан достаточно хорошо.

Остановимся теперь на некоторых особенностях иссле­дования на экстремум выражений и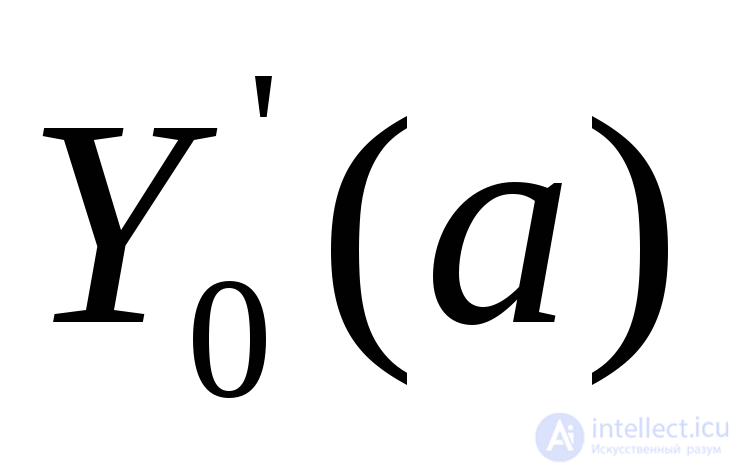. Следует отметить, что во многих случаях выражения дляине являются непрерывными функциями, допускаю­щими дифференцирование и поиск экстремума обычными ме­тодами. Это существенно ограничивает возможности исполь­зования аналитических методов и заставляет обращаться к численным методам, в частности к методам, использующим ЭЦВМ. Очень часто поиск экстремума приходится осуществ­лять путем перебора ряда возможных дискретных значений показателей надежности (возможных вариантов) с расче­том для каждого из них соответствующих показателей эко­номической эффективности и последующего сравнения ре­зультатов. Здесь весьма эффективны методы динамического программирования, позволяющие существенно сократить объем необходимых вычислений.

Функции S(a),,,,и, входящие в выражение для, не включают в себя цены единицы продукцииЦ0,что значительно упрощает получе­ние зависимости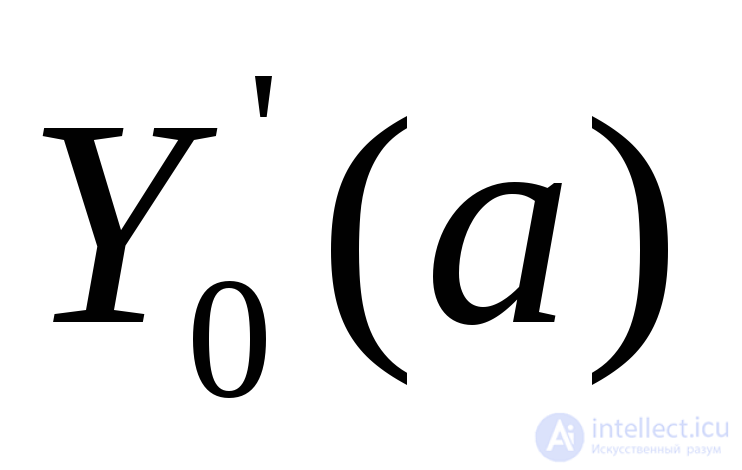и вообще решение задачи оптимиза­ции по критерию (5.14). Существенно сложнее решается задача оптимизации по критерию (5.13). Трудности опреде­ления величиныЦ0во многих случаях вообще не дают воз­можности найти. Кроме того, в некоторых случаях. когдаЦ0известно, нахождение экстремума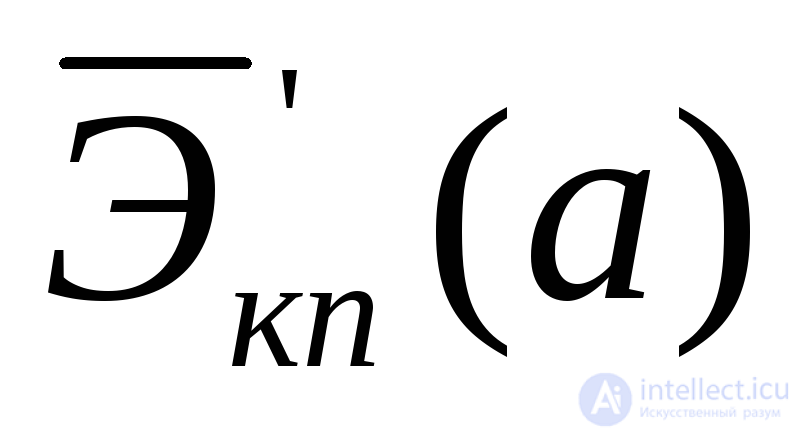сопря­жено и со значительными вычислительными трудностями. В связи с этим иногда приходится отказываться от этого критерия и переходить к другим, более частным, но требую­щим меньше исходной информации или менее громоздких вычислений.

Один из возможных частных критериев — критерий максимума годовой прибыли

(5.52) эквивалентный (ввиду независимости П0 от уровня надеж­ности объекта) критерию минимума суммарных затрат, свя­занных с надежностью:

. (5.53) Очевидно, что исследование на экстремум зависимостисущественно проще, чем зависимости.

Нетрудно видеть, что если используемый метод «управле­ния» надежностью (безотказностью) реализуется на этапе эксплуатации и не затрагивает этапов разработки и изго­товления, К=constи критерии (5.52) и (5.53) совпадают с критерием (5.13). Если жеК=К(а), замена критерия (5.13) критерием (5.53) приводит к неизбежным ошибкам. Поскольку знаменатель выражения (5.3)К(а) является монотонно-возрастающей функцией показателя безотказ­ностиа, можно утверждать, что значениеаopt, определяе­мое по критерию (5.53), находится всегда правее оптимума по критерию (5.13). Другими словами, приближенный опти­мум по критерию (5.53) является верхней границей точного оптимума по критерию (5.13), причем различие между при­ближенным и точным оптимумами тем больше, чем круче возрастаетК(а) с увеличениема.

Цена единицы продукции Ц0входит в формулу для рас­чета составляющейпены ненадежности. Поэтому ясно, что переход к критерию (5.53) не избавляет от необ­ходимости определятьЦ0. В этой связи следует подчерк­нуть, что если величинаЦ0неизвестна, корректное решение задачи оптимизации по критерию (5.13) невозможно. Речь может идти о каких-либо приближенных, ориентировочных решениях, приемлемых лишь для отдельных частных слу­чаев. Так, например, если по характеру и условиям работы объекта можно принять,рас­сматриваемая задача может быть решена без знанияЦ0.

В ряде работ в качестве основного экономического пока­зателя используется величина суммарных потерь от нена­дежности — цена ненадежности ,а в качестве критерия оптимизации — выражение. Должно быть ясно, однако, что использование этого критерия для решения за­дачи оптимизации надежности не имеет смысла, поскольку в этом случаеаopt=amax.

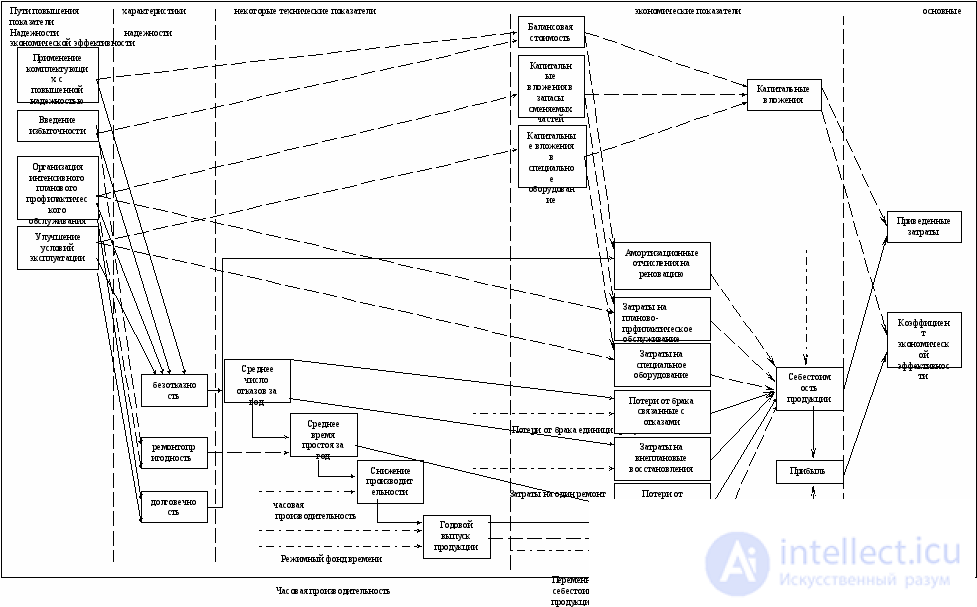
В заключение сделаем следующее дополнение. Рассмот­ренные задачи достаточно сложны. Имеет место сложная цепь влияний методов повышения надежности на показате­ли безотказности, ремонтопригодности и долговечности объекта, этих показателей — на технические и экономиче­ские показатели и, наконец, последних — на показатели экономической эффективности. Четкое представление об этих связях дает схема, изображенная на рис. 7 . На этой схеме сплошные линии отображают положитель­ные влияния, штриховые — отрицательные, а штрих-пунк­тирными линиями изображено введение необходимых для расчетов дополнительных данных.

Приведем пример решения задачи оптимизации надежнос­ти по экономическим критериям.

Пример 3.Пусть имеется некоторый технологический объект со следующими параметрами:

nпроф=12.; Ц0=1,5 руб.;Sc=2000 руб.;Sп.т.о0=200 руб.;Sн.р.=3000руб.;

К=40000 руб.; =8400 ч;V0=4 штук/ч;S0,0=0,6 руб.

где nпроф— количество сеансов профилактического обслуживания в год. Пусть объект имеет два конструктивно самостоятельных блока (блоки I и II), между которыми общая стоимость объекта распределяется следующим образом:

КI=10000 руб.; КII=30000 руб.

Каждый из двух блоков имеет экспоненциальное распределение време­ни безотказной работы со средними значениями и. Ремонтопригодность опре­деляется величинамии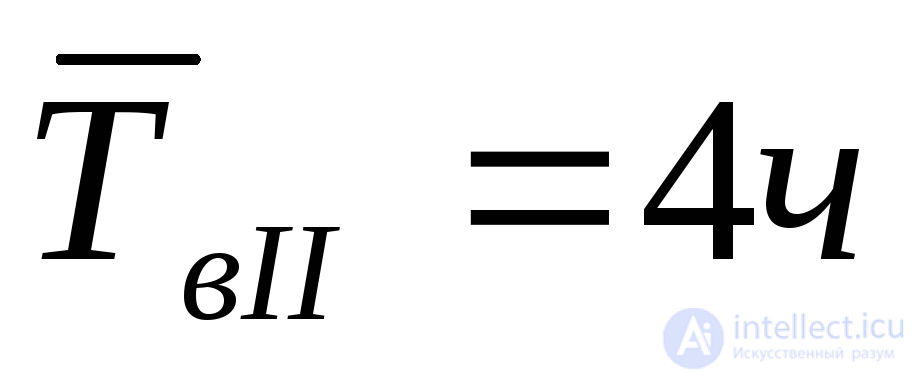, а последствия отказов следующими параметрами:

брI=31 руб.;ремI=13 руб.;прI=11 руб.;

брII=31 руб.;ремII=20 руб.;прII=11 руб.

Любой отказ полностью прекращает функционирование объекта, т. е.

V0I =V0II= 0.

Определим прежде всего показатели экономической эффективнос­ти рассматриваемого объекта. Для этого предварительно рассчитаем по соответствующим формулам ряд промежуточных технических и экономи­ческих показателей:

Теперь в соответствии с формулами (5.46) и (5.47) можно опреде­лить основные показатели экономической эффективности объекта:

Нетрудно видеть из рассчитанных данных, что составляющие цены ненадежностиRу рассматриваемого объекта играют существенную роль в формировании значений показателей его экономической эффек­тивности. В связи с этим представляется возможным улучшить эконо­мические показатели объекта, использовав методы повышения его на­дежности. Возникает задача: найти оптимальный уровень надежности объекта, обеспечивающий максимальную его эффективность.

В качестве критерия оптимизации примем критерий Эк.пmax; оптимизируемым показателем надежности будем считать среднее время безотказной работы обоих блоков объекта.

Пусть в качестве метода «управления» надежностью принято п-кратное «горячее» резервирование. Причем ввиду того, что один из блоков (I) имеет значительно более высокую интенсивность отказов, будет резервироваться только он.

Прежде всего необходимо определить зависимости и. Ввиду того, что принятый метод «управления» надежностью I блока объекта допускает получение лишь дискретного ряда значений (соответствующих целочисленным значениямn), целесообразно просто рассмотреть ряд последовательных вариантов структуры объекта прип=1, 2, З... . При этом стоимостьn-го варианта должна определяться по формуле. Среднее время безотказной работы I блока вi-м варианте, определяется в соответствии с формулой.

Проделаем необходимые расчеты (как было указано в § 5.3, при изменении уровня надежности объекта величина Ц0остается без измене­ний, и необходимо определить лишь изменения в величинахК,SиR):

для п=3:

Таким образом, введение однократного резерва к блоку I (вариант при п= 2) привело к увеличению показателяЭк.пс 1,28 до 1,45. Даль­нейшее углубление резервирования (п= 3) дает уже не увеличение, а снижение этого показателя. Следовательно, оптимальным уровнем на­дежности объекта является уровень, соответствующийп= 2.

Рис.7

5.4. Особенности оценки экономической эффективности и оптимизации надежности технологических комплексов

Автоматизированный технологический комплекс (АТК), включающий технологический объект (ТО) и автоматизи­рованную систему управления (АСУ), может рассматри­ваться как некоторый самостоятельный производственный объект, предназначенный для выпуска определенной про­дукции. Следовательно, решение задач определения эко­номической эффективности и оптимизации для ATК в прин­ципе ничем не отличается от описанного выше решения таких задач для самостоятельных объектов. Есть, однако, и некоторые особенности. Во-первых, если для самостоятель­ного ТО задается один комплект показателей надежности, то для АТК — два таких комплекта (для ТО и АСУ). Во-вто­рых, если для повышения экономической эффективности са­мостоятельного ТО можно управлять только его надеж­ностью, то в случае ТК можно управлять надежностью и ТО, и АСУ. Наконец, в-третьих, при решении задачи опти­мизации в общем случае необходимо найти оптимальное сочетание уровней надежности ТО и АСУ.

Эти особенности и создают необходимость отдельного рассмотрения задачи расчета экономической эффективнос­ти и оптимизации надежности для АТК. При этом в общих формулах для показателей экономической эффективности под капитальными затратами понимается сумма затрат на ТО и АСУ, а в себестоимость выпускаемой продукции вклю­чаются в статьи расходов на эти две составные части АТК (стоимость годового выпуска продукции вычисляется обыч­ным образом).

Условимся обозначать индексами «об» и «с» показате­ли, относящиеся соответственно к ТО и АСУ, а индексом «» — показатели, относящиеся к АТК. Основой для рас­чета остаются выражения (2.46) и (2.47), в кото­рых следует лишь уточнить составляющие.

Под П0следует понимать годовую прибыль от идеаль­ного АТК, в котором и ТО, и АСУ абсолютно надежны и ни­чего не стоят (в производстве и в эксплуатации). ВеличинаSпредставляет собой суммарную стоимость надежности, т. е. приведенную к году сумму затрат на ТО и АСУ:

, (5.54)

или

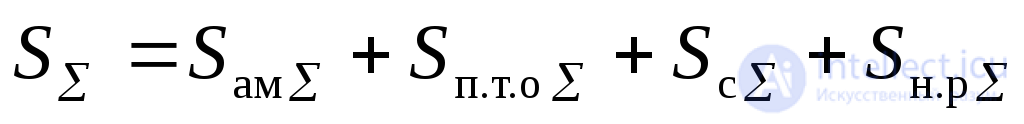. (5.55)

При вычислении следует иметь в виду, что отказы АСУ и ТО могут иметь существенно различные последствия. Соответственно этому можно записать

(5.56) (здесь означает потери от снии-:гния производительности АТК в целом вследствие отказов АСУ, а — то же, вследствие отказов ТО), или

. (5.57)

Вычислять слагаемые в правой части этой формулы можно по формулам (5.41) — (5.43) и (5.45), отвечающим случаю, когда имеются отказы нескольких видов (отказы ТО и АСУ).

С учетом формул (5.55) и (5.57) выражение для годовой прибыли от АТК по аналогии с (5.37) можно записать в виде

(5.58)

Аналогично выражения для с учетом формул (5.55) и (5.57) принимают вид:

где S0,0— переменная часть себестоимости единицы вы­пускаемой АТК продукции;V —годовая производитель­ность АТК при абсолютной надежности ТО и АСУ;— величина снижения годовой производительности за счет отказов ТО и АСУ.

Группировка всех составляющих себестоимости выпуска­емой АТК продукции, предлагаемая в формулах (5.59) и (5.60), позволяет ясно видеть роль различных факторов, связанных с надежностью АСУ и ТО, в формировании зна­чений результирующих показателей экономической эффек­тивности АТК.

Используя принятые выше обозначения, расчетные формулы (5.56) и (5.60) можно переписать в виде:

Формулы (5.61) и (5.62) служат также основой для решения задачи оптимизации надежности АТК. Обозначим обобщенные качественные показатели надежности ТО и АСУ соответственно через аоб и ас. Из анализа выражений (5.61) и (5.60) получаем:

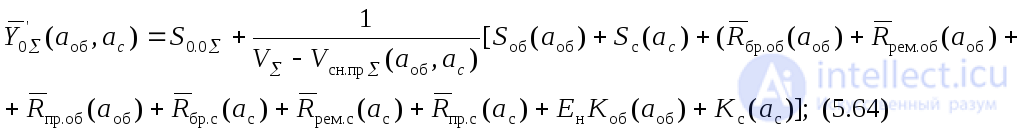
Из постановки задачи и из этих выражений видно, что в наиболее общем случае задачи оптимизации АТК есть задача, по меньшей мере с двумя переменными – аоб и ас . Другими словами, речь идет о нахождении оптимального сочетания уровней надежности АСУ и ТО. Естественно, задача эта сложней, чем для самостоятельного объекта , однако методы ее решения те же.

Вопросы для самоконтроля:

1. В чем заключается основной недостаток существующих методов оценки экономической эффективности АСУ?

2. Какие пути сравнения различных обектов по экономической эффективности Вы знаете? В чем их достоинства и недостатки?

3. Что такое коэффициент прогрессивности технического решения?

4. Как может влиять надежность на экономическую эффективность?

5. Что такое цена ненадежности объекта?

6. Выполните расчет показателей эффективности промышленных объектов с учетом надежности для следующего примера:

Пусть спроектирован некоторый промышленный объект, для которого определены следующие основные показатели:

V= 22000 шт; Ц0=1. 2руб.; Ц=32000 руб.; С=27000 руб.;

К=45000руб; θ=58000 ч..; V0=3.3 шт/ч;S0,0=0.5 руб.

и рассчитаны показатели экономической эффективности без учета надежности:

Эк.п.=0.128; У0=1.36 руб.

Сделать соответствующие выводы.

1. Для чего необходима оптимизация надежности по экономическим критериям?

2. Какие этапы решения задачи оптимизации можно выделить.

3. В чем заключаются особенности оценки экономической эффективности и оптимизации надежности технологических комплексов.

А как ты думаешь, при улучшении экономическая эффективность и надёжность асу, будет лучше нам? Надеюсь, что теперь ты понял что такое экономическая эффективность и надёжность асу и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория надёжности

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.