Лекция
Сразу хочу сказать, что здесь никакой воды про показатели долговечности, и только нужная информация. Для того чтобы лучше понимать что такое показатели долговечности, показатели ремонтопригодности, комплексные показатели надежности , настоятельно рекомендую прочитать все из категории Теория надёжности.
Для восстанавливаемого объекта, средний срок службы представляет собой среднюю календарную продолжительность эксплуатации объекта от ее начала или ее возобновления после ремонта определенного вида до перехода в предельное состояние.
Средний ресурс представляет собой среднюю наработку объекта от начала эксплуатации или ее возобновления после предупредительного ремонта до наступления предельного состояния. В эксплуатации весьма важно так подобрать параметры объекта по мощности, стратегии технического обслуживания и ремонта, режимов работы, чтобы срок службы и срок срабатывания ресурса совпадали. Опыт эксплуатации объектов массового производства (трансформаторов, выключателей, разъединителей, автоматов и т.п.) показывает, что как наработка на отказ, так и наработка между отказами имеют значительный статистический разброс. Аналогичный разброс имеют также ресурс и срок службы. Этот разброс зависит от технологической культуры и дисциплины, а также достигнутого уровня технологии, как изготовления объектов, так и их эксплуатации (использования по назначению, технического обслуживания, ремонта). Разброс наработки до первого отказа, ресурса и срока службы можно уменьшить при увеличении их значения вышеназванными способами.
Поскольку средний и капитальный ремонты позволяют частично или полностью восстановить ресурс, то отсчет наработки при исчислении ресурса возобновляют по окончании такого ремонта, различая в связи с этим доремонтный, межремонтный, послеремонтный и полный (до списания) ресурс. Встречающийся достаточно часто термин "технический ресурс" представляет собой запас возможной наработки объекта. Полный ресурс отсчитывают от начала эксплуатации объекта до его перехода в предельное состояние, соответствующее окончательному прекращению эксплуатации.
Аналогичным образом выделяют и виды срока службы. Соотношение значений ресурса и срока службы зависит от интенсивности использования объекта. Полный срок службы, как правило, включает продолжительность всех видов ремонта, то есть учитывается календарный срок.
Для невосстанавливаемого объекта ресурс представляет собой среднюю продолжительность работы до отказа или до наступления предельного состояния. Практически эта величина совпадает со средней наработкой до отказа Т1.
Используется также такой показатель долговечности, как гамма-процентный ресурс, представляющий наработку, в течение которой объект не достигает предельного состояния с заданной вероятностью (численно равной заданной величине g в процентах).
При количественном описании этого свойства, которое присуще только восстанавливаемому объекту, время восстановления является случайной величиной, зависящей от целого ряда факторов: характера возникшего отказа; приспособленности объекта (устройства, установки и др.) к быстрому обнаружению отказа; квалификации обслуживающего персонала; наличия технических средств; быстроты замены отказавшего элемента в объекте и др. Время восстановления - это время, затраченное на обнаружение, поиск причины отказа и устранения последствий отказа. Опыт показывает, что в сложных электроустановках (системах) 70-90% времени восстановления приходится на поиск отказавшего элемента [2, 15, 16, 17].
Среднее время восстановления - это математическое ожидание времени восстановления работоспособного состояния объекта после отказа . Из определения следует, что
, (2.17)
где n - число восстановлений, равное числу отказов;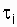 
- время, затраченное на восстановление (обнаружение, поиск причины и устранение отказа), в часах.
Показатель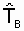 
можно определить и на основании статистических данных, полученных для М однотипных восстанавливаемых объектов. Структура расчетной формулы остается той же:
(2.18)
где М - количество однотипных объектов, для каждого из которых определено общее время восстановления 
за заданное время наблюдений;
, где 
- время восстановления j-го объекта после i-го отказа; nj - количество восстановлений j-го объекта за время наблюдений, причем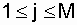 
.
Интенсивность восстановления - это отношение условной плотности вероятности восстановления работоспособного состояния объекта, определенной для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено, к продолжительности этого интервала.
Статистическая оценка этого показателя находится как
, (2.19)
где nв(Dt) - количество восстановлений однотипных объектов за интервал Dt; 
- среднее количество объектов, находящихся в невосстановленном состоянии на интервале Dt.
В частном случае, когда интенсивность восстановления постоянна, то есть m(t) =m= const, вероятность восстановления за заданное время t подчиняется экспоненциальному закону [3, 13, 21] и определяется по выражению
. (2.20)
Этот частный случай имеет наибольшее практическое значение, поскольку реальный закон распределения времени восстановления большинства электроэнергетических объектов (поток восстановлений) близок к экспоненциальному [10, 14]. Используя свойства этого распределения, запишем очень важную зависимость:
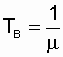, а также 
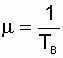. (2.21)
В дальнейшем эта взаимосвязь между Тв и m будет часто использоваться при анализе восстанавливаемых систем.
При более детальных расчетах показателей надежности ремонтируемых (восстанавливаемых) объектов определяется такой показатель ремонтопригодности, как процентное время восстановления g. Это время в течение которого восстановление работоспособности объекта будет осуществлено с вероятностью g , выраженной в процентах .
Процесс функционирования восстанавливаемого объекта можно представить как последовательность чередующихся интервалов работоспособности и восстановления (простоя).
Коэффициент готовности - это вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается . Математическое определение этого показателя дано ниже (разд. 7) при анализе надежности восстанавливаемых систем.
Этот показатель одновременно оценивает свойства работоспособности и ремонтопригодности объекта.
Для одного ремонтируемого объекта коэффициент готовности
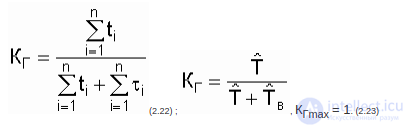
Из выражения 2.23 видно, что коэффициент готовности объекта может быть повышен за счет увеличения наработки на отказ и уменьшения среднего времени восстановления. Для определения коэффициента готовности необходим достаточно длительный календарный срок функционирования объекта.
Зависимость коэффициента готовности от времени восстановления затрудняет оценку надежности объекта, так как по КГ нельзя судить о времени непрерывной работы до отказа. К примеру, для одного и того же численного значения КГ можно иметь малые интервалы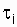 
и ti (см. рис. 2.4) и значительно большие. Таким образом можно доказать, что на конкретном интервале работоспособности вероятность безотказной работы будет больше там, где больше ti, хотя за этим интервалом может последовать длительный интервал простоя 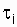. Коэффициент готовности является удобной характеристикой для объектов, которые предназначены для длительного функционирования, а решают поставленную задачу в течение короткого промежутка времени (находятся в ждущем режиме), например, релейная защита, контактная сеть (особенно при относительно малых размерах движения), сложная контрольная аппаратура и т.д.
Коэффициент оперативной готовности КОГопределяется как вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени (кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается) и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.
Из вероятностного определения следует, что
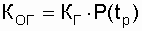, (2.23)
где КГ - коэффициент готовности; Р(tр) - вероятность безотказной работы объекта в течение времени (tр), необходимого для безотказного использования по назначению.
Для часто используемого в расчетной практике простейшего потока отказов, когда
l = w ,Р(tр) соответственно определяется по выражению
.
2.4.3. Коэффициент технического использования
Коэффициент технического использования КТИравен отношению математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации:
где ti - время сохранения работоспособности в i-м цикле функционирования объекта; 
- время восстановления (ремонта) после i-го отказа объекта;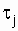 
- длительность выполнения j-й профилактики, требующей вывода объекта из работающего состояния (использования по назначению); n - число рабочих циклов за рассматриваемый период эксплуатации; m - число отказов (восстановлений) за рассматриваемый период; k - число профилактик, требующих отключения объекта в рассматриваемый период.
Как видно из выражения (2.25), коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей (календарной) продолжительности эксплуатации. Следовательно, КТИотличается от КГтем, что при его определении учитывается все время вынужденных простоев, тогда как при определении КГвремя простоя, связанное с проведением профилактических работ, не учитывается.
Суммарное время вынужденного простоя объекта обычно включает время:
В электроэнергетических объектах, к примеру, в трансформаторах, линиях электропередачи, шинах распределительных устройств и т.п., предусмотрены плановые отключения для проведения плановых ремонтов и технического обслуживания. Эти интервалы времени так же как и интервалы, связанные с отключением по причине отказа, учитываются при определении анализируемых коэффициентов надежности.
В условиях эксплуатации на уровень надежности объектов большое влияние оказывают техническое обслуживание и ремонт. Подробно техническое обслуживание и ремонт, стратегии их организации и их решающее влияние на надежность рассматриваются в [1, 16].
ГОСТ 27.002-89 содержит кроме проанализированных в данном пособии наиболее употребляемых показателей надежности и другие показатели: среднюю трудоемкость восстановления, средний срок сохраняемости, гамма-процентный ресурс, гамма-процентное время восстановления, гамма-процентный срок сохраняемости и др. При необходимости определения указанных показателей используются специальные методики, где процедура расчета основывается на тех же законах математической статистики и теории вероятностей, по которым определяются и более широко используемые показатели надежности.
Статью про показатели долговечности я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое показатели долговечности, показатели ремонтопригодности, комплексные показатели надежности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория надёжности
Комментарии
Оставить комментарий
Теория надёжности
Термины: Теория надёжности