4. Надежность невосстанавливаемой системы при основном соединении элементов

Сразу хочу сказать, что здесь никакой воды про надежность невосстанавливаемой системы при основном соединении элементов , и только нужная информация. Для того чтобы лучше понимать что такое надежность невосстанавливаемой системы при основном соединении элементов , настоятельно рекомендую прочитать все из категории Теория надёжности.

4. надежность невосстанавливаемой системы при основном соединении элементов

4.1. Определение вероятности безотказной работы и средней наработки до отказа

Большинство систем спроектировано таким образом, что при отказе любого из элементов система отказывает. При анализе надежности такой системы предполагаем, что отказ любого из элементов носит случайный и независимый характер и не вызывает изменения характеристик (не нарушает работоспособности) остальных элементов. С точки зрения теории надежности в системе, где отказ любого из элементов приводит к отказу системы, элементы включены по основной схеме или последовательно. В понятии отказа заложен физический аналог электрической схемы с последовательным включением элементов, когда отказ любого из элементов связан с разрывом цепи. Но очень часто при расчетах надежности приходится физическое параллельное включение элементов рассматривать как последовательное включение расчетных элементов. Например, некоторый потребитель потребляет электроэнергию по двум одинаковым кабелям, причем сечение жил одного кабеля не в состоянии пропустить всю электрическую нагрузку потребителя. При выходе из строя одного кабеля, оставшийся в работе попадает под недопустимую перегрузку, и этот кабель с помощью защиты отключается - система электроснабжения отказывает, то есть отказ одного из кабелей вызывает отказ электроснабжения. Следовательно, при расчете надежности кабели, как расчетные элементы, имеют последовательную основную схему включения.

Предположим что система состоит из n последовательно включенных элементов. Из теории вероятностей известно, что если определены вероятности появления нескольких независимых случайных событий, то совпадение этих событий определяется как произведение вероятностей их появлений [4, 11, 13]. В нашем случае работоспособное состояние любого из n элементов системы оценивается как вероятность безотказной работы элемента. Система будет находиться в работоспособном состоянии только при условии совпадения работоспособных состояний всех элементов. Таким образом, работоспособность системы оценивается как произведение вероятностей безотказной работы элементов:

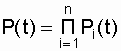, (4.1)

где - вероятность безотказной работы i-го элемента.

Система, как и элемент, может находиться в одном из двух несовместимых состояний: отказа или работоспособности. Об этом говорит сайт https://intellect.icu . Следовательно,

,,

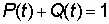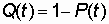где Q(t) - вероятность отказа системы, определяемая по выражению:

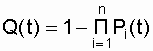. (4.2)

При произвольном законе распределения времени наработки до отказа для каждого из элементов:

, (4.3)

где - интенсивность отказов i-го элемента.

Вероятность безотказной работы системы соответственно запишется:

. (4.4)

По выражению (4.4) можно определить вероятность безотказной работы системы до первого отказа при любом законе изменения интенсивности отказов каждого из n элементов во времени.

Для наиболее часто применяемого условия 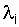= const выражение (4.4) примет вид:

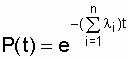, (4.5)

где 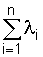можно представить как интенсивность отказов системы, сведенной к эквивалентному элементу с интенсивностью отказов:

= const.

Таким образом, систему из n последовательно включенных элементов легко заменить эквивалентным элементом, который имеет экспоненциальный закон распределения вероятности безотказной работы. А это значит, если l_o= const, то средняя наработка до 
отказа системы 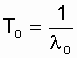. Верно также и то, что при условии: 
l _o= const, искомая величина определится как .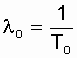

В случае l№const средняя наработка до отказа системы определяется по выражению:

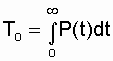, (4.6)

где P(t) находится по выражению (4.4).

4.2. Пример расчета надежности системы, собранной по основной схеме

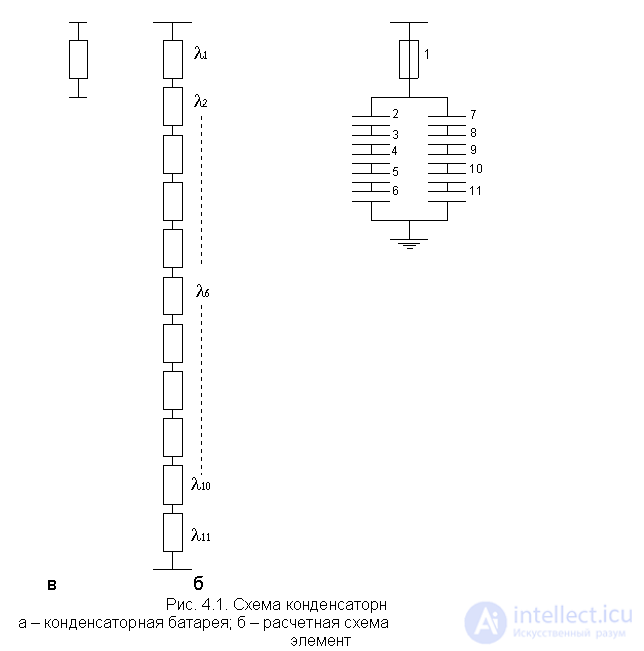
На рис. 4.1,а представлена схема включения конденсаторной батареи (l₂ = l₃ = ... l₁₁ = 0,01 1/год, 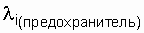= 0,024 1/год). Конденсаторы выбраны так, что при выходе из строя любого из них батарея не выполняет своих функций, то есть с точки зрения надежности она отказывает.

Отказывает она также при перегорании предохранителя 1. Следовательно, мы сформулировали понятие отказа - при отказе любого из элементов система, состоящая из 11 элементов, отказывает. На рис. 4.1,б изображена расчетная схема надежности, где все элементы включены последовательно.

Интенсивность отказов конденсаторной батареи составит:

.

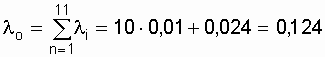На рис. 4.1,в батарея представлена эквивалентным элементом с интенсивностью отказов l_o. По отношению к более сложной системе (схеме), в которой составной частью является конденсаторная батарея, эта установка будет элементом с параметром l_o.

Вероятность безотказной работы батареи за год равна:

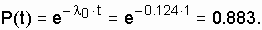
Средняя наработка до отказа равна:

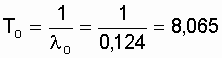года.

Результат расчета доказывает, что надежность неремонтируемой батареи конденсаторов, за 1 год непрерывной работы, мала. Для обеспечения более высокого уровня ее надежности необходимо предусмотреть более качественное техническое обслуживание. Эффект от технического обслуживания подробно рассмотрен в [1, 9].

Статью про надежность невосстанавливаемой системы при основном соединении элементов я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое надежность невосстанавливаемой системы при основном соединении элементов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория надёжности

Из статьи мы узнали кратко, но содержательно про надежность невосстанавливаемой системы при основном соединении элементов