Лекция
Привет, Вы узнаете о том , что такое параллельное соединение, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое параллельное соединение, параллельное соединение в цепях постоянного тока, параллельное соединение в цепях переменного тока , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
Параллельным соединением участков электрической цепи называют соединение, при котором все участки цепи присоединяются к одной паре узлов, т. е. находятся под действием одного и того же напряжения (рис. 3.8). Токи параллельно включенных участков обратно пропорциональны сопротивлениям этих участков.
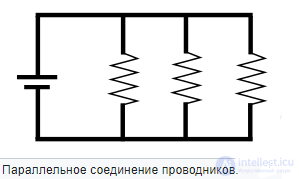
Сила тока в неразветвленной части цепи равна сумме сил тока в отдельных параллельно соединенных проводниках:
Напряжение на участках цепи АВ и на концах всех параллельно соединенных проводников одно и то же:
При параллельном соединении резисторов складываются величины, обратно пропорциональные сопротивлению (то есть общая проводимость складывается из проводимостей каждого резистора
)
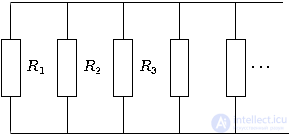
Если цепь можно разбить на вложенные подблоки, последовательно или параллельно включенные между собой, то сначала считают сопротивление каждого подблока, потом заменяют каждый подблок его эквивалентным сопротивлением, таким образом находится общее (искомое) сопротивление.
Для двух параллельно соединенных резисторов их общее сопротивление равно: .
Если , то общее сопротивление равно:
.
При параллельном соединении резисторов их общее сопротивление будет меньше наименьшего из сопротивлений.


.
Цепь замкнута, когда замкнут хотя бы один из выключателей. (аналог Логическая операция ИЛИ).
При параллельном соединении сопротивлений R1, R2 и R3 токи потребителей соответственно равны
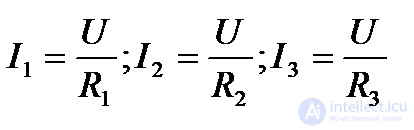
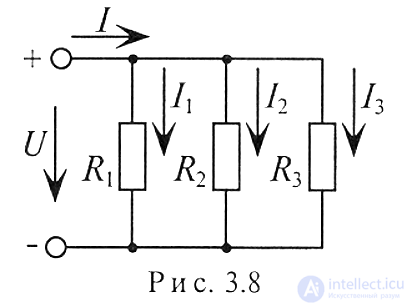
Воспользовавшись первым законом Кирхгофа, можно определить ток I в неразветвленной части цепи
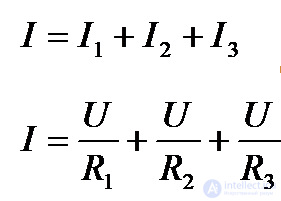
Тогда 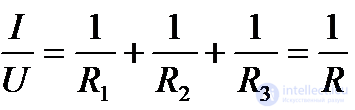 (1.30)
(1.30)
Таким образом, обратная величина общего (эквивалентного) сопротивления R параллельно включенных потребителей равна сумме обратных величин сопротивлений этих потребителей.
Величина, обратная сопротивлению, определяет проводимость потребителя g. Тогда общая (эквивалентная) проводимость цепи при параллельном соединении потребителей определяется суммой проводимостей потребителей
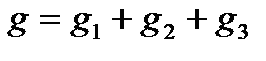 (1.31)
(1.31)
Если параллельно включены n одинаковых потребителей с сопротивлением R/ каждый, то эквивалентное сопротивление этих потребителей 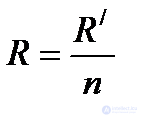 . Если параллельно включены два потребителя с сопротивлениями R1 и R2, то их общее (эквивалентное) сопротивление в соответствии с (1.30) равно
. Если параллельно включены два потребителя с сопротивлениями R1 и R2, то их общее (эквивалентное) сопротивление в соответствии с (1.30) равно
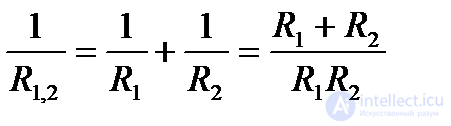
Откуда 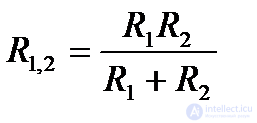 (1.32)
(1.32)
Если параллельно включены три потребителя с сопротивлениями R1, R2, R3, то общее их сопротивление (см. (1.30))
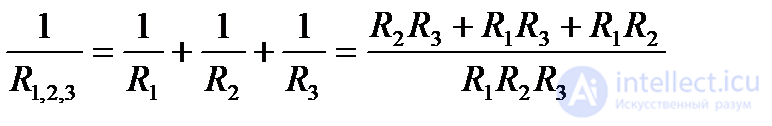
Откуда 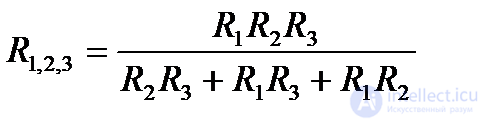 (1.33)
(1.33)
Изменение сопротивления какого-либо из параллельно соединенных потребителей не влияет на режим работы (напряжение) других потребителей, включая изменяемое. Поэтому параллельное единение нашло широкое практическое применение.
При параллельном соединении потребителей на большем сопротивлении тратится меньшая мощность:
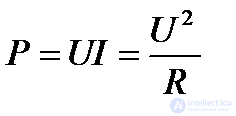
Потенциальная диаграмма
При изучении и расчете некоторых электрических цепей необходимо определить потенциалы отдельных точек цепи и построить потенциальную диаграмму. Для этого можно использовать выражение (3.4) (рис. 3.1а).
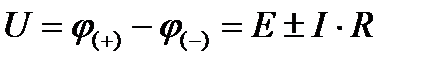
На участке АВ точка В имеет положительный потенциал 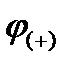 , точка А - отрицательный потенциал
, точка А - отрицательный потенциал 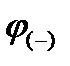 , поэтому
, поэтому 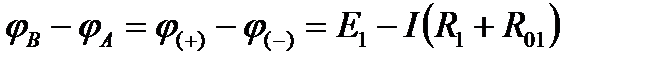 , так как источник работает в режиме генератора, т. Об этом говорит сайт https://intellect.icu . е.
, так как источник работает в режиме генератора, т. Об этом говорит сайт https://intellect.icu . е.
 .
.
На участке ВС точка В имеет положительный потенциал 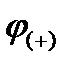 , точка С - отрицательный
, точка С - отрицательный 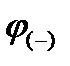 , поэтому
, поэтому 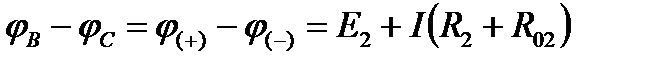 , источник с ЭДС Е2 работает в режиме потребителя, т. е.
, источник с ЭДС Е2 работает в режиме потребителя, т. е.
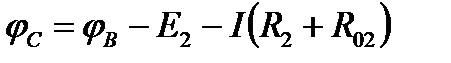 .
.
Таким образом, потенциал точки D можно записать
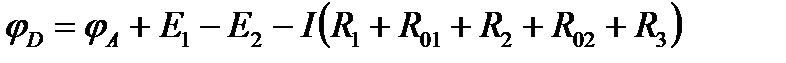 ,
,
если обходить цепь по направлению тока, или
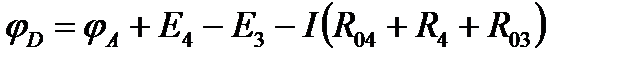 ,
,
если обходить цепь против направления тока.
Отсюда можно сделать следующий вывод (правило): если обходить цепь или участок цепи по направлению тока, то потенциал в каждой точке определяется потенциалом предыдущей точки плюс ЭДС источника, работающего в режиме генератора, минус ЭДС источника, работающего в режиме потребителя, и минус падение напряжения на участке между точками цепи.
При обходе контура против направления тока знаки ЭДС и падения напряжения изменяются на противоположные.
Это правило особенно удобно применять в тех случаях, когда в цепи имеются участки с несколькими источниками.
Потенциальная диаграмма представляет собой график зависимости потенциалов точек цепи от величины сопротивлений участков между этими точками.
Для построения потенциальной диаграммы одну из точек электрической цепи условно заземляют, (потенциал ее принимают равным нулю), а потенциалы остальных точек равны напряжению между ними и заземленной точкой.
Потенциальная диаграмма представляет собой ломаную линию (рис. 3.3).
Пример 3.2
Для цепи, изображенной на рис. 3.2, дано:
Е1 = 8 В; Е2 = 24В; Е3 = 9,5 В; R1 = 0,5 Ом; R2 = 1 Ом; R3 = 1,5 Ом; R01 = 0,15 Ом; R02 = 0,1 Ом; R03 = 0 Ом.
1. Определить величину и направление тока в цепи.
2. Определить потенциал точек В, С, D, Е, G, приняв потенциал точки А равным нулю, 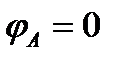 .
.
3. Построить потенциальную диаграмму.
4. Составить и проверить баланс мощностей для цепи.
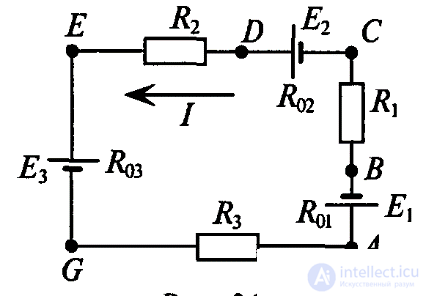
Рис. 3.2.
Решение
1. Выбираем направление обхода контура по часовой стрелке, тогда величина тока
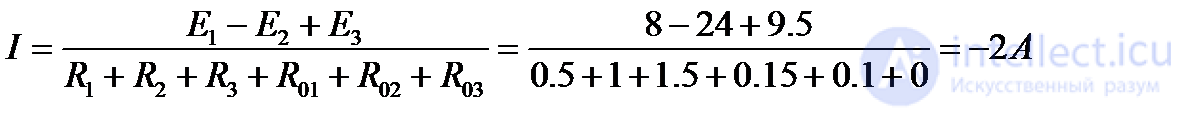
Знак «минус», полученный в результате вычислений, указывает на то, что ток направлен против выбранного направления обхода, как показано на рис. 3.2. В дальнейших расчетах знак «минус» не учитывается. Таким образом, источник ЭДС Е2 работает в режиме генератора, а Е1 и Е3 - потребителей.
2. Для определения потенциалов указанных точек обходим контур по направлению тока. При этом получаем
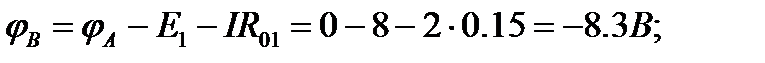
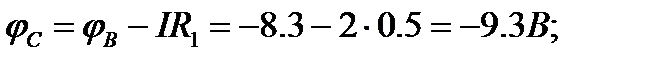
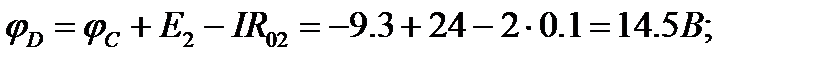
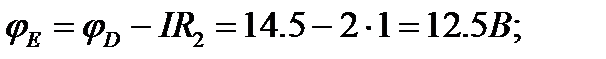
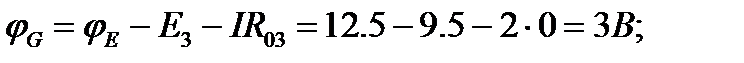
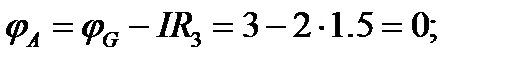
3. Для построения потенциальной диаграммы по оси ординат в масштабе откладываются потенциалы точек, а по оси абсцисс - сопротивления участков. Потенциальная диаграмма изображена на рис. 3.3.
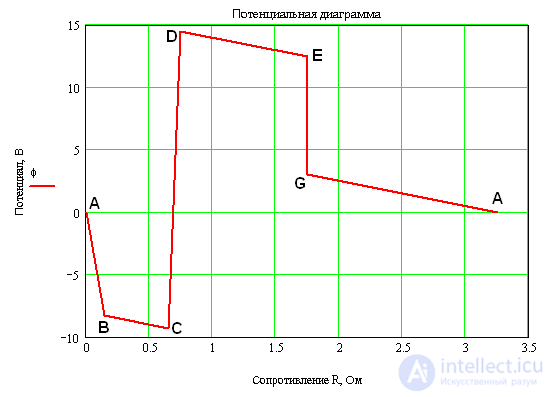
Рис. 3.3
4. Баланс мощностей в электрической цепи с несколькими источниками соблюдается при условии, что сумма мощностей источников, работающих в режиме генераторов, равна сумме мощностей источников, работающих в режиме потребителей, и потерям мощностей на всех сопротивлениях цепи, включая внутренние сопротивления источников:
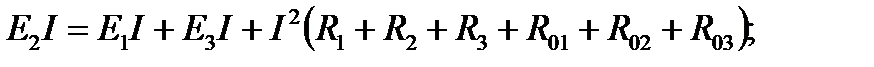
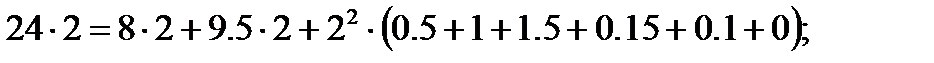
48 Вт = 48 Вт.
Пример 2.
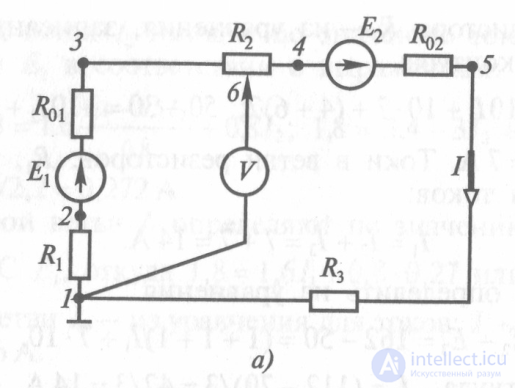
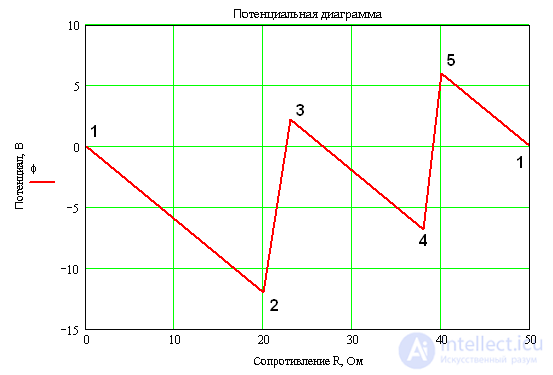
Рассчитать и построить потенциальную диаграмму для электрической цепи постоянного тока (рис. 1.19, а), если дано: ЭДС источников питания Е1 = 16 В; Е2 = 14 В, внутреннее сопротивление R01 = 3 Ом; R02 = 2 Ом, сопротивления резисторов R1 = 20 Ом; R2 = 15 Ом; R3 = 10 Ом. Определить положение движка потенциометра, в котором вольтметр V покажет нуль, составить баланс мощностей для цепи. Как повлияет на вид потенциальной диаграммы выбор другой точки с нулевым потенциалом?
б)
Рис. 1.19.
Решение. Ток в цепи определяют по уравнению, составленному по второму закону Кирхгофа, приведенному к виду:
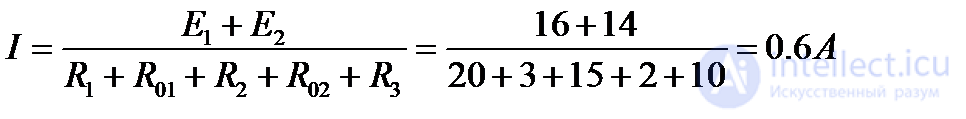
Потенциальную диаграмму строят в прямоугольной системе координат. При этом по оси абсцисс откладывают в соответствующем масштабе сопротивления всех участков цепи, а по оси ординат - потенциалы соответствующих точек. При построении потенциальной диаграммы одна из точек цепи условно заземляется, т. е. принимается, что потенциал ее φ = 0. На диаграмме эта точка помещается в начале координат.
В соответствии с условием задачи определяют потенциалы точек 1 - 5 электрической цепи, при этом принимают потенциал φ1 точки 1 цепи равным нулю.
Потенциал φ2 точки 2 находят из выражения, записанного по второму закону Кирхгофа для участка 1 - 2 цепи:
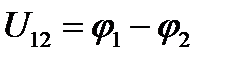
откуда 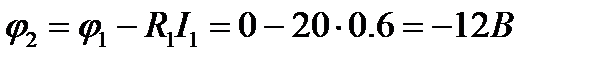 .
.
Координаты точки 2: R = 20 Ом; φ2 = -12 В.
По второму закону Кирхгофа для участка цепи 1 - 3 справедливо уравнение:
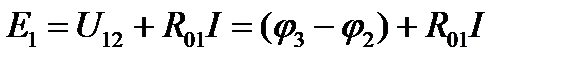 ,
,
откуда потенциал точки 3 цепи: 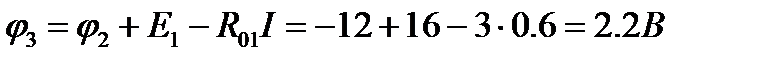 .
.
Координаты точки 3 цепи: R = 20 + 3 = 23 Ом; φ3 = 2,2 В. Аналогично определяют потенциал точки 4 цепи:
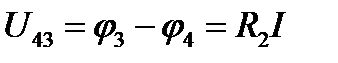 ,
,
откуда 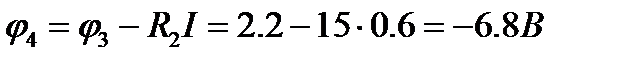 .
.
Координаты точки 4 цепи: R = 23 + 15 = 38 Ом; φ4 = - 6,8В.
Потенциал φ5 точки 5 цепи находят из уравнения, записанного по второму закону Кирхгофа для участка 4 - 5 цепи:
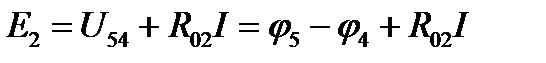 ,
,
откуда 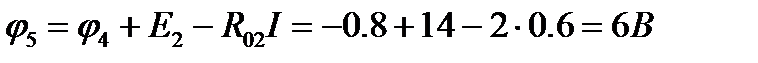 .
.
Координаты точки 5 цепи: R = 38 + 2 = 40 Ом; φ5 = 6 В. Потенциал φ1 точки 1 цепи находят из уравнения, составленного по второму закону Кирхгофа для участка 4 - 5 цепи: 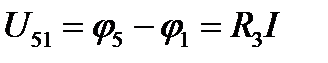 ;
; 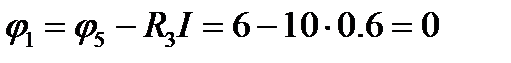 . Координаты точки 1 цепи: R = 40 + 10 = 50 Ом; φ1 = 0.
. Координаты точки 1 цепи: R = 40 + 10 = 50 Ом; φ1 = 0.
Для рассматриваемой электрической цепи по результатам расчетов на рис. 1.19, б приведена потенциальная диаграмма.
Из этой диаграммы следует, что положение движка потенциометра в точке 6 цепи соответствует показанию вольтметра, равному нулю, так как потенциалы точек 1 и 6 цепи равны.
При выборе другой точки электрической цепи с нулевым потенциалом разности потенциалов на соответствующих участках цепи не изменяются, так как они определяются величиной тока и величиной сопротивления. Если принять потенциал точки 3 цепи φ3 = 0, то ось абсцисс переместится в точку 3 потенциальной диаграммы (пунктирная линия), т. е. потенциалы всех точек цепи уменьшаются на величину потенциала φ, равного отрезку 0К = 2,3 В.
Баланс мощностей соответствует следующему уравнению:
 ;
;
16 ∙ 0,6 + 14 ∙ 0,6 = 0,62(20 + 3 + 15 + 2 + 10).
18 Вт = 18 Вт.
Рассмотрим параллельное соединение сопротивлений, когда все ветви электрической цепи (потребители) находятся под одним и тем же напряжением (рис. 2.22).
Для принципиальной схемы параллельного соединения элементов запишем первый закон Кирхгофа в комплексной форме:

Векторы токов в параллельных ветвях:
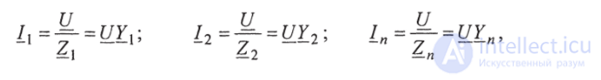
где 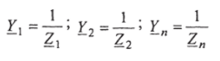 - полные комплексные проводимости 1-й, 2-й, ... n-й ветвей;
- полные комплексные проводимости 1-й, 2-й, ... n-й ветвей;
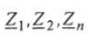 полные комплексные сопротивления 1-й, 2-й, ... n-й ветвей.
полные комплексные сопротивления 1-й, 2-й, ... n-й ветвей.
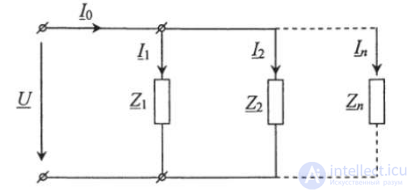
Рис. 2.22. Принципиальная схема параллельного соединения приемников
Общий ток в цепи:
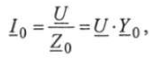
где 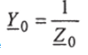 - полная комплексная проводимость параллельного соединения;
- полная комплексная проводимость параллельного соединения;
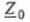 - полное комплексное сопротивление параллельного соединения.
- полное комплексное сопротивление параллельного соединения.
Очевидно, что
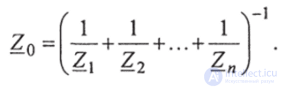
Определим проводимость для 1-й ветви 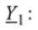
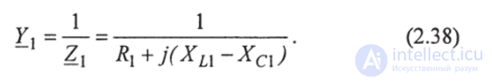
Умножим числитель и знаменатель уравнения (2.38) на 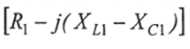 получим:
получим:
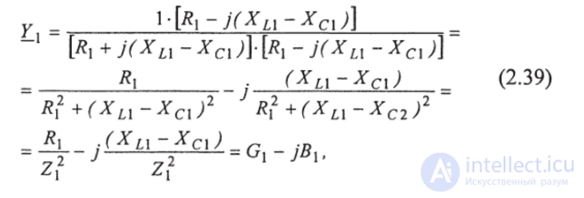
где 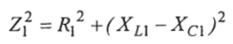 - квадрат модуля полного сопротивления 1-й ветви;
- квадрат модуля полного сопротивления 1-й ветви;
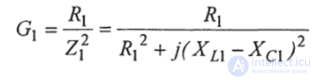 - активная проводимость 1-й ветви;
- активная проводимость 1-й ветви;
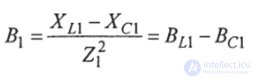 - реактивная проводимость 1-й ветви.
- реактивная проводимость 1-й ветви.
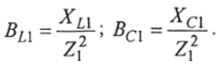
Учитывая соотношения (2.39), полную проводимость для 1-й ветви можно записать в следующем виде:
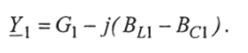
Тогда модуль полной проводимости 1-й ветви

На комплексной плоскости (рис. 2.23) слагаемые комплексной проводимости цепи изображены в виде векторов для двух случаев: ВL1 > Вс1 (рис. 2.23а) и ВL1 < Вс1 (рис. 2.23b). В первом случае комплексная проводимость цепи имеет индуктивный характер, во втором - емкостной.
Если комплексная проводимость цепи имеет индуктивный характер, то общий ток (в неразветвленной части цепи) отстает по фазе от напряжения, так как 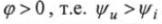 .
.
Если комплексная проводимость цепи имеет емкостной характер, то общий ток опережает по фазе напряжение, так как 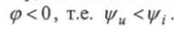 .
.
Заметим, что, как и ранее, положительные значения угла 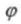 отсчитываются против часовой стрелки от вектора комплексного значения тока
отсчитываются против часовой стрелки от вектора комплексного значения тока 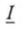 или проводимости
или проводимости 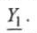
Треугольник проводимости для 1-й ветви представлен на рис.2.23в:
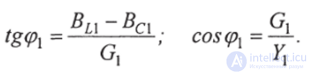
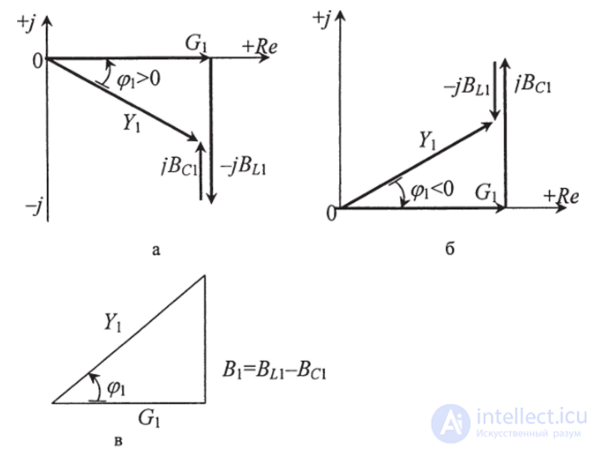
Рис. 2.23. Проводимости для 1-й ветви на комплексной плоскости:
ВL1 > Вс1 (рис. 2.23а)
ВL1 < Вс1 (рис. 2.23b)
треугольник проводимости (в)
Аналогично для всех остальных ветвей находятся проводимости и строятся треугольники проводимости. Следовательно, проводимость для всей цепи
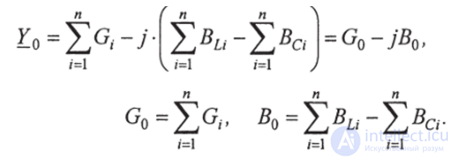
Модуль полной проводимости всей цепи:
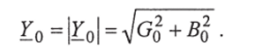
Пример 2.6. В соответствии со схемой (рис. 2.24) дано:
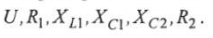
Определить: 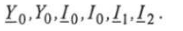
Из треугольника проводимости для параллельной цепи (рис. 2.25)определим угол 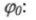
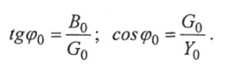
Решение.
1. Находим комплексную проводимость цепи:
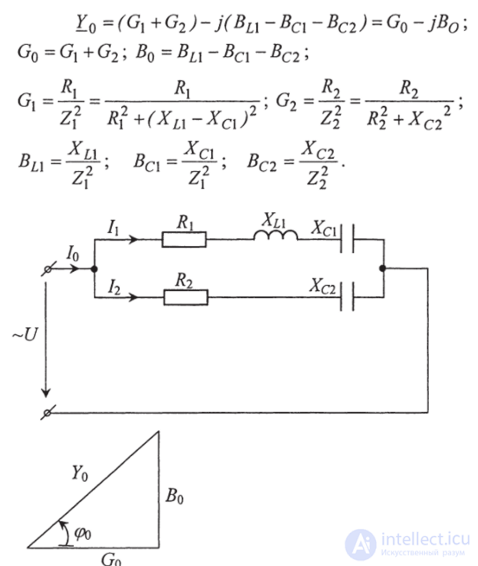
Рис. 2.24. Схема параллельной цепи
Рис. 2.25. Треугольник проводимости параллельной цепи (рис. 2.24)
2. Находим модуль комплексной проводимости цепи:
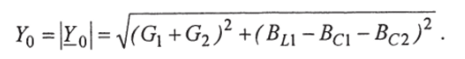
3. Находим комплекс тока, потребляемого цепью от источника энергии: 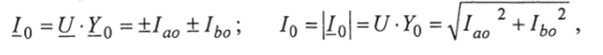
где 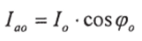 - активная составляющая тока
- активная составляющая тока 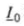 ;
;
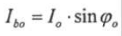 - реактивная составляющая тока
- реактивная составляющая тока 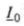 ;
;
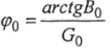 - угол между U0 и /0.
- угол между U0 и /0.
4. Комплексы токов и /2 равны:
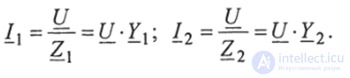
5. По первому закону Кирхгофа ток /0 равен:
Векторную диаграмму для 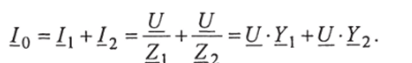
схемы с параллельным соединением элементов, изображенную на рис. 2.26 удобно строить относительно вектора напряжения, так как при данном соединении вектор напряжения является общим для всех
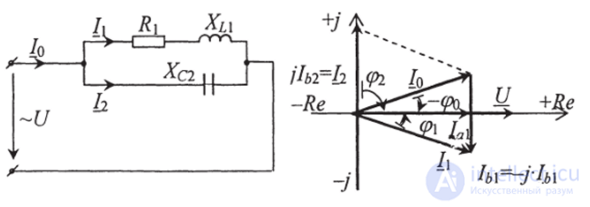
Рис. 2.26. Схема параллельного соединения элементов
Рис. 2.27. Векторная диаграмма при параллельном соединении элементов ветвей. При этом его направляют по вещественной положительной оси (рис. 2.27).
Запишем уравнения для тока и напряжения для схемы рис. 2.26 в комплексном виде:

На векторной диаграмме рис. 2.27 токи в соответствии с уравнениями в ветвях 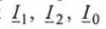 представлены в алгебраической форме записи как сумма активных составляющих токов,
представлены в алгебраической форме записи как сумма активных составляющих токов, 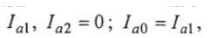 которые находятся как проекции соответствующих векторов токов на ось действительных чисел Rе, и реактивных составляющих токов
которые находятся как проекции соответствующих векторов токов на ось действительных чисел Rе, и реактивных составляющих токов 
 , которые находятся как проекции соответствующих токов на ось мнимых чисел (j).
, которые находятся как проекции соответствующих токов на ось мнимых чисел (j).
Активные и реактивные составляющие токов находятся по формулам:
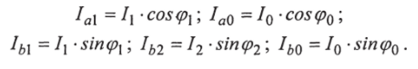
Исследование, описанное в статье про параллельное соединение, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое параллельное соединение, параллельное соединение в цепях постоянного тока, параллельное соединение в цепях переменного тока и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электротехника, Схемотехника, Аналоговые устройства
Комментарии
Оставить комментарий
Электротехника, Схемотехника, Аналоговые устройства
Термины: Электротехника, Схемотехника, Аналоговые устройства