4. Линейные модели классификации и регрессии

Привет, Вы узнаете о том , что такое линейные модели классификации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое линейные модели классификации, линейная регрессия, логическая регрессия, регуляризация логистической регрессии , настоятельно рекомендую прочитать все из категории Машинное обучение.

Машинное обучение

Сегодня мы детально обсудим важный класс моделей машинного обучения – линейных. Ключевое отличие нашей подачи материала от аналогичной в курсах эконометрики и статистики – это акцент на практическом применении линейных моделей в реальных задачах (хотя и математики тоже будет немало).

Пример такой задачи – это соревнование Kaggle Inclass по идентификации пользователя в Интернете по его последовательности переходов по сайтам.

План этой статьи:

1. линейная регрессия
   • Метод наименьших квадратов
   • Метод максимального правдоподобия
   • Разложение ошибки на смещение и разброс (Bias-variance decomposition)
   • Регуляризация линейной регрессии
2. Логистическая регрессия
   • Линейный классификатор
   • Логистическая регрессия как линейный классификатор
   • Принцип максимального правдоподобия и логистическая регрессия
   • L2-регуляризация логистической функции потерь
3. Наглядный пример регуляризации логистической регрессии
4. Где логистическая регрессия хороша и где не очень
   -Анализ отзывов IMDB к фильмам
   -XOR-проблема
5. Кривые валидации и обучения
6. Плюсы и минусы линейных моделей в задачах машинного обучения
7. Домашнее задание №4
8. Полезные ресурсы

1. Линейная регрессия

Метод наименьших квадратов

Рассказ про линейные модели мы начнем с линейной регрессии. В первую очередь, необходимо задать модель зависимости объясняемой переменной от объясняющих ее факторов, функция зависимости будет линейной: . Если мы добавим фиктивную размерность для каждого наблюдения, тогда линейную форму можно переписать чуть более компактно, записав свободный член под сумму: . Если рассматривать матрицу наблюдения-признаки, у которой в строках находятся примеры из набора данных, то нам необходимо добавить единичную колонку слева. Зададим модель следующим образом:

где

• – объясняемая (или целевая) переменная;
• – вектор параметров модели (в машинном обучении эти параметры часто называют весами);
• – матрица наблюдений и признаков размерности строк на столбцов (включая фиктивную единичную колонку слева) с полным рангом по столбцам: ;
• – случайная переменная, соответствующая случайной, непрогнозируемой ошибке модели.

Можем выписать выражение для каждого конкретного наблюдения

Также на модель накладываются следующие ограничения (иначе это будет какая то другая регрессия, но точно не линейная):

• матожидание случайных ошибок равно нулю: ;
• дисперсия случайных ошибок одинакова и конечна, это свойство называется гомоскедастичностью: ;
• случайные ошибки не скоррелированы: .

Оценка весов называется линейной, если

где зависит только от наблюдаемых данных и почти наверняка нелинейно. Так как решением задачи поиска оптимальных весов будет именно линейная оценка, то и модель называется линейной регрессией. Введем еще одно определение. Оценка называется несмещенной тогда, когда матожидание оценки равно реальному, но неизвестному значению оцениваемого параметра:

Один из способов вычислить значения параметров модели является метод наименьших квадратов(МНК), который минимизирует среднеквадратичную ошибку между реальным значением зависимой переменной и прогнозом, выданным моделью:

Для решения данной оптимизационной задачи необходимо вычислить производные по параметрам модели, приравнять их к нулю и решить полученные уравнения относительно (матричное дифференцирование неподготовленному читателю может показаться затруднительным, попробуйте расписать все через суммы, чтобы убедиться в ответе):

Шпаргалка по матричным производным

Итак, имея в виду все определения и условия описанные выше, мы можем утверждать, опираясь на теорему Маркова-Гаусса, что оценка МНК является лучшей оценкой параметров модели, среди всех линейных и несмещенных оценок, то есть обладающей наименьшей дисперсией.

Метод максимального правдоподобия

У читателя вполне резонно могли возникнуть вопросы: например, почему мы минимизируем среднеквадратичную ошибку, а не что-то другое. Ведь можно минимизировать среднее абсолютное значение невязки или еще что-то. Единственное, что произойдет в случае изменения минимизируемого значения, так это то, что мы выйдем из условий теоремы Маркова-Гаусса, и наши оценки перестанут быть лучшими среди линейных и несмещенных.

Давайте перед тем как продолжить, сделаем лирическое отступление, чтобы проиллюстрировать метод максимального правдоподобия на простом примере.

Как-то после школы я заметил, что все помнят формулу этилового спирта. Тогда я решил провести эксперимент: помнят ли люди более простую формулу метилового спирта: . Мы опросили 400 человек и оказалось, что формулу помнят всего 117 человек. Разумно предположить, что вероятность того, что следующий опрошенный знает формулу метилового спирта – . Покажем, что такая интуитивно понятная оценка не просто хороша, а еще и является оценкой максимального правдоподобия.

Разберемся, откуда берется эта оценка, а для этого вспомним определение распределения Бернулли: случайная величина имеет распределение Бернулли, если она принимает всего два значения ( и с вероятностями и соответственно) и имеет следующую функцию распределения вероятности:

Похоже, это распределение – то, что нам нужно, а параметр распределения и есть та оценка вероятности того, что человек знает формулу метилового спирта. Мы проделали независимыхэкспериментов, обозначим их исходы как . Запишем правдоподобие наших данных (наблюдений), то есть вероятность наблюдать 117 реализаций случайной величины и 283 реализации :

Далее будем максимизировать это выражение по , и чаще всего это делают не с правдоподобием , а с его логарифмом (применение монотонного преобразования не изменит решение, но упростит вычисления):

Теперь мы хотим найти такое значение , которое максимизирует правдоподобие, для этого мы возьмем производную по , приравняем к нулю и решим полученное уравнение:

Получается, что наша интуитивная оценка – это и есть оценка максимального правдоподобия. Применим теперь те же рассуждения для задачи линейной регрессии и попробуем выяснить, что лежит за среднеквадратичной ошибкой. Для этого нам придется посмотреть на линейную регрессию с вероятностной точки зрения. Модель, естественно, остается такой же:

но будем теперь считать, что случайные ошибки берутся из центрированного нормального распределения:

Перепишем модель в новом свете:

Так как примеры берутся независимо (ошибки не скоррелированы – одно из условий теоремы Маркова-Гаусса), то полное правдоподобие данных будет выглядеть как произведение функций плотности . Рассмотрим логарифм правдоподобия, что позволит нам перейти от произведения к сумме:

Мы хотим найти гипотезу максимального правдоподобия, т.е. нам нужно максимизировать выражение , а это то же самое, что и максимизация его логарифма. Обратите внимание, что при максимизации функции по какому-то параметру можно выкинуть все члены, не зависящие от этого параметра:

Таким образом, мы увидели, что максимизация правдоподобия данных – это то же самое, что и минимизация среднеквадратичной ошибки (при справедливости указанных выше предположений). Получается, что именно такая функция стоимости является следствием того, что ошибка распределена нормально, а не как-то по-другому.

Разложение ошибки на смещение и разброс (Bias-variance decomposition)

Поговорим немного о свойствах ошибки прогноза линейной регрессии (в принципе эти рассуждения верны для всех алгоритмов машинного обучения). В свете предыдущего пункта мы выяснили, что:

• истинное значение целевой переменной складывается из некоторой детерминированной функции и случайной ошибки : ;
• ошибка распределена нормально с центром в нуле и некоторым разбросом: ;
• истинное значение целевой переменной тоже распределено нормально:
• мы пытаемся приблизить детерминированную, но неизвестную функцию линейной функцией от регрессоров , которая, в свою очередь, является точечной оценкой функции в пространстве функций (точнее, мы ограничили пространство функций параметрическим семейством линейных функций), т.е. случайной переменной, у которой есть среднее значение и дисперсия.

Тогда ошибка в точке раскладывается следующим образом:

Для наглядности опустим обозначение аргумента функций. Рассмотрим каждый член в отдельности, первые два расписываются легко по формуле :

Пояснения:

И теперь последний член суммы. Мы помним, что ошибка и целевая переменная независимы друг от друга:

Наконец, собираем все вместе:

Итак, мы достигли цели всех вычислений, описанных выше, последняя формула говорит нам, что ошибка прогноза любой модели вида складывается из:

• квадрата смещения: – средняя ошибка по всевозможным наборам данных;
• дисперсии: – вариативность ошибки, то, на сколько ошибка будет отличаться, если обучать модель на разных наборах данных;
• неустранимой ошибки: .

Если с последней мы ничего сделать не можем, то на первые два слагаемых мы можем как-то влиять. В идеале, конечно же, хотелось бы свести на нет оба этих слагаемых (левый верхний квадрат рисунка), но на практике часто приходится балансировать между смещенными и нестабильными оценками (высокая дисперсия).

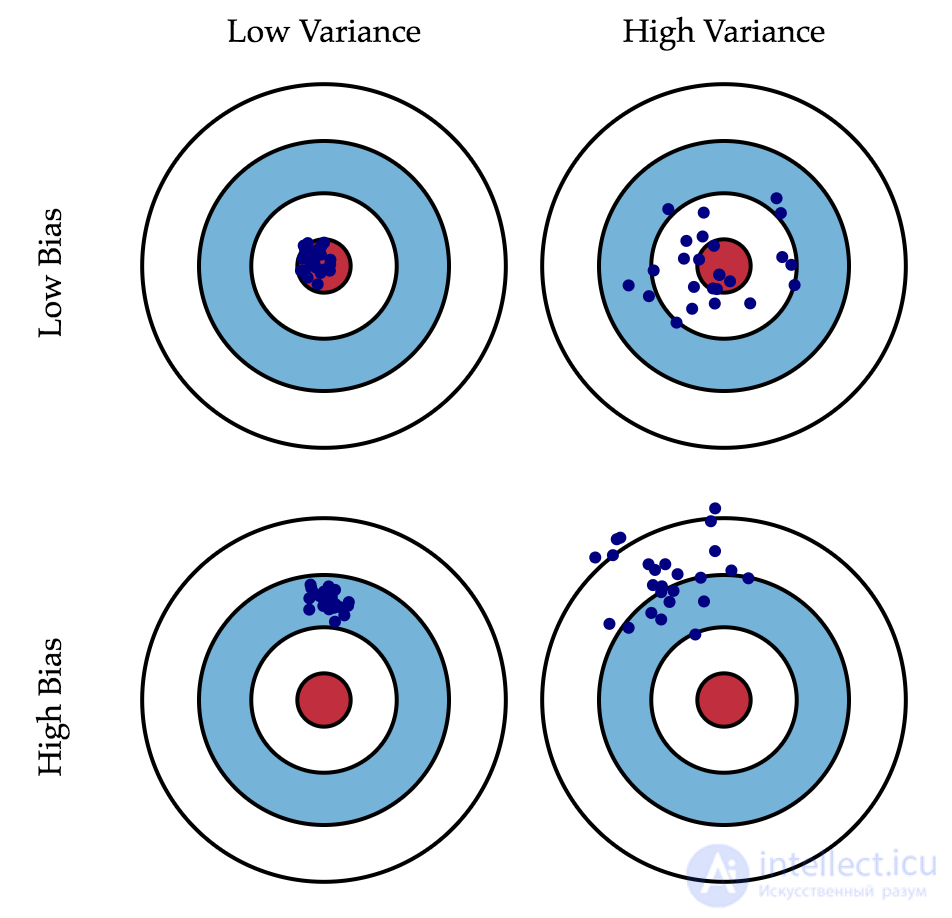
Как правило, при увеличении сложности модели (например, при увеличении количества свободных параметров) увеличивается дисперсия (разброс) оценки, но уменьшается смещение. Из-за того что тренировочный набор данных полностью запоминается вместо обобщения, небольшие изменения приводят к неожиданным результатам (переобучение). Если же модель слабая, то она не в состоянии выучить закономерность, в результате выучивается что-то другое, смещенное относительно правильного решения.

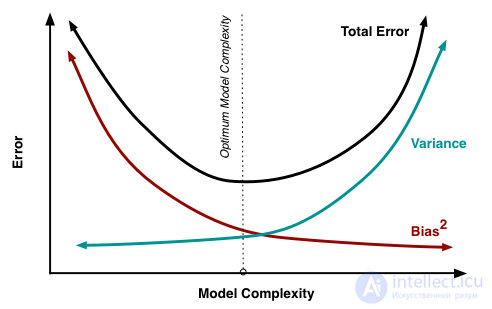
Теорема Маркова-Гаусса как раз утверждает, что МНК-оценка параметров линейной модели является самой лучшей в классе несмещенных линейных оценок, то есть с наименьшей дисперсией. Это значит, что если существует какая-либо другая несмещенная модель тоже из класса линейных моделей, то мы можем быть уверены, что .

Регуляризация линейной регрессии

Иногда бывают ситуации, когда мы намеренно увеличиваем смещенность модели ради ее стабильности, т.е. ради уменьшения дисперсии модели . Одним из условий теоремы Маркова-Гаусса является полный столбцовый ранг матрицы . В противном случае решение МНК не существует, т.к. не будет существовать обратная матрица Другими словами, матрица будет сингулярна, или вырожденна. Об этом говорит сайт https://intellect.icu . Такая задача называется некорректно поставленной. Задачу нужно скорректировать, а именно, сделать матрицу невырожденной, или регулярной (именно поэтому этот процесс называется регуляризацией). Чаще в данных мы можем наблюдать так называемую мультиколлинеарность — когда два или несколько признаков сильно коррелированы, в матрице это проявляется в виде "почти" линейной зависимости столбцов. Например, в задаче прогнозирования цены квартиры по ее параметрам "почти" линейная зависимость будет у признаков "площадь с учетом балкона" и "площадь без учета балкона". Формально для таких данных матрица будет обратима, но из-за мультиколлинеарности у матрицы некоторые собственные значения будут близки к нулю, а в обратной матрице появятся экстремально большие собственные значения, т.к. собственные значения обратной матрицы – это . Итогом такого шатания собственных значений станет нестабильная оценка параметров модели, т.е. добавление нового наблюдения в набор тренировочных данных приведет к совершенно другому решению. Иллюстрации роста коэффициентов вы найдете в одном из наших прошлых постов. Одним из способов регуляризации является регуляризация Тихонова, которая в общем виде выглядит как добавление нового члена к среднеквадратичной ошибке:

Часто матрица Тихонова выражается как произведение некоторого числа на единичную матрицу: . В этом случае задача минимизации среднеквадратичной ошибки становится задачей с ограничением на норму. Если продифференцировать новую функцию стоимости по параметрам модели, приравнять полученную функцию к нулю и выразить , то мы получим точное решение задачи.

Такая регрессия называется гребневой регрессией (ridge regression). А гребнем является как раз диагональная матрица, которую мы прибавляем к матрице , в результате получается гарантированно регулярная матрица.

Такое решение уменьшает дисперсию, но становится смещенным, т.к. минимизируется также и норма вектора параметров, что заставляет решение сдвигаться в сторону нуля. На рисунке ниже на пересечении белых пунктирных линий находится МНК-решение. Голубыми точками обозначены различные решения гребневой регрессии. Видно, что при увеличении параметра регуляризации решение сдвигается в сторону нуля.

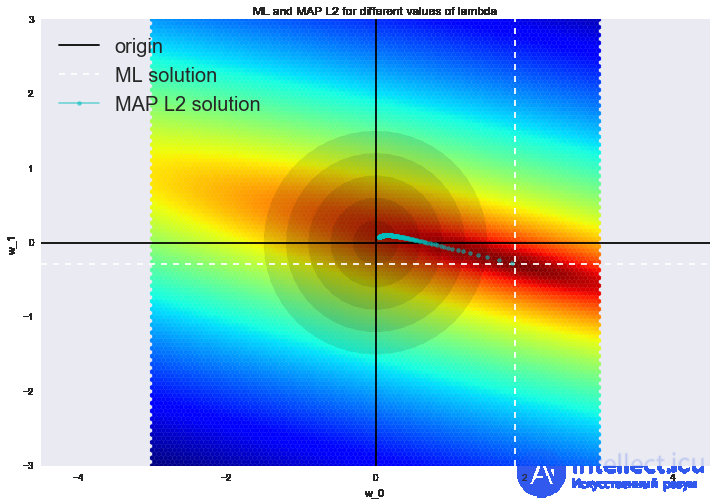
Советуем обратиться в наш прошлый пост за примером того, как регуляризация справляется с проблемой мультиколлинеарности, а также чтобы освежить в памяти еще несколько интерпретаций регуляризации.

2. Логистическая регрессия

Линейный классификатор

Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на два полупространства, в каждом из которых прогнозируется одно из двух значений целевого класса.
Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.

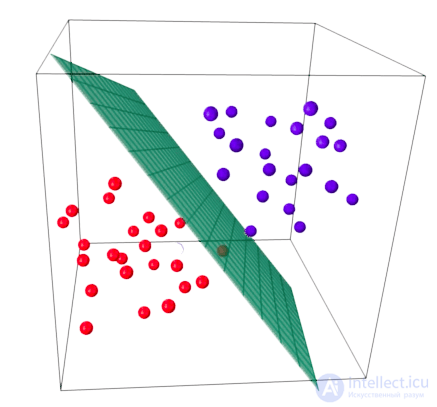
Мы уже знакомы с линейной регрессией и методом наименьших квадратов. Рассмотрим задачу бинарной классификации, причем метки целевого класса обозначим "+1" (положительные примеры) и "-1" (отрицательные примеры).
Один из самых простых линейных классификаторов получается на основе регрессии вот таким образом:

где

• – вектор признаков примера (вместе с единицей);
• – веса в линейной модели (вместе со смещением );
• – функция "сигнум", возвращающая знак своего аргумента;
• – ответ классификатора на примере .

Логистическая регрессия как линейный классификатор

Логистическая регрессия является частным случаем линейного классификатора, но она обладает хорошим "умением" – прогнозировать вероятность отнесения примера к классу "+":

Прогнозирование не просто ответа ("+1" или "-1"), а именно вероятности отнесения к классу "+1" во многих задачах является очень важным бизнес-требованием. Например, в задаче кредитного скоринга, где традиционно применяется логистическая регрессия, часто прогнозируют вероятность невозврата кредита (). Клиентов, обратившихся за кредитом, сортируют по этой предсказанной вероятности (по убыванию), и получается скоркарта — по сути, рейтинг клиентов от плохих к хорошим. Ниже приведен игрушечный пример такой скоркарты.

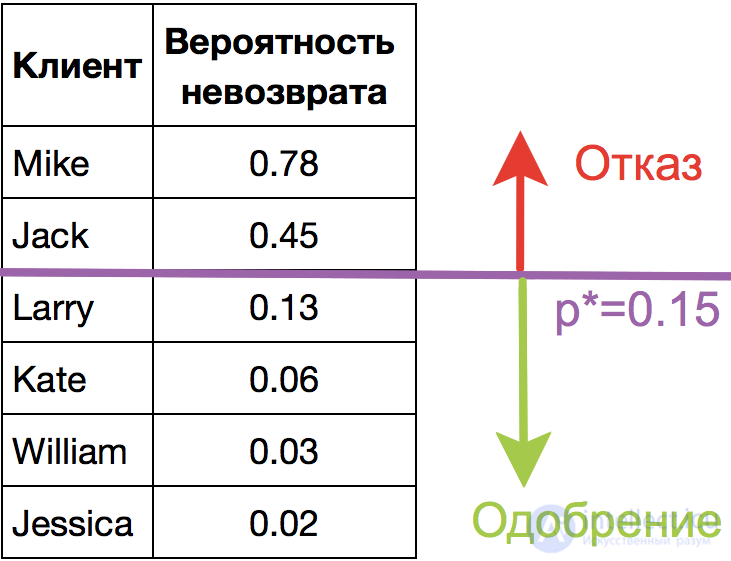
Банк выбирает для себя порог предсказанной вероятности невозврата кредита (на картинке – ) и начиная с этого значения уже не выдает кредит. Более того, можно умножить предсказанную вероятность на выданную сумму и получить матожидание потерь с клиента, что тоже будет хорошей бизнес-метрикой (Далее в комментариях специалисты по скорингу могут поправить, но главная суть примерно такая).

Итак, мы хотим прогнозировать вероятность , а пока умеем строить линейный прогноз с помощью МНК: . Каким образом преобразовать полученное значение в вероятность, пределы которой – [0, 1]? Очевидно, для этого нужна некоторая функция В модели логистической регрессии для этого берется конкретная функция: . И сейчас разберемся, каковы для этого предпосылки.

Обозначим вероятностью происходящего события . Тогда отношение вероятностей определяется из , а это — отношение вероятностей того, произойдет ли событие или не произойдет. Очевидно, что вероятность и отношение шансов содержат одинаковую информацию. Но в то время как находится в пределах от 0 до 1, находится в пределах от 0 до .

Если вычислить логарифм (то есть называется логарифм шансов, или логарифм отношения вероятностей), то легко заметить, что . Его-то мы и будем прогнозировать с помощью МНК.

Посмотрим, как логистическая регрессия будет делать прогноз (пока считаем, что веса мы как-то получили (т.е. обучили модель), далее разберемся, как именно).

• Шаг 1. Вычислить значение . (уравнение задает гиперплоскость, разделяющую примеры на 2 класса);

• Шаг 2. Вычислить логарифм отношения шансов: .

• Шаг 3. Имея прогноз шансов на отнесение к классу "+" – , вычислить с помощью простой зависимости:

В правой части мы получили как раз

продолжение следует...

Продолжение:

Часть 1 4. Линейные модели классификации и регрессии
Часть 2 3. Наглядный пример регуляризации логистической регрессии - 4. Линейные модели
Часть 3 5. Кривые валидации и обучения - 4. Линейные модели классификации

См.также

• Регрессия
• Принцип Харди – Вайнберга
• Внутренняя валидность
• Закон больших чисел
• Мартингейл
• Разбавление регрессии
• Критерий отбора
• Метод наименьших квадратов

Анализ данных, представленных в статье про линейные модели классификации, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое линейные модели классификации, линейная регрессия, логическая регрессия, регуляризация логистической регрессии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.