Лекция
Привет, Вы узнаете о том , что такое обратное распространение во времени, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обратное распространение во времени, bptt, bpts, обратное распространение через структуру , настоятельно рекомендую прочитать все из категории Машинное обучение.
обратное распространение во времени (BPTT) - это метод на основе градиента для обучения определенных типов рекуррентных нейронных сетей . Его можно использовать для обучения сетей Эльмана . Алгоритм был независимо разработан многочисленными исследователями.
Данные обучения для рекуррентной нейронной сети представляют собой упорядоченную последовательность 
пары ввода-вывода, 
. Для скрытого состояния необходимо указать начальное значение 
. Обычно для этой цели используется вектор всех нулей.
BPTT разворачивает повторяющуюся нейронную сеть во времени.
BPTT начинается с развертывания повторяющейся нейронной сети во времени. Развернутая сеть содержитвходы и выходы, но все копии сети имеют одни и те же параметры. Затем алгоритм обратного распространения ошибки используется для нахождения градиента стоимости по всем параметрам сети.
Рассмотрим пример нейронной сети, содержащей повторяющийся слой.
и слой с прямой связью
. Есть разные способы определения стоимости обучения, но общая стоимость всегда является средней стоимостью каждого временного шага. Стоимость каждого временного шага можно рассчитать отдельно. На рисунке выше показано, как стоимость во времени
можно вычислить, развернув повторяющийся слой для трех временных шагов и добавление слоя прямой связи . Каждый экземплярв развернутой сети имеет те же параметры. Об этом говорит сайт https://intellect.icu . Таким образом, вес обновляется в каждом случае (
) суммируются.
Псевдокод для усеченной версии BPTT, где обучающие данные содержат 
пары ввода-вывода, но сеть развернута на временные шаги:
BPTT имеет тенденцию быть значительно быстрее для обучения повторяющихся нейронных сетей, чем универсальные методы оптимизации, такие как эволюционная оптимизация.
BPTT испытывает трудности с локальным оптимумом. Для рекуррентных нейронных сетей локальные оптимумы представляют собой гораздо более серьезную проблему, чем для нейронных сетей с прямой связью. Периодическая обратная связь в таких сетях имеет тенденцию создавать хаотические отклики на поверхности ошибки, что приводит к частому возникновению локальных оптимумов и в плохих местах на поверхности ошибки.
Рисунок 1: Стандартный LRAAM (A) и BPTS архитектура (B).
Обратное распространение через структуру (BPTS) - это основанный на градиенте метод обучения рекурсивных нейронных сетей (надмножество рекуррентных нейронных сетей ), который подробно описан в статье 1996 года, написанной Кристофом Голлером и Андреасом Кюхлером. Представление структур в виде DAG-файлов. Давайте сначала подробнее рассмотрим способ кодирования структур с помощью Labeling Recursive Auto-Associative Memory (LRAAM) . Все виды рекурсивных символьных структур данных, к которым мы стремимся, могут быть отображены на маркированные направленные ациклические графы (НАГ) DAG, Мы не рассматриваем здесь циклические структуры.. Чтобы вычислить представление графа, сначала необходимо вычислить представления всех подграфов. На этапе обучения LRAAM для каждого узла одна фаза прямого распространения активаций и одна фаза обратного распространения (каждый через три уровня сети) ошибок за эпоху нужно. Выбор НАГ-представления для структур, которые позволяют представлять различные вхождения (под) структуры в обучающем наборе только как один узел может привести к значительному (даже экспоненциальное) снижение сложности стандартного LRAAM. Этот аргумент справедлив и для нашей архитектуры (см. раздел 3). Вместо того, чтобы выбирать древовидное представление, поэтому мы предпочитаем НАГ-подобное представление для наших терминов, как показано на Рис 2.
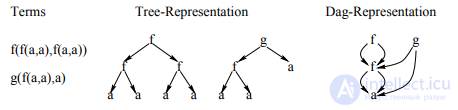
Рисунок 2: Дерево и DAG-представление набора терминов.
Для простоты мы сначала ограничимся древовидными структурами. в прямой фазе кодировщика (рис. 1, B) используется для вычисления представления для
дано дерево так же, как и в равнине LRAAM. Это делается путем рекурсивной передачи предыдущие вычисленные представления прямых поддеревьев на входном уровне кодировщика.
Этот процесс кодирования запускается на листьях дерева и генерирует представление для дерева, которое затем передается на следующий уровень, давая результат классификации на выходе Блока. Следующая метафора помогает нам объяснить обратную фазу. Представьте себе кодировщик
виртуально развернут (с скопированными весами) согласно древовидной структуре (см. рисунок 3).
Теперь ошибка, переданная от классификатора к скрытому слою, распространяется через развернутую сеть кодировщика.
Рисунок 3: Кодирующая сеть, развернутая структурой f (X; g (a; Y)).
Это развертывание по структуре аналогично развертыванию повторяющейся сети во времени (BPTT). побудило нас ввести термин обратное распространение через структуру (BPTS). Давайте сначала рассмотрим случай, когда для каждого появления (под) термина один выделенный узел в обучающей выборке зарезервирован (древовидное представление). Аргументируя аналогично BPTT [Wer90] мы видим, что вычисляется точный градиент. Представьте себе, что каждая копия
части кодировщика имеет собственный набор весов. Тогда по правильности обычного обратного распространения, вычисляется точный градиент. Если весовые матрицы разных копий идентифицированы, ясно, что нам просто нужно просуммировать компоненты, поступающие из разных копий, чтобы получить
точный градиент. Точная формулировка приведена ниже:
Для каждого (под) дерева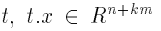 
является входным вектором кодировщика 
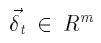вектор дельт (ошибок) для представления t, и Q
(t: x; t') проекция t: x на t поддерево t'
. Пусть далее W - матрица кодировщика, f ' производная передаточной функции и 
умножение двух векторов на компоненты.
Δ W рассчитывается как сумма по всем (под) деревьям (1). 
для каждого поддерева t' рассчитывается путем распространения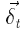 
одного определенного родительского узла t из t` обратно по (2):
Для каждого (под) дерева в обучающем наборе для одной эпохи требуется ровно одно прямое и одно
обратная фаза через энкодер. Тренировочная выборка статическая (без движущейся мишени).
Однако, если мы используем DAG-представление и представляем (под) структуру t только как один узел независимо от количества его вхождений, то могут быть разные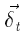 
в (1) и (2) для каждого вхождения t. Мы называем эту ситуацию - дельта-конфликтом. Предположим, что (под) структуры ti и tj идентичны. Конечно, это означает, что соответствующие подструктуры внутри ti и tj тоже идентичны. Это явно дает нам ti: x = tj: x, но у нас может быть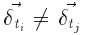 
Для вычисления Δ W нам понадобится только сумма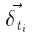 
и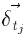 
. Об этом свидетельствуют следующее преобразование (1), которое выполняется из-за линейности умножения матриц:
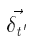с соответствующих детьми t` из ti и tj можно вычислить более эффективно, распространяю сумму 
и 
обратно в (2). Аналогичное преобразование (линейность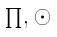 
и матричное умножение) для (2) показывает это.
Суммируя все различия, возникающие в каждом случае (под) структуры, получаем правильное (с самым крутым градиентом) решение дельта-конуса ict и позволяет очень эффективно реализовать BPTS для DAG. Нам просто нужно организовать узлы обучающего набора в топологическом порядке.
Прямая фаза начинается с листовых узлов и продолжается в обратном порядке, гарантируя, что представления для идентичных подструктур должны быть вычислены только один раз. Обратная фаза следует топологическому порядку, начиная с корневых узлов.
Таким образом, δ всех вхождений узла суммируются перед обработкой этого узла.. Опять же для каждого узла в обучающем наборе для одной эпохи требуется ровно одна прямая и одна обратная фаза через кодировщик.
Подобно стандартному распространению ошибки , BPTS можно использовать в пакетном или онлайн-режиме. BPTS-партия обновляет веса после того, как был представлен весь обучающий набор. Путем оптимизации методы, обсуждаемые в Разделе 3 (-суммирование и DAG-представление), каждый узел
нужно обрабатывать только один раз за эпоху. Это не относится к онлайн-режиму, потому что веса обновляются сразу после представления одной структуры и, следовательно, подструктуры должны обрабатываться для каждого случая отдельно.
Представленные результаты и исследования подтверждают, что применение искусственного интеллекта в области обратное распространение во времени имеет потенциал для революции в различных связанных с данной темой сферах. Надеюсь, что теперь ты понял что такое обратное распространение во времени, bptt, bpts, обратное распространение через структуру и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение
Из статьи мы узнали кратко, но содержательно про обратное распространение во времени
Комментарии
Оставить комментарий
Машинное обучение
Термины: Машинное обучение