5. Кривые валидации и обучения - 4. Линейные модели классификации

Это окончание невероятной информации про линейные модели классификации.

...

пространстве признаков и . В проекции на исходное пространство признаков граница получилась нелинейной.

На практике полиномиальные признаки действительно помогают, но строить их явно – вычислительно неэффективно. Гораздо быстрее работает SVM с ядровым трюком. При таком подходе в пространстве высокой размерности считается только расстояние между объектами (задаваемое функцией-ядром), а явно плодить комбинаторно большое число признаков не приходится. Про это подробно можно почитать в курсе Евгения Соколова (математика уже серьезная).

5. Кривые валидации и обучения

Мы уже получили представление о проверке модели, кросс-валидации и регуляризации.
Теперь рассмотрим главный вопрос:

Если качество модели нас не устраивает, что делать?

• Сделать модель сложнее или упростить?
• Добавить больше признаков?
• Или нам просто нужно больше данных для обучения?

Ответы на данные вопросы не всегда лежат на поверхности. В частности, иногда использование более сложной модели приведет к ухудшению показателей. Либо добавление наблюдений не приведет к ощутимым изменениям. Способность принять правильное решение и выбрать правильный способ улучшения модели, собственно говоря, и отличает хорошего специалиста от плохого.

Будем работать со знакомыми данными по оттоку клиентов телеком-оператора.

Импорт библиотек и чтение данных

from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns

import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV, SGDClassifier
from sklearn.model_selection import validation_curve

data = pd.read_csv('../../data/telecom_churn.csv').drop('State', axis=1)
data['International plan'] = data['International plan'].map({'Yes': 1, 'No': 0})
data['Voice mail plan'] = data['Voice mail plan'].map({'Yes': 1, 'No': 0})

y = data['Churn'].astype('int').values
X = data.drop('Churn', axis=1).values

Логистическую регрессию будем обучать стохастическим градиентным спуском. Пока объясним это тем, что так быстрее, но далее в программе у нас отдельная статья про это дело. Построим валидационные кривые, показывающие, как качество (ROC AUC) на обучающей и проверочной выборке меняется с изменением параметра регуляризации.

Код

alphas = np.logspace(-2, 0, 20)
sgd_logit = SGDClassifier(loss='log', n_jobs=-1, random_state=17)
logit_pipe = Pipeline([('scaler', StandardScaler()), ('poly', PolynomialFeatures(degree=2)), 
('sgd_logit', sgd_logit)])
val_train, val_test = validation_curve(logit_pipe, X, y,
'sgd_logit__alpha', alphas, cv=5,
scoring='roc_auc')

def plot_with_err(x, data, **kwargs):
mu, std = data.mean(1), data.std(1)
lines = plt.plot(x, mu, '-', **kwargs)
plt.fill_between(x, mu - std, mu + std, edgecolor='none',
facecolor=lines .get_color(), alpha=0.2)

plot_with_err(alphas, val_train, label='training scores')
plot_with_err(alphas, val_test, label='validation scores')
plt.xlabel(r'$\alpha$'); plt.ylabel('ROC AUC')
plt.legend();

Тенденция видна сразу, и она очень часто встречается.

• Для простых моделей тренировочная и валидационная ошибка находятся где-то рядом, и они велики. Это говорит о том, что модель недообучилась: то есть она не имеет достаточное кол-во параметров.

• Для сильно усложненных моделей тренировочная и валидационная ошибки значительно отличаются. Это можно объяснить переобучением: когда параметров слишком много либо не хватает регуляризации, алгоритм может "отвлекаться" на шум в данных и упускать основной тренд.

Сколько нужно данных?

Известно, что чем больше данных использует модель, тем лучше. Но как нам понять в конкретной ситуации, помогут ли новые данные? Скажем, целесообразно ли нам потратить N\$ на труд асессоров, чтобы увеличить выборку вдвое?

Поскольку новых данных пока может и не быть, разумно поварьировать размер имеющейся обучающей выборки и посмотреть, как качество решения задачи зависит от объема данных, на котором мы обучали модель. Так получаются кривые обучения (learning curves).

Идея простая: мы отображаем ошибку как функцию от количества примеров, используемых для обучения. При этом параметры модели фиксируются заранее.

Давайте посмотрим, что мы получим для линейной модели. Коэффициент регуляризации выставим большим.

Код

from sklearn.model_selection import learning_curve

def plot_learning_curve(degree=2, alpha=0.01):
train_sizes = np.linspace(0.05, 1, 20)
logit_pipe = Pipeline([('scaler', StandardScaler()), ('poly', PolynomialFeatures(degree=degree)), 
('sgd_logit', SGDClassifier(n_jobs=-1, random_state=17, alpha=alpha))])
N_train, val_train, val_test = learning_curve(logit_pipe,
X, y, train_sizes=train_sizes, cv=5,
scoring='roc_auc')
plot_with_err(N_train, val_train, label='training scores')
plot_with_err(N_train, val_test, label='validation scores')
plt.xlabel('Training Set Size'); plt.ylabel('AUC')
plt.legend()

plot_learning_curve(degree=2, alpha=10)

Типичная ситуация: для небольшого объема данных ошибки на обучающей выборке и в процессе кросс-валидации довольно сильно отличаются, что указывает на переобучение. Для той же модели, но с большим объемом данных ошибки "сходятся", что указывается на недообучение.

Если добавить еще данные, ошибка на обучающей выборке не будет расти, но с другой стороны, ошибка на тестовых данных не будет уменьшаться.

Получается, ошибки "сошлись", и добавление новых данных не поможет. Собственно, это случай – самый интересный для бизнеса. Возможна ситуация, когда мы увеличиваем выборку в 10 раз. Но если не менять сложность модели, это может и не помочь. То есть стратегия "настроил один раз – дальше использую 10 раз" может и не работать.

Что будет, если изменить коэффициент регуляризации (уменьшить до 0.05)?

Видим хорошую тенденцию – кривые постепенно сходятся, и если дальше двигаться направо (добавлять в модель данные), можно еще повысить качество на валидации.

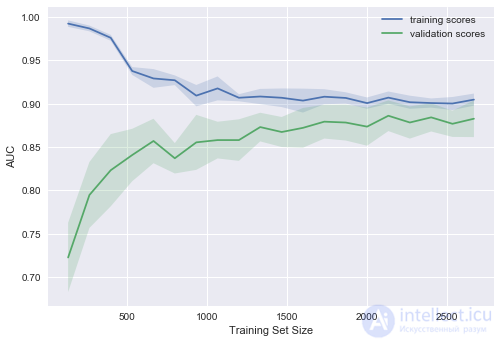
А если усложнить модель еще больше ()?

Проявляется переобучение – AUC падает как на обучении, так и на валидации.

Строя подобные кривые, можно понять, в какую сторону двигаться, и как правильно настроить сложность модели на новых данных.

Выводы по кривым валидации и обучения

• Ошибка на обучающей выборке сама по себе ничего не говорит о качестве модели
• Кросс-валидационная ошибка показывает, насколько хорошо модель подстраивается под данные (имеющийся тренд в данных), сохраняя при этом способность обобщения на новые данные
• Валидационная кривая представляет собой график, показывающий результат на тренировочной и валидационной выборке в зависимости от сложности модели:
• если две кривые распологаются близко, и обе ошибки велики, — это признак недообучения
• если две кривые далеко друг от друга, — это показатель переобучения
• Кривая обучения — это график, показывающий результаты на валидации и тренировочной подвыборке в зависимости от количества наблюдений:
• если кривые сошлись друг к другу, добавление новых данных не поможет – надо менять сложность модели
• если кривые еще не сошлись, добавление новых данных может улучшить результат.

6. Достоинства и недостатки линейных моделей в задачах машинного обучения

Плюсы:

• Хорошо изучены
• Очень быстрые, могут работать на очень больших выборках
• Практически вне конкуренции, когда признаков очень много (от сотен тысяч и более), и они разреженные (хотя есть еще факторизационные машины)
• Коэффициенты перед признаками могут интерпретироваться (при условии что признаки масштабированы) – в линейной регрессии как частные производные зависимой переменной от признаков, в логистической – как изменение шансов на отнесение к одному из классов в раз при изменении признака на 1 ед., подробнее тут
• Логистическая регрессия выдает вероятности отнесения к разным классам (это очень ценится, например, в кредитном скоринге)
• Модель может строить и нелинейную границу, если на вход подать полиномиальные признаки

Минусы:

• Плохо работают в задачах, в которых зависимость ответов от признаков сложная, нелинейная
• На практике предположения теоремы Маркова-Гаусса почти никогда не выполняются, поэтому чаще линейные методы работают хуже, чем, например, SVM и ансамбли (по качеству решения задачи классификации/регрессии)

7. Самостоятельная работа

Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.

В качестве закрепления изученного материала предлагаем следующее задание: разобраться с тем, как работает TfidfVectorizer и DictVectorizer, обучить и настроить модель линейной регрессии Ridge на данных о публикациях на Хабрахабре и воспроизвести бенчмарк в соревновании. Проверить себя можно отправив ответы в веб-форме (там же найдете и решение).

Вау!! 😲 Ты еще не читал? Это зря!

• Регрессия
• Принцип Харди – Вайнберга
• Внутренняя валидность
• Закон больших чисел
• Мартингейл
• Разбавление регрессии
• Критерий отбора
• Метод наименьших квадратов

Анализ данных, представленных в статье про линейные модели классификации, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое линейные модели классификации, линейная регрессия, логическая регрессия, регуляризация логистической регрессии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение

Продолжение:

Часть 1 4. Линейные модели классификации и регрессии
Часть 2 3. Наглядный пример регуляризации логистической регрессии - 4. Линейные модели
Часть 3 5. Кривые валидации и обучения - 4. Линейные модели классификации

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.