Лекция
Это продолжение увлекательной статьи про линейные модели классификации.
...
сигмоид-функцию.
Итак, логистическая регрессия прогнозирует вероятность отнесения примера к классу "+" (при условии, что мы знаем его признаки и веса модели) как сигмоид-преобразование линейной комбинации вектора весов модели и вектора признаков примера:
Следующий вопрос: как модель обучается? Тут мы опять обращаемся к принципу максимального правдоподобия.
Теперь посмотрим, как из принципа максимального правдоподобия получается оптимизационная задача, которую решает логистическая регрессия, а именно, – минимизация логистической функции потерь.
Только что мы увидели, что логистическая регрессия моделирует вероятность отнесения примера к классу "+" как
Тогда для класса "-" аналогичная вероятность:
Оба этих выражения можно ловко объединить в одно (следите за моими руками – не обманывают ли вас):
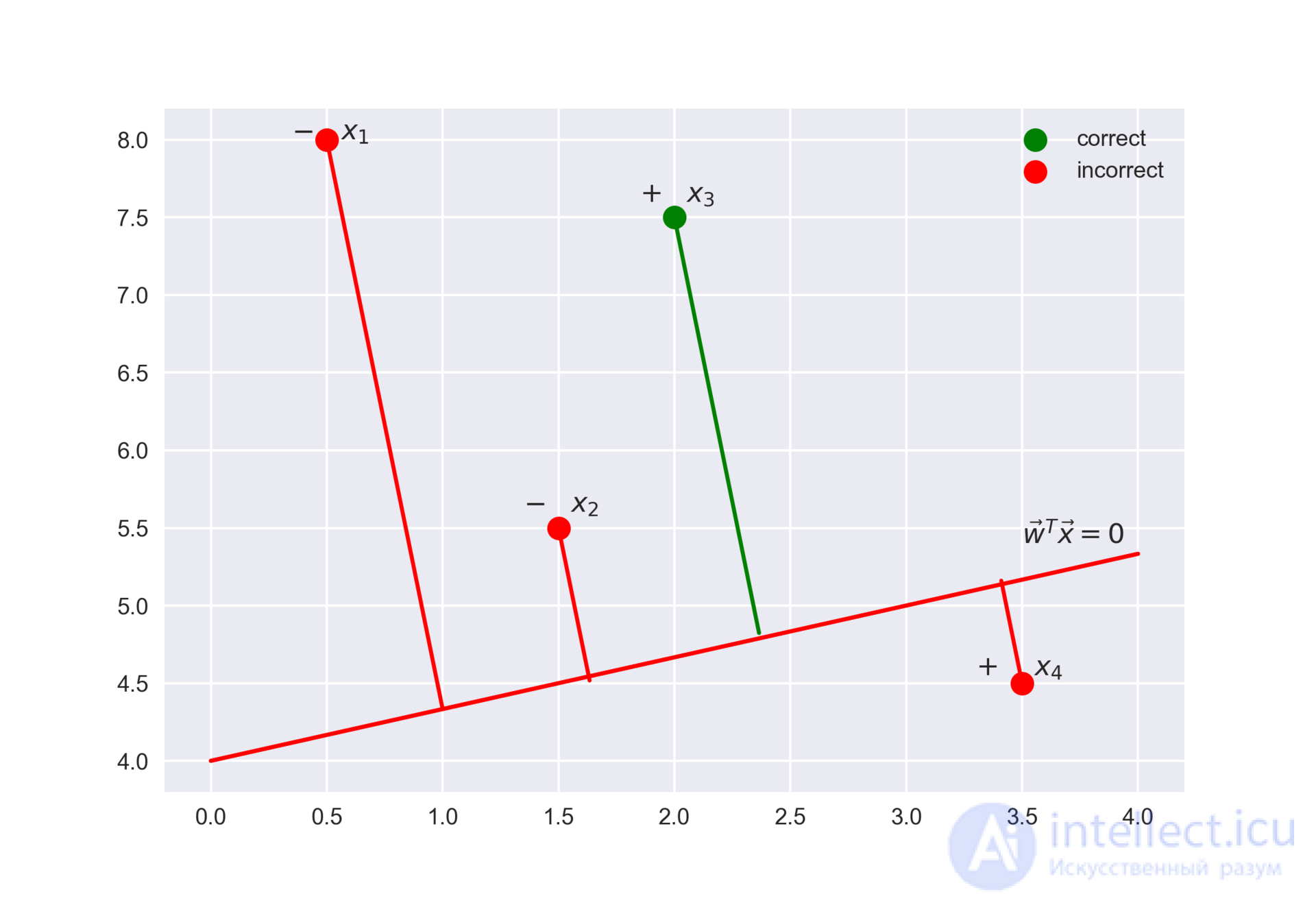
Выражение 
называется отступом (margin) классификации на объекте 
(не путать с зазором (тоже margin), про который чаще всего говорят в контексте SVM). Если он неотрицателен, модель не ошибается на объекте , если же отрицателен – значит, класс для спрогнозирован неправильно.
Заметим, что отступ определен для объектов именно обучающей выборки, для которых известны реальные метки целевого класса 
.
Чтобы понять, почему это мы сделали такие выводы, обратимся к геометрической интерпретации линейного классификатора. Подробно про это можно почитать в материалах Евгения Соколова.
Рекомендую решить почти классическую задачу из начального курса линейной алгебры: найти расстояние от точки с радиус-вектором 
до плоскости, которая задается уравнением 
Ответ
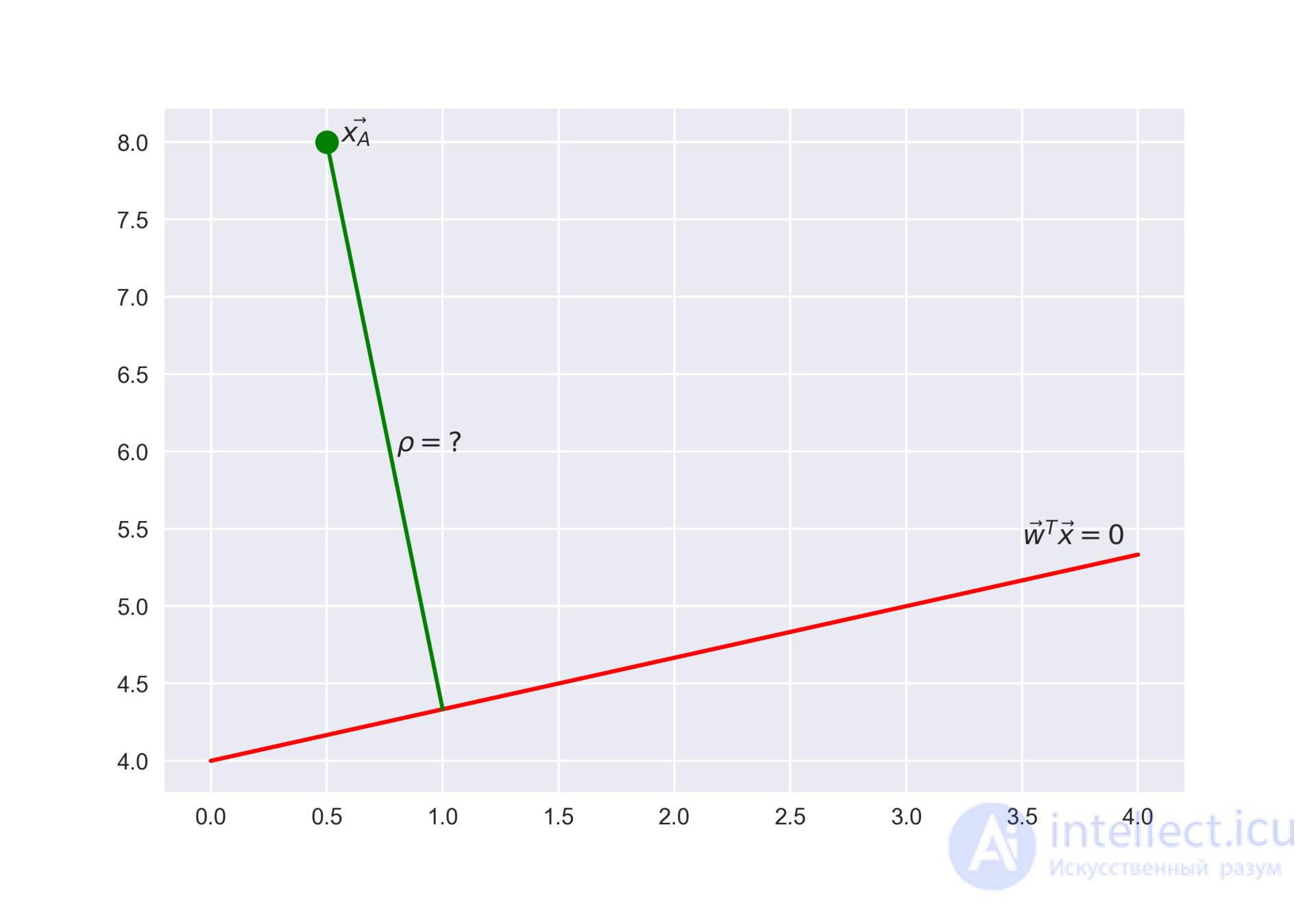
Когда получим (или посмотрим) ответ, то поймем, что чем больше по модулю выражение 
, тем дальше точка находится от плоскости
Значит, выражение – это своего рода "уверенность" модели в классификации объекта :
.
.
и 
.
Теперь распишем правдоподобие выборки, а именно, вероятность наблюдать данный вектор 
у выборки 
. Делаем сильное предположение: объекты приходят независимо, из одного распределения (i.i.d.). Тогда
где 
– длина выборки (число строк).
Как водится, возьмем логарифм данного выражения (сумму оптимизировать намного проще, чем произведение):
То есть в даном случае принцип максимизации правдоподобия приводит к минимизации выражения
Это логистическая функция потерь, просуммированная по всем объектам обучающей выборки.
Посмотрим на новую фунцию как на функцию от отступа: 
. Нарисуем ее график, а также график 1/0 функциий потерь (zero-one loss), которая просто штрафует модель на 1 за ошибку на каждом объекте (отступ отрицательный): 
.
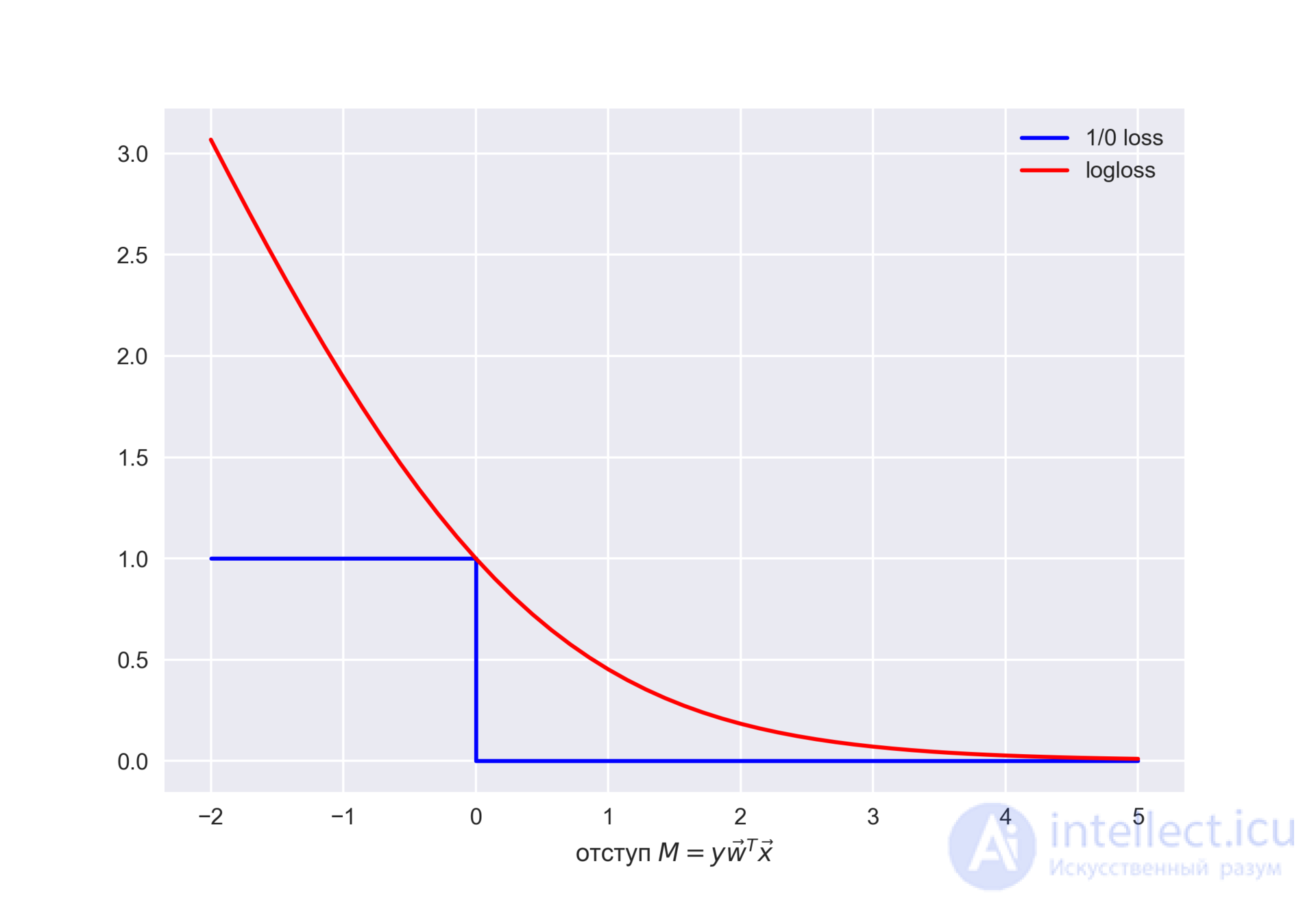
Картинка отражает общую идею, что в задаче классификации, не умея напрямую минимизировать число ошибок (по крайней мере, градиентными методами это не сделать – производная 1/0 функциий потерь в нуле обращается в бесконечность), мы минимизируем некоторую ее верхнюю оценку. В данном случае это логистическая функция потерь (где логарифм двоичный, но это не принципиально), и справедливо
где 
– попросту число ошибок логистической регрессии с весами 
на выборке 
.
То есть уменьшая верхнюю оценку 
на число ошибок классификации, мы таким образом надеемся уменьшить и само число ошибок.
-регуляризация логистических потерь
L2-
регуляризация логистической регрессии устроена почти так же, как и в случае с гребневой (Ridge регрессией). Вместо функционала 
минимизируется следующий:
В случае логистической регрессии принято введение обратного коэффициента регуляризации 
. И тогда решением задачи будет
Далее рассмотрим пример, позволяющий интуитивно понять один из смыслов регуляризации.
В 1 статье уже приводился пример того, как полиномиальные признаки позволяют линейным моделям строить нелинейные разделяющие поверхности. Покажем это в картинках.
Посмотрим, как регуляризация влияет на качество классификации на наборе данных по тестированию микрочипов из курса Andrew Ng по машинному обучению.
Будем использовать логистическую регрессию с полиномиальными признаками и варьировать параметр регуляризации C.
Сначала посмотрим, как регуляризация влияет на разделяющую границу классификатора, интуитивно распознаем переобучение и недообучение.
Потом численно установим близкий к оптимальному параметр регуляризации с помощью кросс-валидации (cross-validation) и перебора по сетке (GridSearch).
Подключение библиотек
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
%matplotlib inline
from matplotlib import pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LogisticRegression, LogisticRegressionCV
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.model_selection import GridSearchCV
Загружаем данные с помощью метода read_csv библиотеки pandas. В этом наборе данных для 118 микрочипов (объекты) указаны результаты двух тестов по контролю качества (два числовых признака) и сказано, пустили ли микрочип в производство. Признаки уже центрированы, то есть из всех значений вычтены средние по столбцам. Таким образом, "среднему" микрочипу соответствуют нулевые значения результатов тестов.
Загрузка данных
data = pd.read_csv('../../data/microchip_tests.txt',
header=None, names = ('test1','test2','released'))
# информация о наборе данных
data.info()
RangeIndex: 118 entries, 0 to 117
Data columns (total 3 columns):
test1 118 non-null float64
test2 118 non-null float64
released 118 non-null int64
dtypes: float64(2), int64(1)
memory usage: 2.8 KB
Посмотрим на первые и последние 5 строк.
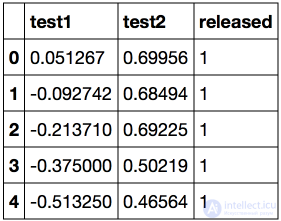
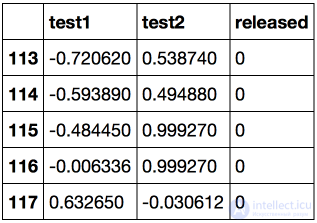
Сохраним обучающую выборку и метки целевого класса в отдельных массивах NumPy. Отобразим данные. Красный цвет соответствует бракованным чипам, зеленый – нормальным.
Код
X = data.ix[:,:2].values y = data.ix[:,2].values
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов')
plt.legend();
Определяем функцию для отображения разделяющей кривой классификатора
Код
def plot_boundary(clf, X, y, grid_step=.01, poly_featurizer=None): x_min, x_max = X[:, 0].min() - .1, X[:, 0].max() + .1 y_min, y_max = X[:, 1].min() - .1, X[:, 1].max() + .1 xx, yy = np.meshgrid(np.arange(x_min, x_max, grid_step), np.arange(y_min, y_max, grid_step)) # каждой точке в сетке [x_min, m_max]x[y_min, y_max] # ставим в соответствие свой цвет Z = clf.predict(poly_featurizer.transform(np.c_[xx.ravel(), yy.ravel()])) Z = Z.reshape(xx.shape) plt.contour(xx, yy, Z, cmap=plt.cm.Paired)
Полиномиальными признаками до степени 
для двух переменных и мы называем следующие:
Например, для 
это будут следующие признаки:
Нарисовав треугольник Пифагора, Вы сообразите, сколько таких признаков будет для 
и вообще для любого .
Попросту говоря, таких признаков экспоненциально много, и строить, скажем, для 100 признаков полиномиальные степени 10 может оказаться затратно (а более того, и не нужно).
Создадим объект sklearn, который добавит в матрицу полиномиальные признаки вплоть до степени 7 и обучим логистическую регрессию с параметром регуляризации 
. Изобразим разделяющую границу.
Также проверим долю правильных ответов классификатора на обучающей выборке. Видим, что регуляризация оказалась слишком сильной, и модель "недообучилась". Доля правильных ответов классификатора на обучающей выборке оказалась равной 0.627.
Код
poly = PolynomialFeatures(degree=7) X_poly = poly.fit_transform(X)
C = 1e-2
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.01, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=0.01')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))
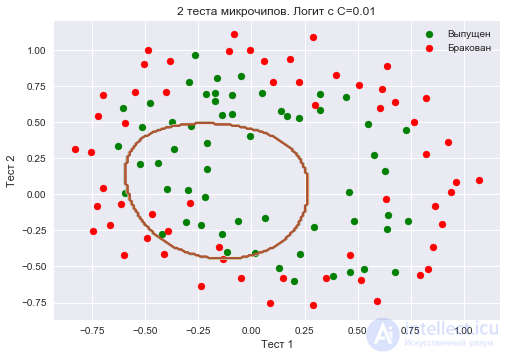
Увеличим 
до 1. Тем самым мы ослабляем регуляризацию, теперь в решении значения весов логистической регрессии могут оказаться больше (по модулю), чем в прошлом случае. Теперь доля правильных ответов классификатора на обучающей выборке – 0.831.
Код
C = 1
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.005, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=1')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))
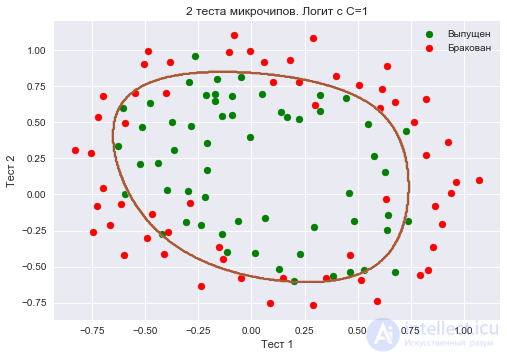
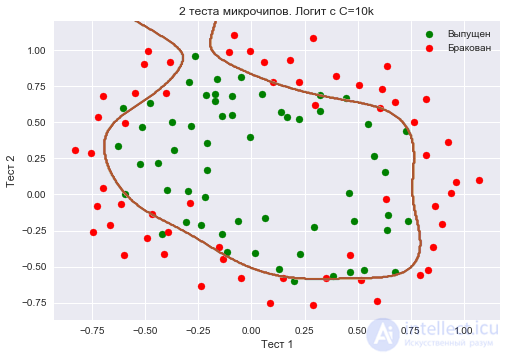
Еще увеличим – до 10 тысяч. Теперь регуляризации явно недостаточно, и мы наблюдаем переобучение. Можно заметить, что в прошлом случае (при =1 и "гладкой" границе) доля правильных ответов модели на обучающей выборке не намного ниже, чем в 3 случае, зато на новой выборке, можно себе представить, 2 модель сработает намного лучше.
Доля правильных ответов классификатора на обучающей выборке – 0.873.
Код
C = 1e4
logit = LogisticRegression(C=C, n_jobs=-1, random_state=17)
logit.fit(X_poly, y)
plot_boundary(logit, X, y, grid_step=.005, poly_featurizer=poly)
plt.scatter(X[y == 1, 0], X[y == 1, 1], c='green', label='Выпущен')
plt.scatter(X[y == 0, 0], X[y == 0, 1], c='red', label='Бракован')
plt.xlabel("Тест 1")
plt.ylabel("Тест 2")
plt.title('2 теста микрочипов. Логит с C=10k')
plt.legend();
print("Доля правильных ответов классификатора на обучающей выборке:",
round(logit.score(X_poly, y), 3))
Чтоб обсудить результаты, перепишем формулу для функционала, который оптимизируется в логистической регрессии, в таком виде:
где
– логистическая функция потерь, просуммированная по всей выборке – обратный коэффициент регуляризации (тот самый в sklearn-реализации LogisticRegression)
Промежуточные выводы:
, тем более сложные зависимости в данных может восстанавливать модель (интуитивно соответствует "сложности" модели (model capacity))), то решением задачи минимизации логистической функции потерь может оказаться то, когда многие веса занулились или стали слишком малыми. Еще говорят, что модель недостаточно "штрафуется" за ошибки (то есть в функционале 
"перевешивает" сумма квадратов весов, а ошибка может быть относительно большой). В таком случае модель окажется недообученной (1 случай)), то решением задачи оптимизации может стать вектор 
с большими по модулю компонентами. В таком случае больший вклад в оптимизируемый функционал имеет и, вольно выражаясь, модель слишком "боится" ошибиться на объектах обучающей выборки, поэтому окажется переобученной (3 случай) выбрать, сама логистическая регрессия "не поймет" (или еще говорят "не выучит"), то есть это не может быть определено решением оптимизационной задачи, которой является логистическая регрессия (в отличие от весов ). Так же точно, дерево решений не может "само понять", какое ограничение на глубину выбрать (за один процесс обучения). Поэтому – это гиперпараметр модели, который настраивается на кросс-валидации, как и max_depth для дерева.
Настройка параметра регуляризации
Теперь найдем оптимальное (в данном примере) значение параметра регуляризации . Сделать это можно с помощью LogisticRegressionCV – перебора параметров по сетке с последующей кросс-валидацией. Этот класс создан специально для логистической регрессии (для нее известны эффективные алгоритмы перебора параметров), для произвольной модели мы бы использовали GridSearchCV, RandomizedSearchCV или, например, специальные алгоритмы оптимизации гиперпараметров, реализованные в hyperopt.
Код
skf = StratifiedKFold(n_splits=5, shuffle=True, random_state=17) c_values = np.logspace(-2, 3, 500) logit_searcher = LogisticRegressionCV(Cs=c_values, cv=skf, verbose=1, n_jobs=-1) logit_searcher.fit(X_poly, y)
Посмотрим, как качество модели (доля правильных ответов на обучающей и валидационной выборках) меняется при изменении гиперпараметра .
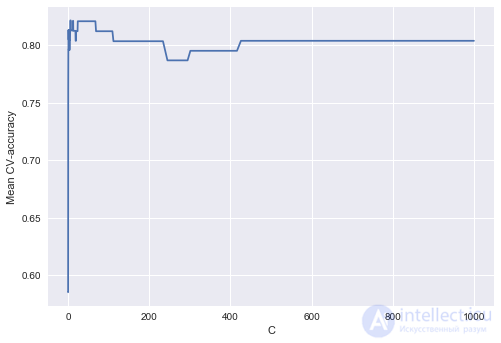
Выделим участок с "лучшими" значениями C.
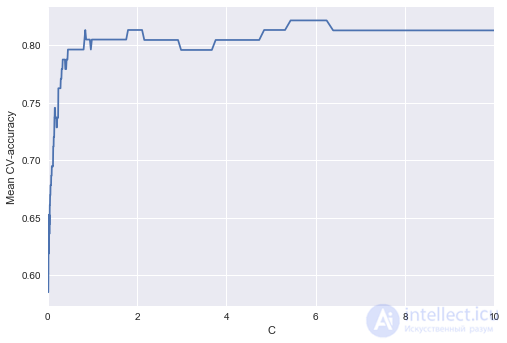
Как мы помним, такие кривые называются валидационными, раньше мы их строили вручную, но в sklearn для них их построения есть специальные методы, которые мы тоже сейчас будем использовать.
Будем решать задачу бинарной классификации отзывов IMDB к фильмам. Имеется обучающая выборка с размеченными отзывами, по 12500 отзывов известно, что они хорошие, еще про 12500 – что они плохие. Здесь уже не так просто сразу приступить к машинному обучению, потому что готовой матрицы нет – ее надо приготовить. Будем использовать самый простой подход – мешок слов ("Bag of words"). При таком подходе признаками отзыва будут индикаторы наличия в нем каждого слова из всего корпуса, где корпус – это множество всех отзывов. Идея иллюстрируется картинкой
Импорт библиотек и загрузка данных
from __future__ import division, print_function
# отключим всякие предупреждения Anaconda
import warnings
warnings.filterwarnings('ignore')
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import numpy as np
from sklearn.datasets import load_files
from sklearn.feature_extraction.text import CountVectorizer, TfidfTransformer, TfidfVectorizer
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
Загрузим данные отсюда (краткое описание — тут). В обучающей и тестовой выборках по 12500 тысяч хороших и плохих отзывов к фильмам.
reviews_train = load_files("YOUR PATH")
text_train, y_train = reviews_train.data, reviews_train.target
print("Number of documents in training data: %d" % len(text_train))
print(np.bincount(y_train))
# поменяйте путь к файлу
reviews_test = load_files("YOUR PATH")
text_test, y_test = reviews_test.data, reviews_test.target
print("Number of documents in test data: %d" % len(text_test))
print(np.bincount(y_test))
Пример плохого отзыва:
'Words can\'t describe how bad this movie is. I can\'t explain it by writing only. You have too see it for yourself to get at grip of how horrible a movie really can be. Not that I recommend you to do that. There are so many clich , mistakes (and all other negative things you can imagine) here that will just make you cry. To start with the technical first, there are a LOT of mistakes regarding the airplane. I won\'t list them here, but just mention the coloring of the plane. They didn\'t even manage to show an airliner in the colors of a fictional airline, but instead used a 7479 painted in the original Boeing livery. Very bad. The plot is stupid and has been done many times before, only much, much better. There are so many ridiculous moments here that i lost count of it really early. Also, I was on the bad guys\' side all the time in the movie, because the good guys were so stupid. "Executive Decision" should without a doubt be you\'re choice over this one, even the "Turbulence"-movies are better. In fact, every other movie in the world is better than this one.'
Невозможно описать словами, насколько плох этот фильм. Я не могу объяснить это только письмом. Вы тоже должны убедиться в этом сами, чтобы понять, насколько ужасным может быть фильм. Не то чтобы я рекомендовал вам это делать. Здесь так много клише , ошибок (и всего прочего негативного, что вы можете себе представить), что заставит вас плакать. Начнем с технических вопросов. В отношении самолета есть МНОГО ошибок. Я не буду их здесь перечислять, а упомяну лишь расцветку самолета. Им даже не удалось показать авиалайнер в цветах вымышленной авиакомпании, а вместо этого использовали 7479, окрашенный в оригинальную ливрею Boeing. Очень плохо. Сюжет тупой, и раньше его делали много раз, только намного лучше. Здесь так много смешных моментов, что я очень рано потерял счет. Кроме того, я все время был на стороне плохих парней в фильме, потому что хорошие парни были такими глупыми. "Исполнительное решение", без сомнения, должно быть вашим выбором вместо этого, даже фильмы "Турбулентность" лучше. Фактически, любой другой фильм в мире лучше, чем этот ».
Пример хорошего отзыва:
'Everyone plays their part pretty well in this "little nice movie". Belushi gets the chance to live part of his life differently, but ends up realizing that what he had was going to be just as good or maybe even better. The movie shows us that we ought to take advantage of the opportunities we have, not the ones we do not or cannot have. If U can get this movie on video for around $10, it\xc2\xb4d be an investment!'
«Каждый хорошо играет свою роль в этом« маленьком красивом фильме ». Белуши получает шанс прожить часть своей жизни по-другому, но в итоге понимает, что то, что у него было, будет таким же хорошим, а может быть, даже лучше. Фильм показывает нам, что мы должны использовать возможности, которые у нас есть, а не те, которых у нас нет или не может быть. Если вы сможете снять этот фильм на видео примерно за 10 долларов, это будет вложением денег! '
Составим словарь всех слов с помощью CountVectorizer. Всего в выборке 74849 уникальных слов. Если посмотреть на примеры полученных "слов" (лучше их называть токенами), то можно увидеть, что многие важные этапы обработки текста мы тут пропустили (автоматическая обработка текстов – это могло бы быть темой отдельной серии статей).
Код
cv = CountVectorizer() cv.fit(text_train) print(len(cv.vocabulary_)) #74849
print(cv.get_feature_names()[:50]) print(cv.get_feature_names()[50000:50050])
['00', '000', '0000000000001', '00001', '00015', '000s', '001', '003830', '006', '007', '0079', '0080', '0083', '0093638', '00am', '00pm', '00s', '01', '01pm', '02', '020410', '029', '03', '04', '041', '05', '050', '06', '06th', '07', '08', '087', '089', '08th', '09', '0f', '0ne', '0r', '0s', '10', '100', '1000', '1000000', '10000000000000', '1000lb', '1000s', '1001', '100b', '100k', '100m']
['pincher', 'pinchers', 'pinches', 'pinching', 'pinchot', 'pinciotti', 'pine', 'pineal', 'pineapple', 'pineapples', 'pines', 'pinet', 'pinetrees', 'pineyro', 'pinfall', 'pinfold', 'ping', 'pingo', 'pinhead', 'pinheads', 'pinho', 'pining', 'pinjar', 'pink', 'pinkerton', 'pinkett', 'pinkie', 'pinkins', 'pinkish', 'pinko', 'pinks', 'pinku', 'pinkus', 'pinky', 'pinnacle', 'pinnacles', 'pinned', 'pinning', 'pinnings', 'pinnochio', 'pinnocioesque', 'pino', 'pinocchio', 'pinochet', 'pinochets', 'pinoy', 'pinpoint', 'pinpoints', 'pins', 'pinsent']
Закодируем предложения из текстов обучающей выборки индексами входящих слов. Используем разреженный формат. Преобразуем так же тестовую выборку.
X_train = cv.transform(text_train) X_test = cv.transform(text_test)
Обучим логистическую регрессию и посмотрим на доли правильных ответов на обучающей и тестовой выборках. Получается, на тестовой выборке мы правильно угадываем тональность примерно 86.7% отзывов.
Код
%%time logit = LogisticRegression(n_jobs=-1, random_state=7) logit.fit(X_train, y_train) print(round(logit.score(X_train, y_train), 3), round(logit.score(X_test, y_test), 3))
Коэффициенты модели можно красиво отобразить.
Код визуализации коэффициентов модели
def visualize_coefficients(classifier, feature_names, n_top_features=25): # get coefficients with large absolute values coef = classifier.coef_.ravel() positive_coefficients = np.argsort(coef)[-n_top_features:] negative_coefficients = np.argsort(coef)[:n_top_features] interesting_coefficients = np.hstack([negative_coefficients, positive_coefficients]) # plot them plt.figure(figsize=(15, 5)) colors = ["red" if c < 0 else "blue" for c in coef[interesting_coefficients]] plt.bar(np.arange(2 * n_top_features), coef[interesting_coefficients], color=colors) feature_names = np.array(feature_names) plt.xticks(np.arange(1, 1 + 2 * n_top_features), feature_names[interesting_coefficients], rotation=60, ha="right");
def plot_grid_scores(grid, param_name): plt.plot(grid.param_grid[param_name], grid.cv_results_['mean_train_score'], color='green', label='train') plt.plot(grid.param_grid[param_name], grid.cv_results_['mean_test_score'], color='red', label='test') plt.legend();
visualize_coefficients(logit, cv.get_feature_names())
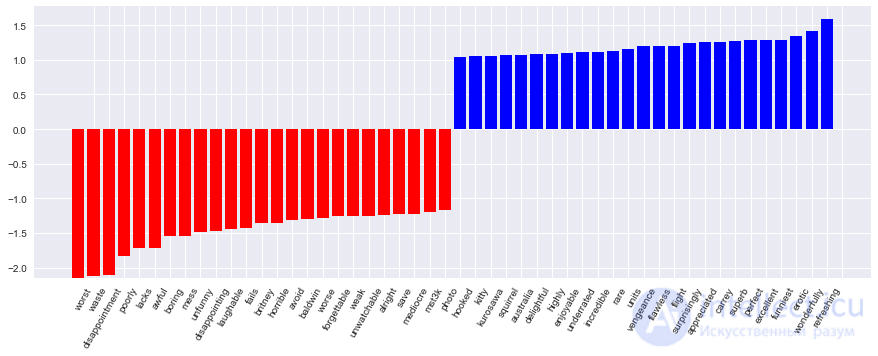
Подберем коэффициент регуляризации для логистической регрессии. Используем sklearn.pipeline, поскольку CountVectorizer правильно применять только на тех данных, на которых в текущий момент обучается модель (чтоб не "подсматривать" в тестовую выборку и не считать по ней частоты вхождения слов). В данном случае pipeline задает последовательность действий: применить CountVectorizer, затем обучить логистическую регрессию. Так мы поднимаем долю правильных ответов до 88.5% на кросс-валидации и 87.9% – на отложенной выборке.
Код
from sklearn.pipeline import make_pipeline
text_pipe_logit = make_pipeline(CountVectorizer(),
LogisticRegression(n_jobs=-1, random_state=7))
text_pipe_logit.fit(text_train, y_train)
print(text_pipe_logit.score(text_test, y_test))
from sklearn.model_selection import GridSearchCV
param_grid_logit = {'logisticregression__C': np.logspace(-5, 0, 6)}
grid_logit = GridSearchCV(text_pipe_logit, param_grid_logit, cv=3, n_jobs=-1)
grid_logit.fit(text_train, y_train)
grid_logit.best_params_, grid_logit.best_score_
plot_grid_scores(grid_logit, 'logisticregression__C')
grid_logit.score(text_test, y_test)
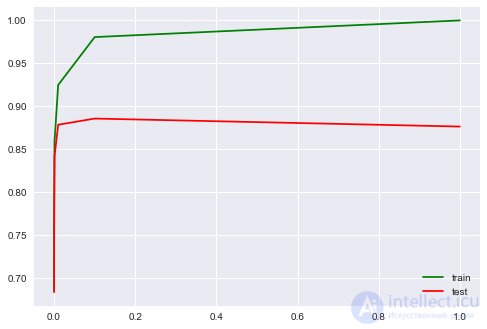
Теперь то же самое, но со случайным лесом. Видим, что с логистической регрессией мы достигаем большей доли правильных ответов меньшими усилиями. Лес работает дольше, на отложенной выборке 85.5% правильных ответов.
Код для обучения случайного леса
from sklearn.ensemble import RandomForestClassifier forest = RandomForestClassifier(n_estimators=200, n_jobs=-1, random_state=17) forest.fit(X_train, y_train) print(round(forest.score(X_test, y_test), 3))
Теперь рассмотрим пример, где линейные модели справляются хуже.
Линейные методы классификации строят все же очень простую разделяющую поверхность – гиперплоскость. Самый известный игрушечный пример, в котором классы нельзя без ошибок поделить гиперплоскостью (то есть прямой, если это 2D), получил имя "the XOR problem".
XOR – это "исключающее ИЛИ", булева функция со следующей таблицей истинности:
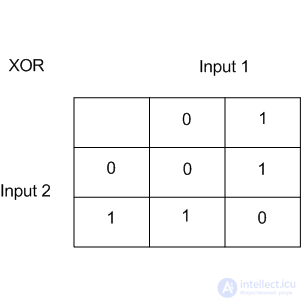
XOR дал имя простой задаче бинарной классификации, в которой классы представлены вытянутыми по диагоналям и пересекающимися облаками точек.
Код, рисующий следующие 3 картинки
# порождаем данные rng = np.random.RandomState(0) X = rng.randn(200, 2) y = np.logical_xor(X[:, 0] > 0, X[:, 1] > 0)
plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=plt.cm.Paired);
def plot_boundary(clf, X, y, plot_title): xx, yy = np.meshgrid(np.linspace(-3, 3, 50), np.linspace(-3, 3, 50)) clf.fit(X, y) # plot the decision function for each datapoint on the grid Z = clf.predict_proba(np.vstack((xx.ravel(), yy.ravel())).T)[:, 1] Z = Z.reshape(xx.shape) image = plt.imshow(Z, interpolation='nearest', extent=(xx.min(), xx.max(), yy.min(), yy.max()), aspect='auto', origin='lower', cmap=plt.cm.PuOr_r) contours = plt.contour(xx, yy, Z, levels= , linewidths=2, linetypes='--') plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=plt.cm.Paired) plt.xticks(()) plt.yticks(()) plt.xlabel(r'$$') plt.ylabel(r'$$') plt.axis([-3, 3, -3, 3]) plt.colorbar(image) plt.title(plot_title, fontsize=12);
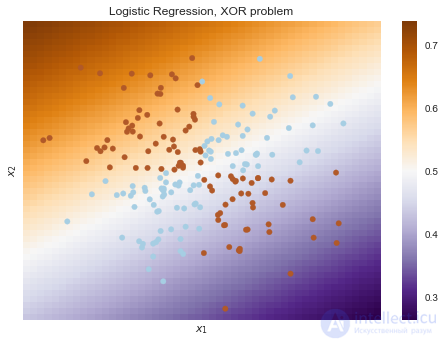
plot_boundary(LogisticRegression(), X, y, "Logistic Regression, XOR problem")
from sklearn.preprocessing import PolynomialFeatures from sklearn.pipeline import Pipeline
logit_pipe = Pipeline([('poly', PolynomialFeatures(degree=2)),
('logit', LogisticRegression())])
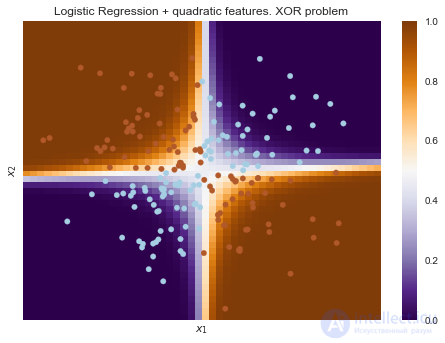
plot_boundary(logit_pipe, X, y, "Logistic Regression + quadratic features. XOR problem")
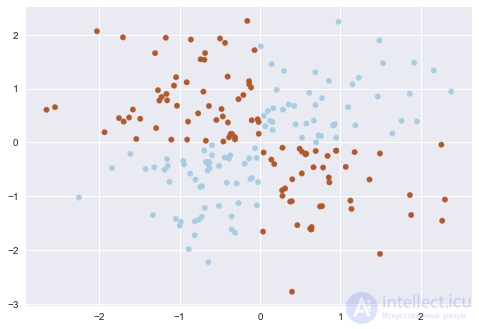
Очевидно, нельзя провести прямую так, чтобы без ошибок отделить один класс от другого. Поэтому логистическая регрессия плохо справляется с такой задачей.
А вот если на вход подать полиномиальные признаки, в данном случае до 2 степени, то проблема решается.
Здесь логистическая регрессия все равно строила гиперплоскость, но в 6-мерном
продолжение следует...
Часть 1 4. Линейные модели классификации и регрессии
Часть 2 3. Наглядный пример регуляризации логистической регрессии - 4. Линейные модели
Часть 3 5. Кривые валидации и обучения - 4. Линейные модели классификации
Анализ данных, представленных в статье про линейные модели классификации, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое линейные модели классификации, линейная регрессия, логическая регрессия, регуляризация логистической регрессии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение
Комментарии
Оставить комментарий
Машинное обучение
Термины: Машинное обучение