Лекция
Привет, Вы узнаете о том , что такое цикломатическая сложность, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое цикломатическая сложность, цикломатическое число , настоятельно рекомендую прочитать все из категории Качество и тестирование программного обеспечения. Quality Assurance..
цикломатическая сложность программы (англ. cyclomatic complexity of a program) — структурная (или топологическая) мера сложности компьютерной программы. Мера была разработана Томасом Дж. Маккейбом в 1976 году.
При вычислении цикломатической сложности используется граф потока управления программы. Узлы графа соответствуют неделимым группам команд программы, они соединены ориентированными ребрами, если группа команд, соответствующая второму узлу, может быть выполнена непосредственно после группы команд первого узла. Цикломатическая сложность может быть также вычислена для отдельных функций, модулей, методов или классов в пределах программы.
Маккейб применял вычисление цикломатической сложности при тестировании. Предложенный им метод заключался в тестировании каждого линейно независимого маршрута через программу, в этом случае число необходимых тестов равно цикломатической сложности программы.
Цикломатическая сложность части программного кода — количество линейно независимых маршрутов через программный код. Например, если исходный код не содержит никаких точек ветвления или циклов, то сложность равна единице, поскольку есть только единственный маршрут через код. Если код имеет единственный оператор IF, содержащий простое условие, то существует два пути через код: один если условие оператора IF имеет значение TRUE и один — если FALSE.
Математически цикломатическая сложность структурированной программы определяется с помощью ориентированного графа, узлами которого являются блоки программы, соединенные ребрами, если управление может переходить с одного блока на другой. Тогда сложность определяется как: :
M = E − N + 2P,
где:
M = цикломатическая сложность,
E = количество ребер в графе,
N = количество узлов в графе,
P = количество компонент связности.
В другой формулировке используется граф, в котором каждая точка выхода соединена с точкой входа. В этом случае граф является сильносвязным, и цикломатическая сложность программы равна цикломатическому числу этого графа (также известному как первое число Бетти), которое определяется как
M = E − N + P.
Это определение может рассматриваться как вычисление числа линейно независимых циклов, которые существуют в графе, то есть тех циклов, которые не содержат в себе других циклов. Так как каждая точка выхода соединена с точкой входа, то существует по крайней мере один цикл для каждой точки выхода.
Для простой программы, или подпрограммы, или метода P всегда равно 1. Однако цикломатическая сложность может применяться к нескольким таким программам или подпрограммам (например, ко всем методам в классе), в таком случае P равно числу подпрограмм, о которых идет речь, так как каждая подпрограмма может быть представлена как независимая часть графа.
Может быть показано, что цикломатическая сложность любой структурированной программы с только одной точкой входа и одной точкой выхода эквивалентна числу точек ветвления (то есть, операторов if или условных циклов), содержащихся в этой программе, плюс один.
Цикломатическая сложность может быть распространена на программу с многочисленными точками выхода; в этом случае она равна
π − s + 2,
где:
π — число точек ветвления в программе,
s — число точек выхода.
Формально, цикломатическая сложность может быть определена как относительное число Бетти:
то есть «первая гомология графа G относительно терминальных узлов t. Это другой способ сказать «число линейно независимых маршрутов через граф от входа к выходу».
Кроме того, цикломатическую сложность можно вычислить через абсолютное число Бетти (с помощью абсолютной гомологии, а не относительной), объединив все терминальные узлы данного компонента (что эквивалентно соединению точек выхода с точкой входа), в этом случае для нового, расширенного, графа
Цикломатическим числом графа называется число, равное увеличенной на единицу разности между числом ребер и числом вершин графа:
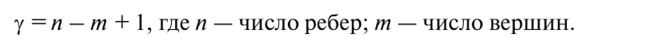
Цикломатическое число графа показывает, сколько ребер надо удалить из графа, чтобы в нем не осталось ни одного цикла.
Задача 1. Дан граф, у которого т = 6, п = 9 (рис. 8.18, а). Определить, сколько ребер на графе нужно удалить, чтобы в нем не осталось ни одого цикла.
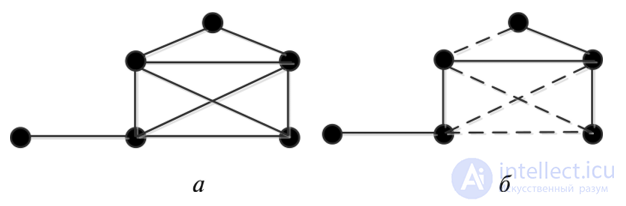
Рис. 8.18. Исходный граф (о) и остовный подграф (б)
(-------) удаленные ребра
Для заданного графа цикломатическое число у = 9 — 6 + 1 = 4. Это означает, что если на графе удалить 4 ребра, то в нем не останется ни одного цикла. Тогда остовный подграф будет иметь вид, показанный на рис. 8.18, б.
Задача 2. Какое минимальное число дверей нужно предусмотреть в замке (рис. 8.19), чтобы попасть во все комнаты (дверь — одно ребро).
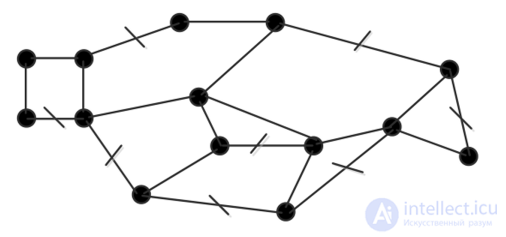
Рис. 8.19. Схема замка (вид сверху)
Решение. Число вершин т = 14, число ребер п = 21. Цикломатическое число у = 21 — 14+1 = 8. Следовательно, в замке нужно предусмотреть 8 дверей. Наряду с цикломатическим числом в теории графов вводится понятие коцикломатического числа. Пусть в графе т — число ребер, п — число вершин, р — число компонент связности. Величина г = п—р называется коцикломатическим числом (число ребер в остовах всехр связных компонент графа).
Одно из первоначально предложенных Маккейбом применений состоит в том, что необходимо ограничивать сложность программ во время их разработки. Он рекомендует, чтобы программистов обязывали вычислять сложность разрабатываемых ими модулей и разделять модули на более мелкие всякий раз, когда цикломатическая сложность этих модулей превысит десять. Эта практика была включена НИСТ-ом в методику структурного тестирования с замечанием, что со времени исходной публикации Маккейба выбор значения 10 получил весомые подтверждения, однако в некоторых случаях может быть целесообразно ослабить ограничение и разрешить модули со сложностью до 15. В данной методике признается, что иногда могут существовать причины для выхода за рамки согласованного лимита. Это сформулировано как рекомендация: «Для каждого модуля следует либо ограничивать цикломатическую сложность до согласованных пределов, либо предоставить письменное объяснение того, почему лимит был превышен».
Другое применение цикломатической сложности — определение количества тестов, необходимых для полного покрытия кода.
Он полезен, поскольку цикломатическая сложность M имеет два свойства, для конкретного модуля:
Цикломатическая сложность используется в качестве одного из параметров в индексе удобства сопровождения (англ. maintainability index) .
Исследование, описанное в статье про цикломатическая сложность, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое цикломатическая сложность, цикломатическое число и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Качество и тестирование программного обеспечения. Quality Assurance.
Из статьи мы узнали кратко, но содержательно про цикломатическая сложность
Комментарии
Оставить комментарий
Качество и тестирование программного обеспечения. Quality Assurance.
Термины: Качество и тестирование программного обеспечения. Quality Assurance.