Статистическая модель Миллса -оценка количества ошибок в программном коде, кратко

Привет, Вы узнаете о том , что такое статистическая модель миллса -оценка количества ошибок в программном коде , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое статистическая модель миллса -оценка количества ошибок в программном коде , настоятельно рекомендую прочитать все из категории Качество и тестирование программного обеспечения. Quality Assurance..

Модель Миллса — способ оценки количества ошибок в программном коде, созданный в 1972 году программистом Харланом Миллсом. Он получил широкое распространение благодаря своей простоте и интуитивной привлекательности .

Методология

Допустим, имеется программный код, в котором присутствует заранее неизвестное количество ошибок (багов), требующее максимально точной оценки. Для получения этой величины можно внести в программный код дополнительных ошибок, о наличии которых ничего не известно специалистам по тестированию[3][1].

Предположим, что после проведения тестирования было обнаружено n естественных ошибок (где n[1][4].

Из которого следует, что оценка полного количества естественных ошибок в коде равна, а количество все еще не выловленных багов кода равно разности [1][5]. Сам Миллс полагал, что процесс тестирования необходимо сопровождать постоянным обновлением графиков для оценки количества ошибок[6].

Очевидно, что такой подход не лишен недостатков. Например, если найдено 100% искусственных ошибок, то значит и естественных ошибок было найдено около 100%. Причем, чем меньше было внесено искусственных ошибок, тем больше вероятность того, что все они будут обнаружены. Из чего следует заведомо абсурдное следствие: если была внесена всего одна ошибка, которая была обнаружена при тестировании, значит ошибок в коде больше нет[6].

В целях количественной оценки доверия модели был введен следующий эмпирический критерий:

Уровень значимости оценивает вероятность, с которой модель будет правильно отклонять ложное предположение[7][6]. Выражение для было сконструировано Миллсом[7], но в силу своей эмпирической природы при необходимости оно допускает некоторую вариативность в разумных пределах[8].

Исходя из формулы для можно получить оценку количества искусственно вносимых багов для достижения нужной меры доверия . Это количество дается выражением вида [8].

Слабостью подхода Миллса является необходимость вести тестирование продукта до обнаружения абсолютно всех искусственно введенных багов, однако существуют обобщения этой модели, где это ограничение снято[7]. Например, если порог на допустимое количество из обнаруженных внесенных ошибок равен величине ), то критерий перезаписывается следующим образом:

Статистическая модель Миллса позволяет оценить не только количество ошибок до начала тестирования, но и степень отлаженности программ. Об этом говорит сайт https://intellect.icu . Для применения модели до начала тестирования в программу преднамеренно вносят ошибки. Далее считают, что обнаружение преднамеренно внесенных и так называемых собственных ошибок программы равновероятно.

Для оценки количества ошибок в программе до начала тестирования используется выражение

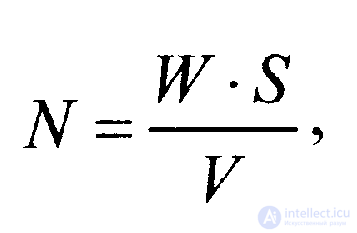(2.2.1)

где W' — количество преднамеренно внесенных в программу ошибок до начала тестирования;V— количество обнаруженных в процессе тестирования ошибок из числа преднамеренно внесенных;S— количество «собственных» ошибок программы, обнаруженных в процессе тестирования.

Если продолжать тестирование до тех пор, пока все ошибки из числа преднамеренно внесенных не будут обнаружены, степень отлаженности программы С можно оценить с помощью выражения

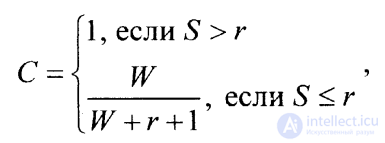(2.2.2)

где SиW=V(равенство значенийWиVв данном случае имеет место, поскольку считается, что все преднамеренно внесенные ошибки обнаружены) имеют тот же смысл, что и в предыдущем выражении (2.2.1), аr означает верхний предел (максимум) предполагаемого количества «собственных» ошибок в программе.

Выражения (2.2.1) и (2.2.2) представляют собой статистическую модель Миллса. Необходимо заметить, что если тестирование будет закончено преждевременно (т. е. раньше, чем будут обнаружены все преднамеренно внесенные ошибки), то вместо выражения (2.2.2) следует использовать более сложное комбинаторное выражение (2.2.3). Если обнаружено только Vошибок изWпреднамеренно внесенных, используется выражение

!!!(2.2.3)

где в круглых скобках записаны обозначения для числа сочетаний из Sэлементов поV— 1 элементов в каждой комбинации и числа сочетаний изS+r+ 1 элементов поr+Vэлементов в каждой комбинации.

2.2.2. Задачи по применению модели Миллса

Задача 1

В программу преднамеренно внесли (посеяли) 10 ошибок. В результате тестирования обнаружено 12 ошибок, из которых 10 ошибок были внесены преднамеренно. Все обнаруженные ошибки исправлены. До начала тестирования предполагалось, что программа содержит не более 4 ошибок. Требуется оценить количество ошибок до начала тестирования и степень отлаженности программы.

Решение задачи

Для оценки количества ошибок до начала тестирования используем формулу (2.2.1).

Нам известно:

• количество внесенных в программу ошибок W= 10;

• количество обнаруженных ошибок из числа внесенных V= 10;

• количество «собственных» ошибок в программе S= 12 — 10 = 2.

Подставив указанные значения в формулу, получим оценку количества ошибок:

N = (W·S) /V= (10 ·2) / 10 = 2.

Таким образом, из результатов тестирования следует, что до начала тестирования в программе имелось 2 ошибки.

Для оценки отлаженности программы используем уравнение (2.2.2). Нам известно:

• количество обнаруженных «собственных» ошибок в программе S=2;

• количество предполагаемых ошибок в программе r= 4;

• количество преднамеренно внесенных и обнаруженных ошибок W= 10.

Очевидно, что обнаружено меньшее число «собственных» ошибок, чем количество предполагаемых ошибок в программе (S<r). Для оценки отлаженности программы используем уравнение

С =W/ (W +r + 1) = 10/ (10 + 4 + 1) = 0,67.

Степень отлаженности программы равна 0,67, что составляет 67%.

Задача 2

В программу было преднамеренно внесено (посеяно) 14 ошибок. Предположим, что в программе перед началом тестирования было 14 ошибок. В процессе четырех тестовых прогонов было выявлено следующее количество ошибок.

Необходимо оценить количество ошибок перед каждым тестовым прогоном. Оценить степень отлаженности программы после последнего прогона. Построить диаграмму зависимости возможного числа ошибок в данной программе от номера тестового прогона.

Решение задачи

Количество ошибок перед каждым прогоном будем оценивать в соответствии с выражением (2.2.1). Перед каждой последующей оценкой количества ошибок и степени отлаженности программы необходимо корректировать значения внесенных Wи предполагаемыхr ошибок с учетом выявленных и устраненных после каждого прогона тестов. Степень отлаженности программы на всех прогонах, кроме последнего (2.2.2), рассчитывается по комбинаторной формуле (2.2.3).

Определяя показатели программы по результатам первого прогона, необходимо учитывать, что W1= 14;S1= 4;V1= 6, тогда

N1= (W1 · S1) /V1= (14·4) / 6 = 9.

Перед вторым прогоном корректируем исходные данные для оценки параметров: r2= 14 — 4 = 10;W2= 14 — 6 = 8;S2= 2;V2= 4, тогда

N2= (W2 · S2) /V2= (8·2) / 4 = 4.

Корректировка исходных данных перед третьим прогоном дает следующие данные. r3 = 10 — 2 = 8,W3= 8 — 4 = 4;S3= 1;V3= 2, откуда количество ошибок определится следующим образом:

N3= (W3 · S3) /V3= (4 · 1) / 2 = 2.

Перед четвертым прогоном программы получим следующие исходные данные: r4 = 8 — 1 = 7,W4= 4 — 2 = 2;S4= 1;V4= 2, тогда

N4= (W4 · S4) /V4= (2 ·1) /2 = 1.

Поскольку после четвертого прогона все «посеянные» ошибки выявлены и устранены, то для оценки отлаженности программы можно воспользоваться упрощенной формулой

С=W/(W+r+ 1) =2/(2+ 7+ 1) =0,2.

Таким образом, в предположении, что до начала четвертого прогона в программе оставалось 7 ошибок, степень отлаженности программы составляет 20%.

Результат по количеству ошибок в программе до начала каждого прогона приведен ниже.

Анализ данных, представленных в статье про статистическая модель миллса -оценка количества ошибок в программном коде , подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое статистическая модель миллса -оценка количества ошибок в программном коде и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Качество и тестирование программного обеспечения. Quality Assurance.