Лекция
Сразу хочу сказать, что здесь никакой воды про обучение с учителем, и только нужная информация. Для того чтобы лучше понимать что такое обучение с учителем, метод коррекции ошибки, метод обратного распространения ошибки , настоятельно рекомендую прочитать все из категории Машинное обучение.
обучение с учителем (англ. Supervised learning) — один из способов машинного обучения, в ходе которого испытуемая система принудительно обучается с помощью примеров «стимул-реакция». С точки зрения кибернетики, является одним из видов кибернетического эксперимента. Между входами и эталонными выходами (стимул-реакция) может существовать некоторая зависимость, но она не известна. Известна только конечная совокупность прецедентов — пар «стимул-реакция», называемая обучающей выборкой. На основе этих данных требуется восстановить зависимость (построить модель отношений стимул-реакция, пригодных для прогнозирования), то есть построить алгоритм, способный для любого объекта выдать достаточно точный ответ. Для измерения точности ответов, так же как и в обучении на примерах, может вводиться функционал качества.
Данный эксперимент представляет собой частный случай кибернетического эксперимента с обратной связью. Постановка данного эксперимента предполагает наличие экспериментальной системы, метода обучения и метода испытания системы или измерения характеристик.
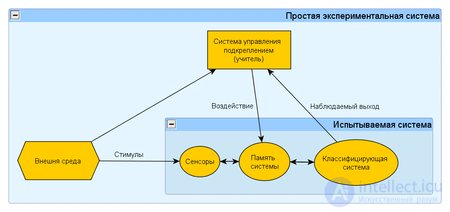
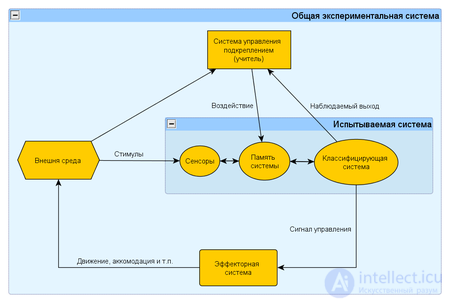
Экспериментальная система в свою очередь состоит из испытываемой (используемой) системы, пространства стимулов получаемых из внешней среды и системы управления подкреплением (регулятора внутренних параметров). В качестве системы управления подкреплением может быть использовано автоматическое регулирующие устройство (например, термостат) или человек-оператор (учитель), способный реагировать на реакции испытываемой системы и стимулы внешней среды путем применения особых правил подкрепления, изменяющих состояние памяти системы.
Различают два варианта: (1) когда реакция испытываемой системы не изменяет состояние внешней среды, и (2) когда реакция системы изменяет стимулы внешней среды. Эти схемы указывают принципиальное сходство такой системы общего вида с биологической нервной системой.
Данное различие позволяет более глубоко взглянуть на различия между различными способами обучения, так как грань между обучением с учителем и обучением без учителя более тонка. Кроме этого, такое различие позволило показать дляискусственных нейронных сетей определенные ограничения для S и R — управляемых систем (см. Теорема сходимости перцептрона).
Обучение с учителем (supervised learning) предполагает наличие полного набора размеченных данных для тренировки модели на всех этапах ее построения.
Наличие полностью размеченного датасета означает, что каждому примеру в обучающем наборе соответствует ответ, который алгоритм и должен получить. Таким образом, размеченный датасет из фотографий цветов обучит нейронную сеть, где изображены розы, ромашки или нарциссы. Когда сеть получит новое фото, она сравнит его с примерами из обучающего датасета, чтобы предсказать ответ.
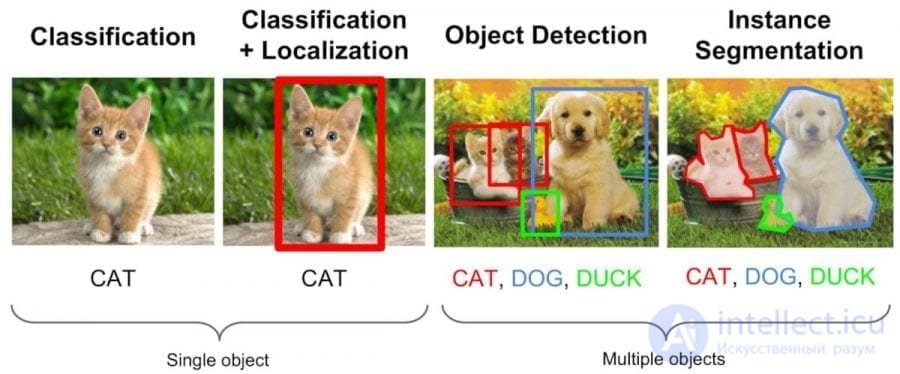
Пример обучения с учителем — классификация (слева), и дальнейшее ее использование для сегментации и распознавания объектов
В основном обучение с учителем применяется для решения двух типов задач: классификации и регрессии.
В задачах классификации алгоритм предсказывает дискретные значения, соответствующие номерам классов, к которым принадлежат объекты. В обучающем датасете с фотографиями животных каждое изображение будет иметь соответствующую метку — «кошка», «коала» или «черепаха». Качество алгоритма оценивается тем, насколько точно он может правильно классифицировать новые фото с коалами и черепахами.
А вот задачи регрессии связаны с непрерывными данными. Один из примеров, линейная регрессия, вычисляет ожидаемое значение переменной y, учитывая конкретные значения x.
Более утилитарные задачи машинного обучения задействуют большое число переменных. Как пример, нейронная сеть, предсказывающая цену квартиры в Сан-Франциско на основе ее площади, местоположения и доступности общественного транспорта. Алгоритм выполняет работу эксперта, который рассчитывает цену квартиры исходя из тех же данных.
Таким образом, обучение с учителем больше всего подходит для задач, когда имеется внушительный набор достоверных данных для обучения алгоритма. Но так бывает далеко не всегда. Недостаток данных — наиболее часто встречающаяся проблема в машинном обучении .
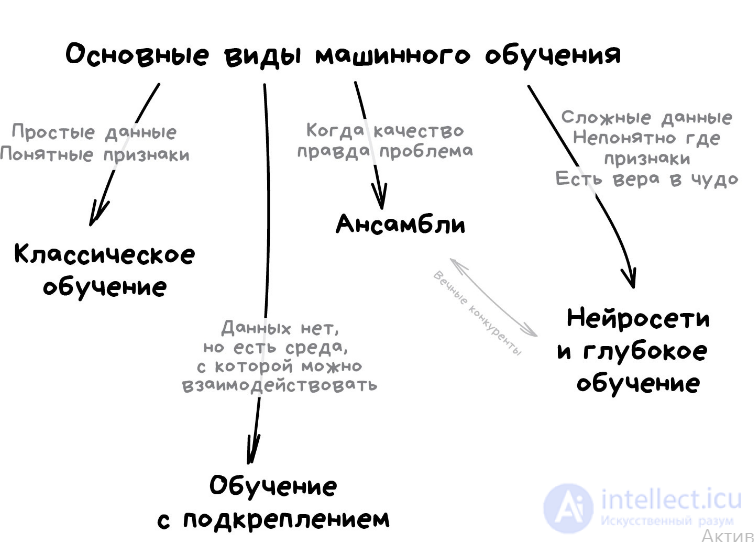
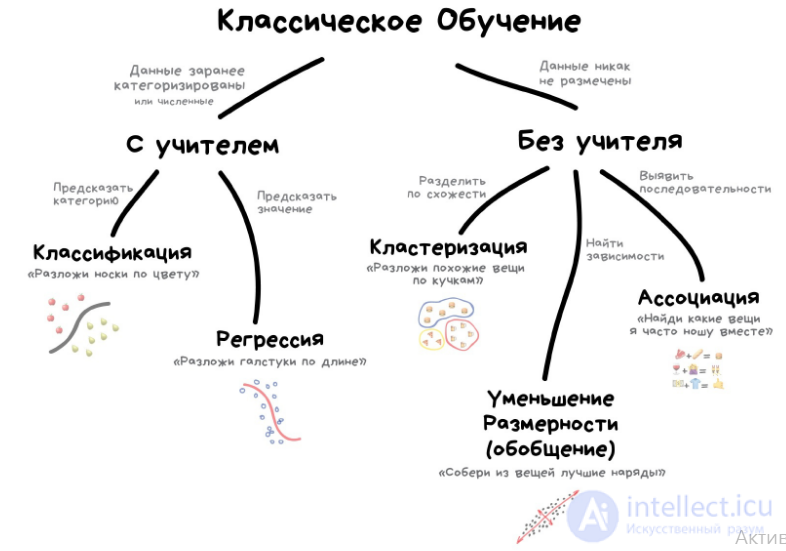
Классическое обучение любят делить на две категории — с учителем и без. Часто можно встретить их английские наименования — Supervised и Unsupervised Learning.
В первом случае у машины есть некий учитель, который говорит ей как правильно. Рассказывает, что на этой картинке кошка, а на этой собака. То есть учитель уже заранее разделил (разметил) все данные на кошек и собак, а машина учится на конкретных примерах.
В обучении без учителя, машине просто вываливают кучу фотографий животных на стол и говорят «разберись, кто здесь на кого похож». Данные не размечены, у машины нет учителя, и она пытается сама найти любые закономерности. Об этих методах поговорим ниже.
Очевидно, что с учителем машина обучится быстрее и точнее, потому в боевых задачах его используют намного чаще. Эти задачи делятся на два типа: классификация — предсказание категории объекта, и регрессия — предсказание места на числовой прямой.
4 комментария
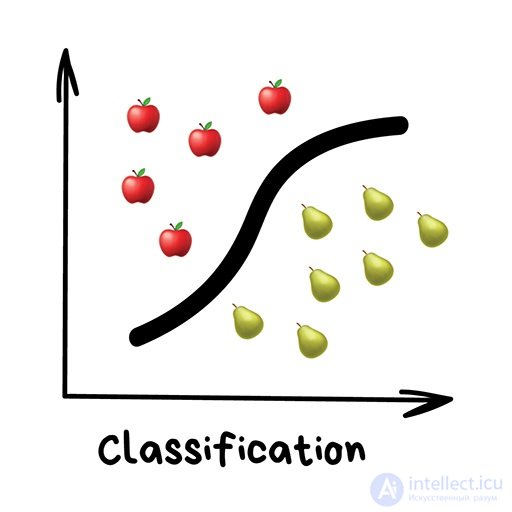
«Разделяет объекты по заранее известному признаку. Носки по цветам, документы по языкам, музыку по жанрам»
Сегодня используют для:
Популярные алгоритмы: Наивный Байес, Деревья Решений, Логистическая Регрессия, K-ближайших соседей, Машины Опорных Векторов
Здесь и далее в комментах можно дополнять эти блоки. Приводите свои примеры задач, областей и алгоритмов, потому что описанные мной взяты из субъективного опыта.
6 комментариев
Классификация вещей — самая популярная задача во всем машинном обучении. Машина в ней как ребенок, который учится раскладывать игрушки: роботов в один ящик, танки в другой. Опа, а если это робот-танк? Штош, время расплакаться и выпасть в ошибку.
Старый доклад Бобука про повышение конверсии лендингов с помощью SVM
Для классификации всегда нужен учитель — размеченные данные с признаками и категориями, которые машина будет учиться определять по этим признакам. Дальше классифицировать можно что угодно: пользователей по интересам — так делают алгоритмические ленты, статьи по языкам и тематикам — важно для поисковиков, музыку по жанрам — вспомните плейлисты Спотифая и Яндекс.Музыки, даже письма в вашем почтовом ящике.
Раньше все спам-фильтры работали на алгоритме Наивного Байеса. Машина считала сколько раз слово «виагра» встречается в спаме, а сколько раз в нормальных письмах. Перемножала эти две вероятности по формуле Байеса, складывала результаты всех слов и бац, всем лежать, у нас машинное обучение!
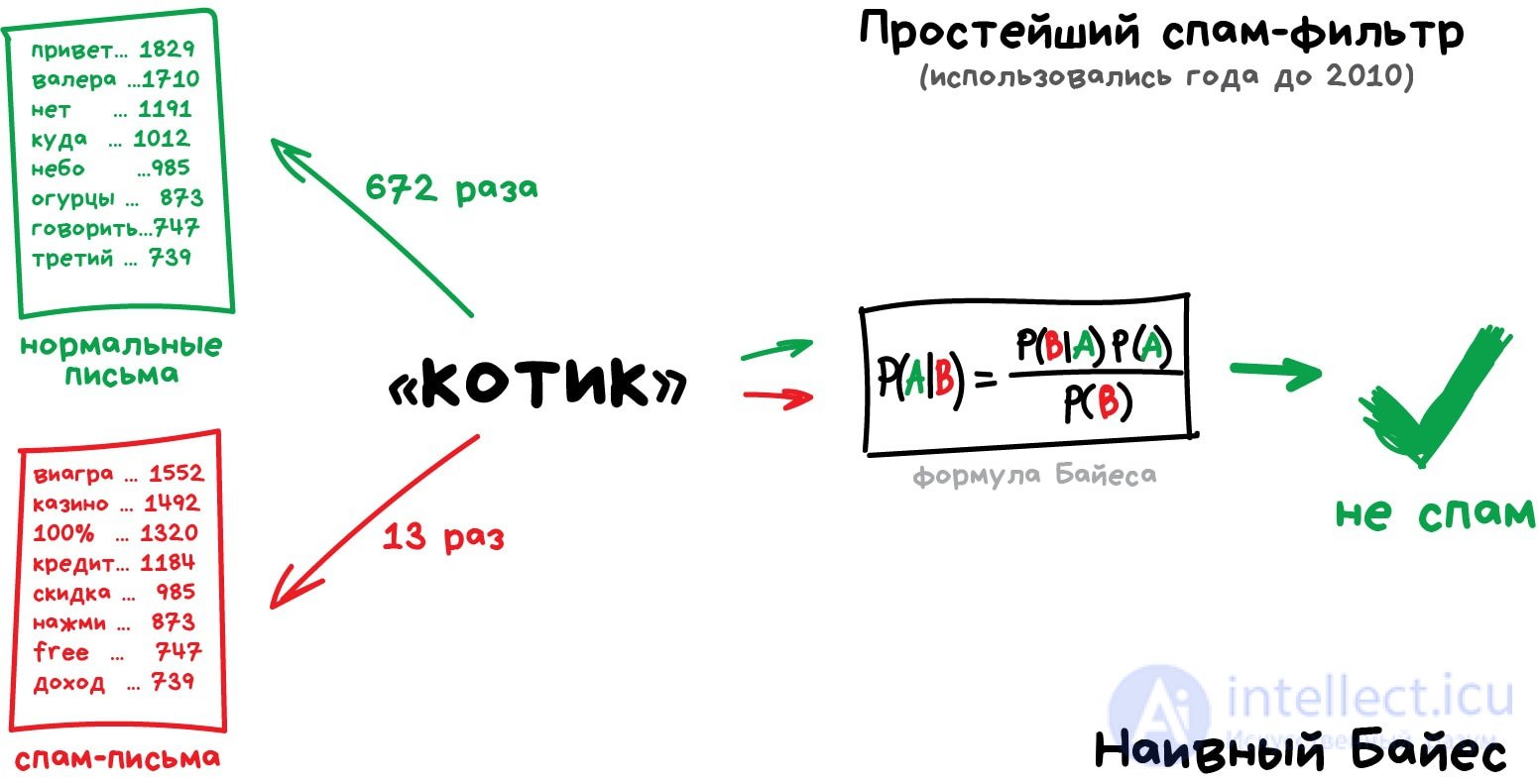
Позже спамеры научились обходить фильтр Байеса, просто вставляя в конец письма много слов с «хорошими» рейтингами. Метод получил ироничное название Отравление Байеса, а фильтровать спам стали другими алгоритмами. Но метод навсегда остался в учебниках как самый простой, красивый и один из первых практически полезных.
Возьмем другой пример полезной классификации. Вот берете вы кредит в банке. Об этом говорит сайт https://intellect.icu . Как банку удостовериться, вернете вы его или нет? Точно никак, но у банка есть тысячи профилей других людей, которые уже брали кредит до вас. Там указан их возраст, образование, должность, уровень зарплаты и главное — кто из них вернул кредит, а с кем возникли проблемы.
Да, все догадались, где здесь данные и какой надо предсказать результат. Обучим машину, найдем закономерности, получим ответ — вопрос не в этом. Проблема в том, что банк не может слепо доверять ответу машины, без объяснений. Вдруг сбой, злые хакеры или бухой админ решил скриптик исправить.
Для этой задачи придумали Деревья Решений. Машина автоматически разделяет все данные по вопросам, ответы на которые «да» или «нет». Вопросы могут быть не совсем адекватными с точки зрения человека, например «зарплата заемщика больше, чем 25934 рубля?», но машина придумывает их так, чтобы на каждом шаге разбиение было самым точным.
Так получается дерево вопросов. Чем выше уровень, тем более общий вопрос. Потом даже можно загнать их аналитикам, и они навыдумывают почему так.
Деревья нашли свою нишу в областях с высокой ответственностью: диагностике, медицине, финансах.
Два самых популярных алгоритма построения деревьев — CART и C4.5.
В чистом виде деревья сегодня используют редко, но вот их ансамбли (о которых будет ниже) лежат в основе крупных систем и зачастую уделывают даже нейросети. Например, когда вы задаете вопрос Яндексу, именно толпа глупых деревьев бежит ранжировать вам результаты.

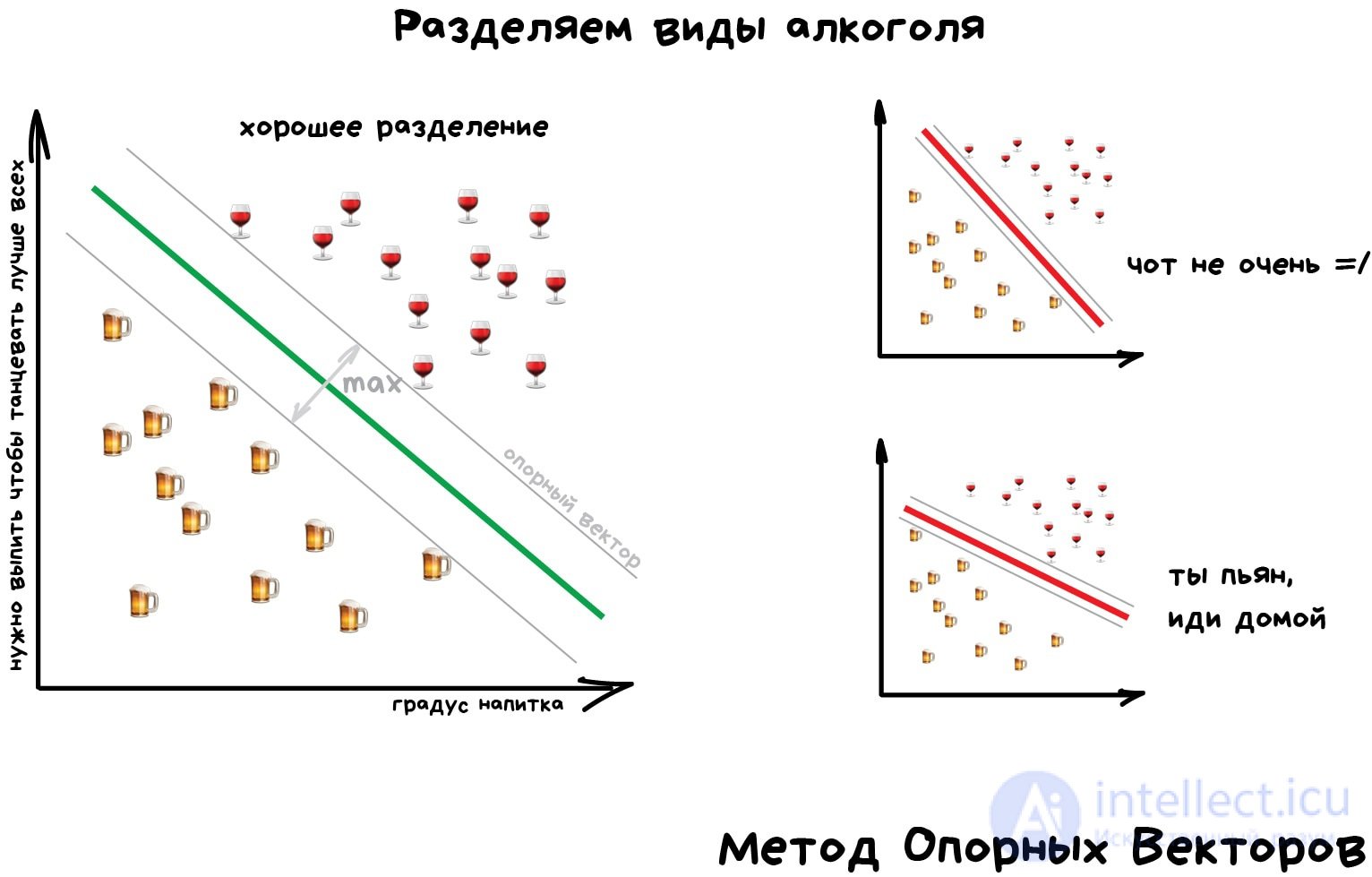
Но самым популярным методом классической классификации заслуженно является Метод Опорных Векторов (SVM). Им классифицировали уже все: виды растений, лица на фотографиях, документы по тематикам, даже странных Playboy-моделей. Много лет он был главным ответом на вопрос «какой бы мне взять классификатор».
Идея SVM по своей сути проста — он ищет, как так провести две прямые между категориями, чтобы между ними образовался наибольший зазор. На картинке видно нагляднее:
У классификации есть полезная обратная сторона — поиск аномалий. Когда какой-то признак объекта сильно не вписывается в наши классы, мы ярко подсвечиваем его на экране. Сейчас так делают в медицине: компьютер подсвечивает врачу все подозрительные области МРТ или выделяет отклонения в анализах. На биржах таким же образом определяют нестандартных игроков, которые скорее всего являются инсайдерами. Научив компьютер «как правильно», мы автоматически получаем и обратный классификатор — как неправильно.
Сегодня для классификации все чаще используют нейросети, ведь по сути их для этого и изобрели.
Правило буравчика такое: сложнее данные — сложнее алгоритм. Для текста, цифр, табличек я бы начинал с классики. Там модели меньше, обучаются быстрее и работают понятнее. Для картинок, видео и другой непонятной бигдаты — сразу смотрел бы в сторону нейросетей.
Лет пять назад еще можно было встретить классификатор лиц на SVM, но сегодня под эту задачу сотня готовых сеток по интернету валяются, чо бы их не взять. А вот спам-фильтры как на SVM писали, так и не вижу смысла останавливаться.
«Нарисуй линию вдоль моих точек. Да, это машинное обучение»
Сегодня используют для:
Популярные алгоритмы: Линейная или Полиномиальная Регрессия
Регрессия — та же классификация, только вместо категории мы предсказываем число. Стоимость автомобиля по его пробегу, количество пробок по времени суток, объем спроса на товар от роста компании и.т.д. На регрессию идеально ложатся любые задачи, где есть зависимость от времени.
Регрессию очень любят финансисты и аналитики, она встроена даже в Excel. Внутри все работает, опять же, банально: машина тупо пытается нарисовать линию, которая в среднем отражает зависимость. Правда, в отличии от человека с фломастером и вайтбордом, делает она это математически точно — считая среднее расстояние до каждой точки и пытаясь всем угодить.

Когда регрессия рисует прямую линию, ее называют линейной, когда кривую — полиномиальной. Это два основных вида регрессии, дальше уже начинаются редкоземельные методы. Но так как в семье не без урода, есть Логистическая Регрессия, которая на самом деле не регрессия, а метод классификации, от чего у всех постоянно путаница. Не делайте так.
Схожесть регрессии и классификации подтверждается еще и тем, что многие классификаторы, после небольшого тюнинга, превращаются в регрессоры. Например, мы можем не просто смотреть к какому классу принадлежит объект, а запоминать, насколько он близок — и вот, у нас регрессия.
Для желающих понять это глубже, но тоже простыми словами, рекомендую цикл статей Machine Learning for Humans
Эта статья о нейросетях; о коррекции ошибок в информатике см.: обнаружение и исправление ошибок.
Метод коррекции ошибки — метод обучения перцептрона, предложенный Фрэнком Розенблаттом. Представляет собой такой метод обучения, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.
В теореме сходимости перцептрона различаются различные виды этого метода, доказано, что любой из них позволяет получить схождение при решении любой задачи классификации.
Если реакция на стимул 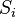 правильная, то никакого подкрепления не вводится, но при появлении ошибок к весу каждого активного А-элемента прибавляется величина
правильная, то никакого подкрепления не вводится, но при появлении ошибок к весу каждого активного А-элемента прибавляется величина 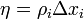 , где
, где 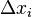 — число единиц подкрепления, выбирается так, чтобы величина сигнала превышала порог θ, а
— число единиц подкрепления, выбирается так, чтобы величина сигнала превышала порог θ, а 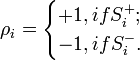 , при этом
, при этом 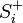 — стимул, принадлежащий положительному классу, а
— стимул, принадлежащий положительному классу, а 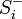 — стимул, принадлежащий отрицательному классу.
— стимул, принадлежащий отрицательному классу.
Отличается от метода коррекции ошибок без квантования только тем, что 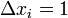 , то есть равно одной единице подкрепления.
, то есть равно одной единице подкрепления.
Этот метод и метод коррекции ошибок без квантованиея являются одинаковыми по скорости достижения решения в общем случае, и более эффективными по сравнению с методами коррекции ошибок со случайным знаком или случайными возмущениями.
Отличается тем, что знак подкрепления 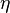 выбирается случайно независимо от реакции перцептрона и с равной вероятностью может быть положительным или отрицательным. Но так же как и в базовом методе — если перцептрон дает правильную реакцию, то подкрепление равно нулю.
выбирается случайно независимо от реакции перцептрона и с равной вероятностью может быть положительным или отрицательным. Но так же как и в базовом методе — если перцептрон дает правильную реакцию, то подкрепление равно нулю.
Отличается тем, что величина и знак 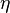 для каждой связи в системе выбираются отдельно и независимо в соответствии с некоторым распределением вероятностей. Это метод приводит к самой медленной сходимости, по сравнению с выше описанными модификациями.
для каждой связи в системе выбираются отдельно и независимо в соответствии с некоторым распределением вероятностей. Это метод приводит к самой медленной сходимости, по сравнению с выше описанными модификациями.
Метод обратного распространения ошибки (англ. backpropagation)— метод обучения многослойного перцептрона. Впервые метод был описан в 1974 г. А.И. Галушкиным , а также независимо и одновременно Полом Дж. Вербосом . Далее существенно развит в 1986 г. Дэвидом И. Румельхартом, Дж. Е. Хинтоном и Рональдом Дж. Вильямсом и независимо и одновременно С.И. Барцевым и В.А. Охониным (Красноярская группа) .. Это итеративный градиентный алгоритм, который используется с целью минимизации ошибки работы многослойного перцептрона и получения желаемого выхода.
Основная идея этого метода состоит в распространении сигналов ошибки от выходов сети к ее входам, в направлении, обратном прямому распространению сигналов в обычном режиме работы. Барцев и Охонин предложили сразу общий метод («принцип двойственности»), приложимый к более широкому классу систем, включая системы с запаздыванием, распределенные системы, и т. п.
Для возможности применения метода обратного распространения ошибки передаточная функция нейронов должна быть дифференцируема. Метод является модификацией классического метода градиентного спуска.
Наиболее часто в качестве функций активации используются следующие виды сигмоид:
Функция Ферми (экспоненциальная сигмоида):

Рациональная сигмоида:
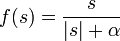
Гиперболический тангенс:
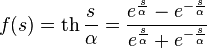 ,
,
где s — выход сумматора нейрона,  — произвольная константа.
— произвольная константа.
Менее всего, сравнительно с другими сигмоидами, процессорного времени требует расчет рациональной сигмоиды. Для вычисления гиперболического тангенса требуется больше всего тактов работы процессора. Если же сравнивать с пороговыми функциями активации, то сигмоиды рассчитываются очень медленно. Если после суммирования в пороговой функции сразу можно начинать сравнение с определенной величиной (порогом), то в случае сигмоидальной функции активации нужно рассчитать сигмоид (затратить время в лучшем случае на три операции: взятие модуля, сложение и деление), и только потом сравнивать с пороговой величиной (например, нулем). Если считать, что все простейшие операции рассчитываются процессором за примерно одинаковое время, то работа сигмоидальной функции активации после произведенного суммирования (которое займет одинаковое время) будет медленнее пороговой функции активации как 1:4.
В тех случаях, когда удается оценить работу сети, обучение нейронных сетей можно представить как задачу оптимизации. Оценить — означает указать количественно, хорошо или плохо сеть решает поставленные ей задачи. Для этого строится функция оценки. Она, как правило, явно зависит от выходных сигналов сети и неявно (через функционирование) — от всех ее параметров. Простейший и самый распространенный пример оценки — сумма квадратов расстояний от выходных сигналов сети до их требуемых значений:
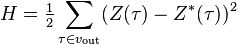 ,
,
где 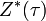 — требуемое значение выходного сигнала.
— требуемое значение выходного сигнала.
Метод наименьших квадратов далеко не всегда является лучшим выбором оценки. Тщательное конструирование функции оценки позволяет на порядок повысить эффективность обучения сети, а также получать дополнительную информацию — «уровень уверенности» сети в даваемом ответе .
Архитектура многослойного перцептрона
Алгоритм обратного распространения ошибки применяется для многослойного перцептрона. У сети есть множество входов 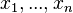 , множество выходов Outputs и множество внутренних узлов. Перенумеруем все узлы (включая входы и выходы) числами от 1 до N (сквозная нумерация, вне зависимости от топологии слоев). Обозначим через
, множество выходов Outputs и множество внутренних узлов. Перенумеруем все узлы (включая входы и выходы) числами от 1 до N (сквозная нумерация, вне зависимости от топологии слоев). Обозначим через  вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через
вес, стоящий на ребре, соединяющем i-й и j-й узлы, а через  — выход i-го узла. Если нам известен обучающий пример (правильные ответы сети
— выход i-го узла. Если нам известен обучающий пример (правильные ответы сети 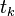 ,
, 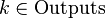 ), то функция ошибки, полученная по методу наименьших квадратов, выглядит так:
), то функция ошибки, полученная по методу наименьших квадратов, выглядит так:
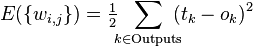
Как модифицировать веса? Мы будем реализовывать стохастический градиентный спуск, то есть будем подправлять веса после каждого обучающего примера и, таким образом, «двигаться» в многомерном пространстве весов. Чтобы «добраться» до минимума ошибки, нам нужно «двигаться» в сторону, противоположную градиенту, то есть, на основании каждой группы правильных ответов, добавлять к каждому весу 
 ,
,
где 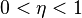 — множитель, задающий скорость «движения».
— множитель, задающий скорость «движения».
Производная считается следующим образом. Пусть сначала 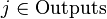 , то есть интересующий нас вес входит в нейрон последнего уровня. Сначала отметим, что
, то есть интересующий нас вес входит в нейрон последнего уровня. Сначала отметим, что  влияет на выход сети только как часть суммы
влияет на выход сети только как часть суммы 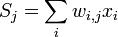 , где сумма берется по входам j-го узла. Поэтому
, где сумма берется по входам j-го узла. Поэтому
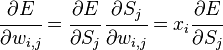
Аналогично, 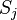 влияет на общую ошибку только в рамках выхода j-го узла
влияет на общую ошибку только в рамках выхода j-го узла 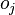 (напоминаем, что это выход всей сети). Поэтому
(напоминаем, что это выход всей сети). Поэтому
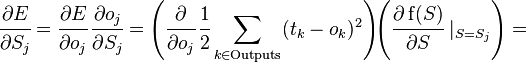
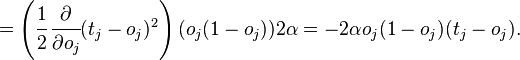
где 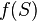 - соответствующая сигмоида, в данном случае - экспоненциальная
- соответствующая сигмоида, в данном случае - экспоненциальная

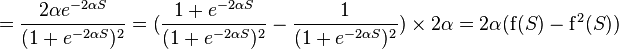
Если же j-й узел — не на последнем уровне, то у него есть выходы; обозначим их через Children(j). В этом случае
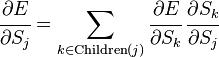 ,
,
и
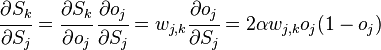 .
.
Ну а 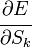 — это в точности аналогичная поправка, но вычисленная для узла следующего уровня будем обозначать ее через
— это в точности аналогичная поправка, но вычисленная для узла следующего уровня будем обозначать ее через 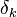 — от
— от 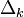 она отличается отсутствием множителя
она отличается отсутствием множителя  . Поскольку мы научились вычислять поправку для узлов последнего уровня и выражать поправку для узла более низкого уровня через поправки более высокого, можно уже писать алгоритм. Именно из-за этой особенности вычисления поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
. Поскольку мы научились вычислять поправку для узлов последнего уровня и выражать поправку для узла более низкого уровня через поправки более высокого, можно уже писать алгоритм. Именно из-за этой особенности вычисления поправок алгоритм называется алгоритмом обратного распространения ошибки (backpropagation). Краткое резюме проделанной работы:
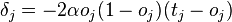
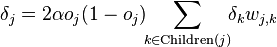

, где 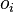 это тот же
это тот же 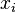 в формуле для
в формуле для 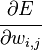
Получающийся алгоритм представлен ниже. На вход алгоритму, кроме указанных параметров, нужно также подавать в каком-нибудь формате структуру сети. На практике очень хорошие результаты показывают сети достаточно простой структуры, состоящие из двух уровней нейронов — скрытого уровня (hidden units) и нейронов-выходов (output units); каждый вход сети соединен со всеми скрытыми нейронами, а результат работы каждого скрытого нейрона подается на вход каждому из нейронов-выходов. В таком случае достаточно подавать на вход количество нейронов скрытого уровня.
Алгоритм: BackPropagation 
 маленькими случайными значениями,
маленькими случайными значениями, 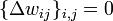
Для всех d от 1 до m:
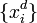 на вход сети и подсчитать выходы
на вход сети и подсчитать выходы  каждого узла.
каждого узла.
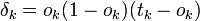 .
.
Для каждого узла j уровня l вычислить
 .
.
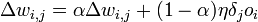 .
.
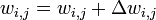 .
.
 .
.где  — коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции
— коэффициент инерциальнности для сглаживания резких скачков при перемещении по поверхности целевой функции
На каждой итерации алгоритма обратного распространения весовые коэффициенты нейронной сети модифицируются так, чтобы улучшить решение одного примера. Таким образом, в процессе обучения циклически решаются однокритериальные задачи оптимизации.
Обучение нейронной сети характеризуется четырьмя специфическими ограничениями, выделяющими обучение нейросетей из общих задач оптимизации: астрономическое число параметров, необходимость высокого параллелизма при обучении, многокритериальность решаемых задач, необходимость найти достаточно широкую область, в которой значения всех минимизируемых функций близки к минимальным. В остальном проблему обучения можно, как правило, сформулировать как задачу минимизации оценки. Осторожность предыдущей фразы («как правило») связана с тем, что на самом деле нам неизвестны и никогда не будут известны все возможные задачи для нейронных сетей, и, быть может, где-то в неизвестности есть задачи, которые несводимы к минимизации оценки. Минимизация оценки — сложная проблема: параметров астрономически много (для стандартных примеров, реализуемых на РС — от 100 до 1000000), адаптивный рельеф (график оценки как функции от подстраиваемых параметров) сложен, может содержать много локальных минимумов.
Несмотря на многочисленные успешные применения обратного распространения, оно не является панацеей. Больше всего неприятностей приносит неопределенно долгий процесс обучения. В сложных задачах для обучения сети могут потребоваться дни или даже недели, она может и вообще не обучиться. Причиной может быть одна из описанных ниже.
В процессе обучения сети значения весов могут в результате коррекции стать очень большими величинами. Это может привести к тому, что все или большинство нейронов будут функционировать при очень больших значениях OUT, в области, где производная сжимающей функции очень мала. Так как посылаемая обратно в процессе обучения ошибка пропорциональна этой производной, то процесс обучения может практически замереть. В теоретическом отношении эта проблема плохо изучена. Обычно этого избегают уменьшением размера шага η, но это увеличивает время обучения. Различные эвристики использовались для предохранения от паралича или для восстановления после него, но пока что они могут рассматриваться лишь как экспериментальные.
Обратное распространение использует разновидность градиентного спуска, то есть осуществляет спуск вниз по поверхности ошибки, непрерывно подстраивая веса в направлении к минимуму. Поверхность ошибки сложной сети сильно изрезана и состоит из холмов, долин, складок и оврагов в пространстве высокой размерности. Сеть может попасть в локальный минимум (неглубокую долину), когда рядом имеется гораздо более глубокий минимум. В точке локального минимума все направления ведут вверх, и сеть неспособна из него выбраться. Основную трудность при обучении нейронных сетей составляют как раз методы выхода из локальных минимумов: каждый раз выходя из локального минимума снова ищется следующий локальный минимум тем же методом обратного распространения ошибки до тех пор, пока найти из него выход уже не удается.
Внимательный разбор доказательства сходимости показывает, что коррекции весов предполагаются бесконечно малыми. Ясно, что это неосуществимо на практике, так как ведет к бесконечному времени обучения. Размер шага должен браться конечным. Если размер шага фиксирован и очень мал, то сходимость слишком медленная, если же он фиксирован и слишком велик, то может возникнуть паралич или постоянная неустойчивость. Эффективно увеличивать шаг до тех пор, пока не прекратится улучшение оценки в данном направлении антиградиента и уменьшать, если такого улучшения не происходит. П. Д. Вассерман описал адаптивный алгоритм выбора шага, автоматически корректирующий размер шага в процессе обучения. В книге А. Н. Горбаня предложена разветвленная технология оптимизации обучения.
Следует также отметить возможность переобучения сети, что является скорее результатом ошибочного проектирования ее топологии. При слишком большом количестве нейронов теряется свойство сети обобщать информацию. Весь набор образов, предоставленных к обучению, будет выучен сетью, но любые другие образы, даже очень похожие, могут быть классифицированы неверно.
А как ты думаешь, при улучшении обучение с учителем, будет лучше нам? Надеюсь, что теперь ты понял что такое обучение с учителем, метод коррекции ошибки, метод обратного распространения ошибки и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Машинное обучение
Термины: Машинное обучение