Лекция
Сразу хочу сказать, что здесь никакой воды про машинное обучение на больших данных , и только нужная информация. Для того чтобы лучше понимать что такое машинное обучение на больших данных , машинное обучение, большие данные , настоятельно рекомендую прочитать все из категории Машинное обучение.
Не так давно получил распространение термин « большие данные », обозначивший новую прикладную область — поиск способов автоматического быстрого анализа огромных объемов разнородной информации. Наука о больших данных еще только оформляется, но уже сейчас она очень востребована — и в будущем будет востребована только больше.
С ее помощью можно решать невероятные задачи: оценивать состояние печени по кардиограмме, предсказывать зарплату по описанию вакансии, предлагать пользователю музыку на основании его анкеты в интернете. Большими данными может оказаться что угодно: результаты научных экспериментов, логи банковских транзакций, метеорологические наблюдения, профили в социальных сетях — словом, все, что может быть полезно проанализировать. Самым перспективным подходом к анализу больших данных считается применение машинного обучения — набора методов, благодаря которым компьютер может находить в массивах изначально неизвестные взаимосвязи и закономерности.
Краткая программа курса:
1. Введение. Примеры задач. Логические методы: решающие деревья и решающие леса.
2. Метрические методы классификации. Линейные методы, стохастический градиент.
3. Метод опорных векторов (SVM). Логистическая регрессия. Метрики качества классификации.
4. Линейная регрессия. Понижение размерности, метод главных компонент.
5. Композиции алгоритмов, градиентный бустинг. Нейронные сети.
6. Кластеризация и визуализация. Частичное обучение.
7. Прикладные задачи анализа данных: постановки и методы решения.
Слушателю нужно знать об основных понятиях математики: функциях, производных, векторах, матрицах. Для выполнения практических заданий потребуются базовые навыки программирования. Очень желательно знать Python
§1 Первый отборочный этап
1.1. Задачи по математике
1.2. Задачи по информатике
§2 Второй отборочный эта
2.1. Задачи по анализу данных
§3 Заключительный этап: индивидуальная часть
3.1. Задачи по математике
3.2. Задачи по информатике
§4 Заключительный этап: командная часть
4.1. Описание исходных данных
4.1.1. Граф пользователей
4.1.2. Демография пользователей
4.2 Формулировки задач
Задача 4.2.1 «Дата рождения»
Задача 4.2.2 «Регион»
Задача 4.2.3 «Поиск связей»
Задача 1.1.1 (1 балл)
В поисках внеземной жизни ученые обнаружили интересный живой организм -
Камкохоб. Эксперименты в земных условиях показали, что Камкохоб размножается
делением. То есть родительский организм исчезает, и образуются новые особи. При этом
каждая особь либо делится ровно на 5 потомков, либо не размножается, а остается одной
особью . Экспериментальный образец, привезенный на Землю размножался, некоторые его
потомки тоже размножались. Выберите в таблице, какое количество потомков могло
получиться в итоге, а какое не могло.

РЕШЕНИЕ:
Правильный ответ на поставленную задачу представлен в таблице. Подробнее ход
решения рассматривается в следующей задаче.

Задача 1.1.2 (1 балл)
В поисках внеземной жизни ученые обнаружили интересный живой организм -
Камкохоб. Эксперименты в земных условиях показали, что Камкохоб размножается
делением. То есть родительский организм исчезает, и образуются новые особи. При этом
каждая особь либо делится ровно на 5 потомков, либо не размножается, а остается одной
особью. Экспериментальный образец, привезенный на Землю, размножался, некоторые его
потомки тоже размножались. Какое количество потомков могло получиться? Опишите всю
серию возможных ответов общей формулой, используя переменную x (где х - натуральное
число).
РЕШЕНИЕ:
Посмотрим, как меняется общее количество особей при одном размножении.
Родительская особь исчезает, появляется 5 новых. То есть общее количество увеличивается
на 4. Поскольку исходно у нас одна особь, то могло получиться только число, дающее
остаток 1 от деления на 4.
Формула 4x+1, где х - натуральное число, описывает все возможные варианты.
Действительно, чтобы получить 4x+1 особей, достаточно размножить любые х особей.
Задача 1.1.3 (1 балл)
Автобус едет из пункта А в пункт В. При этом в любой момент времени он движется
вправо, чтобы приближаться к пункту В иногда вправо вверх, иногда вправо вниз. Найдите
количество способов доехать. На картинке приведена схема дорог между городами.
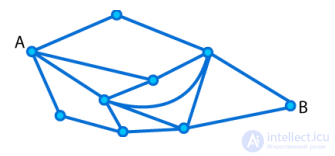
РЕШЕНИЕ:
Расставим количество способов доехать до каждой вершины, двигаясь слева направо.
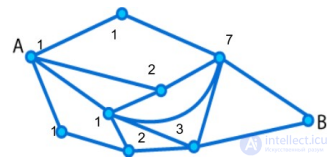
До вершины B 7+3=10 способов. Ответ: 10
Задача 1.1.4 (1 балл)
Автобус едет из пункта А в пункт В. При этом в любой момент времени он движется
вправо, чтобы приближаться к пункту В, иногда вправо вверх, иногда вправо вниз. Найдите
количество способов доехать. На картинке приведена схема дорог между городами.
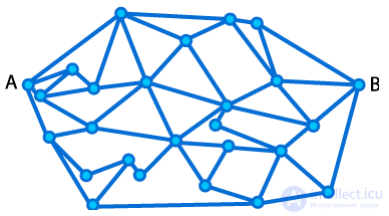
РЕШЕНИЕ:
Расставим количество способов доехать до каждой вершины, двигаясь слева направо.
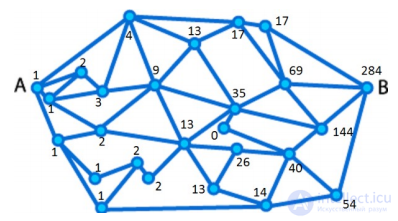
Ответ: 284
Задача 1.1.5 (1 балл)
Незадачливый космонавт Иннокентий почувствовал себя плохо после центрифуги и
не может определить направление, он находится в 5 метрах от комиссии и движется по
прямой. Каждую секунду он с равной вероятностью либо приближается на метр к ней, либо
отдаляется. Если он дошел до комиссии, то больше уже никуда не идет. Найдите вероятность
попадания в руки комиссии не позже чем на 6 секунде.
Решение:
Пусть комиссия находится в пяти метрах справа от космонавта.
Любой путь космонавта за 6 секунд кодируется последовательностью из 6 символов
П или Л (П, если он идет направо и Л - если налево). Всего таких последовательностей 64, из
них нам годятся две: ПППППП и ПППППЛ.
Значит вероятность попасть к комиссии равна 2/64=1/32
Ответ: 1/32
Задача 1.1.6 (1 балл)
Незадачливый космонавт Иннокентий почувствовал себя плохо после центрифуги и
не может определить направление, он находится в 5 метрах от комиссии и движется по
прямой. Каждую секунду он с равной вероятностью либо приближается на метр к ней, либо
отдаляется. Если он дошел до комиссии, то больше уже никуда не идет. Найдите вероятность
попадания в руки комиссии не позже чем на 10-й секунде.
РЕШЕНИЕ:
Изобразим путь космонавта на графике. По вертикальной оси отложим время, а по
горизонтальной расстояние. Изначально космонавт находится в точке s=0, а комиссия в точке
s=5.
На рисунке обозначен путь для последовательности ППЛПППП:
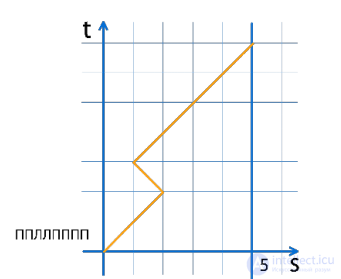
Заметим также, что космонавт может прийти к комиссии только на нечетных шагах.
Таким образом, нас интересует, сколько существует путей, ведущих к комиссии за 5, 7 и 9
секунд.
Переформулируем задачу: сколько существует путей, по сетке на рисунке ниже,
ведущих к прямой s=5. Ходить можно только двигаясь вверх.
Посчитаем количество таких путей для каждой точки, начиная от начальной.
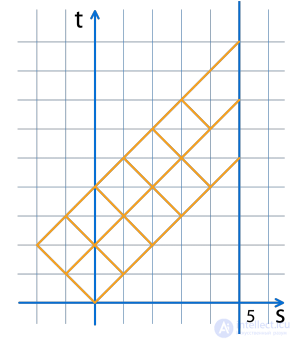
За 5 шагов приводит 1 путь, за 7 - 5 путей, за 9 - 20 путей.
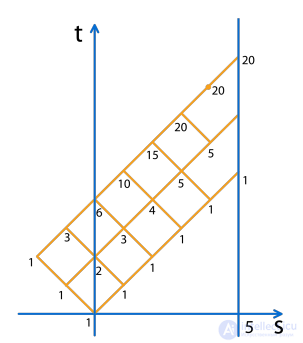
Значит искомая вероятность равна 1/32+5/128+20/512 = 7/64
Ответ: 7/64
Задача 1.1.7 (1 балл)
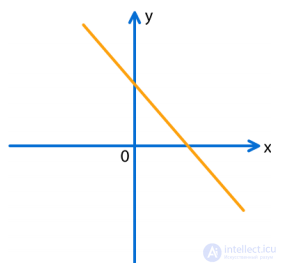
На координатной плоскости задан график функции y=kx+b.
Найдите максимальное значение функции y=kx2+bx.
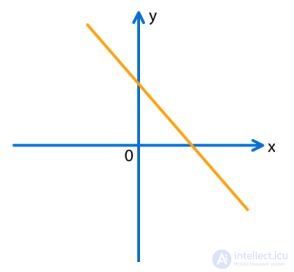
РЕШЕНИЕ:
Поскольку y = kx+b убывает, k<0 y = kx2+bx = x(kx+b) парабола «рожками вниз», с нулями x = 0 и x = -b/k Абсцисса оси параболы x= -b/2k подставим и найдем максимум y=-b2/4k
Задача 1.1.8 (1 балл)
На координатной плоскости задан график функции y=kx+b . Рассмотрите точки пересечения графика этой функции с графиком функции y=kx2+bx. Выберите из этих точек точку с наименьшей абсциссой и выведите в ответе, чему равна эта абсцисса.
РЕШЕНИЕ:
Графиком квадратичной функции y = x(kx + b) является парабола «рогами вниз»,
т.к. k<0
Один из нулей этой функции совпадает с нулем функции y = kx + b, а другой: x = 0.
Между нулями расположена вторая точка пересечения графиков. Одним из корней уравнения
x(kx + b) = kx + b является x = 1, что дает абсциссу второй точки пересечения данного и
искомого графиков.
Ответ: 1
Задача 1.2.1 «Кости» (1 балл)
В некоторых клетках квадратной доски 4×4 находятся четырехгранные игральные
кости. Кость снимается с поля, если количество соседних по стороне непустых клеток
совпадает с числом, выпавшем на кости. Все кости, для которых выполняется это свойство,
снимаются с поля одновременно. Если после снятия костей появляются новые кости, которые
можно снять, то они снимаются по тем же правилам.
Нужно переставить одну кость так, чтобы снялось максимальное количество костей.
Формат входных данных:
На вход программе дается четыре строки по четыре числа в каждом, разделенные
одним пробелом. Все числа — целые неотрицательные, не превышающие 4. Ноль означает
отсутствие кости, любое положительное — наличие кости, на которой выпало указанное
число.
Гарантируется, что на поле есть, по крайней мере, одна кость и одна свободная
клетка

Формат выходных данных:
В виде ответа нужно вывести одно целое число — количество костей, которое можно
снять с доски.
Пример вывода 1:
2
Пример вывода 2:
6
Пояснение. Во втором примере можно переставить единицу с первого ряда в
четвертый, под двойку. Тогда у левой верхней двойки будет два соседа, и она снимется. Так
же с ней снимутся единица в четвертом ряду и единица в четвертом столбце, так как у них по
одному соседу. После этого на доске останутся две единицы и одна двойка — их общий
сосед. Все оставшиеся кости можно снять, так как правило снятия выполняется.
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
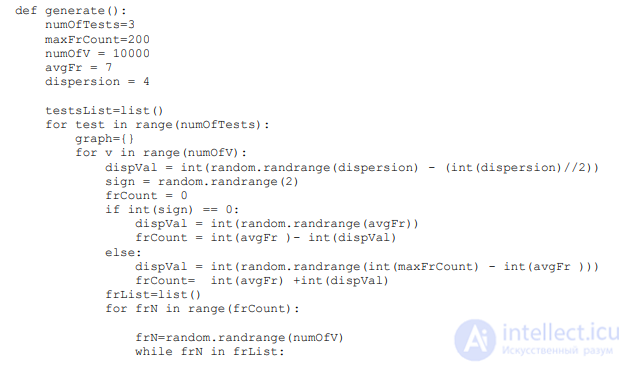
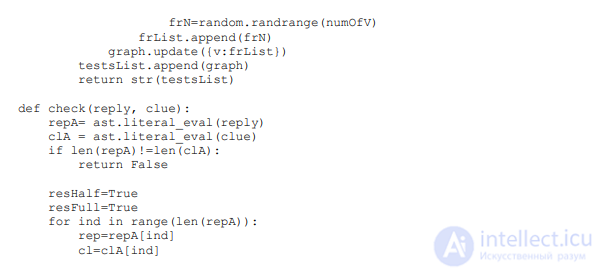
код на языке Python. Функция generate возвращает набор тестов и правильные ответы:


РЕШЕНИЕ:
В этой задаче нужно аккуратно реализовать то, что указано в условии. Пример
программы, реализующей данный алгоритм на языке Python:



Задача 1.2.2 «Корни» (3 балла)
У мальчика Пети есть число N. Но оно ему не нужно, в отличие от числа X. Чтобы
его получить Петя может брать целочисленный корень, умножать и складывать числа.
Целочисленным корнем степени k из натурального числа n будем называть наибольшее
натуральное число, для которого выполняется соотношение: 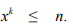 . Например,целочисленным корнем пятой степени из тысячи будет тройка, так как
. Например,целочисленным корнем пятой степени из тысячи будет тройка, так как 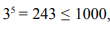 , а 4^5 =1024 > 1000. Обозначим это как
, а 4^5 =1024 > 1000. Обозначим это как 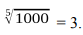 . Также будем считать, что степенью корня могутбыть только натуральные числа.
. Также будем считать, что степенью корня могутбыть только натуральные числа.
Для Пети взятие целочисленного корня— тяжелая задача, и он хочетминимизировать суммарную степень корней, которые встречаются в формуле получения X.
А еще у Пети есть старший брат. Которого зовут Дима. Этот Дима решил добавить
интереса задачке Пети, и дать такие ограничения:
1. Пете нельзя брать корни от чисел, отличных от N.
2. Можно перемножать только те числа, которые Петя получил с помощью операции
взятия корня или умножения других чисел.
3. Складывать можно числа, которые получены как результат умножения, взятия корня
или суммы других чисел.
Помогите Пете написать выражение, которое будет легко считаться и подходит под
ограничения, наложенные Димой. Найдите минимальную сложность искомого выражения.
Формат входных данных:
В единственной строке даны два целых числа N и X (1 ≤ X, N ≤ 1000).
Пример ввода:
100 126
Формат выходных данных:
Выведите единственное натуральное число — ответ на задачу.
Пример вывода:
Пояснение к примеру: 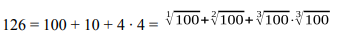
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает набор тестов и правильные ответы:

РЕШЕНИЕ:
Решение состоит из трех этапов. На первом этапе нужно составить набор степеней и
корней из N, которые может быть выгодно использовать. Если два корня с разной степенью
равны, то нам выгодно использовать тот из них, степень которого меньше. Так как 210 >
1000, то для любого N будет не более 11 различных корней. На втором этапе методом
динамического программирования получаем список чисел, которые можно получить
перемножением корней с оптимальной суммарной степенью. На третьем этапе используя тот
же метод получается список чисел, которые можно получить сложением
чисел с предыдущего этапа с оптимальными суммами.
Пример программы, реализующей данный алгоритм на языке Python:



Задача 1.2.3 «Прямая и точки» (3 балла)
На плоскости проведена прямая, проходящая через начало координат. Также на
плоскости выбрано N точек, для каждой известно, с какой стороны от прямой она лежит.
И M точек, для которых нужно ответить на аналогичный вопрос.
Формат входных данных:
В первой строке дано натуральное число N — число точек, для которых известно, с
какой стороны прямой они лежат (1≤N≤100000). В следующих N строках идет описание этих
точек. Каждая строка состоит из трех целых чисел, разделенных пробелом — координаты
точки и указание, с какой стороны лежит точка. Все точки, для которых третье число равно
нулю лежат по одну сторону от прямой, а единице — с другой. Других значений третьего
параметра нет.
В следующей строке дано число M — число точек, для которых нужно указать
сторону (1≤M≤100000). В следующих M строках пары целых чисел — координаты точек.
Координаты всех точек не превышают 1000000 по абсолютному значению.
Гарантируется, что ни одна из точек не лежит на прямой.
Пример ввода:

Формат выходных данных:
Для каждой из M точек выведите 0 или 1 — сторону, с которой лежит точка, в том же
смысле, как и во входных данных. Гарантируется, что ответ единственен.
Пример вывода:
1
0
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает набор тестов и правильные ответы:
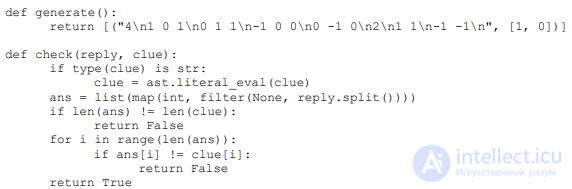
РЕШЕНИЕ:
Если отразить все точки, у которых
«сторона» равна
1, относительно начала
координат, то все точки попадут в некоторый сектор плоскости. Остается найти прямую,
которая не пересекает этот сектор. Ее можно найти следующим образом: находим два луча,
которые образуют границы сектора (например, используя псевдоскалярное произведение).
Искомая прямая будет перпендикулярна биссектрисе этих лучей.
Пример программы, реализующей данный алгоритм на языке Python:


Задача 1.2.4 «Черный ящик» (5 баллов)
Есть черный ящик с двумя вещественными входами и одним бинарным выходом.
Нужно по заданному набору входных и выходных данных максимально точно предсказать
ответы черного ящика на данные из другой выборки входных данных.
Формат входных данных:
В первой строке дано число N — количество входных данных, для которых известны
ответы. В следующих N строках дано по два вещественных и одному натуральному числу,
разделенных пробелами — входные параметры и ответ черного ящика, соответственно.
В следующей строке дано число M — количество входных данных, для которых
нужно узнать ответ. В следующих M строках даны по два вещественных числа, разделенных
пробелом — сами входные данные.
Формат выходных данных:
В ответ нужно вернуть M чисел — предполагаемые ответы черного ящика.
Примечание 1: В этой задаче Вам нужно скачать файл с тестом, решить задачу на
вашем компьютере и вернуть ответ за пять минут. В процессе решения вы можете
пользоваться любыми материалами, языками и программами. Через пять минут после начала
решения задачи тест помечается как устаревший и ответ к нему не принимается. После этого
можно запросить новый тест, при этом таймер запускается заново. Количество попыток не
ограничено. Гарантируется, что все тесты получены с использованием одного черного ящика
с незначительной заменой внутренних констант.
Примечание 2: Эта задача подразумевает возможность частичного решения. В
случае, если правильные ответы даны менее чем для половины входных, то за задачу
начисляется 0 баллов. Если процент правильных ответов превышает 95%, то начисляется 5
баллов. Иначе начисляется 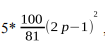 , где p — доля правильных ответов.
, где p — доля правильных ответов.
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает набор тестов и правильные ответы:





РЕШЕНИЕ:
Если нарисовать данный тест на плоскости, считая пары чисел как координаты, то
можно заметить, что есть одна зона, в которую попадают все точки с одним ответом и две,
куда попадают остальные. Причем границы этих областей имеют простую структуру. Дальше
можно было либо понять, что граница представляет собой гиперболу и восстановить ее
параметры, либо воспользоваться специальными инструментами, либо реализовать
подходящий алгоритм машинного обучения, например, «метод трех соседей»: выбираем для
изучаемой точки три ближайших. Ответ для точки будет совпадать с преобладающим ответом
среди соседей.
Пример программы, реализующей данный алгоритм на языке Python:
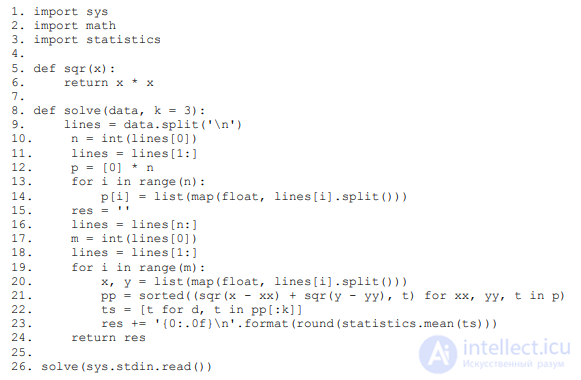

Количество баллов, набранных при решении всех задач суммируется. Призерам
первого отборочного этапа необходимо набрать 7 баллов (для 9 класса) и 9 баллов (для 10-11
класса). Победители первого отборочного этапа должны набрать 20 баллов.
Второй отборочный этап проводится в командном формате в сети интернет, работы
оцениваются автоматически средствами системы онлайн-тестирования. Продолжительность
второго отборочного этапа составляет 2 недели. Задачи носят междисциплинарный характер
и в более простой форме воссоздают инженерную задачу заключительного этапа. Решение
задач предполагало написание программ, допускалось использовать язык программирования
Python. Решение каждой задачи дает определенное количество баллов. В данном этапе можно
получить суммарно от 0 до 45 баллов.
Задача 2.1.1 (10 баллов)
В летний лагерь приехало 1000 школьников. Когда школьник приезжал, его сразу
переписывали (ставили порядковый номер начиная с нуля — каким школьник приехал в
лагерь). Школьников сразу разбивали по отрядам с разным количеством человек в отряде:
первые n1 школьников определили в первый отряд, следующие n2 школьников — во второй
отряд, следующие n3 — в третий и так далее.
Однажды все четные отряды увезли на экскурсию. И в лагерь приехала комиссия и
переписала всех школьников, которые остались (каждый школьник назвал номер, каким его
записали, когда он приехал в лагерь). По ошибке некоторых школьников переписали
несколько раз. Как теперь разобраться, какой школьник в каком отряде?
На вход подается массив из чисел, соответствующих порядковым номерам
переписанных школьников, которые остались в лагере.
На выход подаются набор пар чисел: порядковый номер первого и конечного
школьника в первом отряде, порядковый номер первого и конечного школьника во втором
отряде и так далее.
За успешное решение задачи участники получают 10 баллов.
Пример ввода:




Пример вывода:
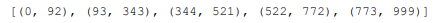
Ограничение по времени исполнения программы: 15 с
Ограничение по использованию оперативной памяти: 256 Мб
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает возвращает набор тестов и правильных
ответов:

РЕШЕНИЕ:
Необходимо понять, что раз номера идут подряд,то после сортировки всех предложенных номеров, заполненные подряд идущие интервалы номеров будут нечетные отряды, а отсутствующие интервалы - четные. После этого существует несколько подходов к
решению, но все они так или иначе связаны с сортировкой массива. Один из подходов
подразумевает использование сортировки слиянием, добавляя новые элементы в уже
отсортированный массив номеров школьников, заполняя при этом интервалы. Второй
состоит в заполнении массива и дальнейшей сортировкой стандартными встроенными
алгоритмами и втором проходе по массиву выделяя заполненные интервалы.
Код программы на языке Python:



Задача 2.1.2 (15 баллов)
Картограф составлял для каждого города список городов, с которыми он связан
дорогами. Теперь его спрашивают о том, можно ли проехать между двумя далекими
городами.
На вход подается два названия города, которые нужно проверить и дальше идет идет
перечисление для городов, с какими другими городами он связан дорогой. Ответ необходимо
давать в формате True и False.
За успешное решение задачи участники получают 15 баллов.
Пример ввода:

Ограничение по времени исполнения программы: 3000 с
Ограничение по использованию оперативной памяти: 256 Мб
СПОСОБ ОЦЕНКИ РАБОТЫ:
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает набор тестов и правильные ответы.
Пример нескольких тестов с правильными ответами представлен ниже:


РЕШЕНИЕ:
Необходимо распознать в задаче проблему поиска пути между двумя вершинами в
графе. Школьникам необходимо выбрать способ представления графа в памяти и
осуществить поиск в ширину (Bread-first search) от одной вершины к другой. Если алгоритм
закончил работу не встретив второй вершины, то пути нет, иначе — есть.
Код решения на языке Python:









Задача 2.1.3 (0-20 баллов)
В задаче фигурирует придуманный нами граф социальной сети
(для каждого
пользователя указано, какие пользователя добавили его в друзья). Об этом говорит сайт https://intellect.icu . Для каждого пользователя
вычисляется его популярность, она основана на том, сколько людей дружит с теми
пользователями, с которым он дружит.
Популярность вычисляется как X - суммарное количество людей, которые дружат с его друзьями, считая его самого.
Необходимо рассчитать два перцентиль 50 и 90, т.е. два наименьших значенияпопулярности такие, что с вероятностью 50% для первого и 90% для второго популярность
случайного пользователя будет меньше данного значения.
Задачу необходимо решить у себя на компьютере и в систему загрузить решение в
виде двух чисел для каждой задачи.
Если для всех тестов вы посчитали хотя бы перцентиль 50 (с вероятностью 50
процентов популярность окажется меньше), то вы получаете половину баллов от задачи.
Пример ввода:

Пример вывода:
[(4, 6), (7, 9)]
Ограничение по использованию оперативной памяти: 256 Мб
Время одной попытки: 5 мин
СПОСОБ И КРИТЕРИЙ ОЦЕНКИ РАБОТЫ:
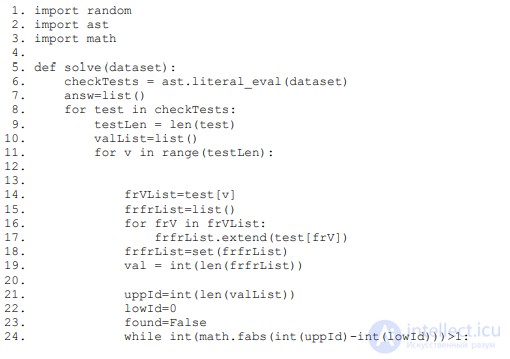
Для генерации уникального условия и проверки результата используется следующий
код на языке Python. Функция generate возвращает набор тестов и правильные ответы:
Функция проверки check возвращает показатель точности решения (от 0 до 1). Это
значение умножается на 20, что дает число баллов, полученных командой.
РЕШЕНИЕ:
Для данное задачи необходимо сначала принять решение о внутреннем
представлении данных графа социальной сети. После этого для всех пользователей
рассчитать значение популярности. Затем необходимо отсортировать пользователей по
популярности (основываясь на знаниях из первой задачи) и взять соотвествующий элемент
массива (средний для перцентиля 50 и находящийся на позиции 0.9*N где N-число элементов
массива, для перцентиля 90).
Код программы на языке Python:

продолжение следует...
Часть 1 Машинное обучение на больших данных Теория и примеры решения задач
Часть 2 2.2. Критерии определения призеров и победителей - Машинное обучение на
Часть 3 4.3. Методика расчета баллов - Машинное обучение на больших данных
Комментарии
Оставить комментарий
Машинное обучение
Термины: Машинное обучение