2.2. Критерии определения призеров и победителей - Машинное обучение на

Это продолжение увлекательной статьи про машинное обучение на больших данных .

...

data-auto-open loading="lazy" alt="Машинное обучение на больших данных Теория и примеры решения задач" >

2.2. Критерии определения призеров и победителей

Количество баллов, набранных при решении всех задач, суммируется. Призерам

второго отборочного этапа было необходимо набрать 10 баллов (для учащихся 9 класса) и 15

баллов (для учащихся 10-11 класса). Победители второго отборочного этапа должны были

набрать 45 баллов.

§3 Заключительный этап: индивидуальная часть

Заключительный этап олимпиады состоит из двух частей: индивидуальное решение

задач по предметам (математика, информатика) и командное решение инженерное задачи. На

индивидуальное решение задач дается по 2 часа на один предмет. Задачи по математике и

информатике общие на параллели 9 и 10-11 класс. Решение каждой задачи дает определенное

количество баллов (см. критерии оценки далее). По математике за каждую задачу можно

получить от 0 до указанного количества баллов в соответствии с описанными критериями.

Баллы по информатике зачисляются в полном объеме за правильное решение задачи.

Решение задач по информатике подразумевало написание задач на языке Python. Участники

получают оценку за решение задач в совокупности по всем предметам данного профиля

(математика и информатика) — суммарно от 0 до 24 баллов.

3.1. Задачи по математике

Задача 3.1.1 (макс. 6 баллов)

Группа психологов разработала тест, пройдя который, каждый человек получает

оценку - число Q - показатель его умственных способностей (чем больше Q, тем больше

способности). За рейтинг страны принимается среднее арифметическое значений Q всех

жителей этой страны.

Задание 3.1.1а (1 балл). Группа граждан страны А эмигрировала в страну Б.

Покажите, что при этом у обеих стран мог вырасти рейтинг.

Задание 3.1.1б (3 балла). После этого группа граждан страны Б (в числе которых

могут быть и бывшие эмигранты из А) эмигрировала в страну А. Возможно ли, что рейтинги

обеих стран опять выросли?

Задание 3.1.1в (2 балла). Группа граждан страны А эмигрировала в страну Б, а

группа граждан Б - в страну В. В результате этого рейтинги каждой страны оказались выше

первоначальных. После этого направление миграционных потоков изменилось на

противоположное — часть жителей В переехала в Б, а часть жителей Б - в А. Оказалось, что

в результате рейтинги всех трех стран опять выросли (по сравнению с теми, которые были

после первого переезда, но до начала второго).

(Так, во всяком случае, утверждают информационные агентства этих стран.) Может ли такое быть (если да, то как, если нет, то

почему)?

(Предполагается, что за рассматриваемое время Q граждан не изменилось, никто не умер и не родился.)

РЕШЕНИЕ:

а) Пусть, например, в А жили всего два человека с показателями 3 и 5, а в Б - один

человек с показателем 1. После переезда человека с показателем 3 из А в Б в обеих странах

рейтинг повысится.

б) Сначала заметим, что если все население страны разбито на две группы X и Y с рейтингами соответственно ,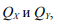

то рейтинг Q всей страны находится между 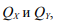(причем равенство будет только в случае QX = QY).

Обозначим через a и b рейтинги стран А и Б до эмиграции из А в Б, через a1 и b1 -

рейтинги этих стран после этой эмиграции, а через c - рейтинг группы эмигрантов. По

условию a < a1. Отсюда, как показано выше, следует, что c < a < a1

(до эмиграции А разбита на группу эмигрантов с рейтингом c и группу остающихся с рейтингом a1).

Аналогично b < b1 < с. Итак, b < a и b1 < a1. Первое неравенство показывает, что

увеличение рейтингов обеих стран возможно только при эмиграции из страны с большим

рейтингом в страну с меньшим рейтингом. Второе неравенство показывает, что рейтинг

страны А остался выше рейтинга страны Б. Таким образом, одновременное увеличение

рейтингов при эмиграции из Б в А невозможно.

в) Пусть в стране А всего два жителя с показателями Q = 1 и 2, в стране Б - четыре

жителя (Q = 2, 2, 4, 10), в стране В - один житель (Q = 1). При первой волне эмиграции из

А в Б эмигрировал один человек с Q = 1, а из Б в В - двое с Q = 2. При второй волне из В в

Б переехал один человек с Q = 1, а из Б в А - двое с Q = 1 и 4. Рейтинги стран при этом

менялись так: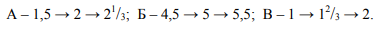

Критерии оценки:

• (а) приведен любой верный пример - 1 балл

• (б) доказательство основывается на неверном утверждении, но может быть доведено до правильного - 1 балл

◦ в доказательстве используются верные утверждения, которые не доказаны - 2 балла

◦ полное доказательство - 3 балла

•(в) приведен пример, как такое возможно - 2 балла

Задача 3.1.2 (6 баллов)

Администрация социальной сети ВКонтакте решила создать сообщество «Всех тех, у кого меньше половины друзей состоит в этом сообществе». Для этого им нужно включить в сообщество пользователей так, чтобы в итоге:

 у всех, кто в этом сообществе, меньше половины друзей были в нем же;

 у всех, кто не в этом сообществе, не меньше половины друзей были в нем.

Всегда ли им удастся создать такое сообщество?

(Предполагается, что пользователи не сами вступают в сообщество, а распределяются администрацией социальной сети)

РЕШЕНИЕ:

Представим социальную сеть в виде графа. Вершины - пользователи, ребра -

отношения дружбы. Тогда нам надо доказать, что любой граф можно покрасить в два цвета:

синий и красный, так чтобы

 у синих вершин меньше половины соседей были синими

 у красных вершин не меньше половин соседей были синими

Покрасим граф как-нибудь. Теперь будем перекрашивать вершины, для которых не выполнено условие.

Если перекрашиваем красную вершину (у нее меньше половины синих соседей), количество ребер между синими и красными увеличивается.

Если перекрашиваем синюю (у менее не меньше половины синих соседей),

количество ребер между синими и красными не уменьшается, а количество красных увеличивается. Поэтому перекраска не может идти бесконечно. Значит в какой-то момент для всех вершин будут выполнены необходимые условия.

Ответ: да, всегда

Критерии оценки:

• доказано, что в любой сети такое возможно — 6 баллов

• есть верные идеи инварианта, но в доказательстве есть пробелы — 3 балла

3.2. Задачи по информатике

Задача 3.2.1 «Всюду реклама» (1 балл)

Когда-то давно Паша создал свой интернет-портал. Теперь его сайт стал достаточно популярным, и молодой человек решил, что пришло время его монетизировать. Если конкретнее, он решил вводить рекламу. Стандартным решениям Паша не доверяет, поэтому решил написать свою небольшую рекламную платформу.

На сайте есть N рекламных блоков. Про каждый блок известна его выгодность v_i, а именно, сколько раз на него кликнули за последний месяц(количество кликов не зависит от содержания объявления). Через форму заявок Паше поступило M рекламных объявлений от рекламодателей. Каждый рекламодатель указывает для своего объявления цену c_i в рублях, которую он готов заплатить за 100 кликов.

Паша считает, что чем больше рекламодатель готов заплатить, тем более выгодное

место его объявление должно занимать. Если объявлений слишком много, то объявления с

очень маленькой ценой показаны не будут, если объявлений слишком мало, то самые

невыгодные блоки останутся пустыми.

От вас требуется сопоставить рекламные объявления и рекламные блоки на сайте в

соответствии с Пашиными принципами.

Формат входных данных:

В первой строке даны два числа

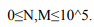N — количество рекламных блоков

на сайте и M — количество рекламных объявлений. Во второй строке через пробел даны N

чисел vivi. Число 0≤v_i≤5000 характеризует выгодность i-ого рекламного объявления. В

третьей строке через пробел даны M чисел 0≤c_j≤10000. Число c_j показывает цену, которую

готов заплатить рекламодатель за 100 кликов на j-ое объявление.

Формат выходных данных:

Выведите N строк, в каждой строке выведите пару чисел: выгодность рекламного

блока и цену за 100 кликов соответствующего ему рекламного объявления, которое будет

располагаться в этом блоке. Если на данное место не хватило рекламного объявления, вместо

номера объявления укажите -1.

Если решений больше одного, выведите любое.

СПОСОБ ОЦЕНКИ РАБОТЫ:

Для генерации уникального условия и проверки результата используется следующий

код на языке Python. Функция generate возвращает набор тестов и правильные ответы:

РЕШЕНИЕ:

В данной задаче работает идея жадных алгоритмов. По условиям мы сопоставляем

максимальный элемент из набора объявлений с максимальным элементом из набора

рекламных блоков. Второе по цене объявление располагаем на второе по стоимости место. И

так далее. Следовательно, достаточно отсортировать оба массива по возрастанию и взять

первые N пар элементов. Необходимо учитывать, что если M < N, То в последних M-N

записях необходимо вместо стоимости c выводить -1.

Реализация этого алгоритма на языке программирования Python:

Задача 3.2.2 «Кто на свете всех умнее?» (1 балл)

Исследование данных требует внимания к деталям и усидчивости, пусть и не очень

большой. Сегодня к вам в руки попал файл с данными, которые управление районом

собирает обо всех учениках. Многие из этих данных могут приоткрыть специалистам

информацию о том, какие факторы и как влияют на хорошее обучение учеников.

На данный момент управление районом интересует два вопроса:

во-первых, ему важно знать средний возраст школьников, которые ходят на

дополнительные занятия в школах. А во-вторых, фамилию и имя школьника, с

максимальным баллом по химии, среди тех, кто учится в 8 или 9 классе.

Формат входных данных:

В первой строке задано число школьников 1≤N≤10^5, чьи данные собрала школа.

Следующие N строк содержат данные об учениках. Каждая строка имеет вид ['Имя',

'Фамилия', 'Отчество', число полных лет, ['школа (номер или название)', класс, тип каникул

('t'/'q')],

[средний балл по математике(число от 1 до 10), средний балл по русскому языку

(число от 1 до 10), средний балл по физике (число от 1 до 10), средний балл по химии (число

от 1 до 10), средний балл по биологии (число от 1 до 10)], количество дополнительных

занятий в школе, количество детей в семье ребенка].

Формат выходных данных:

В первой строке выведите средний возраст школьников, которые ходят на

дополнительные занятия в школе, округленное вниз до ближайшего целого числа. Во второй

строке через пробел выведите фамилию и имя школьника, с максимальным баллом по химии,

среди тех, кто учится в 8 или 9 классе. Если детей с одинаковым баллом несколько, выведите

того, кто в файле записан раньше. Если ответ на какой-то вопрос не может быть корректно

получен, замените отсутствующий ответ на строку "No answer".

СПОСОБ ОЦЕНКИ РАБОТЫ:

Для генерации уникального условия и проверки результата используется следующий

код на языке Python. Функция generate возвращает набор тестов и правильные ответы:

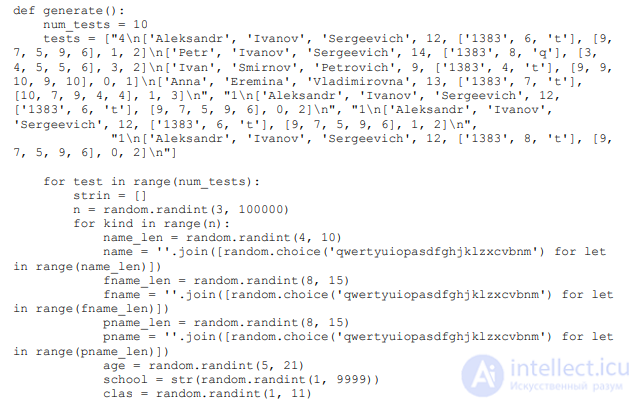
РЕШЕНИЕ:

Так как задача поиска максимального, минимального и среднего значения на

неотсортированном потоке данных может быть решена за время сравнимое со временем

считывания, хорошее решение построчно считывает данные о школьниках. Перед

считывание k-ой строки хорошее решение знает ответ для файла состоящего из первых k-1

строк исходного файла. На k-ом шаге необходимо выделить данные из строки и обновить

следующие переменные в соответствии с условиями:

 количество школьников, которые ходят на дополнительные занятия;

 суммарный возраст школьников, которые ходят на дополнительные занятия;

 фамилия и имя восьми-/девятиклассника с максимальным баллом по химии;

 максимальный балл по химии среди восьми-/девятиклассников.

Когда обработаны все записи, необходимо проверить, что существует хотя бы один

8/9классник и, что существует хотя бы один школьник, который ходит на допзанятия. Если

таких школьников не существует, то необходимо вывести “No answer” на соответствующий

вопрос.

Реализация этого алгоритма на языке программирования Python:

Задача 3.2.3 «Субботник» (3 балла)

На следующих выходных ученики всех классов отправятся на субботник в парк.

Ребята хотят сами разделиться на команды. Было решено, что для того чтобы попасть в

определенную группу, у школьника обязательно должен быть в этой группе хотя бы один

друг. Считается, что если первый школьник дружит со вторым, то и второй дружит с первым.

Каждая команда поедет на субботник на отдельном автобусе, поэтому количество команд

должно быть минимальным.

Осталось только заказать автобусы и составить списки для каждого автобуса, кто из

учеников в нем едет. Составьте программу, которая решит эту задачу.

Формат входных данных:

В первой строке задано два числа: N — число школьников, M — число строк,

описывающих отношения дружбы между школьниками 0≤N,M≤1000. В следующих M

строках даны пары натуральных чисел 1≤a,b≤N, означающие что школьник номер a дружит

со школьником под номером b.

Формат выходных данных:

В первой строке выведите T — число автобусов. В следующих T строках выведите

информацию о школьниках, которые едут в автобусах, в порядке возрастания номеров

школьников. Во второй строке укажите в квадратных скобках число школьников, далее через

пробел в порядке возрастания номера школьников, которые едут в первом автобусе, если

необходимо, в третьей строке — в квадратных скобках число школьников, далее номера

школьников, которые едут во втором автобусе, и так далее. Каждый школьник должен

присутствовать в одном и только одном автобусе. Если возможно несколько ответов,

выведите любой.

СПОСОБ ОЦЕНКИ РАБОТЫ:

Для генерации уникального условия и проверки результата используется следующий

код на языке Python. Функция generate возвращает набор тестов и правильные ответы:

РЕШЕНИЕ:

У автобусов нет максимального ограничения по количеству учеников, которые в нем

едут. Из этой посылки и условия, что в решении должно быть минимальное число автобусов,

легко вывести идею, что оптимальное решение не будет разделять ни одну пару школьников,

которые между собой дружат.

Таким образом суть задачи в выделении компонент связности для

неориентированного графа. Эту задачу можно решать, например, используя поиск в ширину

или поиск в глубину.

Пример программы, реализующей этот алгоритм, на языке Python:

Задача 3.2.4 «Итоговая аттестация» (3 балла)

Конец года — беспокойное время не только для школьников, которые готовятся к

экзаменам, но и для составителей экзаменационных заданий. Составляя любой тест,

необходимо учитывать, насколько сложной будет задача для школьников, и определить,

сколько учащихся сдадут тест успешно.

В этом году было решено провести тестовый экзамен, пригласив 100 учеников

разных школ решить 5 задач. Каждая задача оценивается в ai баллов. Задача либо решена на

полный балл, либо не решена совсем, а значит за нее не начисляются баллы. Частичные

решения проверяющие не учитывают. После экзамена составители получили результаты

школьников. Для каждого школьника известны результаты проверки всех задач.

Необходимо посчитать, сколько школьников получит не менее K баллов, если

экзамен будут сдавать 1000000 школьников.

Обратите внимание, что невозможно достаточно надежно найти вероятность решить

определенный набор задач, но будем считать, что возможно достаточно надежно оценить

вероятность решить одну задачу.

Формат входных данных:

В первой строке дано число K — число баллов, необходимое для успешной сдачи

теста. Во второй строке 5 натуральных чисел — баллы за задачи. Первое число соответствует

баллам за первую задачу, второе — за вторую и так далее.

Далее следует 100 строк. В каждой строке 5 чисел, обозначающих, решена ли

соответствующая по номеру задача или нет. На первом месте в строке указано решена ли

первая задача, на втором решена ли вторая, и так далее. Если задача решена, то в строке будет

указана 1, если нет — 0.

Формат выходных данных:

В единственной строке выведите ожидаемое число людей, которые успешно сдадут

тот же тест если решать его будет 1000000 школьников.

СПОСОБ ОЦЕНКИ РАБОТЫ:

Для генерации уникального условия и проверки результата используется следующий

код на языке Python. Функция generate возвращает набор тестов и правильные ответы:

def generate():

num_tests = 10

tests = []

for test in range(num_tests):

num_tasks = 5

points = []

for i in range(num_tasks):

points.append(random.randint(1, 100))

sum_points = sum(points)

results = []

for i in range(100):

results.append(' '.join([random.choice(['0', '1']) for i in

range(num_tasks)]))

good_points = random.randint(0, sum_points)

test_case = "{}\n{}\n{}\n".format(good_points, ' '.join([str(point) for

point in points]), '\n'.join(results))

tests.append(test_case)

return tests

def check(reply, clue):

return int(reply) - int(clue) < int(2)

РЕШЕНИЕ:

Считаем, сколько участников решили каждую задачу. Из этого определяем

вероятность решить определенную задачу.

Исходя из этой информации вычисляем вероятность решить определенный набор

задач. Если этот набор задач соответствует успешному прохождению тестирования,

увеличиваем суммарную вероятность успешно пройти тест.

Пример правильной программы на языке Python:

01. good_point = int(input())

02. points = list(map(int, input().split()))

03. tasks_res = * 5

04. p = * 5

05. for i in range(100):

06.

sh_res = list(map(int, input().split()))

07.

for j in range(5):

08.

tasks_res[j] += sh_res[j]

09. for i in range(5):

10.

p[i] = tasks_res[i] / 100

11. sum_p = 0

12. for a0 in (0, 1):

13.

for a1 in (0, 1):

14.

for a2 in (0, 1):

15.

for a3 in (0, 1):

16.

for a4 in (0, 1):

17.

if a0 * points + a1 * points + a2 * points + a3

* points + a4 * points >= good_point:

18.

tmp = 1

19.

tmp =(tmp*(1-p )) if a0==0 else (tmp*p )

20.

tmp =(tmp*(1-p )) if a1==0 else (tmp*p )

21.

tmp =(tmp*(1-p )) if a2==0 else (tmp*p )

22.

tmp =(tmp*(1-p )) if a3==0 else (tmp*p )

23.

tmp =(tmp*(1-p )) if a4==0 else (tmp*p )

24.

sum_p += tmp

25. print(int(1000000*sum_p))

Задача 3.2.5 «Минимальное остовное дерево» (4 балла)

Когда мы работаем с неориентированными графами, часто возникает следующая

задача: сделать граф как можно меньше, но так, чтобы все вершины остались соединены друг

с другом. Например, представьте, что вы хотите построить железную дорогу между

несколькими городами и вам принесли огромную карту, на которой проложены все

возможные варианты железнодорожных путей и цены их постройки. Вы хотите из всех путей

взять минимально необходимый набор, чтобы все города были связаны друг с другом, но

сама постройка железнодорожной сети обошлась как можно дешевле.

Города и дороги образуют взвешенный неориентированный граф. Города - вершины

графа, дороги - ребра, цены дорог - веса ребер. Теперь наша задача свелась к чистой

математике: нам нужно выбрать в графе некоторый набор ребер, такой, что граф остается

связным, а суммарный вес ребер наименьший возможный.

Нетрудно заметить, что для того, чтобы соединить N городов, нам необходима N−1

дорога. Также понятно, что если какие-то из выбранных дорог образуют цикл, значит можно

было какую-то из дорог в этом цикле не строить, но транспортная сеть осталась бы связной.

А раз ее можно было не строить, значит результат можно было бы получить дешевле.

Связные графы, в которых число ребер на единицу меньше числа вершин и не имеют циклов,

называются деревьями. Значит нам нужно получить как раз дерево, но не любое, а самое

дешевое. Самое дешевое дерево, соединяющее все вершины графа, называется

минимальным остовным деревом.

Для того, чтобы построить минимальное остовное дерево, можно воспользоваться

алгоритмом Крускала. Его идея очень простая: мы будем добавлять дороги по одной, начиная

с самой дешевой. Но если дорога соединяет какие-то города, между которыми уже есть

проезд, то эта дорога бесполезна (она создаст цикл) и брать ее мы не будем, а возьмем

следующую по цене дорогу. Через N−1 шаг мы объединим все N городов, если это было

возможно. Теперь разберем алгоритм чуть детальнее. Вашей задачей будет реализовать его в

виде программы на Python.

На каждой итерации нашего алгоритма города и построенные дороги образуют

несколько несвязных. Изначально эти деревья очень маленькие, каждое дерево состоит из

одной единственной вершины-города, а ребер-дорог никаких нет. Пронумеруем города.

Также мы будем нумеровать деревья и про каждую вершину будем хранить информацию о

том, к какому дереву она относится (нам это нужно, чтобы точно понимать, какие вершины

соединять нет необходимости). Изначально каждая вершина принадлежит номеру с таким же

номером, как у самой вершины, эту информацию мы сохраним в специальный массив, в

котором будут храниться номера деревьев каждой вершины. На каждой итерации мы будем

объединять ребром два дерева в одно; при этом нам придется менять этот массив, чтобы

показать, что вершины из объединенных деревьев теперь принадлежат одному дереву.

Например, мы можем взять все вершины из второго дерева (мы ведь знаем номер этого

дерева) и указать, что теперь эти вершины принадлежат первому дереву

(для этого

достаточно в массиве в соответствующие элементы записать номер первого дерева).

Теперь нам осталось только выбрать, какие ребра выбирать. Для начала создадим

массив, в котором будут все возможные ребра, и отсортируем его по весу от наименьшего к

наибольшему. Теперь мы будем перебирать все ребра по-порядку и выбирать, какие из них

добавить, а какие пропустить. Если ребро соединяет две вершины разных деревьев, мы его

берем в наш минимальный остов, попутно объединяя эти два дерева. Если ребро соединяет

две вершины, которые уже принадлежат одному дереву, мы его пропускаем и переходим к

следующему.

Формат входных данных:

Первая строка входного файла содержит два натуральных числа N и M - количество

вершин и ребер графа соответственно 1≤N≤1000,0≤M≤2000. Следующие M строк содержат

описание ребер по одному на строке. Ребро номер i описывается тремя натуральными

числами bi, ei, wi — номера концов ребра и его вес соответственно 1≤bi,ei≤N,0≤wi≤100000.

Гарантируется, что граф состоит из одной компоненты связности.

Формат выходных данных:

Выведите единственное целое число — вес минимального остовного дерева.

СПОСОБ ОЦЕНКИ РАБОТЫ:

Для генерации уникального условия и проверки результата используется следующий

код на языке Python. Функция generate возвращает набор тестов и правильные ответы.

Пример нескольких тестов представлен ниже:

def generate():

num_tests = 10

tests = [("4 4\n1 2 1\n2 3 2\n3 4 5\n4 1 4\n", "7\n"),

("5 10\n4 3 3046\n4 5 90110\n5 1 57786\n3 2 28280\n4 3 18010\n4 5 61367\n4 1

18811\n4 2 69898\n3 5 72518\n3 1 85838\n", "107923\n"),

("2 1\n1 2 10986\n", "10986\n"),

("3 2\n1 3 15891\n3 2 90498\n", "106389\n"),

("10 17\n8 7 83353\n7 10 74636\n7 4 47938\n10 3 4456\n8 1 90055\n3 6 22856\n10 5

84755\n3 9 77963\n5 2 58908\n8 4 44704\n8 3 36890\n8 5 28033\n8 2 30743\n7 10

83866\n7 4 95412\n7 3 48170\n7 6 38877\n","374577\n"),

#...

("6 9\n1 5 1\n5 6 3\n6 2 4\n6 3 5\n5 4 2\n1 4 3\n2 3 6\n1 2 5\n3 4 7\n",

"15\n")]

return tests

def check(reply, clue):

return int(reply) == int(clue)

РЕШЕНИЕ:

Алгоритм решения подробно описан в условии задачи. Задача требует внимательной

реализации.

01. n, m = map(int, input().split())

02. gr = []

03. tree_num = [i for i in range(n)]

04. for i in range(m):

05.

b, e, w = map(int, input().split())

06.

gr.append((w, b-1, e-1))

07.

08. gr.sort()

09. ans = 0

10. for reb in gr:

11.

if tree_num[reb ] == tree_num[reb ]:

12.

continue

13.

ans += reb

14.

min_num = min(tree_num[reb ], tree_num[reb ])

15.

max_num = max(tree_num[reb ], tree_num[reb ])

16.

for i in range(n):

17.

if tree_num[i] == max_num:

18.

tree_num[i] = min_num

19. print(str(ans))

tree_num — массив, в котором на i-ом месте номер дерева к которому сейчас

относится i-ая вершина

§4 Заключительный этап: командная часть

Постановка задачи. Участникам командной части заключительного этапа было

необходимо решить серию задач по анализу графа пользователей социальных сетей:

предсказать возраст пользователей, не указавшего его в своем профиле; предсказать регион

проживания пользователя; предположить, кто из других пользователей социальной сети

является знакомым пользователя.

Участники должны были писать программы на языке Python. Продолжительность

командной части заключительного этапа

— 3 дня (всего 18 астрономических часов).

Участники имели доступ к сети Интернет и могли пользоваться своими телефонами и

ноутбуками.

Всего командам предлагалось 3 задачи — по одной на каждый день. Условие задачи

становилось известно участникам утром соответствующего дня. Каждая задача оценивалась

в баллах (подробнее см. далее).

Для каждой задачи было подготовлено два подграфа реальной социальной сети

«Одноклассники»:

1. участникам

представлялся

специально подготовленный, очищенный и

анонимизированный подграф;

2. проверка качества решения осуществлялась автоматически на полном графе, в

котором присутствовали данные, вычищенные из первого графа.

Для каждой задачи участникам предоставлялось работающее базовое решение с

низкой эффективностью, и участники стояли перед выбором: программировать с нуля свое

собственное решение, которое сможет решить поставленную задачу качественнее, или

дорабатывать предложенное решение. При этом можно было использовать базовое решение

частично, например только модель данных или только распознаватель входных данных.

4.1. Описание исходных данных

Во всех задачах участникам предоставлялся граф пользователей

(связи между

пользователями) и файл с демографией

(анонимизированные данные по каждому

пользователю).

4.1.1. Граф пользователей

Граф сохранен в формате разреженной матрицы, где по каждой связи есть

информация о ее типе (родственник, друг и т.д.) в виде битовой маски. Каждая строка

матрицы соответствует друзьям одного пользователя и имеет формат:

ID_пользователя1 {(ID_друга1,маска1), (ID_друга2,маска2),…}

Матрица партиционирована по ID пользователя на 16 файлов, каждый из которых

сжат стандартным протоколом сжатия GZip.

Пары в списке связей отсортированы по ID друга (по возрастанию). Пример записей

из графа:

102416

{(5362439,0),(7321627,0),(7345280,0),(9939258,0),(9976393,0),(11260492,0),

(11924364,0),(16498676,0),(16513827,0),(21716731,0),(21826340,0),(23746537,0),

(23751503,0),(24412936,0),(24423533,0),(30287856,0),(32321147,0),(34243036,0),

(37592142,0),(39485706,0),(41505243,0),(42791620,0),(52012206,0),(52671472,0),

(54652307,0),(57293803,0),(59242794,0),(59252048,0),(62535397,0),(62563866,0),

(62567154,0),(64588902,0)}

102608

{(4167808,32784),(6019974,32),(6152844,16),(9570536,64),(10699806,33),

(13290514,0),(15064491,128),(16432948,512),(24473204,0),(24655822,0),

(25833075,256),(28000951,64),(30834507,2048),(34567533,16),(35766667,0),

(37385121,0),(40123805,512),(43134386,1024),(45439608,0),(45484652,0),

(47562525,0),(52378153,256),(52403136,512),(52493894,1024),(53483990,0),

(54048767,0),(54286279,2048),(57401158,0),(57956631,0),(58183281,0),

(61117236,32),(61898065,0),(61936634,0),(64512205,512),(65014849,0),

(65112662,0),(65259449,0)}

В маске связи могут быть установлены следующие биты:

1.

Любовь

2.

Супруг или Супруга

3.

Родитель

4.

Ребенок

5.

Брат или сестра

6.

Дядя или тетя

7.

Родственники

8.

Близкие друзья

9.

Коллеги

10. Одноклассники

11. Племянник

12. Дед или бабушка

13. Внук или внучка

14. Однокурсник

15. Дружба в армии

16. Приемный родитель

48

17. Приемный ребенок

18. Крестный отец

19. Крестный сын

20. Совместная игра в спортивные игры

Помимо перечисленных битов в маске отношений может быть установлен, а может и

не быть установлен нулевой бит. Этот бит играет чисто техническую роль и не имеет

физического смысла. В итоге, например, отношение типа Ребенок может кодироваться

числами 16 или 17.

Данные были подготовлены с использованием инструмента для хранения больших

данных Apache Pig и содержат два соответствующих файла с заголовками, позволяющие

участникам использовать этот инструмент и для предварительной обработки/фильтрации

данных.

4.1.2. Демография пользователей

Данные о демографии предоставлены для того же миллиона пользователей, что и

информация о социальных связях в формате списка атрибутов:

userId create_date birth_date gender ID_country ID_Location loginRegion

где:

• userId - идентификатор пользователя

• create_date - дата создания пользовательского аккаунта (количество миллисекунд

от 01.01.1970)

• birth_date - дата рождения пользователя (количество дней от 01.01.1970, может

быть отрицательным!)

• gender - пол пользователя (1 - мужчины, 2 - женщины)

• ID_country - идентификатор страны, указанной в профиле

• ID_Location - идентификатор региона/города, указанный в профиле.

• loginRegion - идентификатор региона, откуда чаще всего авторизуются в данной

социальную сети пользователь (может отсутствовать!)

Пример данных:

44053078 1166032023073 3067 1 10414533690 2423601 99

12495764 1177932393270 1138

2 10405172143 188081

25646929 1165304175170 3756 2 10414533690 3953941 22

25646999 1160728984480 3884 2 10414533690 241372 120

12495833 1176909723643 3363 2 10414533690 2724941 11

Демография партиционирована по той же схеме, что и граф, но не сжата (передается

в виде открытых текстов). Так же может быть обработана с помощью стандартного

инструмента хранения больших данных Apache Pig или любого другого инструмента,

поддерживающего CSV.

4.2 Формулировки задач

Задача 4.2.1 «Дата рождения»

Представленный для анализа фрагмент социального графа включает информацию о

связях 100 тысяч пользователей, попавших в двухшаговую окрестность сотни случайно

выбранных пользователей. Участникам предоставляются файлы графа социальной сети со

всеми связями и файл демографии, в котором указан данные по пользователям, включая

возраст, однако возраст указан не для всех пользователей.

По пользователям которые присутствуют в графе, но не присутствуют в демографии

необходимо установить значение их атрибута birth_date (дату рождения).

Данные записываются в файл в формате:

(\t(знак

продолжение следует...

Продолжение:

Часть 1 Машинное обучение на больших данных Теория и примеры решения задач
Часть 2 2.2. Критерии определения призеров и победителей - Машинное обучение на
Часть 3 4.3. Методика расчета баллов - Машинное обучение на больших данных