Алгоритм Шора

Привет, Вы узнаете о том , что такое алгоритм шора , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм шора , настоятельно рекомендую прочитать все из категории Квантовая информатика.

алгоритм шора  — квантовый алгоритм факторизации (разложения числа на простые множители), позволяющий разложить число  за время 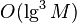, используя  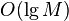логических кубитов.

Алгоритм Шора был разработан Питером Шором в 1994 году. Семь лет спустя, в 2001 году, его работоспособность была продемонстрирована группой специалистов IBM. Число 15 было разложено на множители 3 и 5 при помощи квантового компьютера с 7 кубитами.

 Питер Шор — автор алгоритма

Об алгоритме 

Значимость алгоритма заключается в том, что с его помощью (при использовании квантового компьютера с несколькими сотнями логических кубитов) становится возможным взлом криптографических систем с открытым ключом. К примеру, RSA использует открытый ключ , являющийся произведением двух больших простых чисел. Один из способов взломать шифр RSA — найти множители . При достаточно большом  это практически невозможно сделать, используя известные классические  алгоритмы . Наилучший из известных классических алгоритмов факторизации требует времени порядка 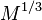. Алгоритм Шора, используя возможности квантовых компьютеров, способен произвести факторизацию числа не просто за полиномиальное время, а за время, не намного превосходящее время умножения целых чисел (то есть практически так же быстро, как происходит само шифрование). Таким образом, реализация масштабируемого квантового компьютера поставила бы крест на большей части современной криптографической защиты. ( Речь не только о схеме RSA, прямо опирающейся на сложности факторизации, но и о других сходных схемах, которые квантовый компьютер способен взломать аналогичным образом).

Алгоритм Шора имеет вероятностный характер . Первый источник случайности встроен в классическое вероятностное сведение разложения на множители к нахождению периода некоторой функции. Второй источник появляется из необходимости наблюдения квантовой памяти, которое также дает случайные результаты^[1].

Принцип работы алгоритма Шора 

Основа Алгоритма Шора: способность информационных единиц квантовых компьютеров — кубитов — принимать несколько значений одновременно и находиться в состоянии «запутанности». Поэтому он позволяет проводить вычисления в условиях экономии кубитов. Принцип работы алгоритма Шора можно разделить на 2 части: первая — классическое сведение разложения на множители к нахождению периода некоторой функции, вторая — квантовое нахождение периода этой функции. Пусть:

 — число, не являющееся корнем нечетного числа, которое хотим разложить на множители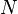

 — размер регистра памяти, который используется (не считая свалки)

Битовый размер этой памяти 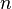 примерно в 2 раза больше размера .

Точнее,

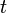 — случайный параметр, такой что  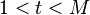и 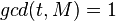,  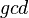— наибольший общий делитель.

Отметим, что 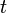, , 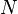 — фиксированы. В алгоритме Шора используется стандартный способ сведения задачи разложения к задаче поиска периода функции для случайно подобранного числа 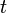^[2].

Классический алгоритм 

Минимальное  такое, что 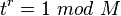 — это порядок  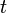по модулю .

Порядок  является периодом функции 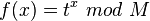, где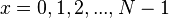 

Если можно эффективно вычислить  как функцию 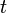, то можно найти собственный делитель  за время, ограниченное полиномом от 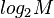 с вероятностью  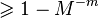для любого фиксированного .

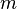Предположим, что для данного 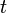 период  удовлетворяет

.

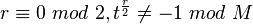Тогда

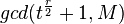 — собственный делитель . Об этом говорит сайт https://intellect.icu . Функция 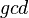 вычислима за полиномиальное время .

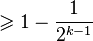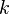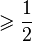Вероятность выполнения этого условия , где  — число различных нечетных простых делителей , следовательно,  в данном случае. Поэтому хорошее значение 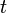с вероятностью  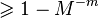найдется за  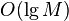попыток. Самое длинное вычисление в одной попытке — вычисление 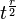^[3][4].

Квантовый алгоритм  

Для осуществления квантовой части алгоритма вычислительная схема представляет собой 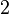 квантовых регистра  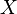и 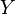. Первоначально каждый из них состоит из совокупности кубитов в нулевом булевом состоянии .

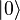Регистр 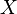 используется для размещения аргументов  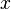функции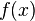 

Регистр 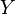 (вспомогательный) используется для размещения значений функции  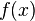с периодом , подлежащим вычислению.

Квантовое вычисление состоит из 4 шагов^[5]:

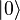• Первый шаг. На первом шаге с помощью операции Уолша-Адамара первоначальное состояние  регистра  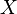переводится в равновероятную суперпозицию всех булевых состояний 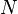. Второй регистр  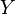остается в состоянии 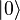. В итоге получается следующее состояние для системы двух регистров:

  

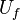• Второй шаг. Пусть  — унитарное преобразование, которое переводит  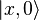в 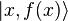. На втором шаге применяется унитарное преобразование к системе двух регистров. Получается следующее состояние системы :

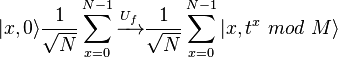, то есть между состояниями обоих регистров образуется определенная связь.

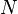• Третий шаг. Квантовое Фурье-преобразование представляет собой унитарное преобразование состояния квантового регистра, описываемого  — мерным вектором состояния вида  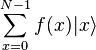в другое состояние :

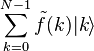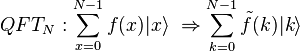, где амплитуда Фурье-преобразования  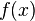имеет вид

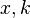В двумерной - плоскости преобразование Фурье соответствует повороту осей координат на 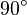, которое приводит к преобразованию шкалы  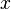в шкалу 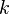. На третьем шаге над состоянием первого регистра производится преобразование Фурье, и получается

.

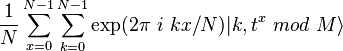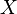• Четвертый шаг. На четвертом шаге выполняется измерение первого регистра  относительно ортогональной проекции вида:

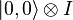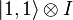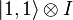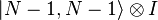, , , … ,, где 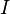 — тождественный оператор  на Гильбертовом пространстве второго регистра .

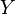В результате получается 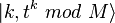 с вероятностью

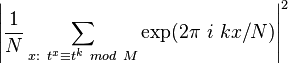^[6]

На оставшейся части прогона работает классический компьютер:

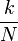• Находится наилучшее приближение (снизу) к  со знаменателем :

  

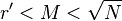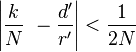
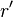• Пробуем  в роли :
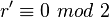  • Если , то следует вычислить .
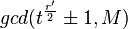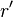  • Если  нечетно или если  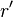четно, но собственный делитель  не обнаружен, то следует повторить прогон 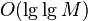 раз с тем же самым 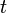. В случае отказа изменить  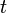и начать новый прогон алгоритма^[3][4].

В некоторой степени определение периода функции с помощью преобразования Фурье аналогично измерению постоянных решетки кристалла методом рентгеновской или нейтронной дифракции. Чтобы определить период  не требуется вычислять все значения 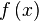. В этом смысле задача похожа назадачу Дойча, в которой знать важно не все значения функции, а только некоторые ее свойства^[6].

Нахождение периода функции в алгоритме 

Пусть 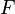 — функция с неизвестным периодом .

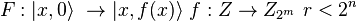
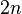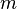Чтобы определить период  требуются два регистра с размерами  и  кубитов, которые в первоначальном состоянии должны быть в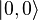 

На первом этапе выполняется односторонняя суперпозиция всех базисных векторов первого регистра с использованием оператора 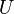 следующего вида:

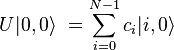, где  и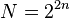 

Здесь используется псевдопреобразование Адамара 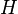. Применяя  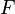к текущему состоянию получается:

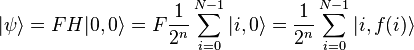
Измерение второго регистра с результатом 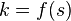, где 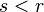 приводит состояние к

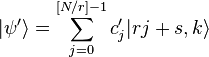 где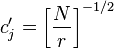 

После измерения состояния  первый регистр состоит только из базисных векторов вида 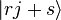 таких, что  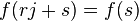для всех . Поэтому он имеет дискретный однородный спектр. Невозможно прямо получить период   или кратное ему число , измеряя первый регистр, потому что здесь  — случайная величина . Здесь применяется  дискретное преобразование Фурье  вида

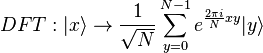 на регистр, так как вероятность спектра в преобразованном состоянии инвариантна относительно смещения (преобразованию поддаются только фазы, а не абсолютные значения амплитуд).

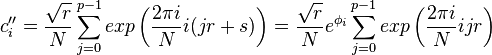
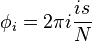где  и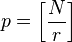 

Если 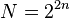 кратно , тогда 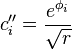, если  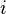кратно 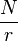, и 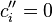 в противном случае. Даже если  не является степенью числа 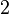, то спектр 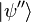показывает отдельные пики с периодом 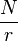, потому что

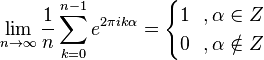
Для первого регистра используется 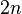 кубитов, когда , потому что это гарантирует по крайней мере 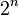 элементов в приведенной сумме, и таким образом ширина пиков будет порядка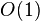 

Если теперь вычислить первый регистр, то получится значение  близкое к 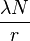, где . Оно может быть записано как 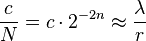 Это сводится к нахождению аппроксимации 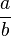, где 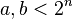, для конкретного числа двоичной точки  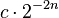Для решения этой проблемы используются цепные дроби.

Так как форма рационального числа не единственна в своем роде, то 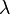 и  определяются как 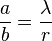, если  Вероятность того, что 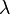 и просты, больше чем , таким образом только  попыток необходимо, чтобы вероятность успеха как можно ближе была к 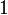^[7][5].

Выводы из данной статьи про алгоритм шора указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритм шора и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квантовая информатика