Алгоритм Дойча — Йожи кратко

Привет, Вы узнаете о том , что такое алгоритм дойча , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм дойча , йожи , настоятельно рекомендую прочитать все из категории Квантовая информатика.

алгоритм дойча — йожи (упоминается также как алгоритм Дойча — Джозы) —квантовый алгоритм, предложенный Давидом Дойчем и Ричардом Йожей[en] в 1992 году, и ставший одним из первых примеров алгоритмов, предназначенных для выполнения наквантовых компьютерах. Эти алгоритмы благодаря использованию явления квантовой запутанности и принципа суперпозиции обладают значительным приростом скорости выполнения по сравнению с соответствующими классическими алгоритмами.

Задача Дойча — Йожи заключается в определении является ли функция двоичной переменной 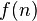постоянной (принимает либо значение 0, либо 1 при любых аргументах) или сбалансированной (для половины области определения принимает значение 0, для другой половины 1). При этом считается априорно известным, что функция либо является константой, либо сбалансирована.

Для решения этой задачи классическому детерминированному алгоритму необходимо произвести 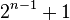вычислений функции f в худшем случае. Классическому вероятностному алгоритму потребуется меньше времени, чтобы дать верный ответ с высокой вероятностью. Но в любом случае для получения верного ответа с единичной вероятностью потребуется 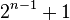вычислений. Алгоритм дает верный ответ, один раз применив фазовый запрос, соответствующий заданной функции f.

Если функция 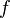несбалансирована, то алгоритм может выдать ответ «константа» с некоторой вероятностью, причем чем больше разница между количеством «0» и «1», тем больше будет эта вероятность[1].

Алгоритм Дойча — Йожи основан на разработанном Давидом Дойчем в 1985 году схожем алгоритме, являющемся частным случаем первого. В этом алгоритме функция 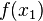являлась функцией одной переменной, в отличие от функции многих переменных 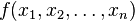, используемой в более позднем алгоритме.

Алгоритм

На входе алгоритма есть булева функция 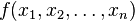от 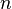булевых переменных. Алгоритм представляет собой применение к нулевому вектору 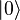оператора 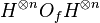и измерение состояния регистра. Об этом говорит сайт https://intellect.icu . Если все биты регистра равны 0, значит значение функции 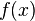не зависит от 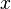, в противном случае функция является сбалансированной.

Здесь 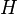— преобразование Адамара: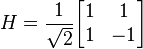

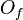— фазовый запрос, который инвертирует фазу для состояний регистра, соответствующих единицам функции 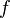и не изменяет состояния, соответствующие нулям функции: 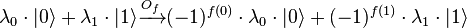[2]

Работа алгоритма на примере задачи Дойча

На вход алгоритму подается булева функция одной переменной 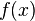. Всего существуют 4 такие функции[2]:

№	f(0)	f(1)
1	0	0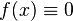
2	1	1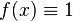
3	0	1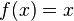
4	1	0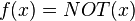

Функции 1 и 2 назовем константными, а функции 3 и 4 — сбалансированными.

На первом шаге задаем кубиту нулевое состояние: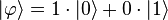

Применяя преобразование Адамара получаем 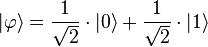. В принципе, можно было бы сразу назначить кубиту такое состояние, но технически проще сначала задать нулевое состояние, а потом преобразовать его с помощью унитарных преобразований к нужному виду.

Применяя фазовый запрос 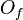к нашей функции 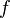, получаем следующее состояние: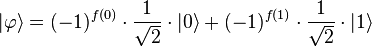

Второе преобразование Адамара приводит к следующему состоянию: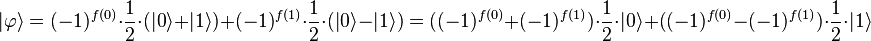

При измерении состояния кубита получим 0 для константных функций и 1 для сбалансированных. Это можно увидеть, если подставить всевозможные функции f(x) в выражение для состояния кубита:

№	f(0)	f(1)	Состояние кубита	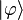Вероятность получения 0	Вероятность получения 1
1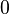
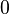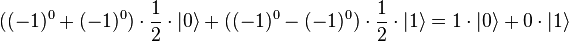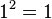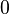2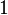
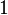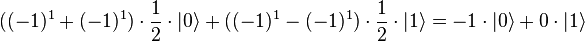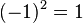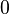3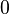
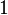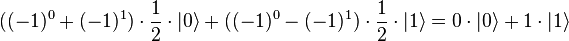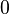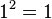4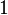

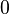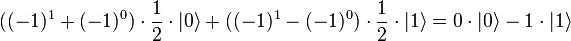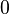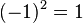Примечания

1. ↑ М. Вялый, Квантовые алгоритмы, лекция 2.
2. ↑ Перейти к:1 2 Квантовые алгоритмы: возможности и ограничения. М. Вялый, лекция 2, стр 12-13 (Санкт-Петербург, весна 2011)

Выводы из данной статьи про алгоритм дойча указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритм дойча , йожи и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квантовая информатика