Обратимая машина Тьюринга кратко

Привет, Вы узнаете о том , что такое обратимая машина тьюринга, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое обратимая машина тьюринга , настоятельно рекомендую прочитать все из категории Квантовая информатика.

обратимая машина тьюринга ( англ . Reversible Turing machine ) - это машина Тьюринга, в которой все возможные операции являются обратимыми . В результате вычисления, которые он производит, обратимы .

Будет описан способ строительства. Машина Тьюринга, которая в обычном случае является предметом многих дискуссий, имеет решающее значение. То есть для набора (q, s) состояния q и символа в позиции заголовка на ленте (далее просто называемого «символом») s. Есть только одно действие. В это время, если можно определить, какая операция была выполнена немедленно, глядя только на состояние и символ сразу после операции, машина Тьюринга может двигаться в противоположном направлении. Другими словами, именно обратимая машина тулинга «решает в обратном направлении».

Немного более формально (я обычно использую набор из 5 частей для формального описания машины Тьюринга, но здесь я использую модифицированный набор из 4 частей для удобства).

• [Q, /, d, q '] - это правило, согласно которому, когда состояние q является произвольным символом, он переходит в состояние q' и перемещается в направлении d без перезаписи символа.
• В случае символа s состояния q, правило перехода в состояние q 'и перезаписи символа на s' без перемещения определяется как .

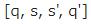Любые не те два правила [q из всех правил машины Тьюринга и

• Решающее значение имеет выборочная машина, где q ₁ = q ₂ и (b ₁ = b ₂ или b ₁ / или b ₂ /) никогда не выполняется.
• Кроме того, q ' ₁ = q' ₂ и (c ₁ = c ₂ или b ₁ / или b ₂ /) не установлено, машина Тьюринга обратима.

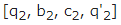
Реверсивный машин Тьюринга, все инъекции в вычислимой функции можно вычислить.

Машина Тьюринга называется обратимой , если у нее нет сливающихся достижимых ситуаций, и вполн е обратимой , если у нее нет никаких сливающихся ситуаций. Об этом говорит сайт https://intellect.icu . Вопрос о существовании обратимой и вполне обратимой машины Тьюринга, эквивалентной данной машине Тьюринга, рассматривался В. С. Чернявским Он назвал эквивалентным и относительно алфавита 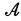такие машины Тьюринга, которые, начав работу с одной и той же начальной ситуации в алфавите м, дают одну и ту же заключительную ситуацию всякий раз, когда одна из них дает какую-нибудь заключительную ситуацию.

В. С. Чернявским доказано, что для всякой машины Тьюринга Т в алфавите 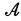существует обратимая машина Тьюринга, эквивалентная машине Т относительно алфавита 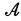, для всякой машины Тьюринга Т существует эквивалентная ей относительно ее алфавита машина, являющаяся композицией трех вполне обратимых машин.

Машины Тьюринга мы будем называть вполн е эквивалент ­ ным и относительно алфавита 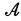, если, начав работу с одной и той же q₁-ситуации в алфавите 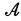, они дают одну и ту же заключительную ситуацию всякий раз, когда одна из них дает какую-нибудь заключительную ситуацию. Очевидно, что если машины вполне эквивалентны относительно алфавита 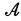, то они эквивалентны относительно этого алфавита.

Теорема 1. Для всякой машины Тьюринга Т в алфавите 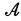можно построить вполне обратимую машину Т^-1 такую, что для любых q₁-ситуаций Сг и заключительной ситуации C₀ машины Т ситуация C₀ достижима из -С₁ в машине Т тогда и только тогда, когда ситуация С₁ достижима из C₀ в машине Т^-1 .

Теорема 2. Для всякой машины Тьюринга Т в алфавите 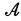можно построить вполне обратимую машину Т*, вполне эквивалентную машине Т - относительно алфавита .

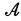Теорема 2 является усилением указанных выше результатов В. С. Чернявского.

Основные черты доказательства теорем 1 и 2 состоят в следующем. По данной машине Т в алфавите 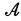строится вспомогательная машина Т₄ в этом алфавите, вполне эквивалентная машине Т относительно 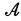и обладающая следующими свойствами:

а) все состояния односторонни и не более двух команд могут иметь одинаковые правые части;

b) всякая q₁-ситуация элементарно недостижима, и q₁-ситуация, к которой машина Т₄ применима, является неодинокой;

с) всякая ситуация, к которой машина Т₄ применима, шли элементарно недостижима, или есть кратная, или есть неодинокая.

Из свойства а) машины Т₄ следует, что у машины Т₄ каждая ситуация достижима не более чем из двух ситуаций. Для каждой пары команд машины Т₄ с общей правой частью договоримся раз и навсегда называть одну из них d-командой, а другую — b-командой. Пусть 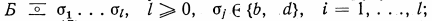. тогда выражение 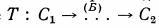обозначает, что в последовательности ситуаций 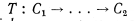порядок употребления 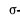-команд, где 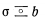или 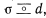, таков: 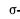₁-команда, 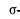₂-команда, . . ., 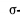_i -команда.

Литература

Вау!! 😲 Ты еще не читал? Это зря!

• Машина Тьюринга
• Обратимые вычисления
• Обратимая архитектура процессора
• Обратимые логические схемы: Тоффоли (1980-е).
• Обратимые классы сложности : 1990-е

Исследование, описанное в статье про обратимая машина тьюринга, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое обратимая машина тьюринга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квантовая информатика