Алгоритм Гровера кратко

Привет, Вы узнаете о том , что такое алгоритм гровера , Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое алгоритм гровера , настоятельно рекомендую прочитать все из категории Квантовая информатика.

алгоритм гровера (англ. Grover search algorithm, GSA) — квантовый алгоритм решения задачи перебора, то есть нахождения решения уравнения

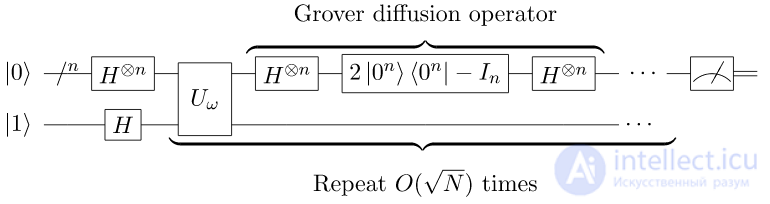
Алгоритм Гровера

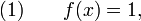
где 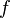есть булева функция от n переменных.[1]

Предполагается, что функция 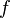задана в виде черного ящика, или оракула, то есть в ходе решения мы можем только задавать оракулу вопрос типа: «чему равна 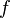на данном 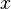», и после получения ответа использовать его в дальнейших вычислениях. То есть задача решения уравнения (1) является общей формой задачи перебора; здесь требуется отыскать «пароль к устройству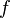», что классически требует прямого перебора всех 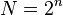вариантов.

GSA находит какой-нибудь корень уравнения, используя 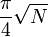обращений к функции 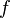, с использованием 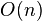кубитов.[2] Алгоритм был открыт американским математиком Ловом Гровером в 1996 году.

Реальная интерпритация, перед вами четыре игральные карты. Они повернуты рубашками вверх. Вы знаете, что одна из них — туз червей и вам нужно найти ее. Сколько карт придется перевернуть, пока вы не узнаете, где лежит туз червей?

Если вам повезет, вы найдете искомую карту с первой же попытки, если не повезет, вы можете перевернуть три карты, и ни одна из них не будет тузом червей. В худшем случае, перевернув три карты, вы будете точно знать, что последняя карта — это искомый туз червей. Итак, мы можем узнать, где находится туз, перевернув от одной до трех карт. В среднем понадобится перевернуть 2,25 карты.

Это одна из задач, которые решает алгоритм Гровера. Перед началом описания алгоритма переформулируем задачу. У нас есть четыре двоичные последовательности: 00, 01, 10 и 11. У нас есть функция f, которая возвращает 0 для трех из этих последовательностей и 1 — для четвертой последовательности. Нам нужно найти двоичную последовательность, соответствующую выходному значению 1. Например, мы можем получить такие результаты: f(00) = 0, f(01) = 0, f(10) = 1 и f(11) = 0. Теперь задача состоит в том, чтобы выяснить, сколько раз следует вычислить функцию, чтобы получить результат f(10) = 1. Здесь мы просто переформулировали задачу, заменив игральные карты функциями, поэтому ответ на этот вопрос уже известен: как и прежде, в среднем потребуется вычислить функцию 2,25 раза.

Свойства

Если уравнение (1) имеет корней, по схеме Гровера можно найти один из них на квантовом компьютере за время 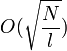(даже если 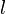не известно заранее), то есть основная квантовая сложность является квадратным корнем из классической.

Классический алгоритм решения такой задачи (линейный поиск), очевидно, требует 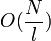обращений к 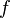. Об этом говорит сайт https://intellect.icu . Алгоритм Гровера позволяет решить задачу поиска за время порядка квадратного корня из классического, что является огромным ускорением. Доказано, что GSA является оптимальным в следующих отношениях:

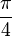• Константу нельзя улучшить [3].
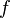• Большего квантового ускорения, чем квадратичное, нельзя получить для неисчезающей доли всех возможных черных ящиков [4].

GSA есть пример массовой задачи, зависящей от оракула. Для более частных задач удается получить большее квантовое ускорение. Например, алгоритм факторизации Шора дает экспоненциальный выигрыш по сравнению с соответствующими классическими алгоритмами.

То, что f задана в виде черного ящика, никак не влияет в общем случае на сложность как квантовых, так и классических алгоритмов. Знание «устройства» функции f (например, знание задающей ее схемы из функциональных элементов) в общем случае никак не может помочь в решении уравнения (1). Поиск в базе данных соотносится с обращением функции, которая принимает определенное значение, если аргумент x соответствует искомой записи в базе данных.

Пусть 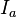есть унитарный оператор, зеркально отражающий гильбертово пространство относительно гиперплоскости, перпендикулярной вектору 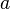, 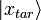— состояние, соответствующее корню уравнения (1), 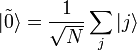— равномерная суперпозиция всех состояний. Тогда GSA состоит в применении оператора 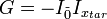к состоянию число раз, равное целой части 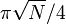. Результат будет почти совпадать с состоянием .

Алгоритмы, использующие схему Гровера

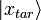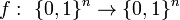• Алгоритм поиска экстремума целочисленной функции (P. Hoyer и др.). Ищется наибольшее значение функции . Квантовый алгоритм находит максимум за 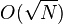обращений к f.
• Алгоритм структурного поиска (Farhi, Gutman). Ищется решение уравнения (1) при дополнительном условии , где 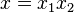разбиение строки 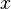на две строки одинаковой длины. Алгоритм имеет сложность порядка квадратного корня из классического времени.
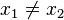• Алгоритм поиска совпадающих строк в базе данных (Амбайнис). Ищется пара разных аргументов , на которых функция 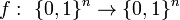принимает одно и то же значение. Алгоритм требует 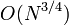обращений к f.

Непрерывные версии алгоритма Гровера

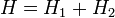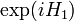• Пусть гамильтониан квантовой системы имеет вид , где и 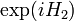представляют собой операторы 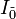и 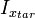соответственно. Тогда непрерывная унитарная эволюция с гамильтонианом 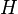, стартуя с , естественно приводит к 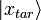. Сложность такого непрерывного аналога GSA точно та же, что и для дискретного случая.
• Адиабатический вариант GSA. Медленная эволюция основного состояния типа под действием гамильтониана, зависящего от f, согласно адиабатической теореме, за время порядка 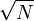ведет к состоянию .

Применение

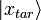Смысл GSA состоит в «подскоке амплитуды» (amplitude amplification) целевого состояния за счет убывания амплитуды всех других состояний. Геометрически GSA заключается во вращении текущего вектора состояния квантового компьютера по направлению точно к целевому состоянию (движение по наикратчайшему пути обеспечивает оптимальность GSA). Каждый шаг дает вращение на угол 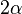, где угол между 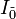и 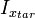составляет 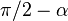. Дальнейшее продолжение итераций оператора G даст продолжение обхода окружности в вещественной плоскости, порожденной данными векторами.

Гроверовский «подскок амплитуды» является, по-видимому, фундаментальным физическим феноменом в квантовой теории многих тел. Например, его учет необходим для оценки вероятностей событий, которые кажутся «редкими». Процесс, реализующий схему GSA, приводит к взрывному росту первоначально пренебрежимо малой амплитуды, что способно быстро довести ее до реально наблюдаемых величин.

Алгоритм Гровера также может быть использован для нахождения медианы и среднего арифметического числового ряда. Кроме того, он может применяться для решения NP-полных задач путем исчерпывающего поиска среди множества возможных решений. Это может повлечь значительный прирост скорости по сравнению с классическими алгоритмами, хотя и не предоставляя «полиномиального решения» в общем виде.

С реализацией алгоритма связано несколько проблем. Во-первых, квадратичное ускорение оценивается относительно запроса сложности. Чтобы использовать оракула, его нужно создать, и если не отнестись с к этой задаче с должной осторожностью, число шагов, выполняемых оракулом, перевесит число шагов, которое экономит алгоритм, и в результате алгоритм станет медленнее, а не быстрее классического. Другая проблема состоит в том, что, определяя ускорение, мы предполагаем неупорядоченность набора данных. Если набор данных имеет определенную структуру, часто можно найти классический алгоритм, использующий эту структуру и отыскивающий решение намного быстрее. Последняя проблема связана с ускорением. Квадратичное ускорение — не что иное, как экспоненциальное ускорение, которое мы наблюдали в других алгоритмах. Можно ли добиться большего? Давайте рассмотрим эти проблемы.

Обе проблемы, связанные с реализацией оракула и наличием структуры в наборе данных, обоснованы и показывают, что в большинстве случаев алгоритм Гровера не имеет практического применения для поиска в базе данных. Но в некоторых ситуациях наличие структуры в данных делает возможным создание оракула, действующего с высокой эффективностью. В таких ситуациях алгоритм может обогнать классические алгоритмы. Ответ на вопрос о возможности добиться большего успеха уже был дан. Доказано, что алгоритм Гровера является оптимальным. Не существует квантового алгоритма, способного решить задачу с более чем квадратичным ускорением. Квадратичное ускорение, хотя и не такое впечатляющее, как экспоненциальное, все еще дает определенные выгоды. При работе с большими наборами данных любое ускорение может оказаться ценным.

Вероятно, главное применение алгоритм Гровера найдет не для поиска, как было представлено выше, а для его вариаций. В частности, может пригодиться идея усиления амплитуды.

Вау!! 😲 Ты еще не читал? Это зря!

• Квантовый компьютер

Примечания

1. ↑ Иногда GSA неточно называют поиском в базе данных.
2. ↑ Сложность работы алгоритма, для задачи с оракулом называемая еще временем его работы, определяется числом обращений к оракулу.
3. ↑ Christof Zalka, Grover’s quantum searching algorithm is optimal, Phys.Rev. A60 (1999) 2746—2751 [1]
4. ↑ Yuri Ozhigov, Lower Bounds of Quantum Search for Extreme Point, Proc.Roy.Soc.Lond. A455 (1999) 2165—2172 [2]

Ссылки

• Гровер Л. К. Квантовая механика помогает найти иголку в стоге сена (для скачивания)
• Логинов О. В. и Цыганов А. В. Квантовый алгоритм Гровера, Санкт-Петербургский Государственный Университет
• Исходные тексты симулятора квантового компьютера на C++ и реализации алгоритма Гровера с подробным описанием и схемами квантовых вентилей

Выводы из данной статьи про алгоритм гровера указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое алгоритм гровера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квантовая информатика