Основные определения, связанные со строками.Строковые алгоритмы кратко

Привет, Вы узнаете о том , что такое строковые алгоритмы, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое строковые алгоритмы, префикс , суффикс , бордер , период , подстрока , палиндромом , настоятельно рекомендую прочитать все из категории Компьютерная лингвистика.

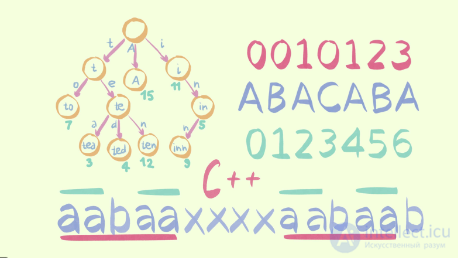
Автоматизированная обработка текстов не теряет своей актуальности. Потребность в ней возникает как при решении простейших прикладных задач, так и в активно развивающихся областях науки, таких как генетика. Анализ цепочек ДНК, разработка компиляторов, реализация полнотекстового поиска в СУБД, словарные методы сжатия данных и, наконец, небольшие программы для банального редактирования описаний товаров в базе данных – всѐ это области применения строковых алгоритмов. Прежде всего, следует определить основные термины, использующиеся в этом разделе. Символ в данном случае весьма широкое понятие – это информационная единица, определенного типа, которой, как правило, сопоставляется некая печатная форма.

Базовые определения

Алфавит –.Алфавит (англ. alphabet) — конечное непустое множество символов. Условимся обозначать алфавит большой греческой буквой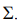

Наиболее часто используются следующие алфавиты:

• Σ={0,1} — бинарный или двоичный алфавит.
• Σ={a,b,…,z} — множество строчных букв английского алфавита.
• Σ={0,1,2,…,9} — алфавит цифр.
• Σ={⋅,−} — алфавит, лежащий в основе азбуки Морзе.
• Нотные знаки

Символ (англ. symbol) — объект, имеющий собственное содержание и уникальную читаемую форму.

Строка (слово) – последовательность символов некоторого алфавита.

Длина строки – количество символов в строке. Длина цепочки (англ. string length) — число символов в цепочке. Длину некоторой цепочки ww обычно обозначают |w||w|.

Строку обозначают символами алфавита, например 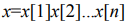– строка длиной n, где x[i] – i -ый символ. Длину строки x обычно обозначают |x|.

Σk — множество цепочек длины k над алфавитом Σ .

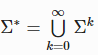— множество всех цепочек над алфавитом Σ .

Конкатенация – сцепление, операция «склеивания» строк. Конкатенацию строк x и y обозначают xy.

Пусть 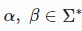. Тогда α⋅β или αβ обозначает их конкатенацию (англ. concatenation), то есть цепочку, в которой последовательно записаны цепочки α и β .

Пустая строка – строка, не содержащая ни одного символа. Пустая цепочка (англ. empty string) — цепочка, не содержащая ни одного символа. Эту цепочку, обозначаемую ε , можно рассматривать как цепочку в любом алфавите. Для любой строки 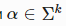верно : .

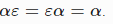Множество строк с операцией конкатенации и нейтральным элементом пустой строкой образует свободный моноид.

подстрока – некоторая непустая последовательность идущих подряд символов строки. Строка x называется подстрокой строки y, если найдутся такие
строки z1 и z2, что .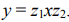

префикс – некоторое начало строки. Префикс p строки t – строка такая, что pv=t для некоторой (возможно, пустой) строки v. Префикс называется
собственным, если .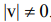

суффикс – некоторое окончание строки. Суффикс s строки t – строка такая, что vs=t для некоторой (возможно, пустой) строки v. Суффикс называется
собственным, если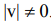

Отношения между строками

Определение: Префикс (англ. Об этом говорит сайт https://intellect.icu . prefix) строки β — строка α:β=αγ

Пусть 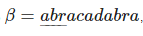, тогда α=abr — префикс β .

Определение: Суффикс (англ. suffix) строки ββ — строка α:β=γα .

Пусть β= 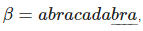, тогда α=bra — суффикс β.

Определение: бордер (англ. circumfix) строки β — строка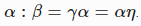

Пусть 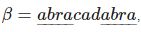, тогда α=abra — бордер β.

Определение: α[i] — символ строки α, находящийся на i-ой позиции.

Пусть 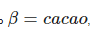, тогда .

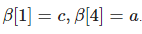Определение: период (англ. period) строки αα — число .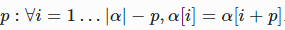

Пусть 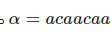, тогда p=3 — период строки α=acaacaa .

Утверждение:

Пусть известна строка ττ — период αα и |α||α|, тогда можно восстановить всю строку αα.

Из определения периода строки следует, что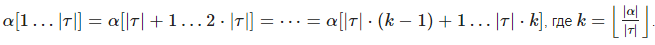

Таким образом .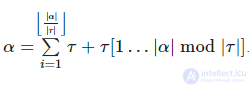

Определение: Строка α≠ε c периодом p≠|α| , называется сильнопериодической, если |α|modp=0 .

Строка α=acaacaaca является сильнопериодической с периодом p=3

Определение: Подстрока (англ. substring) — некоторая непустая подпоследовательность подряд идущих символов строки.

Пусть 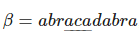тогда α=aca — подстрока строки β.

Определение: Тандемным повтором (англ. repetition) называется непустая строка вида αα .

Определение: палиндромом (англ. Palindrome) называется строка вида 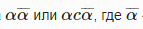— развернутая строка α, c — любой символ.

Определение: Строка α лексикографически меньше строки β (α<β ), если

1. α — префикс β

или

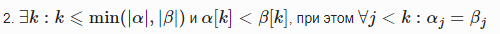
Строка α=aca<β=acaaba , так как является префиксом β.

Строка α=acaa<β=acab , так как a

Формальные языки

Определение: Язык (англ. language) над алфавитом Σ — некоторое подмножество Σ∗ . Иногда такие языки называют формальными (англ. formal), чтобы подчеркнуть отличие от языков в привычном смысле.

Отметим, что язык в Σ не обязательно должен содержать цепочки, в которые входят все символы Σ. Поэтому, если известно, что L является языком над Σ, то можно утверждать, что L — это язык над любым алфавитом, являющимся надмножеством Σ.

Операции над языками

Пусть L и M — языки. Тогда над ними можно определить следующие операции.

1. Теоретико-множественные операции:
   • L∪M — объединение,
   • L∩ML — пересечение,
   • L∖M — разность,
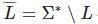   • — дополнение.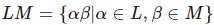
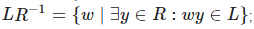2. Конкатенация:
3. Конкатенация с обратным языком: ; конкатенация с обратным словом: .
4. Степень языка: .
5. Замыкание Клини: .
6. Гомоморфизм

Примеры

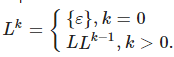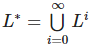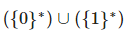• — язык состоит из последовательностей нулей, последовательностей единиц и пустой строки.
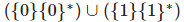• — аналогично предыдущему, но не содержит пустую строку.
• — содержит все двоичные векторы и пустую строку.
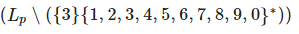• Если Lp — язык десятичных представлений всех простых чисел, то язык будет содержать десятичные представления простых чисел, не начинающихся с тройки.
• .

Гомоморфизм языков

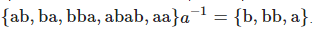Определение: Пусть даны два алфавита Σ1,Σ2 . Гомоморфизмом называется такое отображение 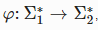, что:

• φ(ε)=ε , то есть сохраняет пустую строку
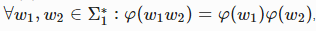• , то есть сохраняет конкатенацию

Определение:

Образом языка L⊂Σ∗1 при гомоморфизме φ:Σ∗1→Σ∗2 (иногда называют прямым гомоморфизмом) называется язык

.
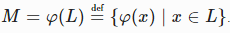Заметим, что φφ будет гомоморфизмом моноидов ⟨L,⋅,ε⟩ и ⟨M,⋅,ε⟩

Определение: Прообразом языка M⊂Σ∗2M⊂Σ2∗ при гомоморфизме φ:Σ∗1→Σ∗2 (иногда называют обратным гомоморфизмом) называется язык
Заметим, что φφ будет гомоморфизмом моноидов ⟨L,⋅,ε⟩ и ⟨M,⋅,ε⟩

Примеры

• тривиальные гомоморфизмы
  • обнуляющий: φ(x)=ε,x∈L , тогда φ(L)={ε}
  • тождественный: φ(x)=x,x∈L , тогда φ(L)=L и φ−1(L)=L
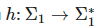• гомоморфизм цепочек — функция, подставляющая некоторую строку вместо каждого символа. Более формально, для заданного отображения гомоморфизмом цепочек будет функция φ:Σ∗1→Σ∗2 , действующая от каждого символа строки из языка следующим образом . Регулярные языки замкнуты относительно гомоморфизма цепочек
• солнечный язык из детских игр (когда после каждой гласной в слове надо добавлять букву "С" и эту же гласную) может быть представлен в виде гомоморфизма языков, где все согласные символы отображаются сами в себя, а гласный символ z переходит в zCz
• циклический гомоморфизм: зафиксируем порядок символов в алфавите, будем отображать каждый символ в следующий, а последний — в первый. Обратным гомоморфизмом будет отображение каждого символа в предыдущий.

Основные определения. Простые комбинаторные свойства слов

• Основные определения, связанные со строками
• Период и бордер, их связь
• Слово Фибоначчи
• Слово Туэ-Морса
• Декомпозиция Линдона
• Алгоритм Ландау-Шмидта
• Алгоритм Крочемора
• Алгоритм Мейна-Лоренца
• Алгоритм Манакера
• Дерево палиндромов

строковые алгоритмы - Поиск подстроки в строке

Точный поиск

• Наивный алгоритм поиска подстроки в строке
• Поиск подстроки в строке с использованием хеширования. Алгоритм Рабина-Карпа
• Поиск наибольшей общей подстроки двух строк с использованием хеширования
• Префикс-функция
• Алгоритм Кнута-Морриса-Пратта
• Автомат Кнута-Морриса-Пратта
• Z-функция
• Бор
• Алгоритм Ахо-Корасик
• Суффиксный автомат
• Алгоритм Бойера-Мура
• Алгоритм Апостолико-Крочемора
• Алгоритм Колусси
• Алгоритм Райта
• Алгоритм Shift-And
• Двусторонний алгоритм
• Турбо-алгоритм Бойера-Мура

Нечеткий поиск

• Алгоритм Ландау-Вишкина (k несовпадений)
• Алгоритм Ландау-Вишкина (k различий)

Строковые алгоритмы - Суффиксное дерево

• Суффиксный бор
• Сжатое суффиксное дерево
• Алгоритм Укконена
• Алгоритм МакКрейта
• Алгоритм Фараха

Строковые алгоритмы - Суффиксный массив

• Суффиксный массив
• Построение суффиксного массива с помощью стандартных методов сортировки
• Алгоритм цифровой сортировки суффиксов циклической строки
• Алгоритм Касаи и др.
• Алгоритм Карккайнена-Сандерса
• Алгоритм поиска подстроки в строке с помощью суффиксного массива
• Количество подпалиндромов в строке

Вау!! 😲 Ты еще не читал? Это зря!

• Период и бордер , их связь
• Слово Фибоначчи
• Слово Туэ-Морса
• Регулярные языки: два определения и их эквивалентность

Исследование, описанное в статье про строковые алгоритмы, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое строковые алгоритмы, префикс , суффикс , бордер , период , подстрока , палиндромом и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная лингвистика