Период и бордер для строк, их связь кратко

Привет, Вы узнаете о том , что такое период, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое период, бордер , настоятельно рекомендую прочитать все из категории Компьютерная лингвистика.

Связь период а и бордер а

Теорема:

Если у строки длины n есть бордер длины k , то у нее также имеется период длины n−k .

Доказательство:

Пусть дана строка αα.

Напишем формально определение бордера длины kk строки αα:

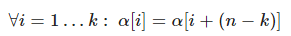
Сделаем замену x=n−k :

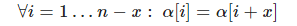
Получили определение периода длины x . Но x=n−k , значит у строки αα есть период длины n−k .

Свойства периода

Теорема (о кратном периоде):

Если у строки есть период длины k , то у нее имеется также период длины kx , где x∈N .

Доказательство:

Пусть длина строки равна nn, сама строка — α.

Доказательство будем вести индукцией по числу x.

• База

  Для x=1 утверждение очевидно.

• Переход

  Пусть верно для x⩽m. Докажем то же для x=m+1.

  Из определения периода имеем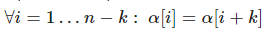

  

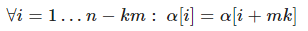
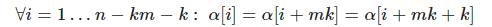
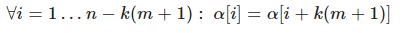
  а из предположения индукции

  

  С учетом этого получаем, что

  

  следовательно

  

  Значит у строки есть период длины k(m+1).

Утверждение доказано.

Перед доказательством следующей теоремы проверим пару интуитивно понятных утверждений.

Лемма (1):

Пусть строка ss имеет периоды p и q, причем q

Доказательство:

Покажем истинность утверждения про префикс; с суффиксом доказательство аналогичное.

Требуется показать: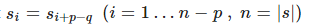

Исходя из того, что ss имеет период p , выполнено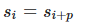

Также s имеет период q и из ограничений на ii верно , поэтому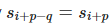

Лемма (2):

Пусть строка ww имеет период qq, и существует vv подстрока ww такая, что |v|⩾q|v|⩾q и vv имеет период rr, где qq ⋮⋮ rr. Об этом говорит сайт https://intellect.icu . Тогда ww имеет период rr.

Доказательство:

Пусть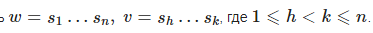

Требуется показать: .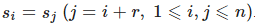

Зафиксируем ii и jj. Заметим, что поскольку |v|⩾q|v|⩾q, отрезок [h,k][h,k] содержит по меньшей мере qq целых чисел, так что найдутся

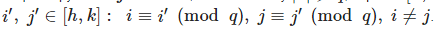j.

С учетом qq ⋮⋮ rr можем написать i≡i′(modr), j≡j′(modr)i≡i′(modr), j≡j′(modr) .

Помимо того i≡j(modr) , а в таком случае верно и i′≡j′(modr) .

Теперь воспользуемся следующим фактом: если строка ss имеет период rr, то i≡j(modr) ⇒ si=sj (действительно, без ограничения общности можем сказать, что i⩽ , и исходя из этого выстроить цепочку равенств si=si+r, si+r=si+2r, … , sj−r=s ).

В виду того, что ww имеет период qq, имеют место равенства si=si′ si=si′ и sj=sj′ sj=sj′. Кроме того vv имеет период rr, потому верно si′=sj′si′=sj′. Тогда и si=sjsi=sj.

Теорема (Фин и Вильф):

Если у строки ww есть периоды p и q , где 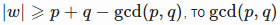также является периодом этой строки.

Доказательство:

Обозначим r=gcd(p,q) . Доказательство будем вести индукцией по n=(p+q)/r .

В случае p=q видим что n=2 , что соответствует базе, в то время как при p≠q выполнено max(p,q)>gcd(p,q) , так что n>2 .

• База

  Истинность утверждения следует из p=q=r .

• Переход

  В силу того, что p≠q , без ограничения общности будем считать q

  Пусть w=uv , где |u|=q .

  По лемме 1 vv имеет период p−qp−q, также vv имеет период qq как подстрока ww. Теперь рассмотрим длину vv:

  

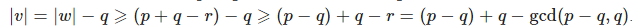
  Еще заметим, что для периодов p−q, q будет меньшее n , нежели чем для p, q , поскольку 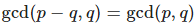. А тогда по предположению индукции заключаем: v имеет период 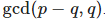Учитывая 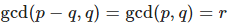, можем сказать что vv имеет период r.

  Как уже упоминалось, 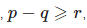, поэтому 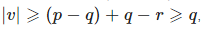, в следствие чего по лемме 2 ww имеет период rr.

Вау!! 😲 Ты еще не читал? Это зря!

• Основные определения, связанные со строками

Исследование, описанное в статье про период, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое период, бордер и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Компьютерная лингвистика

Из статьи мы узнали кратко, но содержательно про период