Лекция
Привет, Вы узнаете о том , что такое текстура, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое текстура, понятие «текстура» статистический подход к обработке текстурных изображений построение матрицы смежности , настоятельно рекомендую прочитать все из категории Методы и средства компьютерных информационных технологий.
1 Определение понятие текстура в системе распознавания образов и изображений
2 Статистический подход к описанию текстур
3 Дополнительные признаки, основанные на статистических характеристиках (матрицы смежности)
4 Структурный подход к описанию текстур
5 Фрактальный подход к описанию текстур
6 Оценка наличия текстуры в изображении
Пикетт дал такую формулировку: «текстура используется для описания двумерных массивов изменений яркости», Претт – «текстура – описание пространственной упорядоченности элементов изображения», Харалик – «текстура – организованный участок поверхности», Тамура – «текстура – нечто составляющее макроскопическую область», Ричардс – «текстура определена для наших целей как атрибут поля, не имеющего никаких компонентов (составляющих), которые выступают счетными (перечислимыми)» [2-4].
Известно, что текстура обладает рядом свойств. Именно благодаря этим свойствам можно с уверенностью говорить, что работа ведется с текстурой. Основные свойства текстур можно описать так:
текстура – свойство области; текстура точки не определена. Т.е. текстура – это контекстное свойство, и его определение должно включать в себя значенияуровней серого в окрестности. Размер этой окрестности зависит от типа текстуры
или размера примитивов (простых геометрических элементов изображения),определяющих текстуру;
- текстура в изображении может быть воспринята в различных масштабах или
уровнях разрешения;
- область воспринимается как текстурная, когда число элементарных объектов (примитивов) в области велико. Если только несколько элементарных объек- тов присутствуют, то воспринимается группа исчисляемых объектов вместо
текстурируемого изображения
Известны разные подходы к измерению и описанию текстуры изображения – статистические, геометрические, структурные
В первых работах по анализу текстур использовались такие признаки, как средняя оптическая плотность снимка и средняя пространственная частота [64].
Авторы работы [65] в качестве признаков при автоматической классификации аэрофотоизображений используют среднее значение оптической плотности и ее дисперсию. В работе [66] для автоматического анализа формы облачности применяются собственные векторы ковариационной матрицы яркостей элементов скользящего окна (прямоугольного фрагмента изображения) размером 6×6 элементов.
Распределение яркостей пар соседних элементов и двумерная aвтокорреляционная функция в качестве описания изображений облачных полей исследуются в работе [67]. В более поздних работах Розенфельд описывает текстуру плотностью перепадов яркости, то есть количеством перепадов яркости на единицу площади [68].
Харалик [69] для различения текстур использует ковариационные матрицы, характеризующие статистики второго порядка и описывающие пространственные связи пар яркостей элементов в цифровом изображении текстуры. Этот подход основан на предположении Юлеша [70] о том, что человеческий глаз использует статистики не выше второго порядка для
распознавания текстур. В 1978-1980 годах Юлеш и Гагалович [71, 72] посредством моделирования построили контрпримеры, состоящие однако из искусственных текстур, не встречающихся в природе. В работе [73]
элементы ковариационной матрицы B(i,j) являются счетчиками числа переходов яркости i в яркость j для пар элементов изображения, отстоящих на заданном расстоянии d. Эта характеристика не инвариантна к повороту, поэтому необходимо считать число переходов для каждого анализируемого направления.
Чаще используется не вычисление ковариационных матриц кактаковых, а оценка основанных на них признаков, характеризующих текстуру. В работе [69] Харалик предлагает использовать 14 признаков текстур, основанных на статистике и теории информации. В работе [73] на основе анализа этих признаков, авторами предложено использовать только 6 из них, представляющих оценку изображения по его информационным и статистическим характеристикам, таким как характеристика однородности, контраст, энтропия, количество информации. Для анализа текстур авторами работ [74 − 76] на основании теории статистического кодирования и данных физиологии зрения предлагается использовать распределение отрезков контуров и интервалов между контурными элементами. Эти характеристики можно измерять за время одного ТВ кадра посредством простых схем нелинейных фильтров, регистров сдвига и фильтров с обратной связью. При построении ТВ автомата, работающего в реальном времени [77], для классификации неоднородных текстур использовалась оценка максиминных расстояний между контурами.
Рассмотрим работу этого автомата подробнее. При создании автоматической системы для анализа неоднородных текстурных изображений выполняется следующая процедура. Анализируемое
изображение разбивается на фрагменты. Для каждого фрагмента оцениваются характеристики и строятся гистограммы их распределения. Отдельные информативные отсчеты полученных распределений выбираются в качестве признаков для распознавания. Параметры классификации такие, как размер фрагмента, количество уровней квантования гистограммы распределения признаков и количество информативных признаков, остаются неопределенными.
Для нахождения параметров используется метод «стабильности» моды. Для некоторого признака строится зависимость количества мод гистограммы от определяемого параметра. Наибольшая область этого параметра, в которой количество мод остается постоянным, называется зоной «стабильности» моды, а середину этой области используют в качестве значения неизвестного параметра. Если распределение какого-то признака не имеет мод или имеет только 1 моду, то признак считается неинформативным и отбрасывается.
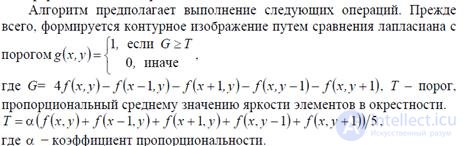
Подсчитывается число контурных элементов во фрагменте, получается достаточно эффективная характертеристика для
классификации некоторых изображений Оценивается распределение интервалов между контурами (внутри каждой строки при построчном сканировании изображения) по формуле:
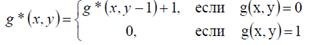


Для классификации выбран алгоритм самообучения, работающий по критерию минимальной ошибки классификации [78]. Исследования показали, что такие методы эффективно работают в задачах анализа 139
изображений, когда не предъявляется строгих требований к форме границы между статистически однородными областями. Использование оценки максиминных расстояний эффективнее оценки числа контурных элементов и оценки распределения интервалов между контурами. Для анализа анизотропных текстур предложены алгоритмы, учитывающие зависимости распределения интервалов между контурами и отрезков контуров вдоль направлений сканирования текстуры [49, 79].
Работы [62, 64-81] построены на статистическом подходе к описанию текстур. Об этом говорит сайт https://intellect.icu . При статистическом подходе к описанию текстур изображения трактуются как реализации некоторого случайного процесса. В работе [82] введено понятие типового изображения, порожденного эргодическим источником. Под текстурами понимают такие типы изображений, класс
которых обладает свойством эргодичности, то есть любое изображение данной текстуры является типовым и полностью характеризует все другие изображения, относящиеся к этому классу.
В качестве таких признаков можно использовать статистические моменты пространственных распределений, вычисляемые как меры однородности по одномерной гистограмме значений сигналов (характеристики 1-го порядка) и по двумерным гистограммам значений сигналов(характеристики 2-го порядка). Так, в качестве численных оценок текстуры по одномерной гистограмме можно использовать следующие статистические характеристики [5]:


Анализ показывает, что текстурные оценки (5)–(8), вычисляемые по одномерной гистограмме частот, не учитывают взаимного расположения соседних пикселей в скользящем окне и позволяют оценивать лишь групповые свойства пикселей, входящих в состав того или иного ландшафтного объекта на аэрокосмическом изображении. Таким образом, данные оценки эффективны лишь для описания текстур с невыраженной пространственной регулярностью.
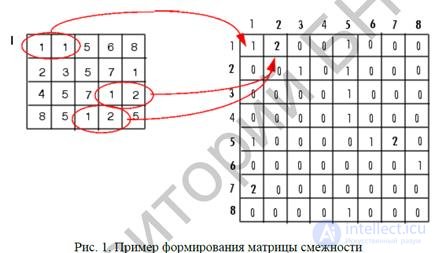
Для формирования текстурных признаков, учитывающих взаимное расположение пикселей внутри скользящего окна, в [3–5, 7] приводится подход, основанный на использовании матрицы смежности (другое название – матрица распределения градиентов [4]). В дальнейшем будем использовать понятие матрицы смежности
Пусть анализируемое изображение является прямоугольным и имеет x N элементов по горизонтали и y N элементов по вертикали. При этом G ={1,2,..., N} – множество N квантованных значений яркости. Тогда изображение описывается функцией значений яркости из множества G , то есть : x y f L × L →G , где {1,2,..., } x x L = N и {1,2,..., } y y L = N – горизонтальные и вертикальные пространственные области соответственно. Набор x N и y N есть набор
элементов разрешения в растровом изображении. Матрица смежности содержит относительные частоты ij p наличия на изображении соседних элементов, расположенных на расстоянии d друг от друга, с яркостями i, j∈G . Обычно различают горизонтальные (α = 0o ), вертикальные (α = 90o ) и поперечно-диагональные (α = 45o и α = 135o ) пары элементов. Следует отметить, что эти матрицы симметричны, а именно P(i, j,d,α) = P( j,i,d,α) .
На основе вычисленных матриц смежности возможен расчет непосредственно численныхоценок ряда текстурных признаков [5]:


Статистические моменты (9)–(12) позволяют формировать текстурные признаки, учитывающие взаимное расположение соседних пикселей в скользящем окне, и соответственно являются эффективными для описания текстур с выраженной пространственной регулярностью

построение матриц смежности





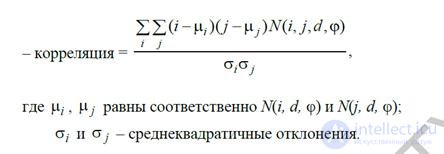
В работе [62] Харалик выделяет другой подход - структурный, или синтаксический. Этот подход развился после возникновения теории формальных языков в середине пятидесятых годов прошлого века. Он основан на том, что текстура составлена из регулярно или почти регулярно повторяющихся непроизводных элементов. Поэтому описание текстуры, как считают сторонники такого подхода, должно состоять из описания непроизводных элементов и правил их размещения [83]. Синтаксическому распознаванию образов посвящена и глава в книге [84]. Выделяют три направления в лингвистическом распознавании:
− Синтаксически ориентированное распознавание, когда устанавливается синтаксис грамматики и разбор грамматики осуществляется в двух направлениях - снизу вверх и сверху вниз.
− Распознавание образов, представленных графами. В рамках разработки этого направления был создан язык описания изображений PDL, предложенный Шоу [85]. Непроизводным элементом в PDL служит любая n-мерная структура с двумя выделенными точками - хвостовой и головной, при этом любая структура рассматривается как ориентированный отрезок прямой, заданный хвостовой и головной точками. Устанавливается допуск на соединение структур примыканием только в головной или хвостовой точках. Таким образом формируются графы структур, а для их обработки используют грамматики цепочек. Этот же подход использован Ледли при анализе хромосом [86].
− Распознавание древовидных структур, при котором модифицируется определение грамматики, дополнительно определяется функция ранжирования. В связи с этим соответственно меняются и правила подстановки.
Стохастические грамматики и языки вводятся для учета случайного характера текстур. Такой подход представлен в работе [87]. Однако авторы
указывают, что их описание чувствительно к шумовым искажениям и не дает хороших результатов при анализе текстур с неявно выраженными
периодическими свойствами, к которым принадлежит большинство реальных изображений.
Эрих и Фойт [88] представляют яркости элементов вдоль строки также в виде дерева соотношений, которое описывает рекурсивное разбиение
функции яркости в точке наименьшего из относительных минимумов. Точки относительных минимумов вновь построенных ветвей дерева и
значения функции яркости слева и справа от минимума используются для дальнейшего разбиения на следующем шаге рекурсии.
Основные проблемы в реализации стохастических грамматик связаны с решением задачи вывода грамматик и получения вероятностей правил
подстановки с помощью обучения, и, до настоящего времени, они имеют ограниченную область применения.
Описание широкого класса процессов и явлений, таких как процессы ограниченной диффузной агрегации, образование вязких пальцев в
пористых средах, турбулентность, процессы диффузии, называемые протеканием, или перколяционными процессами, а также описание
объектов природы, таких как облака, земная поверхность и многие другие,
в терминах фрактальной геометрии определило новое направление в исследованиях - анализ фракталов. При таком подходе авторы не называют
объект текстурой, а называют его фракталом. Поскольку анализ фракталов, по существу, дает характеристику текстуры, и на сегодняшний день нет
устоявшегося определения ни текстуры, ни фрактала, то представляется возможным говорить о фрактальных свойствах текстур. Бенуа Б.
Мандельброт в книге [89], первый назвавший объекты фракталами, изложил как элементарные понятия фрактальной геометрии, так и новые
идеи в этой области, издав общепризнанный стандартный справочник по фракталам. В евклидовой геометрии введено понятие топологической
размерности. Так, размерность кривой - 1, размерность плоскости - 2, поверхности - 3. Таким образом, топологическая размерность имеет
целочисленное значение. Во фрактальной геометрии размерность кривой может иметь значение в интервале [1,2] в зависимости от сложности
кривой, размерность поверхности заключена в интервале [2,3]. Концепция
дробной размерности была впервые сформулирована математиками Хаусдорфом и Безиковичем. Мандельброт назвал такую размерность
фрактальной и ввел такое определение фрактала [89]: “Фракталом называется множество, размерность Хаусдорфа-Безиковича которого строго больше его топологической размерности”.
Распространение фрактального описания объясняется тем, что большинство пространственных систем в природе является нерегулярным и фрагментарным, форма этих систем плохо поддается описанию
аппаратом евклидовой геометрии. Например, береговая линия острова не
прямая и не круглая, и никакая другая классическая кривая не может служить для описания и объяснения ее формы без чрезмерной
искусственности и усложнения.
Определение фрактала претерпевает изменения. В 1987 году в частном
сообщении [63] Мандельброт сузил свое определение: “Фракталом называется структура, состоящая из частей, которые в каком-то
смысле подобны целому”.
Существенным отличительным признаком второго определения является то, что при определении фрактала используется свойство
самоподобия фрактала. Многие кривые и поверхности статистически самоподобны, то есть каждая часть может считаться изображением целогов у меньшенном виде.
Размерность фрактала D определяется как

где 1/r есть отношение подобия, N - число шагов, необходимое для того,
чтобы покрыть кривую.
На рисунке 9.1 проиллюстрировано соотношение между числом шагов и отношением подобия на примере четырех ломаных прямых.
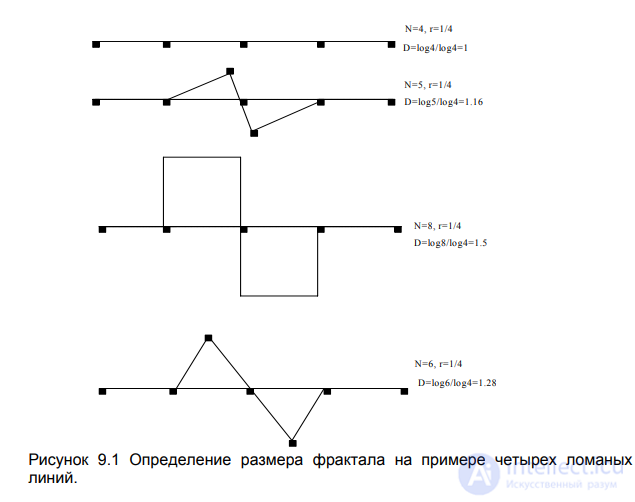
Рисунок 9.1 Определение размера фрактала на примере четырех ломаных линий.
Практически размер фрактала для кривой оценивается путем измерения длин кривой при различных размерах шага. Размерность
фрактала D может быть оценена с помощью следующего уравнения регрессии:
logL=C+BlogG, (9.2)
D=1-B, (9.3)
где L − длина кривой,
B − наклон регрессии,
G − величина шага,
С − константа.
Рассмотрим подробнее реализацию фрактального подхода к анализу облаков. В основу этого метода положено выведенное Мандельбротом соотношение между периметром и площадью объекта [90]. Для
окружностей, квадратов, равносторонних треугольников и других многоугольников отношение периметра к квадратному корню из
ограничиваемой ими площади не зависит от размера фигуры и является
величиной постоянной для данного семейства. Аналогично для семейства
подобных островов отношение длины нефрактальной береговой линии
любого острова к квадратному корню из его площади не зависит от
размера площади. Однако, если береговая линия фрактальна, то ее длина
L(δ) зависит от длины эталона δ и стремится к бесконечности при
стремлении эталона к нулю.
При этом площадь острова ) A(δ , определяемая количеством
располагаемых на ней квадратов 2δ , остается конечной. Таким образом,
отношение периметра к квадратному корню из площади расходится.
Мандельброт получил для случая фрактальной береговой линии
следующее соотношение между периметром и площадью:

Это соотношение выполняется для любого эталона длины δ,
достаточно малого, чтобы удовлетворительно обмерять самый малый из островов.
Соотношение (9.4) применимо при исследовании геометрии облаков и зон дождя, размеры которых заключены в широких пределах от 1 до 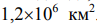 . Выяснилось, что периметр облака связан с его площадью
. Выяснилось, что периметр облака связан с его площадью
соотношением (9.4) с фрактальным размером D = 1,35 ± 0,05 [90]. При этом эти оценки оказались справедливы как для кучевых, так и для
перистых облаков. В работе Ф. Риса и А. Вальдфогеля [91], посвященной анализу фрактальной размерности облаков с мощными конвективными
токами, было установлено соотношение между периметром и площадью для последовательности моментов времени (с интервалом в 1 минуту) в
плоскости сечения для постоянного коэффициента отражения. Основные выводы могут быть следующими: для облаков, периметр которых больше 8 км, размер фрактала примерно совпадает с размером менее мощных облаков и составляет 1,36± 0,1; для облаков периметра от 3 км до 8 км
D=1,0± 0,1 и, наконец, облака с периметром менее 3 км не являются
фракталами.
Исследования фрактальных поверхностей от молекулярных поверхностей белков, обшивки супертанкеров, поверхностей суставов до
взлетных полос аэродромов проводились различными авторами. При этом использовались различные методы оценки размера фрактала, основные из
которых более подробно будут рассмотрены в разделе 9.6.
Таким образом, важной задачей анализа текстур является выделение признаков. Можно отметить три основных подхода к описанию текстур, на
основании которых формируются признаки текстур. Перспективным представляется использование набора признаков, комбинируемых из
признаков, выделяемых при различных подходах к описанию текстур.
При применении методов текстурного анализа мы предполагаем, что входное изображение имеет текстурные характеристики. Поскольку в
настоящее время нет единого определения текстуры, то каждый метод текстурного анализа предполагает описание текстуры некоторым набором
признаков, извлекаемых из изображения. Поэтому при проведении текстурного анализа, прежде всего, необходимо выделить на изображении
текстурные области. В [92] авторы приводят следующую схему оценки текстуры в изображении:
Первые три класса объектов (A,B,C), по мнению авторов, текстурами не являются, к ним в соответствии с рисунком 9.2 относятся: области постоянной яркости, области белого нормального шума и объекты,
полностью описываемые их формой. Белым шумом называется стационарный случайный процесс n(t), у которого спектральная плотность мощности не зависит от частоты и имеет постоянное значение, равное дисперсии значений n(t). Другими словами, все спектральные составляющие белого шума имеют одинаковую мощность. По существу, это идеализированный случайный процесс с бесконечной энергией. Считают, что спектральная плотность мощности шумов слабо изменяется в диапазоне спектра сигнала, который существенно уже спектра шума.
Понятие "белый шум" определяет только равномерный энергетический спектр шума, а законы распределения амплитуды могут быть любыми.
Амплитуда отсчетов белого нормального шума распределена по нормальному закону.
Последние три класса изображений (D,E,F) содержат текстуры и, следовательно, подлежат текстурному анализу. Предварительная грубая
сегментация изображения на текстурные и нетекстурные области производится по методу оценки зернистости текстуры [79]. Зернистость
текстуры оценивается плотностью распределения локальных экстремумов яркости изображения по столбцам и по строкам. Размер фрагмента, в
котором производится оценка зернистости, зависит от ожидаемого диапазона зернистости текстур на изображении.
Чем больше зернистость, тем больший размер фрагмента должен задаваться при анализе. В работе [92] авторы предлагают размер
квадратного фрагмента оценивать по формуле:

где: s - размер стороны фрагмента; min max p , p - минимальная и
максимальная плотности локальных экстремумов изображений, которые
могут быть отнесены к классу текстур, в [92] авторы устанавливают
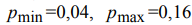 ; n - некоторое, задаваемое пользователем, число
; n - некоторое, задаваемое пользователем, число
локальных экстремумов во фрагменте, например, 32.
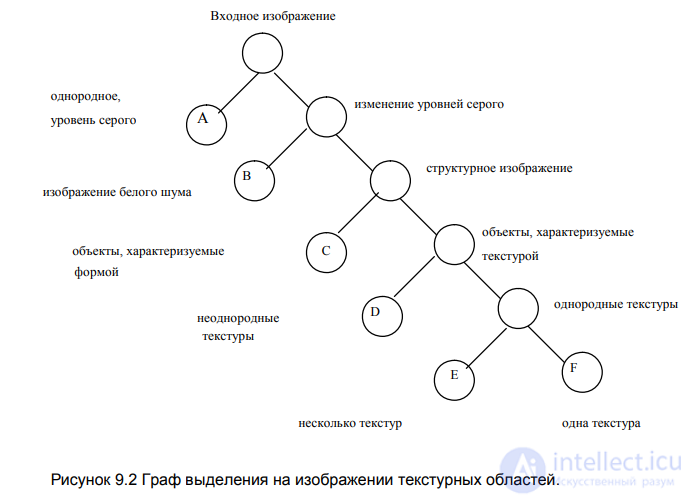
Рисунок 9.2 Граф выделения на изображении текстурных областей.
Поскольку быстродействие этого алгоритма достаточно велико, авторам представляется целесообразным использование его как первогошага при анализе текстур с тем, чтобы выделить те области на изображении, которые подлежат более подробному текстурному анализу.
В заключение, эта статья об текстура подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое текстура, понятие «текстура» статистический подход к обработке текстурных изображений построение матрицы смежности и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Методы и средства компьютерных информационных технологий
Комментарии
Оставить комментарий
Методы и средства компьютерных информационных технологий
Термины: Методы и средства компьютерных информационных технологий