Лекция
Привет, сегодня поговорим про полифазное бпф, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое полифазное бпф, polyphase fft , полифазное быстрое преобразование фурье , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
В цифровой обработке сигналов, без всякого сомнения, основным инструментом анализа является быстрое преобразование Фурье (БПФ). Алгоритм находит применение практически во всех областях науки и техники. Простейшим физическим примером преобразования Фурье может служить восприятие звука человеком. Всякий раз, когда мы слышим звук, ушная раковина автоматически выполняет сложное вычисление, проделать которое человек способен лишь после нескольких лет обучения математике. Суть явления заключается в том, что слуховой орган представляет звук в виде спектра последовательных значений громкости для тонов различной высоты, а мозг превращает получаемую информацию в воспринимаемый звук.
В вопросах радиотехники алгоритмы БПФ находят применение в свертке и при проектировании цифровых корреляторов, используется при обработке изображений, а также в аудио- и видеотехнике (эквалайзеры, спектроанализаторы, вокодеры). Кроме того методы БПФ лежат в основе всевозможных алгоритмов шифрования и сжатия данных (jpeg, mpeg4, mp3), а также при работе с длинными числами. БПФ используется в гидроакустических системах для обнаружения надводных кораблей и подводных лодок, в радиолокационных системах для получения информации о скорости, направлении полета и расстоянии до целей.
Различные модули БПФ имеются в наличии практически в любом пакете прикладных программ, предназначенных для научных исследований, например в Maple, MATLAB, GNU Octave, MathCAD, Mathematica. Специалист должен понимать процесс преобразования Фурье и уметь грамотно его применять для решения поставленных задач, где это необходимо.
Первая программная реализация алгоритма БПФ была осуществлена в начале 60-х годов XX века в вычислительном центре IBM Джоном Кули под руководством Джона Тьюки. В 1965 году ими же была опубликована статья, посвященная алгоритму быстрого преобразования Фурье. Данный метод лег в основу многих алгоритмов БПФ и получил название по фамилиям разработчиков – Cooley-Tukey. С тех пор было выпущено достаточно много различных публикаций и монографий, в которых разрабатываются и описываются различные методы и алгоритмы БПФ, снижающие количество выполняемых операций, уменьшающие энергетические затраты и ресурсы и т.д. На сегодняшний день БПФ – это название не одного, а большого ряда различных алгоритмов, предназначенных для быстрого вычисления преобразования Фурье.
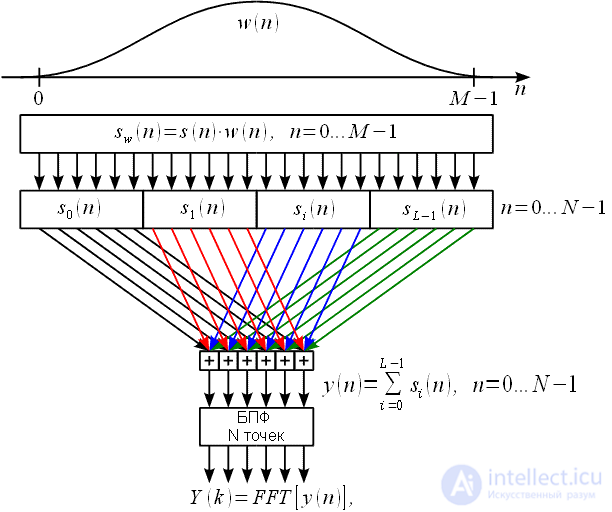
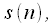
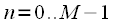 умножается на весовое окно
умножается на весовое окно  , в результате получается сигнал
, в результате получается сигнал 
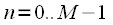 . Этот сигнал делится на
. Этот сигнал делится на 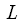 равных частей по
равных частей по 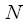 отсчетов, формируются «укороченные» сигналы
отсчетов, формируются «укороченные» сигналы 

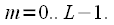 Эти «укороченные» сигналы почленно складываются и формируется один суммарный сигнал
Эти «укороченные» сигналы почленно складываются и формируется один суммарный сигнал (1)
(1)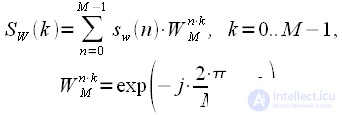 (2)
(2)
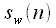 длиной
длиной 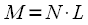 отсчетов:Далее берется
отсчетов:Далее берется 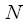 – точечное БПФ от
– точечное БПФ от 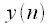 и получается спектр
и получается спектр 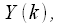
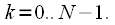
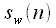 в виде суммы не пересекающихся во времени «укороченных» выборок
в виде суммы не пересекающихся во времени «укороченных» выборок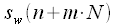 , тогда:
, тогда: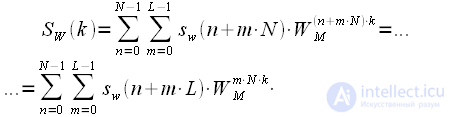 (3)
(3) , тогда
, тогда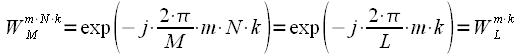 (4)
(4) (5)
(5)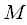 — точечное ДПФ, а нам нужно
— точечное ДПФ, а нам нужно 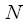 – точечное. Об этом говорит сайт https://intellect.icu . Рассмотрим только
– точечное. Об этом говорит сайт https://intellect.icu . Рассмотрим только 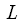 – ые отсчеты спектра
– ые отсчеты спектра 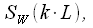
 , тогда (3) c учетом (4) :
, тогда (3) c учетом (4) :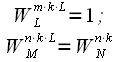 (6)
(6) (7)
(7) (8)
(8)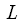 раз спектр исходного взвешенного сигнала. Данное утверждение экспериментально проверено и оно верно. Пример такого прореживания приведен на рисунке 2.
раз спектр исходного взвешенного сигнала. Данное утверждение экспериментально проверено и оно верно. Пример такого прореживания приведен на рисунке 2.

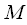 , с хорошим разрешением по частоте поскольку применялось оконное сглаживание, а из него выбираем только
, с хорошим разрешением по частоте поскольку применялось оконное сглаживание, а из него выбираем только 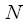 отсчетов путем прореживания по частоте, Для этого требуется только
отсчетов путем прореживания по частоте, Для этого требуется только 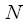 – точечное БПФ.
– точечное БПФ.
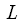 – ый отсчет «перепрыгнем» гармонику и не заметим ее в спектре.
– ый отсчет «перепрыгнем» гармонику и не заметим ее в спектре.

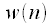 должно быть таким, чтобы обеспечить расширение спектрального пика до
должно быть таким, чтобы обеспечить расширение спектрального пика до 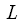 отсчетов. В этом случае мы не сможем его перепрыгнуть выбирая каждый
отсчетов. В этом случае мы не сможем его перепрыгнуть выбирая каждый 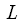 – ый спектральный отсчет. Это наглядно показано на рисунке 4. Рисунок 4a показывает спектр
– ый спектральный отсчет. Это наглядно показано на рисунке 4. Рисунок 4a показывает спектр 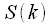 ,
, 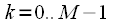 исходного сигнала
исходного сигнала 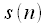 ,
, 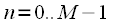 без оконной обработки, рисунок 4б — результат весового сглаживания
без оконной обработки, рисунок 4б — результат весового сглаживания ,
, 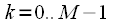 , острые пики стали широкими причем один пик «размазывается» на
, острые пики стали широкими причем один пик «размазывается» на 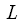 отсчетов, и наконец на рисунке 4в — полифазное БПФ без потери гармоник.
отсчетов, и наконец на рисунке 4в — полифазное БПФ без потери гармоник.

 . Частоту дискретизации возьмем
. Частоту дискретизации возьмем  Гц, количество исходных отсчетов
Гц, количество исходных отсчетов 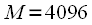 ,
, 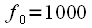 Гц,
Гц, 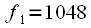 Гц. Выберем
Гц. Выберем 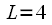 .
.
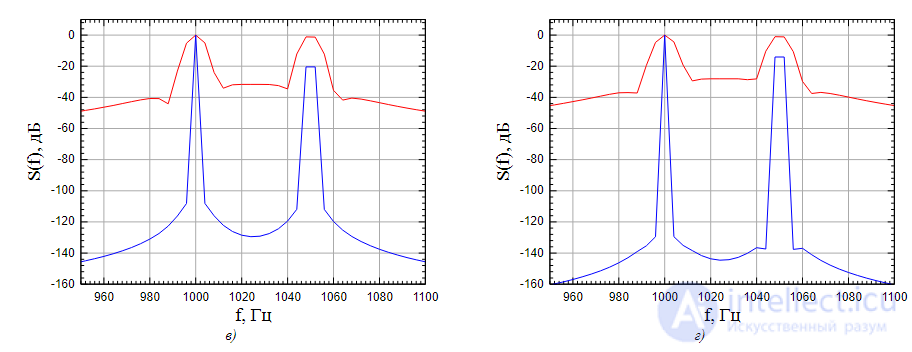
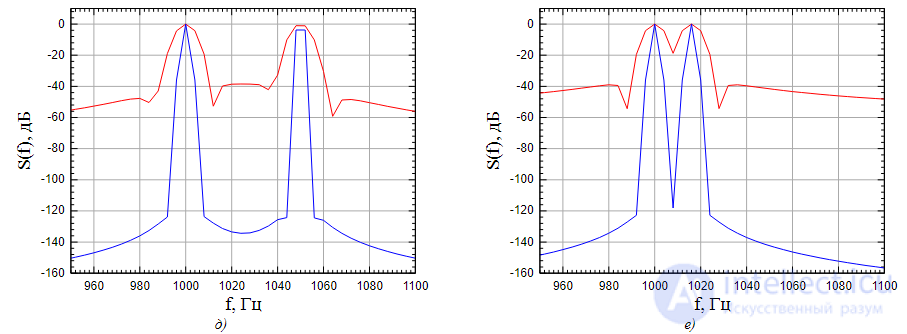
 Гц,
Гц,  Гц. Окно Хемминга как при 1024-точечном БПФ (без полифазной обработки), так и при полифазном БПФ на 4096 точек. Мы попадаем точно на гармоники и видим увеличение разрешения в спектре. Этот пример показывает насколько лучше становится разрешение в спектре при использовании полифазного БПФ. При этом вычислительные затраты примерно одинаковые как на 1024 точечное БПФ без полифазной обработки, так и на полифазное БПФ на 4096 точек (
Гц. Окно Хемминга как при 1024-точечном БПФ (без полифазной обработки), так и при полифазном БПФ на 4096 точек. Мы попадаем точно на гармоники и видим увеличение разрешения в спектре. Этот пример показывает насколько лучше становится разрешение в спектре при использовании полифазного БПФ. При этом вычислительные затраты примерно одинаковые как на 1024 точечное БПФ без полифазной обработки, так и на полифазное БПФ на 4096 точек (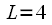 ).
).
 Гц,
Гц,  Гц. Окно Хемминга как при 1024-точечном БПФ (без полифазной обработки), так и при полифазном БПФ на 4096 точек. Пример того как использование полифазного БПФ приводит к потере гармоники из-за неправильно выбранной ширины сглаживающего окна (окно Хемминга слишком узкое).
Гц. Окно Хемминга как при 1024-точечном БПФ (без полифазной обработки), так и при полифазном БПФ на 4096 точек. Пример того как использование полифазного БПФ приводит к потере гармоники из-за неправильно выбранной ширины сглаживающего окна (окно Хемминга слишком узкое).
 Гц,
Гц,  Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и окно Блэкмана при полифазном БПФ на 4096 точек. Видно что окно Блэкмана гораздо лучше подходит для полифазного БПФ, так как потерянная гармоника гораздо выше чем при окне Хемминга, но все равно окно Блэкмана недостаточно широкое, так как уровень гармоники на 20 дБ ниже положенного.
Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и окно Блэкмана при полифазном БПФ на 4096 точек. Видно что окно Блэкмана гораздо лучше подходит для полифазного БПФ, так как потерянная гармоника гораздо выше чем при окне Хемминга, но все равно окно Блэкмана недостаточно широкое, так как уровень гармоники на 20 дБ ниже положенного.
 Гц,
Гц,  Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и окно Блэкмана-Харриса при полифазном БПФ на 4096 точек. Видно что расширение сглаживающего спектрального окна (Блэкмана-Харриса « окно низкого разрешения) увеличивает амплитуду «потерянной» гармоники, но все равно недостаточно.
Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и окно Блэкмана-Харриса при полифазном БПФ на 4096 точек. Видно что расширение сглаживающего спектрального окна (Блэкмана-Харриса « окно низкого разрешения) увеличивает амплитуду «потерянной» гармоники, но все равно недостаточно.
 Гц,
Гц,  Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и максимально-плоское окно при полифазном БПФ на 4096 точек. Уровень потерянной гармоники незначительно ниже реального уровня (примерно на 2...3 дБ). Но наблюдается расширение основного пика при полифазной обработке.
Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и максимально-плоское окно при полифазном БПФ на 4096 точек. Уровень потерянной гармоники незначительно ниже реального уровня (примерно на 2...3 дБ). Но наблюдается расширение основного пика при полифазной обработке.
 Гц,
Гц,  Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и максимально-плоское окно при полифазном БПФ на 4096 точек. Показана возможность различения рядом стоящих сигналов, тогда как при обычном БПФ они сливаются.
Гц. Окно Хемминга при 1024-точечном БПФ (без полифазной обработки), и максимально-плоское окно при полифазном БПФ на 4096 точек. Показана возможность различения рядом стоящих сигналов, тогда как при обычном БПФ они сливаются.
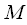 - точечное БПФ
- точечное БПФ 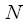 - точечным, или же при тех же вычислительных затратах позволяет обеспечить хорошее разрешение спектрального анализа. Увеличение разрешения анализа обеспечивается полифазной обработкой сигнала на длительном интервале времени. Так как длина исходного сигнала при полифазной обработке в
- точечным, или же при тех же вычислительных затратах позволяет обеспечить хорошее разрешение спектрального анализа. Увеличение разрешения анализа обеспечивается полифазной обработкой сигнала на длительном интервале времени. Так как длина исходного сигнала при полифазной обработке в 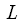 раз длиннее, то и разрешение выше.
раз длиннее, то и разрешение выше.Алгоритмы, связанные с БПФ:
Реализации БПФ:
Другое:
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов