Персептрон принцип работы, виды,Перцептрон Розенблатта

Привет, сегодня поговорим про персептрон, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое персептрон, перцептрон розенблатта , настоятельно рекомендую прочитать все из категории Искусственный интеллект.

Как на самом деле функционируют мозг? Как он строит связи внутри себя? Как происходит процесс обучения нейтронной сети?

Логическая схема перцептрона с тремя выходами

Нейронов случайное число и соединены они случайно. Требуется построить алгоритм соединения, после которого модель будет действовать целесообразно.

персептрон (от слова перцепция - восприятие) можно рассматривать как вариант реализации нейронной сети.

Алгоритм обучения нейронной сети:
di - желаемый выход некоторого i -го эффектора.
yi - текущее состояние эффектора.
E - ошибка между желаемым и действительным. Если она минимальна, то обучение прошло успешно.

Структуру, входные и выходные сигналы менять нельзя. Минимизировать E можно за счет изменения wij.

1 - зависимость скорости изменения ошибки от выходного сигнала персептрона.
2 - зависимость скорости изменения ошибки от входного сигнала персептрона.
3 - зависимость скорости изменения ошибки от веса связи

Алгоритм возвратного вычисления

Мы знаем, что должно быть на выходе и постепенно вычисляем вход от слоя к слою по цепочке формул 1 - 2 - 4 - 2 - 4 - 2 - 4 - : При этом после определения (2) в каждом слое можно вычислить по формуле (3) dw и далее w по формуле: w = w + dw. Реализуется как бы метод градиента.

Задача стоит в следующем: найти все wij, то есть настроить веса всех связей так, чтобы персептрон выдавал нужный выходной сигнал на соответствующий входной. Для настройки (обучения) персептрона на задачу необходимо реализовать множество итераций. Цель уменьшить ошибку Е до нуля. В результате находятся все лучшие значения wij. Обучение происходит экспоненциально. Если ошибка Е не приходит к нулю, то означает, что сложности персептрона мало для обучения данному примеру (примерам), количество слоев или нейронов в слоях надо увеличить.

Общие признаки технологии следующие. Система начинает обнаруживать закономерности во входной информации. Система не знает, как она обучается - ей безразличен предмет рассуждений. Система легко доучивается и переучивается.

На вход подавались 64 изображения. В качестве обучения система должна была выдавать ответ на вопрос - есть ли зеркальная симметрия в картинке. На 64 изображениях она обучалась - ей объясняли есть ли зеркальное изображение или его нет. Затем дали экспертную картинку - изображение, которое до сих пор она не видела. Она точно ответила на задаваемый ей вопрос. Таким образом, эксперимент проходил в две стадии - обучение (персептрону давали ряд примеров) и экспертиза (проверка степени обученности). Каждый персептрон обучался экспоненциально. персептроны обучали решению арифметических примеров, чтению английского текста, распознаванию произносимых букв и т.д.

Персептрон можно "недокормить" примерами, но можно и "перекормить".

Пример: Персептрон 1-го порядка достаточно свободно справляется с задачами распознавания изображений, к которым было применены эффекты масштаба и поворота, но не могут "переварить" сдвиг. Поэтому требуется применить несколько персептронов. Количество персептронов надо увеличивать иерархически, пока сложность системы не сравняется со сложностью задачи.

Описание элементарного перцептрона

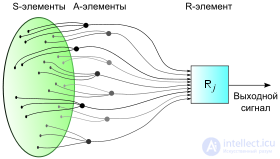
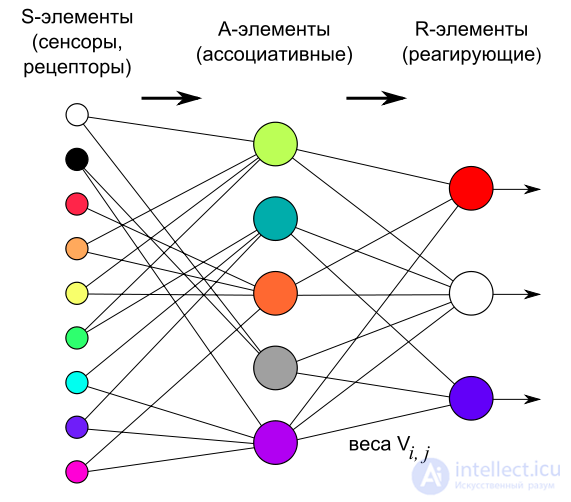
Поступление сигналов с сенсорного поля в решающие блоки элементарного перцептрона в его физическом воплощении.

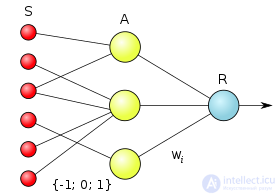
Логическая схема элементарного перцептрона. Веса S—A связей могут иметь значения −1, +1 или 0 (то есть отсутствие связи). Веса A—R связей W могут быть любыми.

Элементарный перцептрон состоит из элементов трех типов: S-элементов, A-элементов и одного R-элемента. S-элементы — это слой сенсоров или рецепторов. В физическом воплощении они соответствуют, например, светочувствительным клеткам сетчатки глаза или фоторезисторам матрицы камеры. Каждый рецептор может находиться в одном из двух состояний — покоя или возбуждения, и только в последнем случае он передает единичный сигнал в следующий слой, ассоциативным элементам.

A-элементы называются ассоциативными, потому что каждому такому элементу, как правило, соответствует целый набор (ассоциация) S-элементов. A-элемент активизируется, как только количество сигналов от S-элементов на его входе превысило некоторую величину θ[nb 5]. Таким образом, если набор соответствующих S-элементов располагается на сенсорном поле в форме буквы «Д», A-элемент активизируется, если достаточное количество рецепторов сообщило о появлении «белого пятна света» в их окрестности, то есть A-элемент будет как бы ассоциирован с наличием/отсутствием буквы «Д» в некоторой области.

Сигналы от возбудившихся A-элементов, в свою очередь, передаются в сумматор R, причем сигнал от i-го ассоциативного элемента передается с коэффициентом [9]. Этот коэффициент называется весом A—R связи.

Так же как и A-элементы, R-элемент подсчитывает сумму значений входных сигналов, помноженных на веса (линейную форму). R-элемент, а вместе с ним и элементарный перцептрон, выдает «1», если линейная форма превышает порог θ, иначе на выходе будет «−1». Математически, функцию, реализуемую R-элементом, можно записать так:

Обучение элементарного перцептрона состоит в изменении весовых коэффициентов {\displaystyle w_{i}} связей A—R. Веса связей S—A (которые могут принимать значения {−1; 0; +1}) и значения порогов A-элементов выбираются случайным образом в самом начале и затем не изменяются. (Описание алгоритма см. ниже.)

После обучения перцептрон готов работать в режиме распознавания[10] или обобщения[11]. В этом режиме перцептрону предъявляются ранее неизвестные ему объекты, и перцептрон должен установить, к какому классу они принадлежат. Работа перцептрона состоит в следующем: при предъявлении объекта возбудившиеся A-элементы передают сигнал R-элементу, равный сумме соответствующих коэффициентов {\displaystyle w_{i}}. Если эта сумма положительна, то принимается решение, что данный объект принадлежит к первому классу, а если она отрицательна — то ко второму[12].

Основные понятия теории перцептронов

Серьезное ознакомление с теорией перцептронов требует знания базовых определений и теорем, совокупность которых и представляет собой основу для всех последующих видов искусственных нейронных сетей. Но, как минимум, необходимо понимание хотя бы с точки зрения теории сигналов, являющееся оригинальным, то есть описанное автором перцептрона Ф. Розенблаттом.

Описание на основе сигналов

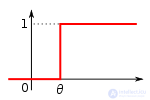
Пороговая функция, реализуемая простыми S- и A-элементами.

Пороговая функция, реализуемая простым R-элементом.

Для начала определим составные элементы перцептрона, которые являются частными случаями искусственного нейрона с пороговой передаточной функцией.

• Простым S-элементом (сенсорным) является чувствительный элемент, который от воздействия какого-либо из видов энергии (например, света, звука, давления, тепла и т. п.) вырабатывает сигнал. Если входной сигнал превышает некоторый порог θ, на выходе элемента получаем +1, в противном случае — 0[13].
• Простым A-элементом (ассоциативным) называется логический решающий элемент, который дает выходной сигнал +1, когда алгебраическая сумма его входных сигналов превышает некоторую пороговую величину θ (говорят, что элемент активный), в противном случае выход равен нулю[13].
• Простым R-элементом (реагирующим, то есть действующим) называется элемент, который выдает сигнал +1, если сумма его входных сигналов является строго положительной, и сигнал −1, если сумма его входных сигналов является строго отрицательной. Если сумма входных сигналов равна нулю, выход считается либо равным нулю, либо неопределенным[13].

Если на выходе любого элемента мы получаем 1, то говорят, что элемент активен или возбужден.

Все рассмотренные элементы называются простыми, так как они реализуют скачкообразные функции. Розенблатт утверждал также, что для решения более сложных задач могут потребоваться другие виды функций, например, линейная[14].

В результате Розенблатт ввел следующие определения:

• Перцептрон представляет собой сеть, состоящую из S-, A-, R-элементов, с переменной матрицей взаимодействия W (элементы которой {\displaystyle w_{ij}} — весовые коэффициенты), определяемой последовательностью прошлых состояний активности сети[14][15].
• Перцептроном с последовательными связями называется система, в которой все связи, начинающиеся от элементов с логическим расстоянием d от ближайшего S-элемента, оканчиваются на элементах с логическим расстоянием d+1 от ближайшего S-элемента[15].
• Простым перцептроном называется любая система, удовлетворяющая следующим пяти условиям:
  1. в системе имеется только один R-элемент (естественно, он связан всеми A-элементами);
  2. система представляет собой перцептрон с последовательными связями, идущими только от S-элементов к A-элементам и от A-элементов к R-элементам;
  3. веса всех связей от S-элементов к A-элементам (S—A связей) неизменны;
  4. время передачи каждой связи равно либо нулю, либо фиксированной постоянной {\displaystyle \tau };
  5. все активирующие функции S-, A-, R-элементов имеют вид {\displaystyle U_{i}(t)=f(a_{i}(t))}, где {\displaystyle a_{i}(t)} — алгебраическая сумма всех сигналов, поступающих одновременно на вход элемента {\displaystyle u_{i}}[14][16]
• Элементарным перцептроном называется простой перцептрон, у которого все элементы — простые. В этом случае его активизирующая функция имеет вид [17].

Дополнительно можно указать на следующие концепции, предложенные в книге, и позднее развитые в рамках теории нейронных сетей:

• Перцептрон с перекрестными связями — это система, в которой существуют связи между элементами одного типа (S, A или R), находящиеся на одинаковом логическом расстоянии от S-элементов, причем все остальные связи — последовательного типа[15].
• Перцептрон с обратной связью — это система, в которой существует хотя бы одна связь от логически более удаленного элемента к менее удаленному[15]. Согласно современной терминологии такие сети называются рекуррентными.
• Перцептрон с переменными S-A связями — это система, в которой снято ограничение на фиксированные связи от S-элементов к A-элементам. Доказано, что путем оптимизации S—A связей можно добиться значительного улучшения характеристик перцептрона[18].

Описание на основе предикатов

Марвин Минский изучал свойства параллельных вычислений, частным случаем которых на то время был перцептрон. Об этом говорит сайт https://intellect.icu . Для анализа его свойств ему пришлось переизложить теорию перцептронов на язык предикатов. Суть подхода заключалась в следующем:[nb 6][19]

• множеству сигналов от S-элементов была сопоставлена переменная X;
• каждому A-элементу был сопоставлен предикат φ(X) (фи от икс), названный частным предикатом;
• каждому R-элементу был сопоставлен предикат ψ (пси), зависящий от частных предикатов;
• наконец, перцептроном было названо устройство, способное вычислять все предикаты типа ψ.

Применительно к «зрительному» перцептрону, переменная X символизировала образ какой-либо геометрической фигуры (стимул). Частный предикат позволял «распознавать» каждый свою фигуру. Предикат ψ означал ситуацию, когда линейная комбинация {\displaystyle a_{1}\phi _{1}+\ldots +a_{n}\phi _{n}} ({\displaystyle a_{i}} — коэффициенты передачи) превышала некоторый порог θ.

Ученые выделили 5 семейств перцептронов, обладающих, по их мнению, интересными свойствами:[20]

1. Перцептроны, ограниченные по диаметру — каждая фигура X, распознаваемая частными предикатами, не превосходит по диаметру некоторую фиксированную величину.
2. Перцептроны ограниченного порядка — каждый частный предикат зависит от ограниченного количества точек из X.
3. Перцептроны Гамбы — каждый частный предикат должен быть линейной пороговой функцией, то есть мини-перцептроном.
4. Случайные перцептроны — перцептроны ограниченного порядка, где частные предикаты представляют собой случайно выбранные булевы функции. В книге отмечается, что именно эта модель наиболее подробно изучалась группой Розенблатта.
5. Ограниченные перцептроны — множество частных предикатов бесконечно, а множество возможных значений коэффициентов {\displaystyle a_{i}} конечно.

Хотя такой математический аппарат позволил применить анализ только к элементарному перцептрону Розенблатта, он вскрыл много принципиальных ограничений для параллельных вычислений, от которых не свободен ни один вид современных искусственных нейронных сетей.

Историческая классификация

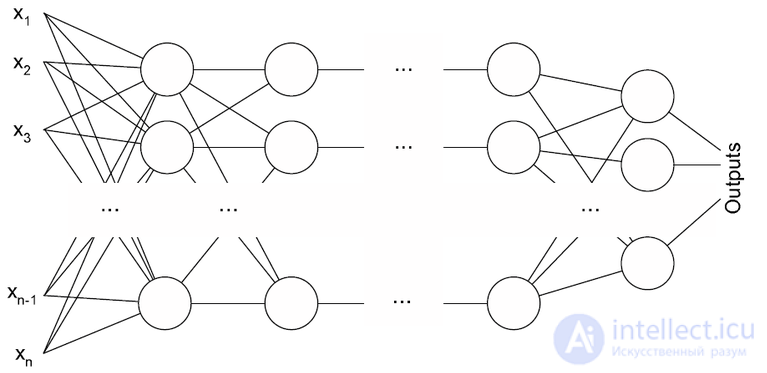
Архитектура многослойного перцептрона (обоих подтипов).

Понятие перцептрона имеет интересную, но незавидную историю. В результате неразвитой терминологии нейронных сетей прошлых лет, резкой критики и непонимания задач исследования перцептронов, а иногда и ложного освещения прессой, изначальный смысл этого понятия исказился. Сравнивая разработки Розенблатта и современные обзоры и статьи, можно выделить 4 довольно обособленных класса перцептронов:

Перцептрон с одним скрытым слоем

Это классический перцептрон, которому посвящена бо́льшая часть книги Розенблатта, и рассматриваемый в данной статье: у него имеется по одному слою S-, A- и R-элементов.

Однослойный перцептрон

Это модель, в которой входные элементы напрямую соединены с выходными с помощью системы весов. Является простейшей сетью прямого распространения — линейным классификатором, и частным случаем классического перцептрона, в котором каждый S-элемент однозначно соответствует одному A-элементу, S—A связи имеют вес +1 и все A-элементы имеют порог θ = 1. Однослойные перцептроны фактически являются формальными нейронами, то есть пороговыми элементами Мак-Каллока — Питтса. Они имеют множество ограничений, в частности, они не могут идентифицировать ситуацию, когда на их входы поданы разные сигналы («задача XOR», см. ниже).

Многослойный перцептрон (по Розенблатту)

Это перцептрон, в котором присутствуют дополнительные слои A-элементов. Его анализ провел Розенблатт в третьей части своей книги.

Многослойный перцептрон (по Румельхарту)

Это перцептрон, в котором присутствуют дополнительные слои A-элементов, причем, обучение такой сети проводится по методу обратного распространения ошибки, и обучаемыми являются все слои перцептрона (в том числе S—A). Является частным случаем многослойного перцептрона Розенблатта.

В настоящее время в литературе под термином «перцептрон» понимается чаще всего однослойный перцептрон (англ. Single-layer perceptron), причем, существует распространенное заблуждение, что именно этот простейший тип моделей предложил Розенблатт. В противоположность однослойному ставят «многослойный перцептрон» (англ. Multilayer perceptron), опять же, чаще всего подразумевая многослойный перцептрон Румельхарта, а не Розенблатта. Классический перцептрон в такой дихотомии относят к многослойным.

Алгоритмы обучения

Важным свойством любой нейронной сети является способность к обучению. Процесс обучения является процедурой настройки весов и порогов с целью уменьшения разности между желаемыми (целевыми) и получаемыми векторами на выходе. В своей книге Розенблатт пытался классифицировать различные алгоритмы обучения перцептрона, называя их системами подкрепления.

Система подкрепления — это любой набор правил, на основании которых можно изменять с течением времени матрицу взаимодействия (или состояние памяти) перцептрона[21].

Описывая эти системы подкрепления и уточняя возможные их виды, Розенблатт основывался на идеях Д. Хебба об обучении, предложенных им в 1949 году[2], которые можно перефразировать в следующее правило, состоящее из двух частей:

• Если два нейрона по обе стороны синапса (соединения) активизируются одновременно (то есть синхронно), то прочность этого соединения возрастает.
• Если два нейрона по обе стороны синапса активизируются асинхронно, то такой синапс ослабляется или вообще отмирает[22].

Обучение с учителем

Классический метод обучения перцептрона — это метод коррекции ошибки[8]. Он представляет собой такой вид обучения с учителем, при котором вес связи не изменяется до тех пор, пока текущая реакция перцептрона остается правильной. При появлении неправильной реакции вес изменяется на единицу, а знак (+/-) определяется противоположным от знака ошибки.

Допустим, мы хотим обучить перцептрон разделять два класса объектов так, чтобы при предъявлении объектов первого класса выход перцептрона был положителен (+1), а при предъявлении объектов второго класса — отрицательным (−1). Для этого выполним следующий алгоритм:[5]

1. Случайным образом выбираем пороги для A-элементов и устанавливаем связи S—A (далее они изменяться не будут).
2. Начальные коэффициенты {\displaystyle w_{i}} полагаем равными нулю.
3. Предъявляем обучающую выборку: объекты (например, круги либо квадраты) с указанием класса, к которым они принадлежат.
   • Показываем перцептрону объект первого класса. При этом некоторые A-элементы возбудятся. Коэффициенты {\displaystyle w_{i}}, соответствующие этим возбужденным элементам, увеличиваем на 1.
   • Предъявляем объект второго класса и коэффициенты {\displaystyle w_{i}} тех A-элементов, которые возбудятся при этом показе, уменьшаем на 1.
4. Обе части шага 3 выполним для всей обучающей выборки. В результате обучения сформируются значения весов связей {\displaystyle w_{i}}.

Теорема сходимости перцептрона[8], описанная и доказанная Ф. Розенблаттом (с участием Блока, Джозефа, Кестена и других исследователей, работавших вместе с ним), показывает, что элементарный перцептрон, обучаемый по такому алгоритму, независимо от начального состояния весовых коэффициентов и последовательности появления стимулов всегда приведет к достижению решения за конечный промежуток времени.

Обучение без учителя

Кроме классического метода обучения перцептрона Розенблатт также ввел понятие об обучении без учителя, предложив следующий способ обучения:

Альфа-система подкрепления — это система подкрепления, при которой веса всех активных связей {\displaystyle c_{ij}}, которые ведут к элементу {\displaystyle u_{j}}, изменяются на одинаковую величину r, а веса неактивных связей за это время не изменяются[23].

Затем, с разработкой понятия многослойного перцептрона, альфа-система была модифицирована и ее стали называть дельта-правило. Модификация была проведена с целью сделать функцию обучения дифференцируемой (например, сигмоидной), что в свою очередь нужно для применения метода градиентного спуска, благодаря которому возможно обучение более одного слоя.

Метод обратного распространения ошибки

Для обучения многослойных сетей рядом ученых, в том числе Д. Румельхартом, был предложен градиентный алгоритм обучения с учителем, проводящий сигнал ошибки, вычисленный выходами перцептрона, к его входам, слой за слоем. Сейчас это самый популярный метод обучения многослойных перцептронов. Его преимущество в том, что он может обучить все слои нейронной сети, и его легко просчитать локально. Однако этот метод является очень долгим, к тому же, для его применения нужно, чтобы передаточная функция нейронов была дифференцируемой. При этом в перцептронах пришлось отказаться от бинарного сигнала, и пользоваться на входе непрерывными значениями[24].

Традиционные заблуждения

В результате популяризации искусственных нейронных сетей журналистами и маркетологами был допущен ряд неточностей, которые, при недостаточном изучении оригинальных работ по этой тематике, неверно истолковывались молодыми (на то время) учеными. В результате по сей день можно встретиться с недостаточно глубокой трактовкой функциональных возможностей перцептрона по сравнению с другими нейронными сетями, разработанными в последующие годы.[когда?]

Терминологические неточности

Самая распространенная ошибка, связанная с терминологией, это определение перцептрона как нейронной сети без скрытых слоев (однослойного перцептрона, см. выше). Эта ошибка связана с недостаточно проработанной терминологией в области нейросетей на раннем этапе их разработки. Ф. Уоссерменом была сделана попытка определенным образом классифицировать различные виды нейронных сетей:

Как видно из публикаций, нет общепринятого способа подсчета числа слоев в сети. Многослойная сеть состоит из чередующихся множеств нейронов и весов. Входной слой не выполняет суммирования. Эти нейроны служат лишь в качестве разветвлений для первого множества весов и не влияют на вычислительные возможности сети. По этой причине первый слой не принимается во внимание при подсчете слоев, и сеть считается двухслойной, так как только два слоя выполняют вычисления. Далее, веса слоя считаются связанными со следующими за ними нейронами. Следовательно, слой состоит из множества весов со следующими за ними нейронами, суммирующими взвешенные сигналы[25].

В результате такого представления перцептрон попал под определение «однослойная нейронная сеть». Отчасти это верно, потому что у него нет скрытых слоев обучающихся нейронов (веса которых адаптируются к задаче). И поэтому всю совокупность фиксированных связей системы из S- к A-элементам, можно логически заменить набором (модифицированных по жесткому правилу) новых входных сигналов, поступающих сразу на А-элементы (устранив тем самым вообще первый слой связей). Но тут как раз не учитывают, что такая модификация превращает нелинейное представление задачи в линейное.

Поэтому просто игнорирование не обучаемых слоев с фиксированными связями (в элементарном перцептроне это S—A связи) позволяет делать неправильные выводы о возможностях нейросети. Так, Минский поступил очень корректно, переформулировав А-элемент как предикат (то есть функцию); наоборот, Уоссермен уже потерял такое представление и у него А-элемент — просто вход (почти эквивалентный S-элементу). При такой терминологической путанице упускается из виду тот факт, что в перцептроне происходит отображение рецептивного поля S-элементов на ассоциативное поле А-элементов, в результате чего и происходит преобразование любой линейно неразделимой задачи в линейно разделимую.

Функциональные заблуждения

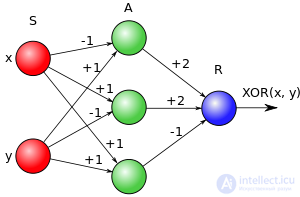
Решение элементарным перцептроном «задачи XOR». Порог всех элементов θ = 0.

Большинство функциональных заблуждений сводятся к якобы невозможности решения перцептроном линейно неразделимой задачи. Но вариаций на эту тему достаточно много, рассмотрим главные из них.

Задача XOR

Заблуждение: перцептрон не способен решить «задачу XOR».

Очень распространенное и самое несерьезное заявление. На изображении справа показано решение этой задачи перцептроном. Данное заблуждение возникает, во-первых, из-за того, что неправильно интерпретируют определение перцептрона, данного Минским (см. выше), а именно, предикаты сразу приравнивают входам, хотя предикат у Минского — это функция, идентифицирующая целый набор входных значений[nb 7]. Во-вторых, из-за того, что классический перцептрон розенблатта путают с однослойным перцептроном (из-за терминологической неточности, описанной выше).

Следует обратить особое внимание на то, что «однослойный перцептрон» в современной терминологии и «однослойный перцептрон» в терминологии Уоссермана — разные объекты. И объект, изображенный на иллюстрации, в терминологии Уоссермана есть двухслойный перцептрон.

Обучаемость линейно неразделимым задачам

Заблуждение: выбором случайных весов можно достигнуть обучения и линейно неразделимым (вообще, любым) задачам, но только если повезет, и в новых переменных (выходах A-нейронов) задача окажется линейно разделимой. Но может и не повезти.

Теорема сходимости перцептрона[8] доказывает, что нет и не может быть никакого «может и не повезти»; при равенстве А-элементов числу стимулов и не особенной G-матрице — вероятность решения равна 100 %. То есть при отображении рецепторного поля на ассоциативное поле большей на одну размерности случайным (нелинейным) оператором нелинейная задача превращается в линейно разделимую. А следующий обучаемый слой уже находит линейное решение в другом пространстве входов.

Например, обучение перцептрона для решения «задачи XOR» (см. на иллюстрации) проводится следующими этапами:

Веса	Итерации
	1			2	3		4		5
w1	0	1	1	1	1	2	2	2	2
w2	0	0	1	1	1	1	1	2	2
w3	−1	0	1	0	−1	0	−1	0	−1
Входные сигналы (x, y)	1, 1	0, 1	1, 0	1, 1	1, 1	0, 1	1, 1	1, 0	1, 1

Обучаемость на малом числе примеров

Заблуждение: если в задаче размерность входов довольно высока, а обучающих примеров мало, то в таком «слабо заполненном» пространстве число удач может и не оказаться малым. Это свидетельствует лишь о частном случае пригодности перцептрона, а не его универсальности.

Данный аргумент легко проверить на тестовой задаче под названием «шахматная доска» или «губка с водой»[26][nb 8]:

Дана цепочка из 2·N единиц или нулей, параллельно поступающих на входы перцептрона. Если эта цепочка является зеркально симметричной относительно центра, то на выходе +1, иначе 0. Обучающие примеры — все (это важно) {\displaystyle 2^{2N}} цепочек.

Могут быть вариации данной задачи, например:

Возьмем черно-белое изображение размером 256×256 элементов (пикселей). Входными данными для перцептрона будут координаты точки (8 бит + 8 бит, итого нужно 16 S-элементов), на выходе потребуем цвет точки. Обучаем перцептрон всем точкам (всему изображению). В итоге имеем 65 536 различных пар «стимул—реакция». Обучить без ошибок.

Если данный аргумент справедлив, то перцептрон не сможет ни при каких условиях обучиться, не делая ни одной ошибки. Иначе перцептрон не ошибется ни разу.

На практике оказывается, что данная задача очень проста для перцептрона: чтобы ее решить, перцептрону достаточно 1500 А-элементов (вместо полных 65 536, необходимых для любой задачи). При этом число итераций порядка 1000. При 1000 А-элементов перцептрон не сходится за 10 000 итераций. Если же увеличить число А-элементов до 40 000, то схождения можно ожидать за 30—80 итераций.

Такой аргумент появляется из-за того, что данную задачу путают с задачей Минского «о предикате „четность“»[27].

Стабилизация весов и сходимость

Заблуждение: в перцептроне Розенблатта столько А-элементов, сколько входов. И сходимость по Розенблатту, это стабилизация весов.

У Розенблатта читаем:

Если число стимулов в пространстве W равно n > N (то есть больше числа А-элементов элементарного перцептрона), то существует некоторая классификация С(W), для которой решения не существует[28].

Отсюда следует, что:

1. у Розенблатта число А-элементов равно числу стимулов (обучающих примеров), а не числу входов;
2. сходимость по Розенблатту, это не стабилизация весов, а наличие всех требуемых классификаций, то есть по сути отсутствие ошибок.

Экспоненциальный рост числа скрытых элементов

Заблуждение: если весовые коэффициенты к элементам скрытого слоя (А-элементам) фиксированы, то необходимо, чтобы количество элементов скрытого слоя (либо их сложность) экспоненциально возрастало с ростом размерности задачи (числа рецепторов). Тем самым, теряется их основное преимущество — способность решать задачи произвольной сложности при помощи простых элементов.

Розенблаттом было показано, что число А-элементов зависит только от числа стимулов, которые нужно распознать (см. предыдущий пункт или теорему сходимости перцептрона). Таким образом, при возрастании числа рецепторов, если количество А-элементов фиксировано, непосредственно не зависит возможность перцептрона к решению задач произвольной сложности.

Такое заблуждение происходит от следующей фразы Минского:

При исследовании предиката «четность» мы видели, что коэффициенты могут расти с ростом |R| (числа точек на изображении) экспоненциально[29].

Кроме того, Минский исследовал и другие предикаты, например «равенство». Но все эти предикаты представляют собой достаточно специфическую задачу на обобщение, а не на распознавание или прогнозирование. Так, например, чтобы перцептрон мог выполнять предикат «четность» — он должен сказать, четно или нет число черных точек на черно-белом изображении; а для выполнения предиката «равенство» — сказать, равна ли правая часть изображения левой. Ясно, что такие задачи выходят за рамки задач распознавания и прогнозирования, и представляют собой задачи на обобщение или просто на подсчет определенных характеристик. Это и было убедительно показано Минским, и является ограничением не только перцептронов, но и всех параллельных алгоритмов, которые не способны быстрее последовательных алгоритмов вычислить такие предикаты.

Поэтому такие задачи ограничивают возможности всех нейронных сетей и перцептронов в частности, но это никак не связанно с фиксированными связями первого слоя; так как во-первых, речь шла о величине коэффициентов связей второго слоя, а во-вторых, вопрос только в эффективности, а не принципиальной возможности. То есть перцептрон можно обучить и этой задаче, но требуемые для этого емкость памяти и скорость обучения будут больше, чем при применении простого последовательного алгоритма. Введение же обучаемых весовых коэффициентов в первом слое лишь ухудшит положение дел, ибо потребует большего времени обучения, потому что переменные связи между S и A скорее препятствуют, чем способствуют процессу обучения[30]. Причем, при подготовке перцептрона к задаче распознавания стимулов особого типа, для сохранения эффективности потребуются особые условия стохастического обучения[31], что было показано Розенблаттом в экспериментах с перцептроном с переменными S—A связями.

Возможности и ограничения модели

Возможности модели

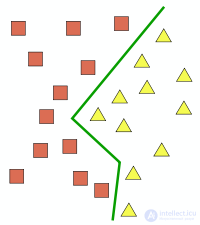
Пример классификации объектов. Зеленая линия — граница классов.

Сам Розенблатт рассматривал перцептрон прежде всего как следующий важный шаг в сторону исследования и использования нейронных сетей, а не как оконченный вариант «машины, способной мыслить»[nb 9]. Еще в предисловии к своей книге он, отвечая на критику, отмечал, что «программа по исследованию перцептрона связана главным образом не с изобретением устройств, обладающих „искусственным интеллектом“, а с изучением физических структур и нейродинамических принципов»[32].

Розенблатт предложил ряд психологических тестов для определения возможностей нейросетей: эксперименты по различению, обобщению, по распознаванию последовательностей, образованию абстрактных понятий, формированию и свойствам «самосознания», творческого воображения и другие[33]. Некоторые из этих экспериментов далеки от современных возможностей перцептронов, поэтому их развитие происходит больше философски в пределах направления коннективизма. Тем не менее, для перцептронов установлены два важных факта, находящие применение в практических задачах: возможность классификации (объектов) и возможность аппроксимации (границ классов и функций)[34].

Важным свойством перцептронов является их способность к обучению, причем по довольно простому и эффективному алгоритму (см. выше).

Ограничения модели

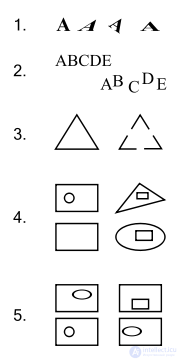
Некоторые задачи, которые перцептрон не способен решить: 1, 2 — преобразования группы переносов; 3 — из какого количества частей состоит фигура? 4 — внутри какого объекта нет другой фигуры? 5 — какая фигура внутри объектов повторяется два раза? (3, 4, 5 — задачи на определение «связности» фигур.)

Сам Розенблатт выделил два фундаментальных ограничения для трехслойных перцептронов (состоящих из одного S-слоя, одного A-слоя и R-слоя): отсутствие у них способности к обобщению своих характеристик на новые стимулы или новые ситуации, а также неспособность анализировать сложные ситуации во внешней среде путем расчленения их на более простые[17].

В 1969 году Марвин Минский и Сеймур Паперт опубликовали книгу «Перцептроны», где математически показали, что перцептроны, подобные розенблаттовским, принципиально не в состоянии выполнять многие из тех функций, которые хотели получить от перцептронов. К тому же, в то время была слабо развита теория о параллельных вычислениях, а перцептрон полностью соответствовал принципам таких вычислений. По большому счету, Минский показал преимущество последовательных вычислений перед параллельным в определенных классах задач, связанных с инвариантным представлением. Его критику можно разделить на три темы:

1. Перцептроны имеют ограничения в задачах, связанных с инвариантным представлением образов, то есть независимым от их положения на сенсорном поле и относительно других фигур. Такие задачи возникают, например, если нам требуется построить машину для чтения печатных букв или цифр так, чтобы эта машина могла распознавать их независимо от положения на странице (то есть чтобы на решение машины не оказывали влияния перенос, поворот, растяжение-сжатие символов)[6]; или если нам нужно определить из скольких частей состоит фигура[35]; или находятся ли две фигуры рядом или нет[36]. Минским было доказано, что этот тип задач невозможно полноценно решить с помощью параллельных вычислений, в том числе — перцептрона.
2. Перцептроны не имеют функционального преимущества над аналитическими методами (например, статистическими) в задачах, связанных с прогнозированием[37]. Тем не менее, в некоторых случаях они представляют более простой и производительный метод анализа данных.
3. Было показано, что некоторые задачи в принципе могут быть решены перцептроном, но могут потребовать нереально большого времени[38] или нереально большой памяти[39].

Книга Минского и Паперта существенно повлияла на пути развития науки об искусственном интеллекте, так как переместила научный интерес и субсидии правительственных организаций США на другое направление исследований — символьный подход в ИИ.

Применение перцептронов

Здесь будут показаны только основы практического применения перцептрона на двух различных задачах. Задача прогнозирования (и эквивалентная ей задача распознавания образов) требует высокой точности, а задача управления агентами — высокой скорости обучения. Поэтому, рассматривая эти задачи, можно полноценно ознакомиться с возможностями перцептрона, однако этим далеко не исчерпываются варианты его использования.

В практических задачах от перцептрона потребуется возможность выбора более чем из двух вариантов, а значит, на выходе у него должно находиться более одного R-элемента. Как показано Розенблаттом, характеристики таких систем не отличаются существенно от характеристик элементарного перцептрона[40].

Прогнозирование и распознавание образов

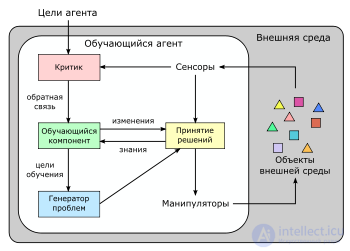
Взаимодействие обучающегося агента со средой. Важной частью такой системы являются обратные связи.

В этих задачах от перцептрона требуется установить принадлежность объекта к какому-либо классу по его параметрам (например, по внешнему виду, форме, силуэту). Причем, точность распознавания будет во многом зависеть от представления выходных реакций перцептрона. Здесь возможны три типа кодирования: конфигурационное, позиционное, и гибридное. Позиционное кодирование, когда каждому классу соответствует свой R-элемент, дает более точные результаты, чем другие виды. Такой тип использован, например, в работе Э. Куссуль и др. «Перцептроны Розенблатта для распознавания рукописных цифр». Однако оно неприменимо в тех случаях, когда число классов значительно, например, несколько сотен. В таких случаях можно применять гибридное конфигурационно-позиционное кодирование, как это было сделано в работе С. Яковлева «Система распознавания движущихся объектов на базе искусственных нейронных сетей».

Управление агентами

В искусственном интеллекте часто рассматриваются обучающиеся (адаптирующиеся к окружающей среде) агенты. При этом в условиях неопределенности становится важным анализировать не только текущую информацию, но и общий контекст ситуации, в которую попал агент, поэтому здесь применяются перцептроны с обратной связью[41]. Кроме того, в некоторых задачах становится важным повышение скорости обучения перцептрона, например, с помощью моделирования рефрактерности[42].

После периода, известного как «Зима искусственного интеллекта», интерес к кибернетическим моделям возродился в 1980-х годах, так как сторонники символьного подхода в ИИ так и не смогли подобраться к решению вопросов о «Понимании» и «Значении», из-за чего машинный перевод и техническое распознавание образов до сих пор обладает неустранимыми недостатками. Сам Минский публично выразил сожаление, что его выступление нанесло урон концепции перцептронов, хотя книга лишь показывала недостатки отдельно взятого устройства и некоторых его вариаций. Но в основном ИИ стал синонимом символьного подхода, который выражался в составлении все более сложных программ для компьютеров, моделирующих сложную деятельность человеческого мозга.

Вау!! 😲 Ты еще не читал? Это зря!

• Сверточная нейронная сеть
• Байесовская сеть
• Когнитрон
• История искусственного интеллекта
• Стереотип

Надеюсь, эта статья об увлекательном мире персептрон, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое персептрон, перцептрон розенблатта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Искусственный интеллект