Механизмы обучения. Естественные объекты. Автомат с линейной тактикой. Доверчивый (автомат Кринского). Осторожный Крылова. Коллектив автоматов

Лекция

Привет, сегодня поговорим про естественные объекты, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое естественные объекты, автомат с линейной тактикой, доверчивый автомат, автомат кринского, осторожный автомат крылова, коллектив автоматов , настоятельно рекомендую прочитать все из категории Искусственный интеллект.

Цель - построить техническую систему, реализующую механизм обучения и самообучения. Система должна реализовать не худшую способность к обучению, чем живое существо. Для этого требуется исследовать, как обучаются живые существа.

естественные объекты

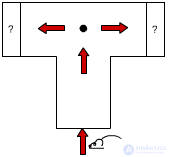
рис.3.1 T - образный лабиринт

Рассмотрим T - образный лабиринт (рисунок 3.1). В него заводится зверюшка. Заранее она не знает, что ожидает в каждой из сторон лабиринта, пища или удар электрического тока (поощрение или наказание). Опыт повторяется многократно. Сначала справа всегда была пища, а слева ток. Зверюшка бежала случайно только первые несколько раз, затем она обучалась и шла к пище. Опыт усложнили: теперь еда и наказание были в обеих частях лабиринта, но выбирались они с определенной постоянной вероятностью. Справа Р = 0.4, слева - 0.9, где Р - вероятность штрафа. Вместо детерминированной среды зверюшка попадала в вероятностную детерминированную среду. В результате опыта зверюшка шла направо - она улавливала как рационально поступать в новых условиях. Затем ее поместили вероятностную недетерминированную среду, т.е. в вероятность штрафа стала изменяться во времени.
P(t). Зверюшка переучивалась и здесь.

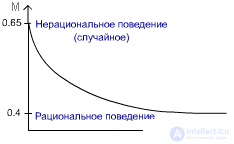
Механизмы обучения. Естественные объекты. Автомат с линейной тактикой. Доверчивый (автомат Кринского). Осторожный Крылова. Коллектив автоматов

рис.3.2

Для нерационального поведения характерно то, что выбор направления осуществляется случайно. С равными вероятностями зверюшка может убежать и направо, и налево: M = 0.5*0.9 + 0.5*0.4 = 0.65 Для рационального поведения: M = 0*0.9 + 1*0.4 = 0.4 Способность к обучению можно измерять рациональностью поведения. E = (P_л,P_п), где E -среда, Pл,Pп - вероятности наказания средой при действиях d1,d2 соответственно. В нашем случае d1 - пойти налево, d2 - пойти направо. Среда двухкомпонентная, т.к. возможны только два действия.

Задача: спроектировать техническое устройство, с целесообразным поведением в заранее неизвестной среде.

автомат с линейной тактикой

рис.3.3

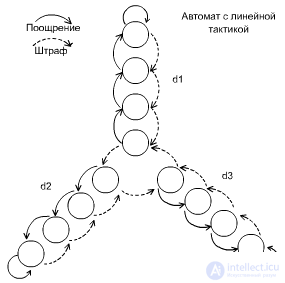
Автомат с линейной тактикой был предложен в свое время и изучен М.Л. Цетлиным , который рассмотрел его поведение в вероятностной среде, наказывающей или поощряющей автомат за совершенное действие с некоторыми фиксированными вероятностями.

Первой конструкцией был автомат с линейной тактикой — автомат с двумя состояниями, который в одном состоянии выдает на выходе сигнал о том, что он совершает действие d1, в другом — о том, что он совершает действие d2. За ошибочное действие автомат штрафуется и переводится в другое состояние, а за верное поощряется и сохраняет свое состояние, после чего действие повторяется.

Обучающийся автомат должен минимизировать суммарный штраф за все время своей жизни. Простейший автомат превращается в автомат с линейной тактикой после того, как увеличивается количество состояний, в которых он выполняет одинаковое действие. С современных позиций работы Цетлина можно отнести к обучению с подкреплением (reinforcement learning), когда модель обучается по обратной связи при взаимодействии с внешней средой.

Автомат реализует три действия d1,d2, d3. Трехкомпонентная среда. Пусть среда ведет себя следующим образом: E = (0.9, 0.0001, 0.8). Если среда штрафует, то мы всплываем (из глубины лепестка), если поощряет, то уходим в глубь лепестка. Пусть первоначальным состоянием автомата было одно из состоянии в лепестке d1. Т.к. вероятность штрафа здесь довольно велика (0.9), то спустя некоторое время автомат перейдет в состояние, находящееся в d3, и будет оставаться там продолжительное время. То есть автомат ведет себя наилучшим образом в заранее неизвестной среде.

Автомат описывается парой чисел. Первое - количество действий автомата, и второе - глубина лепестка (q). Приведенный автомат описывается как (3,4). Об этом говорит сайт https://intellect.icu . q - базовый параметр, аналог инертности. Чем q больше, тем целесообразнее ведет себя автомат. У человека q находится в пределах от 3 до 5. Чем q больше, тем хуже объект приспосабливается к часто меняющейся среде. Для нестационарной среды лучше аппараты с меньшим q, для стационарной с большим q.

Доверчивый автомат ( автомат кринского )

рис.3.4 Введен нюанс темперамента. Действует так же, как предыдущий.

Автомат с линейной тактикой аккуратен и педантичен. Неторопливо движется он по состояниям лепестков, отсчитывая число поступивших на его вход наказаний и поощрений. Но возможны и другие автоматы. Вот один из них, предложенный В. И. Кринским. Он похож на автомат с линейной тактикой и действует при поступлении сигнала штраф аналогично автомату с линейной тактикой. Но при сигнале поощрение его поведение резко отлично от педантизма автомата с линейной тактикой. В каком бысостоянии лепестка в этот момент не был автомат В. И. Кринского, он тут же меняет его на самое глубокое для данного лепестка состояние. Соответствующая картина показана на рис. 2.4 (пока не следует обращать внимание на штрихпунктирные линии). Такой автомат можно назвать «доверчивым». Он всегда «верит» в хорошее. И всякий положительный сигнал от среды приводит его в состояние «эйфории». Казалось бы, подобный способ поведения ничего кроме неприятностей автомату не сулит. Но мир автоматов оригинален и странен. Строго доказано, что доверчивые автоматы В. И. Кринского ведут себя целесообразно в любых стационарных случайных средах, а последовательность подобных автоматов с ростом их глубины памяти q образует асимптотически оптимальную последовательность.

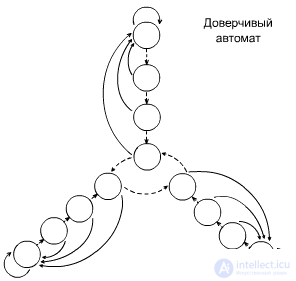
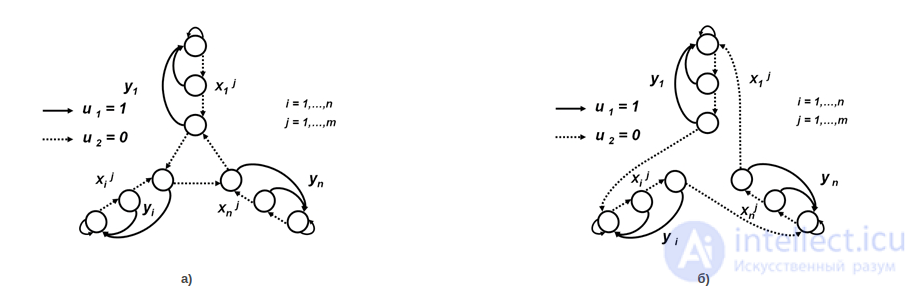
Механизмы обучения. Естественные объекты. Автомат с линейной тактикой. Доверчивый (автомат Кринского). Осторожный Крылова. Коллектив автоматов

Доверчивый автомат Кринского по принципам своего построения и функционирования во многом аналогичен автомату Цетлина. Как показано на рис. 7 а), основное отличие заключается в переходе текущего состояния автомата на максимально глубокий уровень хранения при получении положительного отклика на выполненное действие.

Рис. 7. Диаграммы переходов доверчивого автомата Кринского (а)) и автомата Роббинса (б))

При поступлении сигнала штраф, поведение этого автомата аналогично поведению автомата с линейной тактикой Цетлина, но при получении сигнала поощрения, этот автомат, независимо в каком состоянии лепестка он находился в данный момент, переходит в самое глубокое состояние данного лепестка. Этот автомат, как будто, склонен верить в хорошее, и положительный сигнал среды приводит его в состояние «эйфории».

Строго доказано, что автоматы Кринского ведут себя целесообразно в любых стационарных случайных средах.

Может сложиться ощущение, что любые меры по увеличению числа инерционности автомата, улучшает показатель целесообразности поведения автомата.

Ситуация качественно меняется, если наш линейный автомат имеет дело с динамической средой. Если смена сред происходит достаточно быстро, то инерционность вряд ли может служить хорошим средством для существования в этом мире. Ведь в динамическом мире надо быстро следить за возникающими изменениями среды, и для любого динамического мира необходима своя глубина памяти, выбранная в зависимости от скорости изменения обстановки.

осторожный автомат крылова

Автомат с линейной тактикой, но при поощрениях доверяет не сразу, а с вероятностью 0.5 определяет верить или нет поощрению.

Можно построить нецелесообразный автомат. Например, "Иван-дурак" - автомат с двумя действиями (плакать и смеяться) и глубиной - 1.

рис.3.5

Опишем еще одну конструкцию автомата, обеспечивающего целесообразное поведение в любой стационарной среде и дающего возможность построить асимптотически оптимальную последовательность автоматов, позволяющую получать минимальный возможный штраф в данной среде с любой наперед заданной точностью. В отличие от ранее рассмотренных конструкций этот автомат будет не детерминированным, а вероятностным. Устроен он подобно автомату с линейной тактикой. При поступлении сигнала нештраф смена состояний в нем происходит так, как показано на рис. 2.3. Но при сигнале штраф такой автомат не спешит менять состояние. Сначала он «подбрасывает монетку» и по результату подбрасывания либо переходит в состояние по пунктирной стрелке, показанной на рис. 2.3, либо сохраняет то состояние, в котором автомат получил сигнал штраф. Эта конструкция, предложенная В. Ю. Крыловым, может быть названа «осторожным» автоматом.

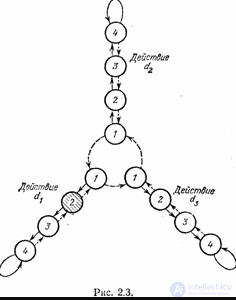
рис 2.3

Какая глубина лучше?

На рисунке 3.6 показан график зависимости целесообразности от глубины с учетом частоты изменения среды. Лучше всего настраивать величину q в зависимости от среды.

рис.3.6

Коллектив автоматов

рис.3.7

Коллектив автоматов - это усиленная независимая система взаимодействующих автоматов, применяемая, например, для решения задачи обхода. В отличие от независимых систем автоматов коллектив автоматов анализирует лабиринты с учетом положения его «членов» в лабиринте. Коллективы автоматов могут быть снабжены камнями, играющими роль ограниченной внешней памяти для коллективов. Камень — это флажок-метка, который может быть или «на руках» у любого автомата, или в некоторой вершине обследуемого коллективом лабиринта. Автомат может забирать или оставлять камень в вершине, в которой оказался, но общее количество камней у данного коллектива всегда является постоянным. Камни можно рассматривать также как автоматы простейшего вида, перемещение которых полностью определяется другими автоматами коллектива. Ф. Хофман [33, 34] установил, что коллектив из одного автомата и одного камня не может обойти все конечные плоские мозаичные лабиринты; М. Блюм и Д. Козен показали, что коллектив из одного автомата и двух камней решает эту задачу, отметив при этом, что коллектив из двух автоматов также решает эту задачу. Наряду с этим в работах А. Хемерлинга [27] и К. Кригела [43] показано, что класс указанных лабиринтов допускает естественное расслоение, такое, что для любого его слоя найдется коллектив из одного автомата с камнем, обходящий этот слой; в качестве параметра расслоения здесь выступает число дыр в лабиринте.

Теорема 1 Не существует коллектив автоматов, обходящий все 3-мерные инициальные конечные мозаичные лабиринты. Доказательство этой теоремы проводится посредством построения ловушки для заданного коллектива автоматов. Это утверждение было впервые сформулировано и частично обосновано в . Его доказательство дается в работе [30], где показано, что для любого конечного множества коллективов автоматов существует конечная 3-мерная мозаичная инициальная ловушка ограниченной «толщины» — все ее вершины лежат только в двух плоскостях

Дано поле ресурсов. В каждой клетке - автомат с линейной тактикой (4,4). Для определенности оставим 10 автоматов. Автомат может реализовывать следующие действия: остаться на месте, пойти вправо, пойти влево, пойти вверх (вниз).
1) Если автоматы останутся, как были, то вместе получат 1*100 + 9*40 = 460 единиц. Цена игры:
460/10 = 46 ед. Но т.к. один получает 100, а другие по 40, то это заставит автоматы перебегать с одного места в другое. Состояние неустойчивое.
2) Другая, более устойчивая конфигурация, когда два автомата сидят на "хлебной" клетке. Все вместе получат: 2*50 + 8*40 = 420; цена игры 420/10 = 42 ед;

С точки зрения общественной выгоды - лучше первая ситуация, т.к. в среднем "на душу населения" получен более высокий результат. Но с точки зрения индивидуальной выгоды - лучше вторая ситуация. Первая получила название игры Мора, вторая - игры Нэша. Устойчивый коллектив тот, где каждый руководствуется собственной выгодой.

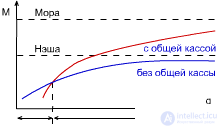
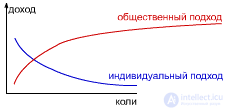
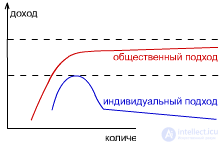
Но можно ли сыграть в устойчивую игру Мора? Т.е. получить максимальную общественную выгоду, при этом сохраняя устойчивое состояние. Для этого требуется сыграть в игру с общей кассой: все играют в игру Мора, но затем все делится поровну.

Если автоматы имеют большой q, то им выгоднее играть в игру Мора, т.к. они более инерционные; и наоборот - если q низкий, то в игру Нэша, т.к. они более активные.

рис.3.8

Но все ли среды имеют подобные свойства? Есть среды, которые не подчиняются вышеприведенным выводам.

рис.3.9

рис.3.10

На рисунке 3.9 - сбор грибов. На рисунке 3.10 - охота на лося.

Вау!! 😲 Ты еще не читал? Это зря!

Надеюсь, эта статья об увлекательном мире естественные объекты, была вам интересна и не так сложна для восприятия как могло показаться. Желаю вам бесконечной удачи в ваших начинаниях, будьте свободными от ограничений восприятия и позвольте себе делать больше активности в изученном направлени . Надеюсь, что теперь ты понял что такое естественные объекты, автомат с линейной тактикой, доверчивый автомат, автомат кринского, осторожный автомат крылова, коллектив автоматов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Искусственный интеллект

Механизмы обучения. Естественные объекты. Автомат с линейной тактикой. Доверчивый (автомат Кринского). Осторожный Крылова. Коллектив автоматов

рис.3.3

осторожный автомат крылова

Какая глубина лучше?

Коллектив автоматов

Вау!! 😲 Ты еще не читал? Это зря!

Комментарии

Оставить комментарий

Искусственный интеллект

Термины: Искусственный интеллект