Лекция
Привет, Вы узнаете о том , что такое модель акторов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое модель акторов, математическая модель параллельных вычислений , настоятельно рекомендую прочитать все из категории Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы.
В компьютерных науках модель акторов представляет собой математическую модель параллельных вычислений, которая трактует понятие «актор» как универсальный примитив параллельного численного расчета: в ответ на сообщения, которые он получает, актор может принимать локальные решения, создавать новые акторы, посылать свои сообщения, а также устанавливать, как следует реагировать на последующие сообщения. Модель акторов возникла в 1973 году. Она использовалась как основа для понимания исчисления процессов и как теоретическая база для ряда практических реализацийпараллельных систем.
В отличие от предыдущих моделей вычислений, появление модели акторов было стимулировано физикой, в том числе общей теорией относительности и квантовой механикой. На процесс формирования модели оказали также влияние языки программирования Lisp, Симула и ранние версии Smalltalk, а также методы параметрической защиты и коммутации пакетов. Развитие модели было «мотивировано перспективой высокопараллельных вычислительных машин, состоящих из десятков, сотен и даже тысяч независимых микропроцессоров, каждый со своей собственной локальной памятью и коммуникационным процессором, общающихся через сеть высокопроизводительной связи». С массовым распространением параллелизма, возникшего благодаря развитию многоядерных архитектур, интерес к модели акторов значительно возрос.
После публикации Хьюитта, Бишопа и Штайгера в 1973 г. Ирен Грейф разработала операционную семантику для модели акторов как часть своей докторской диссертации. Два года спустя Генри Бейкер и Хьюитт опубликовали множество аксиоматических законов для систем акторов. Другие значимые вехи включают диссертацию Уильяма Клингера в 1981 году, представившего денотативную семантику, основанную на мощности доменов, и диссертацию Гуля Ага 1985 г., в которой дано дальнейшее развитие семантической модели Клингера. В результате этих работ теория модели акторов получила полное развитие.
Модель акторов исходит из такой философии, что все вокруг является акторами. Это похоже на философию объектно-ориентированного программирования, где все вокруг является некоторыми объектами, но отличается тем, что в объектно-ориентированном программировании программы, как правило, выполняются последовательно, в то время как в модели акторов вычисления по своей сути совпадают по времени.
Актор является вычислительной сущностью, которая в ответ на полученное сообщение может одновременно:
Может существовать произвольная последовательность вышеописанных действий, и все они могут выполняться параллельно.
Развязка отправителя и посланных сообщений стала фундаментальным достижением модели акторов, обеспечившая асинхронную связь и управление структурами как прототип передачи сообщений.
Получатели сообщений идентифицируются по адресу, который иногда называют «почтовым адресом». Таким образом, актор может взаимодействовать только с теми акторами, адреса которых он имеет. Он может извлечь адреса из полученных сообщений или знать их заранее, если актор создан им самим.
Модель акторов характеризуется внутренне присущим параллелизмом вычислений внутри одного актора и между ними, динамическое создание акторов, включение адресов акторов в сообщения, а также взаимодействие только через прямой асинхронный обмен сообщениями без каких-либо ограничений на порядок прибытия сообщений.
За прошедшие годы были разработаны несколько различных формальных систем, которые позволяют описать модели акторов. К ним относятся:
Есть также формализмы, которые не полностью соответствуют модели акторов в том аспекте, что они не формализуют гарантированную доставку сообщений. К ним, в частности, относятся:
Модель акторов может быть использована в качестве основы для моделирования, понимания и аргументации по широкому спектру параллельных систем, например:
Модель акторов сформировалась на базе предшествующих моделей вычислений.
Лямбда-исчисление Алонзо Черча можно рассматривать как самый первый язык программирования обмена сообщениями. (см. Абельсон и Суссман 1985). Например, нижеприведенное лямбда-выражение реализует древовидную структуру данных, если оно используется с параметрами leftSubTree и rightSubTree. Если на входе такого дерева дать в качестве параметра сообщение "getLeft", оно возвратит leftSubTree, а если дать сообщение "getRight", то возвратится rightSubTree.
λ(leftSubTree,rightSubTree)
λ(message)
if (message == "getLeft") then leftSubTree
else if (message == "getRight") then rightSubTree
Семантика лямбда-исчислений выражается при помощи подстановок переменных, в которых значения параметров заменяются в теле вызываемых лямбда-выражений. Модель подстановок непригодна для параллелизма, поскольку она не обеспечивает возможность совместного использования ресурсов. Под влиянием лямбда-исчислений интерпретатор языка программирования Lisp использует структуры данных, называемые средой (environment ), такие, что значения параметров не должны заменяться в теле запускаемых лямбда-выражений. Это обеспечивает совместное использование эффектовобновления общих структур данных, но не обеспечивает параллелизм.
Язык Симула был пионером в использовании передачи сообщений для вычислений, связанных с дискретными приложениями моделирования событий. В предыдущих языках моделирования эти приложения были громоздкими и немодульными. На каждом шаге времени нужно было выполнять большую центральную программу и обновлять состояния каждого моделируемого объекта, зависящие от состояния других объектов, с которыми данный объект взаимодействовал на текущем шаге моделирования. Кристен Нюгорд и Оле-Йохан Даль первыми развили идею (впервые изложена на семинаре IFIP в 1967 г.) применения методов, встроенных в каждый объект, которые обновляют свои собственные состояния на основании сообщений от других объектов. Кроме того, они ввели структуры классов для объектов с наследованием. Их нововведения значительно повысили модульность программ.
Однако в Симуле вместо истинного параллелизма использовались сопрограммы управления структурами.
При разработке Smalltalk-71 Алан Кэй находился под влиянием возможности передачи сообщений в управляемых шаблонами вызовах языка Planner. Хьюитт был заинтригован языком Smalltalk-71, но отложил его применение из-за сложности коммуникаций, которые включают вызовы со многими полями, включая global, sender, receiver, reply-style, status, reply, operator selector и т.д.
В 1972 году Кэй посетил MIT и обсудил некоторые свои идеи для Smalltalk-72, основанные на возможностях языка программирования Лого Сеймура Паперта и на модели вычислений «маленький человек», используемой для обучения детей программированию. Однако, передача сообщений в Smalltalk-72 была довольно сложной. Код на языке рассматривался интерпретатором просто как поток символов. Как позже писал Дэн Инголс:
Первый встретившийся в динамическом контексте символ в программе использовался для определения получателя последующего сообщения. Поиск имени начинался с типа словаря в текущей активации. В случае ошибки сообщение перенаправлялось создателю активации, и так далее по цепочке, вплоть до отправителя сообщения. Когда связывание, наконец, находило символ, его значение присваивалось получателю нового сообщения, а интерпретатор активировал код для класса этого объекта.
Таким образом, передача сообщений в Smalltalk-72 была тесно привязана к конкретной модели машины и к синтаксису языка программирования, который не был приспособлен для параллелизма. Кроме того, хотя система загружалась сама, языковые конструкции не были формально определены как объекты, которые отвечают на Eval сообщения (см. обсуждение ниже). Это позволило некоторым сделать вывод, что новая математическая модель параллельных вычислений на основе передачи сообщений должна быть проще, чем Smalltalk-72.
Последующие версии языка Smalltalk в значительной степени развивались по пути использования виртуальных методов из языка Симула в структурах программ передачи сообщений. Об этом говорит сайт https://intellect.icu . Однако в Smalltalk-72 в объектах появились примитивы, таких как целые числа, числа с плавающей точкой, и т.д. Авторы языка Симула рассмотрели принятие таких примитивов в объектах, но воздержались от этого, в основном по соображениям эффективности. В языке Javaсначала посчитали целесообразным использовать как примитивы, так и версии объектов целых чисел, чисел с плавающей точкой, и др. В языке программирования C# (и более поздних версиях Java, начиная с Java 1.5) принято менее элегантное решение использования упаковки и распаковки, которые ранее использовались в некоторых реализациях Lisp.
Система Smalltalk впоследствии стала очень популярной и влиятельной, оказав инновационное воздействие на растровые дисплеи, персональные компьютеры, интерфейс браузеров и на многое другое.[12] Тем временем усилия разработчиков модели акторов в MTI сосредоточились на развитии научных и технических основ более высокого уровня параллелизма.
До появления модели акторов сети Петри широко использовались для моделирования недетерминированных вычислений. Однако, было признано, что они имеют важное ограничение: они моделируют управление потоком, но не сам поток данных. Следовательно, они не были легко компонуемыми, что тем самым ограничивало их модульность. Хьюитт отметил еще одну проблему сетей Петри: сложность одновременных действий. Элементарный шаг вычислений в сети Петри представляет собой переход, при котором токены одновременно исчезают на входах перехода и появляются на его выходах. Физические основы использования примитивов с такого рода одновременностью оказались сомнительными. Несмотря на эти очевидные трудности, метод сетей Петри остается популярным подходом к моделированию параллелизма, и все еще является предметом активных исследований.
До модели акторов параллелизм был определен в аппаратных терминах низкого уровня через нити, блокировки и буферы (каналы). Не случайно, конечно, то, что реализация модели акторов обычно использует эти аппаратные возможности. Однако, нет никаких оснований считать, что модель не может быть реализована непосредственно в аппаратуре без эквивалентных аппаратных нитей и блокировок. Кроме того, нет обязательной связи между акторами, нитями и блокировками, которые могут быть вовлечены в вычисления. Реализации модели акторов не связаны непосредственно с нитями и блокировками во всех случаях, совместимых с законами для акторов.
Вот что можно сказать относительно семантики передаваемых сообщений в модели акторов.
Возможно, первыми параллельными программами были обработчики прерываний. В процессе работы, как правило, компьютеру необходимо реагировать на внешние события, которые могут происходить в заранее неизвестный момент времени (асинхронно, по отношению к выполняющейся в данный момент программе) - например, получать информацию извне (символы с клавиатуры, пакеты из сети и т.д.). Наиболее эффективно обработка таких событий реализуется с помощью т.н. прерываний - когда происходит событие, выполнение текущей программы «прерывается» и запускается обработчик прерывания, который выполняет небходимые для реакции на событие действия (например, получает поступающую информацию и сохраняет ее в буфер, откуда она может быть впоследствии считана), после чего основная программа продолжает свою работу с того места, где она была прервана.
В начале 1960-х прерывания стали использовать для имитации одновременного выполнения нескольких программ на одном процессоре.[13] Наличие параллелизма с общей памятью привело к проблеме управления параллелизмом. Первоначально эта задача задумывалась как один из мьютексов на отдельном компьютере. Эдсгер Дейкстра разработал семафоры, а позднее, в период между 1971 и 1973 годах, Чарльз Хоар и Пер Хансен для решения проблемы мьютексов разработали мониторы.[14][15][16] Однако, ни одно из этих решений не создавало в языках программирования конструкций, которые бы инкапсулировали доступ к совместным ресурсам. Инкапсуляцию сделали позже Хьюитт и Аткинсон, построив параллельно-последовательный преобразователь ([Hewitt, Atkinson 1977, 1979] и [Atkinson 1980]).
Первые модели вычислений (например, машина Тьюринга, машина Поста, лямбда-исчисление и т.д.) были основаны на математике и использовали понятие глобального состояния, чтобы определить шаг вычисления (позднее эти понятия обобщены в работах [McCarthy and Hayes 1969] и [Dijkstra 1976]). Каждый шаг вычисления шел от одного глобального состояния вычислений до следующего. Глобальный подход к состоянию был продолжен в теории автоматов для конечных автоматов и машин со стеком, в том числе их недетерминированные версии. Такие недетерминированные автоматы имеют свойство ограниченного индетерминизма. То есть, если машина всегда стоит перед тем, как она переходит в исходное состояние, то имеется ограничение на число состояний, в которых она может находиться.
Эдсгер Дейкстра развил дальше подход с недетерминированными глобальными состояниями. Модель Дейкстры породила споры о неограниченном индетерминизме. Неограниченный индетерминизм (называемый также неограниченным недетерминизмом) является свойством одновременных вычислений, при котором величина задержки в обслуживании запроса может стать неограниченной в результате арбитражного соперничества за общие ресурсы, в то же время гарантируется, что запрос в конечном итоге будет обслужен. Хьюитт утверждает, что модель акторов должна обеспечить гарантии на предоставление услуги. Хотя в модели Дейкстры не может быть неограниченного количества времени между выполнением последовательных операций на компьютере, параллельно выполняемая программа, которая начала свою работу в строго определенном состоянии, может быть прервана лишь в ограниченном числе состояний [Dijkstra 1976]. Следовательно, модель Дейкстры не может обеспечить гарантии предоставления услуги. Дейкстра утверждал, что невозможно осуществить неограниченный индетерминизм.
Хьюитт утверждал иное: не существует ограничения на время, которое затрачивается на работу участка вычислений, называемого арбитром для урегулирования конфликтов. Арбитры имеют дело с разрешением таких ситуаций. Часы компьютера работают асинхронно с внешними входами: вводом с клавиатуры, доступом к диску, сетевым входом и т.д. Так что для получения сообщения, отправленного на компьютер, может пройти неограниченное время, и за это время компьютер может пройти через неограниченное количество состояний.
Неограниченный индетерминизм является характерной чертой модели акторов, в которой используется математическая модель Билла Клингера, основанная на теории доменов. В модели акторов не существует глобального состояния.
Сообщения в модели акторов не обязательно буферизуются. В этом ее резкое различие с предшествующими подходами к модели одновременных вычислений. Отсутствие буферизации вызвало большое недоразумение во время развития модели акторов, и до сих пор эта тема является предметом споров. Некоторые исследователи утверждают, что сообщения буферизуются в «эфире» или «окружающей среде». Кроме того, сообщения в модели акторов просто посылаются (например, пакеты в IP). Никаких требований на синхронное рукопожатие с получателем не существует.
Естественным развитием модели акторов была возможность передачи адресов в сообщениях. Под влиянием сетей с коммутацией пакетов Хьюитт предложил разработать новую модель одновременных вычислений, в которой связь не будет иметь вообще никаких обязательных полей, все они могут быть пустыми. Конечно, если отправитель сообщения желает, чтобы получатель имел доступ к адресам, которых он еще не имеет, адрес должен быть отправлен в сообщении.
В процессе вычислений, возможно, потребуется отправить сообщение получателю, от которого позже нужно получить ответ. Способ сделать это состоит в том, чтобы отправить сообщение, в котором записан адрес другого актора, называемого возобновлением (иногда его также называют продолжением илистеком вызовов). Получатель может затем сделать ответное сообщение, которое будет отправлено на возобновление.
Создание акторов плюс включение адресов участников в сообщения означает, что модель акторов имеет потенциально переменную топологию в своих отношениях друг с другом, походя на объекты в языке Симула, которые в своих отношениях друг с другом также имеют переменную топологию.
В отличие от предыдущего подхода, основанного на комбинировании последовательных процессов, модель акторов была разработана как одновременная модель по своей сути. Как написано в теории моделей акторов, последовательность в ней представляет собой особый случай, вытекающий из одновременных вычислений.
Хьюитт был против включения требований о том, что сообщения должны прибывать в том порядке, в котором они отправлены на модель актора. Если желательно упорядочить входящие сообщения, то это можно смоделировать с помощью очереди акторов, которая обеспечивает такую функциональность. Такие очереди акторов упорядочивали бы поступающие сообщения так, чтобы они были получены в порядке FIFO. В общем же случае, если актор Xотправляет сообщение M1 актору Y, а затем тот же актор X отправляет другое сообщение M2 к Y, то не существует никаких требований о том, что M1 придет кY раньше M2.
В этом отношении модель акторов зеркально отражает систему коммутации пакетов, которая не гарантирует, что пакеты будут получены в порядке отправления. Отсутствие гарантий порядка доставки сообщений позволяет системе коммутации пакетов буферизовать пакеты, использовать несколько путей отправки пакетов, повторно пересылать поврежденные пакеты и использовать другие методы оптимизации.
Например, акторы могут использовать конвейер обработки сообщений. Это означает, что в процессе обработки сообщения M1 актор может варьировать поведение, которое будет использоваться для обработки следующего сообщения. В частности, это означает, что он может начать обработку еще одного сообщения M2 до завершения обработки M1. На том основании, что актору предоставлено право использования конвейера обработки сообщений, еще не означает, что он этот конвейер обязан использовать. Будет ли сообщение конвейеризовано или нет — относится к задачам технического компромисса. Как внешний наблюдатель может узнать, что обработка сообщения актора прошла через конвейер? На этот счет не существует никакой двусмысленности в отношении применения актором возможности конвейеризации. Только если в конкретной реализации выполнение конвейерной оптимизации сделано неправильно, в этом случае может произойти не ожидаемое поведение, а нечто другое.
Другой важной характеристикой модели акторов является локальность. Локальность означает, что при обработке сообщения актор может отправлять сообщения только по тем адресам, которые он получил из этого сообщения, по адресам, которые он уже имел до получения сообщения, и по адресам, которые он создал при обработке сообщения.
Локальность также означает, что не может одновременно произойти несколько изменений адресов. В этом отношении модель акторов отличается от некоторых других моделей параллелизма, например, от сетей Петри, в которых реализации одновременно могут быть удалены из нескольких позиций и размещены по другим адресам.
Идея композиции систем акторов в более крупные образования является важным аспектом модульности, которая была разработана в докторской диссертации Гуля Ага , позже развитой им же вместе с Ианом Мейсоном, Скоттом Смитом и Каролин Талкотт.
Основным новшеством модели акторов было введение понятия поведения, определенное как математическая функция, выражающая действия актора, когда он обрабатывает сообщения, включая определение нового поведения на обработку следующего поступившего сообщения. Поведение обеспечивает функционирование математической модели параллелизма.
Поведение также освобождает модель акторов от деталей реализации, как, например, в Smalltalk-72 это делает маркер интерпретатора потока. Однако, важно понимать, что эффективное внедрение систем, описываемых моделью акторов, требует расширенную оптимизацию.
Другие системы параллелизма (например, исчисление процессов) могут быть смоделированы в модели акторов с использованием двухфазного протокола фиксации.[17]
В модели акторов существует теорема вычислительных представлений для замкнутых систем, в том смысле, что они не получают сообщений извне. В математической записи замкнутая система, обозначаемая как S, строится как наилучшее приближение для начального поведения, называемого ⊥S, с использованием аппроксимирующей функции поведения progressionS, построенной для S следующим образом (согласно публикации Хьюитта 2008 г.):
DenoteS ≡ ⊔i∈ω progressionSi(⊥S)
Таким образом, S может быть математически охарактеризована в терминах всех его возможных поведений (в том числе с учетом неограниченного индетерминизма). Хотя DenoteS не является реализацией S, она может быть использована для доказательства обобщения тезиса Черча-Тьюринга-Россера-Клини (см. Клини, 1943):
Теорема перечислимости: если примитив актора замкнутой системы акторов являются эффективным, то его возможные выходы рекурсивно перечислимы.
Доказательство: непосредственно вытекает из теоремы вычислительных представлений.
Развитие модели акторов имеет интересную связь с математической логикой. Одной из ключевых мотиваций для ее развития была необходимость управления аспектами, которые возникли в процессе развития языка программирования Planner. После того как модель акторов была первоначально сформулирована, стало важно определить мощность модели в отношении тезиса Роберта Ковальского о том, что «вычисления могут быть сгруппированы по логическим выводам». Тезис Ковальского оказался ложным для одновременных вычислений в модели акторов. Этот результат все еще является спорным, и он противоречит некоторым предыдущим представлениям, поскольку тезис Ковальского верен для последовательных вычислений и даже для некоторых видов параллельных вычислений, например, для лямбда-исчислений.
Тем не менее были предприняты попытки расширения логического программирования для одновременных вычислений. Однако, Хьюитт и Ага в работе 1999 г. утверждают, что результирующая система не является дедуктивной в следующем смысле: вычислительные шаги параллельных систем программирования логики не следуют дедуктивно из предыдущих шагов.
Миграцией в модели акторов называется способность актора изменить свое местоположение. Например, Аки Йонезава в своей диссертации моделировал почтовую службу, в которой акторы-клиенты могли войти, изменить местоположение во время работы и выйти. Актор, который мог мигрировать, моделировался как актор с определенным местом, изменяющемся при миграции актора. Однако достоверность этого моделирования является спорной и служит предметом исследований.
Безопасность акторов может быть обеспечена одним из следующих способов:
Тонким моментом в модели акторов является возможность синтеза адреса актора. В некоторых случаях система безопасности может запрещать синтез адресов. Поскольку адрес актора это просто битовая строка, то, очевидно, его можно синтезировать, хотя, если битовая строка достаточно длинная, подобрать адрес актора довольно трудно или даже невозможно. SOAP в качестве адреса конечной точки использует URL, по которому актор расположен. Так как URL является строкой символов, то, очевидно, ее можно синтезировать, хотя если применить шифрование, то подобрать строку практически невозможно.
Синтезирование адресов акторов обычно моделируются с помощью отображения. Идея состоит в использовании системы акторов для выполнения отображения на фактические адреса акторов. Например, структура памяти компьютера может быть смоделирована как система акторов, которая дает отображение. В случае адресов SOAP это моделирование DNS и отображение URL.
Первая из опубликованных работ Робина Милнера о параллелизме[18] была примечательна тем, что она не была основана на композиции последовательных процессов. Его работа отличалась от модели акторов, потому что она была основана на фиксированном количестве процессов фиксированного числа связей в топологии строк, используемых для синхронизации связи. Оригинальная модель взаимодействующих последовательных процессов (CSP), опубликованная Энтони Хоаром[19], отличается от модели акторов, потому что она основана на параллельной композиции фиксированного числа последовательных процессов, связанных в фиксированную топологию и общающихся с помощью синхронной передачи сообщений на основе имен процессов. Более поздние версии CSP отказались от связи на основе имен процессов, приняв принцип анонимной связи по каналам. Этот подход используется также в работе Милнера об исчислении общающихся систем и пи-исчислении.
Этим обеим ранним моделям Милнера и Хоара свойствен ограниченный индетерминизм. Современные теоретические CSP ([Hoare 1985] и [Roscoe 2005]) прямо предусматривают неограниченный индетерминизм.
Через сорок лет после публикации закона Мура продолжающееся возрастание производительности микросхем происходит благодаря методам локального и глобального массового параллелизма. Локальный параллелизм задействован в новых микросхемах для 64-разрядных многоядерных микропроцессоров, в мульти-чиповых модулях и высокопроизводительных системах связи. Глобальный параллелизм в настоящее время задействован в новом оборудовании для проводной и беспроводной широкополосной пакетной коммутации сообщений (см. Wi-Fi и Ultra Wideband). Ёмкость хранения за счет как локального, так и глобального параллелизма, растет в геометрической прогрессии.
По словам Хьюитта (см. Carl Hewitt, 2006a), модель акторов ставит вопросы в области компьютеров и архитектуры связи, языков параллельного программирования и веб-сервисов, включая следующие:
Многие идеи, введенные в модели акторов, в настоящее время находят также применение в многоагентных системах по этим же причинам (см. Хьюитт, 2006b, 2007b). Ключевым отличием является то, что агент системы (в большинстве определений) накладывает дополнительные ограничения на акторов, как правило, требуя, чтобы они использовали обязательства и цели.
Модель акторов применяется также в клиентах облачных вычислений.[20]
Ранние программные языки с акторами Большое число различных языков программирования используют модель акторов или ее варианты. Среди них:
Разработаны библиотеки и табличные структуры с акторами для обеспечения актороподобного стиля программирования на языках, которые не имеют встроенных акторов.
Высокий параллелизм、распределенныйИ инструментарий и время выполнения отказоустойчивых приложений, вы можете понять, что Akka является основой для написания параллельных программ.Scalaс участиемJavaРазработка интерфейса.Решения для одновременных проблем,Очень хорошо!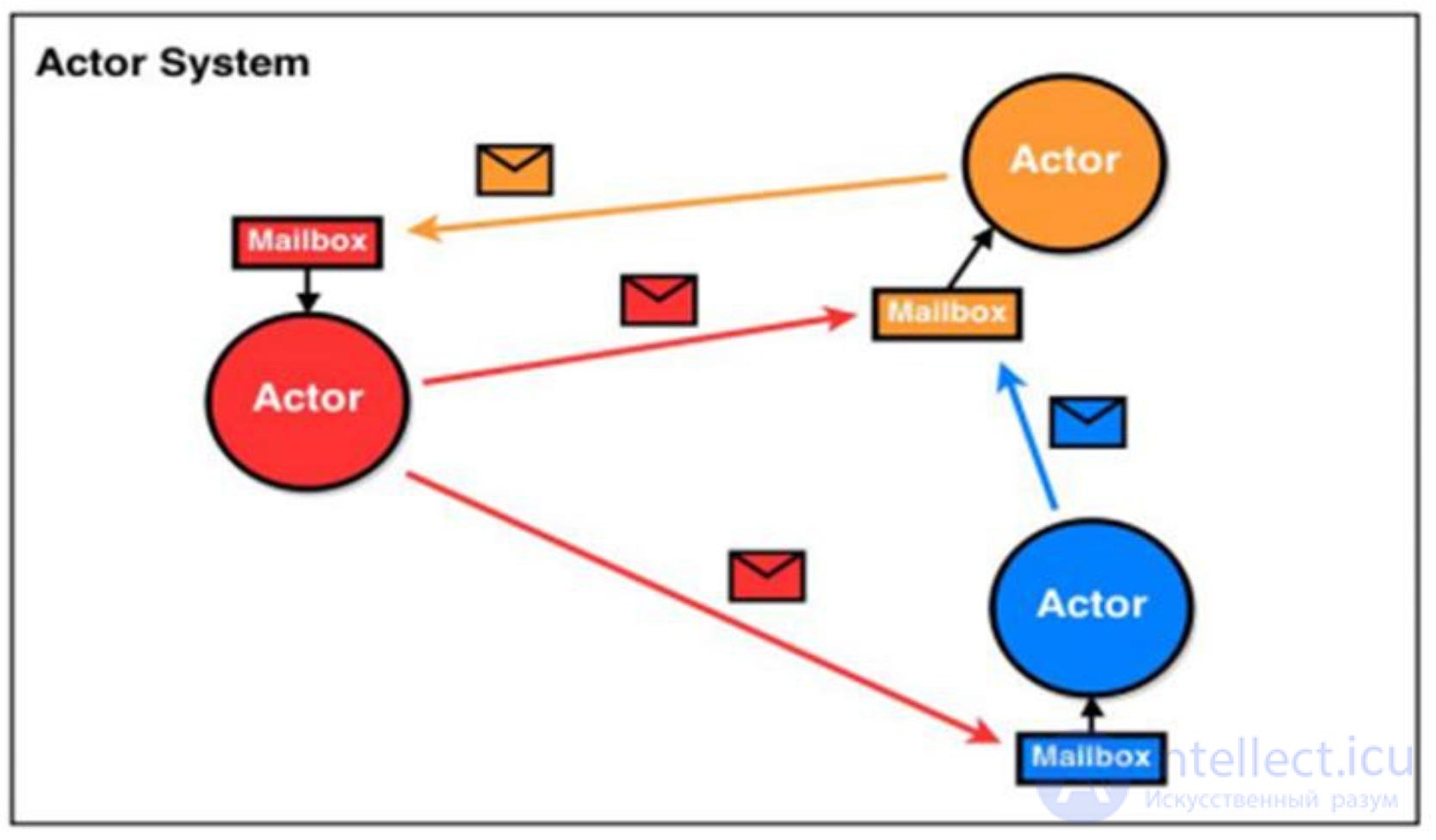
В заключение, эта статья об модель акторов подчеркивает важность того что вы тут, расширяете ваше сознание, знания, навыки и умения. Надеюсь, что теперь ты понял что такое модель акторов, математическая модель параллельных вычислений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы
Термины: Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы