Топологические связи модулей Вычислительных систем для параллельных вычслений

Привет, сегодня поговорим про топологические связи модулей вычислительных систем для параллельных вычслений, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое топологические связи модулей вычислительных систем для параллельных вычслений , настоятельно рекомендую прочитать все из категории Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы.

Топологические связи модулей ВС

Выбор той топологии связи процессоров в конкретной вычислительной системе может быть обусловлен самыми разными причинами. Это могут быть соображениями стоимости, технологической реализуемости, простоты сборки и программирования, надежности, минимальности средней длины пути между узлами, минимальности максимального расстояния между узлами и др. 

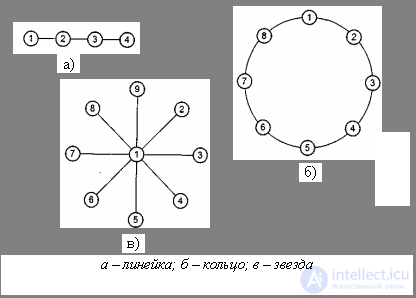
  Варианты топологий связи процессоров и ВМ NUMA Non Uniform Memory Access 

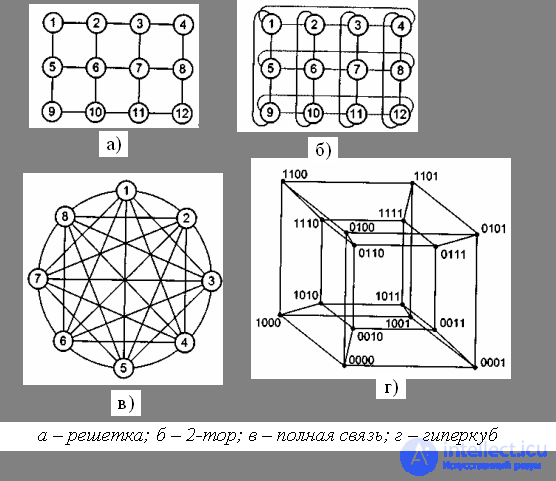
 Топология двоичного гиперкубы  

В n-мерном пространстве в вершинах единичного n- мерного куба размещаются процессоры системы, т. Об этом говорит сайт https://intellect.icu . е. точки (x 1, x 2, …, х n ), в которых все координаты х i могут быть равны либо 0, либо 1. Каждый процессор соединим с ближайшим непосредственным соседом вдоль каждого из n измерений. В результате получается n-мерный куб для системы из N = 2 n процессоров. Двумерный куб соответствует простому квадрату, а четырехмерный вариант условно изображен на рисунке. В гиперкубе каждый процессор связан лишь с log 2 N непосредственными соседями, а не с N, как в случае полной связности. Гиперкуб имеет массу полезных свойств. Например, для каждого процессора очень просто определить всех его соседей: они отличаются от него лишь значением какой-либо одной координаты х i. Каждая "грань" n-мерного гиперкуба является гиперкубом размерности n-1. Максимальное расстояние между вершинами n-мерного гиперкуба равно n. Гиперкуб симметричен относительно своих узлов: из каждого узла система выглядит одинаковой и не существует узлов, которым необходима специальная обработка. 

В общем, мой друг ты одолел чтение этой статьи об топологические связи модулей вычислительных систем для параллельных вычслений. Работы впереди у тебя будет много. Смело пиши комментарии, развивайся и счастье окажется в твоих руках. Надеюсь, что теперь ты понял что такое топологические связи модулей вычислительных систем для параллельных вычслений и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Высоконагруженные проекты.Паралельные вычисления. Суперкомпьютеры. Распределенные системы