Лекция
Привет, Вы узнаете о том , что такое машина тьюринга, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое машина тьюринга, классификация машин тьюринга , настоятельно рекомендую прочитать все из категории Теория конечных автоматов.
машина тьюринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Черча — Тьюринга, способна имитировать всех исполнителей (с помощью задания правил перехода), каким-либо образом реализующих процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
То есть всякий интуитивный алгоритм может быть реализован с помощью некоторой машины Тьюринга .
В своем эссе 1948 года «Интеллектуальные машины» Тьюринг писал, что его машина состоит из:
... неограниченный объем памяти, полученный в виде бесконечной ленты, размеченной квадратами, на каждом из которых может быть напечатан символ. В любой момент в автомате есть один символ; он называется отсканированным символом. Машина может изменять отсканированный символ, и его поведение частично определяется этим символом, но символы на ленте в другом месте не влияют на поведение машины. Однако ленту можно перемещать вперед и назад через машину, что является одной из элементарных операций машины. Следовательно, у любого символа на ленте может быть иннингс. [18]
- Тьюринг 1948, стр. 3
По сути своей, алгоритм есть механический процесс обработки информации. При выполнении алгоритма в интуитивном смысле мы можем пользоваться потенциально неограниченной памятью, запоминая в процессе выполнения алгоритма по мере необходимости нужную информацию, например, делая пометки на листочке бумаги. В то же время основным ограничением конечного автомата является конечность числа его состояний, а значит, его памяти. Можно предположить, что именно поэтому конечный автомат не может быть использован как модель устройства, выполняющего произвольные алгоритмы.
Следуя Hopcroft & Ullman (1979 , p. 148) , (однопленочная) машина Тьюринга может быть формально определена как кортеж из семи элементов. где
Относительно необычный вариант позволяет "без сдвига", скажем, N, в качестве третьего элемента набора направлений. .
Кортеж из 7 занятых бобров с 3 состояниями выглядит так (подробнее об этом занятом бобре см. В примерах машины Тьюринга ):
Изначально все ячейки ленты отмечены значком .
| Лента символ | Текущее состояние A | Текущее состояние B | Текущее состояние C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Написать символ | Переместить ленту | Следующее состояние | Написать символ | Переместить ленту | Следующее состояние | Написать символ | Переместить ленту | Следующее состояние | |
| 0 | 1 | р | B | 1 | L | А | 1 | L | B |
| 1 | 1 | L | C | 1 | р | B | 1 | р | HALT |
По словам ван Эмде Боаса (1990), стр. Об этом говорит сайт https://intellect.icu . 6: «Теоретико-множественный объект [его формальное описание из семи кортежей, подобное приведенному выше] предоставляет только частичную информацию о том, как машина будет вести себя и как будут выглядеть ее вычисления».
Например,
Если к модели КА добавить способность запоминания произвольно больших объемов информации, то его возможности по выполнению алгоритмов расширятся и мы получим автомат с более широкими возможностями по преобразованию информации. Алан Тьюринг в 1936 году определил понятие алгоритма, исходя из понятия автоматически работающей машины, и предложил формальную модель вычислителя, которая является результатом простого добавления потенциально бесконечной памяти к конечному автомату. Он предложил формальную модель такого устройства, которое моделирует действия человека, решающего задачу, руководствуясь некоторым алгоритмом. Это устройство было названо машиной Тьюринга.
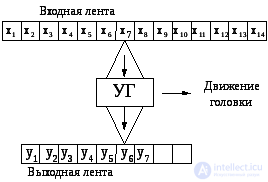
Рис.6.3
Рассмотрим, чем отличается машина Тьюринга от простой модели конечного автомата. Конечный автомат можно представить себе как устройство с конечным числом внутренних состояний Q = {q1, q2, …, qk }, работающее с двумя лентами: входной с конечным алфавитом X = {x1, x2, …, xn} и выходной с конечным алфавитом Y = {y1, y2,…, ym} (рис. 6.3). Конечный автомат работает по тактам. На каждом такте он читает с помощью некоторой входной головки символ из обозреваемой ячейки входной ленты, изменяет свое состояние и печатает некоторый символ выходного алфавита в обозреваемую ячейку выходной ленты, после чего две его головки чтения и записи перемещаются на одну позицию вправо. Описание функционирования конечного автомата можно считать его программой, которая является фактически перечислением аргументов и соответствующих значений частично-определенной функции переходов и выходов автомата δ: Q×X→ Q'×Y.
Человек имеет конечную память, и в этом смысле его можно представить системой с конечным числом состояний. Исходная информация к алгоритму обычно представляется в виде конечной последовательности символов (в виде слова конечного словаря). Выполняя алгоритм, человек-вычислитель использует дополнительную память (которая может быть потенциально бесконечной, например листы бумаги) для записи информации, причем эта запись производится им последовательно, символ за символом. При вычислениях человек может возвращаться к ранее записанной информации, стирать некоторую информацию и т. д. Таким образом, элементарными операциями при выполнении алгоритма можно считать запись и стирание символа, а также перенесение внимания с одного участка записи на другой.
Предложенная Тьюрингом формальная модель состоит: 1) из управляющего устройства, которое может находиться в одном из состояний, образующих конечное множество Q = {q1, q2, …, qk }; 2) ленты, разбитой на ячейки, в каждой из которых могут быть записаны символы конечного алфавита X = {x1, x2, …, xn}; 3) устройства обращения к ленте, т. е. считывающей и пишущей головки, которая сдвигается на ячейку влево или вправо или остается на месте. Предложенная Тьюрингом формальная модель отличается от конечного автомата в двух аспектах: она имеет одну бесконечную рабочую ленту, с которой читает и куда пишет символы, и головку чтения-записи, которая может двигаться по рабочей ленте в любую сторону (см. рис. 6.4).
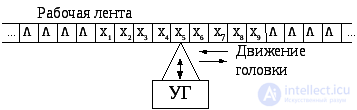
Рис.6.4
В каждой ячейке неограниченной ленты может храниться только один символ алфавита X, называемый внешним алфавитоммашины. Работа машины происходит по тактам. На каждом такте обозревается единственная ячейка и считываемый символ хiзаменяется другим хj, который определяется состоянием машины qv в данный тактовый момент из множества ее возможных состояний Q (при этом i = j означает, что символ не изменяется; стирание символа будем понимать как запись пустого символа Λ). Кроме того, вырабатывается последующее состояние машины qv+1 и управляющая перемещением по ленте команда,, которая подготавливает очередную ячейку для обозрения на следующем такте. Таких команд в машине Тьюринга только три: R – обозревать соседнюю справа ячейку, L – обозревать соседнюю слева ячейку и E – продолжать обозревать прежнюю ячейку. Совокупность символов Q = {q1, q2, …, qk } и D = {R, L, E} образует внутренний алфавит машины. Среди состояний управляющего устройства МТ следует выделить начальное состояние q1 и заключительное стоп-состояние, которое будем обозначать символом «!». В начальном состоянии машина находится перед началом работы; попав в заключительное состояние, машина останавливается.
Описание функционирования МТ можно считать ее программой, которая представлена конечным набором аргументов и соответствующих им значений частично-определенной функции переходов и выходов δ: Q×Х→ Q'×Х'×D.
Машина Тьюринга имеет один конечный рабочий алфавит Х, в котором входные и выходные символы не различаются, поскольку выходной символ, напечатанный на ленте, машина может прочитать в последующих тактах. Для удобства обычно считают, что алфавит Х также содержит и пустой символ Λ, заполняющий все ячейки рабочей ленты слева и справа от конечной цепочки «значащих» символов в начале работы.
Полное состояние машины Тьюринга, по которому однозначно можно определить ее дальнейшее поведение, определяется ее внутренним состоянием, состоянием ленты (т. е. словом, записанным на ленте) и положением головки на ленте. Полное состояние будем называть конфигурацией, или машинным словом, и обозначать тройкой α1 qv α2, где qv – текущее внутреннее состояние, α1 – слово слева от головки, а α2 – слово, образованное символом, считываемым головкой, и символами справа от него, причем слева от α1 и справа от α2 все ячейки ленты заполнены пустыми символами Λ.
Существуют различные модификации и обобщения машины Тьюринга; к ним относятся, в частности, многоленточные и многоголовочные машины, а также машины с различными ограничениями возможностей передвижения головки и преобразования информации на ленте.
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
Попытка классификации машин Тьюринга, предпринята В.А. Успенским и А.Л. Семеновым [1987, с. 238–243]. Следуя ей, изобразим следующую классификационную схему:

По отношению к случайности
По количеству лент
По своству ленты
По размерности
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте (то есть на ленте, бесконечной в одну сторону).
Рассмотрим доказательство, приведенное Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых, произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:

Затем перенумеруем ячейки, причем будем считать, что символ «*» не содержится в словаре МТ:

Наконец, изменим машину Тьюринга, удвоив число ее состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна ее работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:
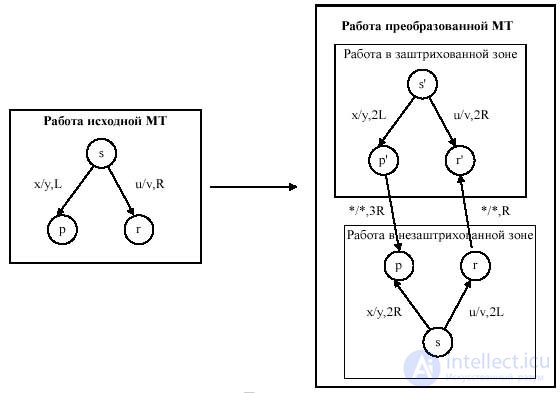
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
Часто говорят , что машины Тьюринга, в отличие от более простых автоматов, столь же мощны, как и настоящие машины, и способны выполнять любую операцию, которую может выполнять настоящая программа. В этом утверждении пренебрегают тем, что, поскольку реальная машина может иметь только конечное число конфигураций , эта «настоящая машина» на самом деле не что иное, как конечный автомат . С другой стороны, машины Тьюринга эквивалентны машинам, у которых есть неограниченный объем памяти для своих вычислений.
Есть несколько способов объяснить, почему машины Тьюринга являются полезными моделями реальных компьютеров:
Ограничение машин Тьюринга состоит в том, что они плохо моделируют сильные стороны конкретной системы. Например, современные компьютеры с хранимой программой на самом деле являются экземплярами более конкретной формы абстрактной машины, известной как машина с хранимой программой с произвольным доступом или модель машины RASP. Подобно универсальной машине Тьюринга , RASP хранит свою «программу» в «памяти», внешней по отношению к «инструкциям» своего конечного автомата. В отличие от универсальной машины Тьюринга, RASP имеет бесконечное количество различимых, пронумерованных, но неограниченных «регистров» - «ячеек» памяти, которые могут содержать любое целое число (см. Элгот и Робинсон (1964), Хартманис (1971) и, в частности, Кука). -Rechow (1973); ссылки на машину с произвольным доступом). Конечный автомат RASP оборудован возможностью косвенной адресации (например, содержимое одного регистра может использоваться как адрес для указания другого регистра); таким образом, «программа» RASP может обращаться к любому регистру в последовательности регистров. Результатом этого различия является то, что существуют вычислительные оптимизации, которые могут быть выполнены на основе индексов памяти, что невозможно в обычной машине Тьюринга; таким образом, когда машины Тьюринга используются в качестве основы для ограничения времени работы, «ложная нижняя граница» может быть доказана на временах работы определенных алгоритмов (из-за ложного упрощающего предположения машины Тьюринга). Примером этого является бинарный поиск, алгоритм, который может работать быстрее при использовании модели вычислений RASP, а не модели машины Тьюринга.
На заре компьютерных технологий использование компьютеров обычно ограничивалось пакетной обработкой , то есть неинтерактивными задачами, каждая из которых производила выходные данные из заданных входных данных. Теория вычислимости, изучающая вычислимость функций от входов к выходам, и для которой были изобретены машины Тьюринга, отражает эту практику.
С 1970-х годов интерактивное использование компьютеров стало гораздо более распространенным. В принципе, это можно смоделировать, если внешний агент будет читать с ленты и записывать на нее одновременно с машиной Тьюринга, но это редко соответствует тому, как на самом деле происходит взаимодействие; поэтому при описании интерактивности обычно предпочтительны такие альтернативы, как автоматы ввода-вывода .
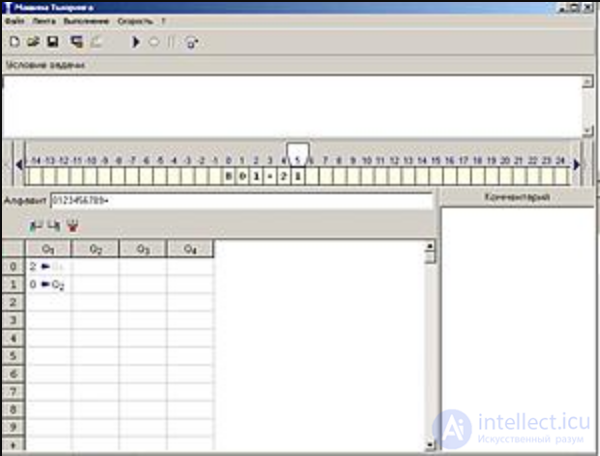
Построить Машину Тьюринга,которая может найти сумму чисел и ответ записать в десятичной системе счисления

Анализ данных, представленных в статье про машина тьюринга, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое машина тьюринга, классификация машин тьюринга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория конечных автоматов
Комментарии
Оставить комментарий
Теория конечных автоматов
Термины: Теория конечных автоматов