Лекция
Привет, Вы узнаете о том , что такое машина тьюринга детерминированная, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое машина тьюринга детерминированная, недетерминированная машина тьюринга, машина тьюринга , настоятельно рекомендую прочитать все из категории Теория автоматов.
Маши́на Тью́ринга (МТ) — абстрактный исполнитель (абстрактная вычислительная машина). Была предложена Аланом Тьюрингом в 1936 году для формализации понятия алгоритма.
Машина Тьюринга является расширением конечного автомата и, согласно тезису Черча — Тьюринга, способна имитировать все исполнители (с помощью задания правил перехода), каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
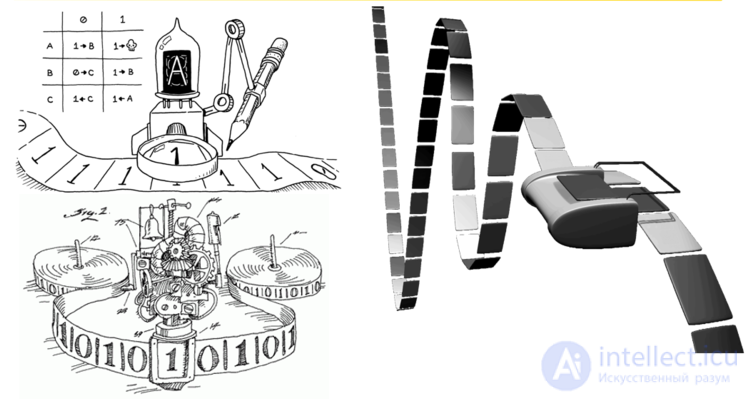
Художественное представление машины Тьюринга
В состав машины Тьюринга входит неограниченная в обе стороны лента (возможны машины Тьюринга, которые имеют несколько бесконечных лент), разделенная на ячейки, и управляющее устройство (также называется головкой записи-чтения (ГЗЧ)), способное находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано.
Управляющее устройство может перемещаться влево и вправо по ленте, читать и записывать в ячейки символы некоторого конечного алфавита. Выделяется особыйпустой символ, заполняющий все клетки ленты, кроме тех из них (конечного числа), на которых записаны входные данные.
Управляющее устройство работает согласно правилам перехода, которые представляют алгоритм, реализуемый данной машиной Тьюринга. Каждое правило перехода предписывает машине, в зависимости от текущего состояния и наблюдаемого в текущей клетке символа, записать в эту клетку новый символ, перейти в новое состояние и переместиться на одну клетку влево или вправо. Некоторые состояния машины Тьюринга могут быть помечены как терминальные, и переход в любое из них означает конец работы, остановку алгоритма.
Машина Тьюринга называется детерминированной, если каждой комбинации состояния и ленточного символа в таблице соответствует не более одного правила. Если существует пара «ленточный символ — состояние», для которой существует 2 и более команд, такая машина Тьюринга называется недетерминированной.
Конкретная машина Тьюринга задается перечислением элементов множества букв алфавита A, множества состояний Q и набором правил, по которым работает машина. Они имеют вид: qiaj→qi1aj1dk (если головка находится в состоянии qi, а в обозреваемой ячейке записана буква aj, то головка переходит в состояние qi1, в ячейку вместо aj записывается aj1, головка делает движение dk, которое имеет три варианта: на ячейку влево (L), на ячейку вправо (R), остаться на месте (N)). Для каждой возможной конфигурации i, aj> имеется ровно одно правило (для недетерминированной машины Тьюринга может быть большее количество правил). Правил нет только для заключительного состояния, попав в которое машина останавливается. Кроме того, необходимо указать конечное и начальное состояния, начальную конфигурацию на ленте и расположение головки машины.
Приведем пример МТ для умножения чисел в унарной системе счисления. Запись правила «qiaj→qi1aj1R/L/N» следует понимать так: qi — состояние при котором выполняется это правило, aj — данные в ячейке, в которой находится головка, qi1 — состояние в которое нужно перейти, aj1 — что нужно записать в ячейку, R/L/N — команда на перемещение.
Машина работает по следующему набору правил:
| q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | q01→q01R | q11→q2aR | q21→q21L | q31 → q4aR | q41→q41R | q71→q2aR | |||
| × | q0×→q1×R | q2×→q3×L | q4×→q4×R | q6×→q7×R | q8×→q9×N | ||||
| = | q2=→q2=L | q4=→q4=R | q7=→q8=L | ||||||
| a | q2a→q2aL | q3a→q3aL | q4a→q4aR | q6a→q61R | q7a→q7aR | q8a→q81L | |||
| * | q0*→q0*R | q3*→q6*R | q4*→q51R | ||||||
| q5 →q2*L |
Описание состояний:
| Начало | |
| q0 | начальное состояние. Ищем «x» справа. При нахождении переходим в состояние q1 |
|---|---|
| q1 | заменяем «1» на «а» и переходим в состояние q2 |
| Переносим все «1» из первого числа в результат | |
| q2 | ищем «х» слева. При нахождении переходим в состояние q3 |
| q3 | ищем «1» слева, заменяем ее на «а» и переходим в состояние q4.
В случае если «1» закончились, находим «*» и переходим в состояние q6 |
| q4 | переходим в конец (ищем «*» справа), заменяем «*» на «1» и переходим в состояние q5 |
| q5 | добавляем «*» в конец и переходим в состояние q2 |
| Обрабатываем каждый разряд второго числа | |
| q6 | ищем «х» справа и переходим в состояние q7. Об этом говорит сайт https://intellect.icu . Пока ищем заменяем «а» на «1» |
| q7 | ищем «1» или «=» справа
при нахождении «1» заменяем его на «а» и переходим в состояние q2 при нахождении «=» переходим в состояние q8 |
| Конец | |
| q8 | ищем «х» слева. При нахождении переходим в состояние q9. Пока ищем заменяем «а» на «1» |
| q9 | терминальное состояние (остановка алгоритма) |
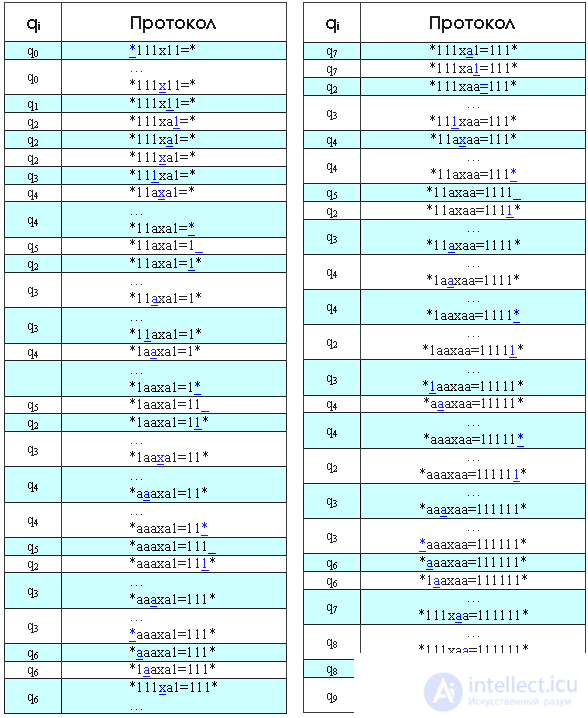
Умножим с помощью МТ 3 на 2 в единичной системе. В протоколе указаны начальное и конечное состояния МТ, начальная конфигурация на ленте и расположение головки машины (подчеркнутый символ).
Начало. Находимся в состоянии q0, ввели в машину данные: *111x11=*, головка машины располагается на первом символе *.
1-й шаг. Смотрим по таблице правил что будет делать машина, находясь в состоянии q0 и над символом «*». Это правило из 1-го столбца 5-й строки — q0*→q0*R. Это значит, что мы переходим в состояние q0 (то есть не меняем его), символ станет «*» (то есть не изменится) и смещаемся по введенному нами тексту «*111x11=*» вправо на одну позицию (R), то есть на 1-й символ 1. В свою очередь, состояние q01 (1-й столбец 1-я строка) обрабатывается правилом q01→q01R. То есть снова происходит просто переход вправо на 1 позицию. Так происходит, пока мы не станем на символ «х». И так далее: берем состояние (индекс при q), берем символ, на котором стоим (подчеркнутый символ), соединяем их и смотрим обработку полученной комбинации по таблице правил.
Простыми словами, алгоритм умножения следующий: помечаем 1-ю единицу 2-го множителя, заменяя ее на букву «а», и переносим весь 1-й множитель за знак равенства. Перенос производится путем поочередной замены единиц 1-го множителя на «а» и дописывания такого же количества единиц в конце строки (слева от крайнего правого «*»). Затем меняем все «а» до знака умножения «х» обратно на единицы. И цикл повторяется. Действительно, ведь A умножить на В можно представить как А+А+А В раз. Помечаем теперь 2-ю единицу 2-го множителя буквой «а» и снова переносим единицы. Когда до знака «=» не окажется единиц — значит умножение завершено.
Можно сказать, что машина Тьюринга представляет собой простейшую вычислительную машину с линейной памятью, которая согласно формальным правилам преобразует входные данные с помощью последовательности элементарных действий.
Элементарность действий заключается в том, что действие меняет лишь небольшой кусочек данных в памяти (в случае машины Тьюринга — лишь одну ячейку), и число возможных действий конечно. Несмотря на простоту машины Тьюринга, на ней можно вычислить все, что можно вычислить на любой другой машине, осуществляющей вычисления с помощью последовательности элементарных действий. Это свойство называется полнотой.
Один из естественных способов доказательства того, что алгоритмы вычисления, которые можно реализовать на одной машине, можно реализовать и на другой, — это имитация первой машины на второй.
Имитация заключается в следующем. На вход второй машине подается описание программы (правил работы) первой машины 
и входные данные 
, которые должны были поступить на вход первой машины. Нужно описать такую программу (правила работы второй машины), чтобы в результате вычислений на выходе оказалось то же самое, что вернула бы первая машина, если бы получила на вход данные .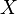
Как было сказано, на машине Тьюринга можно имитировать (с помощью задания правил перехода) все другие исполнители, за исключением конкурентных, каким-либо образом реализующие процесс пошагового вычисления, в котором каждый шаг вычисления достаточно элементарен.
На машине Тьюринга можно имитировать машину Поста, нормальные алгоритмы Маркова и любую программу для обычных компьютеров, преобразующую входные данные в выходные по какому-либо алгоритму. В свою очередь, на различных абстрактных исполнителях можно имитировать Машину Тьюринга. Исполнители, для которых это возможно, называются полными по Тьюрингу (Turing complete).
Есть программы для обычных компьютеров, имитирующие работу машины Тьюринга. Но следует отметить, что данная имитация неполная, так как в машине Тьюринга присутствует абстрактная бесконечная лента. Бесконечную ленту с данными невозможно в полной мере имитировать на компьютере с конечной памятью (суммарная память компьютера — оперативная память, жесткие диски, различные внешние носители данных, регистры и кэш процессора и др. — может быть очень большой, но, тем не менее, всегда конечна).
Сложение десятичных чисел
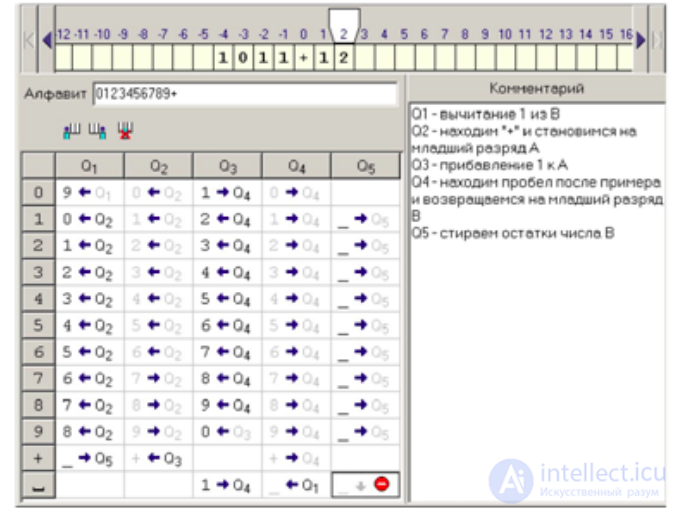
Вычитание десятичных чисел
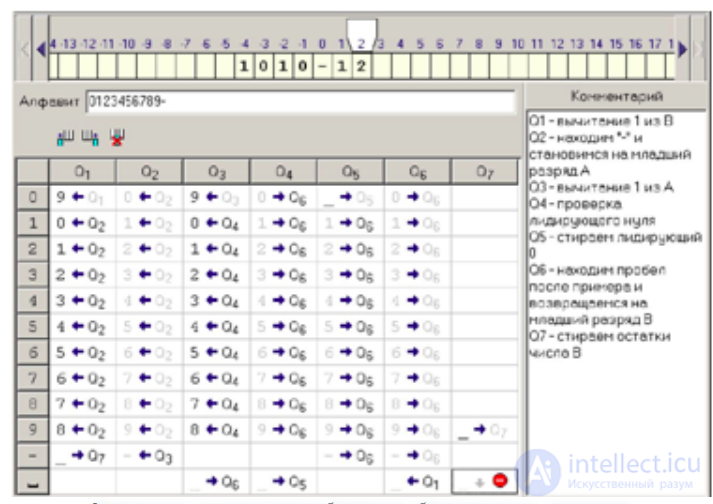
Модель машины Тьюринга допускает расширения. Можно рассматривать машины Тьюринга с произвольным числом лент и многомерными лентами с различными ограничениями. Однако все эти машины являются полными по Тьюрингу и моделируются обычной машиной Тьюринга.
В качестве примера такого сведения рассмотрим следующую теорему: Для любой машины Тьюринга существует эквивалентная машина Тьюринга, работающая на полубесконечной ленте.
Рассмотрим доказательство, приведенное Ю. Г. Карповым в книге «Теория автоматов». Доказательство этой теоремы конструктивное, то есть мы дадим алгоритм, по которому для любой машины Тьюринга может быть построена эквивалентная машина Тьюринга с объявленным свойством. Во-первых произвольно занумеруем ячейки рабочей ленты МТ, то есть определим новое расположение информации на ленте:
Затем перенумеруем ячейки, причем будем считать, что символ «*» не содержится в словаре МТ:
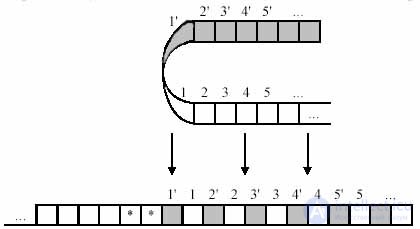
Наконец, изменим машину Тьюринга, удвоив число ее состояний, и изменим сдвиг головки считывания-записи так, чтобы в одной группе состояний работа машины была бы эквивалентна ее работе в заштрихованной зоне, а в другой группе состояний машина работала бы так, как исходная машина работает в незаштрихованной зоне. Если при работе МТ встретится символ ‘*’, значит головка считывания-записи достигла границы зоны:
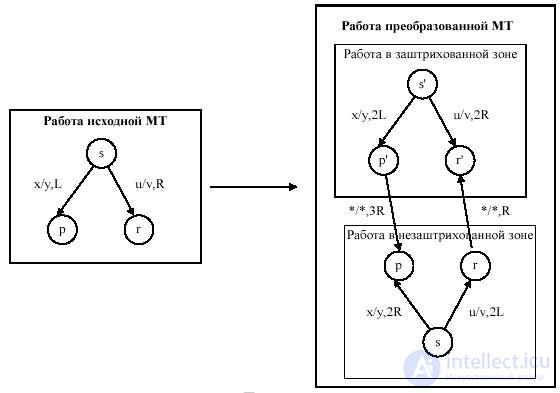
Начальное состояние новой машины Тьюринга устанавливается в одной или другой зоне в зависимости от того, в какой части исходной ленты располагалась головка считывания-записи в исходной конфигурации. Очевидно, что слева от ограничивающих маркеров «*» лента в эквивалентной машине Тьюринга не используется.
Тут, следует отметить, что термин "полубесконечность" едва ли имеет какой-либо внятный смысл, поскольку бесконечность деленная надвое также является бесконечностью, которая, в свою очередь, не имеет никаких "концов" по-определению. Тут, видимо, произошла терминологическая неточность из-за того, что в определении машины Тьюринга часто используется неформальное слово "бесконечная в обе стороны".
Недетерминированная машина Тьюринга — машина Тьюринга, функция перехода которой представляет собой недетерминированный конечный автомат.
Детерминированная (обычная, классическая) машина Тьюринга имеет функцию перехода, которая по комбинации текущего состояния и символа на ленте определяет три элемента: символ, который будет записан на ленте, направление смещения головки по ленте и новое состояние конечного автомата. Например, X на ленте в состоянии 3 однозначно определяет переход в состояние 4, запись на ленту символа Y и перемещение головки на одну позицию влево.
В случае недетерминированной машины Тьюринга, комбинация текущего состояния автомата и символа на ленте может допускать несколько переходов. Например, X на ленте и состоянии 3 допускает как состояние 4 с записью на ленту символа Y и смещением головки вправо, так и состояние 5 с записью на ленту символа Z и смещением головки влево.
В отличие от детерминированной машины Тьюринга, которая имеет единственный «путь вычислений», недетерминированный вариант имеет «дерево вычислений» (в общем случае — экспоненциальное число путей). Говорят, что недетерминированная машина Тьюринга допускает входные данные, если какая-нибудь ветвь этого дерева останавливается в допускающем состоянии, иначе НМТ входные данные не допускает. (Таким образом, ответы «да» и «нет» в случае недетерминированных вычислений несимметричны.)
Формально, недетерминированная машина Тьюринга — это шестерка объектов ,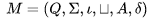 
где:
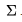— конечное множество символов (алфавит ленты)
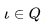— начальное состояние
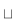— символ пробела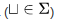 
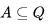— конечное множество допускающих состояний
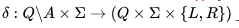— многозначное отображение из пары состояние-символ, называемое функцией перехода.Несмотря на кажущуюся большую мощность недетерминированных машин в связи с тем, что они выполняют несколько возможных вычислений сразу (требуя только, чтобы хоть одно из них заканчивалось в допускающем состоянии), любой язык, допускающийся недетерминированной машиной Тьюринга, также допускается и обычной детерминированной машиной Тьюринга, поскольку она может моделировать любой недетерминированный переход, делая многократные копии состояния, если встречается неоднозначность.
Моделирование недетерминизма требует значительно больше времени, вопрос об оценке разницы затрат открыт: в частном случае ограничения по времени в виде полинома от длины входа этот вопрос представляет собой классическую задачу «P = NP».
Класс алгоритмов, выполняемых за полиномиальное время на недетерминированных машинах Тьюринга, называется классом NP.
Рассмотрим задачу проверки того, что данное b-разрядное целое число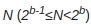 
является составным. Тогда b — длина входных данных, по отношению к которой рассматривается время вычисления. Ответ «ДА» — число составное и «НЕТ» — простое. Эта задача является комплементарной к тесту на простоту.
Недетерминированный алгоритм для этой задачи может быть, например, следующий:
(Алгоритм написан не непосредственно в виде определения машины Тьюринга.)
Во времени вычисления этого алгоритма определяющей частью является время выполнения деления, которое может быть выполнено за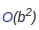 
шагов, что представляет собой полиномиальное время. Таким образом, задача находится в классе NP.
Для реализации такого времени вычисления требуется удачно выбирать число m или выполнять вычисления по всем возможным путям (для всех возможных m) одновременно на множестве копий машины.
Если моделировать этот алгоритм на детерминированной машине Тьюринга, пробуя по очереди все возможные варианты, требуется проверить N-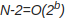 
ветвей. Таким образом, общее время вычислений будет 
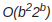шагов, что представляет собой уже экспоненциальное время, которое существенно больше, чем полиномиальное время. Таким образом, этот алгоритм не попадает в класс P. (Однако, могут быть применены другие, более быстрые алгоритмы для этой задачи, которые работают за полиномиальное время и, таким образом, задача попадает в класс P.)
Выводы из данной статьи про машина тьюринга детерминированная указывают на необходимость использования современных методов для оптимизации любых систем. Надеюсь, что теперь ты понял что такое машина тьюринга детерминированная, недетерминированная машина тьюринга, машина тьюринга и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов
Комментарии
Оставить комментарий
Теория цифровых автоматов
Термины: Теория цифровых автоматов