Это окончание невероятной информации про деревья решений.

...

соседа расширяется и на другие задачи, например, в рекомендательных системах простым начальным решением может быть рекомендация какого-то товара (или услуги), популярного среди ближайших соседей человека, которому хотим сделать рекомендацию;

На практике для больших выборок часто пользуются приближенными методами поиска ближайших соседей. Вот лекция Артема Бабенко про эффективные алгоритмы поиска ближайших соседей среди миллиардов объектов в пространствах высокой размерности (поиск по картинкам). Также известны открытые библиотеки, в которых реализованы такие алгоритмы, спасибо компании Spotify за ее библиотеку Annoy.

Качество классификации/регрессии методом ближайших соседей зависит от нескольких параметров:

• число соседей
• метрика расстояния между объектами (часто используются метрика Хэмминга, евклидово расстояние, косинусное расстояние и расстояние Минковского). Отметим, что при использовании большинства метрик значения признаков надо масштабировать. Условно говоря, чтобы признак "Зарплата" с диапазоном значений до 100 тысяч не вносил больший вклад в расстояние, чем "Возраст" со значениями до 100.
• веса соседей (соседи тестового примера могут входить с разными весами, например, чем дальше пример, тем с меньшим коэффициентом учитывается его "голос")

Класс KNeighborsClassifier в Scikit-learn

Основные параметры класса sklearn.neighbors.KNeighborsClassifier:

• weights: "uniform" (все веса равны), "distance" (вес обратно пропорционален расстоянию до тестового примера) или другая определенная пользователем функция
• algorithm (опционально): "brute", "ball_tree", "KD_tree", или "auto". В первом случае ближайшие соседи для каждого тестового примера считаются перебором обучающей выборки. Во втором и третьем — расстояние между примерами хранятся в дереве, что ускоряет нахождение ближайших соседей. В случае указания параметра "auto" подходящий способ нахождения соседей будет выбран автоматически на основе обучающей выборки.
• leaf_size (опционально): порог переключения на полный перебор в случае выбора BallTree или KDTree для нахождения соседей
• metric: "minkowski", "manhattan", "euclidean", "chebyshev" и другие

Выбор параметров модели и кросс-валидация

Главная задача обучаемых алгоритмов – их способность обобщаться, то есть хорошо работать на новых данных. Поскольку на новых данных мы сразу не можем проверить качество построенной модели (нам ведь надо для них сделать прогноз, то есть истинных значений целевого признака мы для них не знаем), то надо пожертвовать небольшой порцией данных, чтоб на ней проверить качество модели.

Чаще всего это делается одним из 2 способов:

• отложенная выборка (held-out/hold-out set). При таком подходе мы оставляем какую-то долю обучающей выборки (как правило от 20% до 40%), обучаем модель на остальных данных (60-80% исходной выборки) и считаем некоторую метрику качества модели (например, самое простое – долю правильных ответов в задаче классификации) на отложенной выборке.
• кросс-валидация (cross-validation, на русский еще переводят как скользящий или перекрестный контроль). Тут самый частый случай – K-fold кросс-валидация

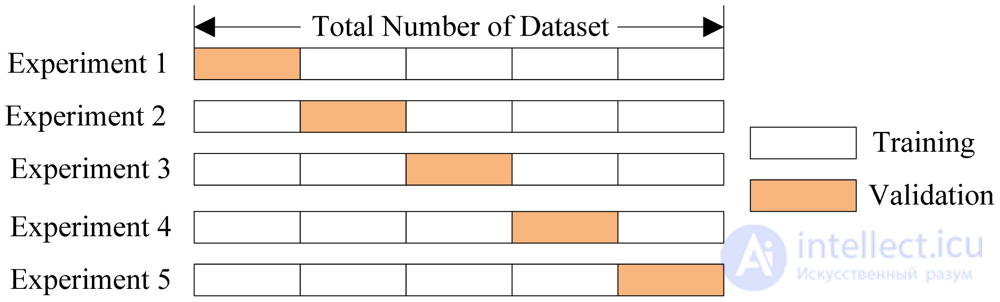
Тут модель обучается K раз на разных (K−1) подвыборках исходной выборки (белый цвет), а проверяется на одной подвыборке (каждый раз на разной, оранжевый цвет).
Получаются K оценок качества модели, которые обычно усредняются, выдавая среднюю оценку качества классификации/регрессии на кросс-валидации.

Кросс-валидация дает лучшую по сравнению с отложенной выборкой оценку качества модели на новых данных. Но кросс-валидация вычислительно дорогостоящая, если данных много.

Кросс-валидация – очень важная техника в машинном обучении (применяемая также в статистике и эконометрике), с ее помощью выбираются гиперпараметры моделей, сравниваются модели между собой, оценивается полезность новых признаков в задаче и т.д. Более подробно можно почитать, например, тут у Sebastian Raschka или в любом классическом учебнике по машинному (статистическому) обучению

Примеры применения

Деревья решений и метод ближайших соседей в задаче прогнозирования оттока клиентов телеком-оператора

Считаем данные в DataFrame и проведем предобработку. Штаты пока сохраним в отдельный объект Series, но удалим из датафрейма. Первую модель будем обучать без штатов, потом посмотрим, помогают ли они.

Считывание и предобработка данных

df = pd.read_csv('../../data/telecom_churn.csv')

df['International plan'] = pd.factorize(df['International plan']) 
df['Voice mail plan'] = pd.factorize(df['Voice mail plan']) 
df['Churn'] = df['Churn'].astype('int')
states = df['State']
y = df['Churn']
df.drop(['State', 'Churn'], axis=1, inplace=True)

Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели. Обучим 2 модели – дерево решений и kNN, пока не знаем, какие параметры хороши, поэтому наугад: глубину дерева берем 5, число ближайших соседей – 10.

Код

from sklearn.model_selection import train_test_split, StratifiedKFold
from sklearn.neighbors import KNeighborsClassifier

X_train, X_holdout, y_train, y_holdout = train_test_split(df.values, y, test_size=0.3,
random_state=17)

tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)

tree.fit(X_train, y_train)
knn.fit(X_train, y_train)

Качество прогнозов будем проверять с помощью простой метрики – доли правильных ответов. Сделаем прогнозы для отложенной выборки. Дерево решений справилось лучше: доля правильных ответов около 94% против 88% у kNN. Но это мы пока выбирали параметры наугад.

Код для оценки моделей

from sklearn.metrics import accuracy_score

tree_pred = tree.predict(X_holdout)
accuracy_score(y_holdout, tree_pred) # 0.94

knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred) # 0.88

Теперь настроим параметры дерева на кросс-валидации. Настраивать будем максимальную глубину и максимальное используемое на каждом разбиении число признаков. Суть того, как работает GridSearchCV: для каждой уникальной пары значений параметров max_depth и max_features будет проведена 5-кратная кросс-валидация и выберется лучшее сочетание параметров.

Настройка параметров моделей

from sklearn.model_selection import GridSearchCV, cross_val_score

tree_params = {'max_depth': range(1,11),
'max_features': range(4,19)}

tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)

tree_grid.fit(X_train, y_train)

Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:

tree_grid.best_params_

{'max_depth': 6, 'max_features': 17}

tree_grid.best_score_

0.94256322331761677

accuracy_score(y_holdout, tree_grid.predict(X_holdout))

0.94599999999999995

Теперь попробуем настроить число соседей в алгоритме kNN.

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

knn_pipe = Pipeline([('scaler', StandardScaler()), ('knn', KNeighborsClassifier(n_jobs=-1))])

knn_params = {'knn__n_neighbors': range(1, 10)}

knn_grid = GridSearchCV(knn_pipe, knn_params,
cv=5, n_jobs=-1,
verbose=True)

knn_grid.fit(X_train, y_train)

knn_grid.best_params_, knn_grid.best_score_

({'knn__n_neighbors': 7}, 0.88598371195885128)

accuracy_score(y_holdout, knn_grid.predict(X_holdout))

0.89000000000000001

В этом примере дерево показало себя лучше, чем метод ближайших соседей: 94.2% правильных ответов на кросс-валидации и 94.6% на отложенной выборке против 88.6% / 89% для kNN. Более того, в данной задаче дерево проявляет себя очень хорошо, и даже случайный лес (который пока представляем просто как кучу деревьев, которые вместе работают почему-то намного лучше, чем одно дерево) в этом примере показывает долю правильных ответов не намного выше (95.1% на кросс-валидации и 95.3% –на отложенной выборке), а обучается намного дольше.

Код для обучения и настройки случайного леса

from sklearn.ensemble import RandomForestClassifier

forest = RandomForestClassifier(n_estimators=100, n_jobs=-1, random_state=17)
print(np.mean(cross_val_score(forest, X_train, y_train, cv=5))) # 0.949

forest_params = {'max_depth': range(1,11),
'max_features': range(4,19)}

forest_grid = GridSearchCV(forest, forest_params,
cv=5, n_jobs=-1,
verbose=True)

forest_grid.fit(X_train, y_train)

forest_grid.best_params_, forest_grid.best_score_ # ({'max_depth': 9, 'max_features': 6}, 0.951)

accuracy_score(y_holdout, forest_grid.predict(X_holdout)) # 0.953

Нарисуем получившееся дерево. Из-за того, что оно не совсем игрушечное (максимальная глубина – 6), картинка получается уже не маленькой, но по дереву можно "прогуляться", если отдельно открыть рисунок.

Код для отрисовки дерева

export_graphviz(tree_grid.best_estimator_, feature_names=df.columns, 
out_file='../../img/churn_tree.dot', filled=True)
!dot -Tpng '../../img/churn_tree.dot' -o '../../img/churn_tree.png'

Сложный случай для деревьев решений

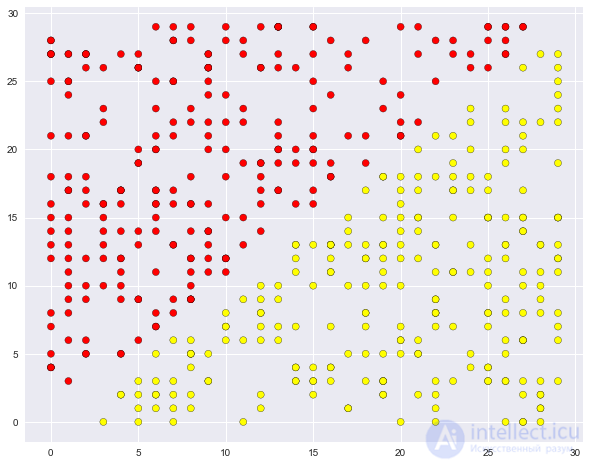
В продолжение обсуждения плюсов и минусов обсуждаемых методов приведем очень простой пример задачи классификации, с которым дерево справляется, но делает все как-то "сложнее", чем хотелось бы. Создадим множество точек на плоскости (2 признака), каждая точка будет относиться к одному из классов (+1, красные, или -1 – желтые). Если смотреть на это как на задачу классификации, то вроде все очень просто – классы разделяются прямой.

Код для генерации данных и картинки

def form_linearly_separable_data(n=500, x1_min=0, x1_max=30, x2_min=0, x2_max=30):
    data, target = [], []
    for i in range(n):
        x1, x2 = np.random.randint(x1_min, x1_max), np.random.randint(x2_min, x2_max)

        if np.abs(x1 - x2) > 0.5:
            data.append([x1, x2])
            target.append(np.sign(x1 - x2))
    return np.array(data), np.array(target)

X, y = form_linearly_separable_data()

plt.scatter(X[:, 0], X[:, 1], c=y, cmap='autumn', edgecolors='black');

Однако дерево решений строит уж больно сложную границу и само по себе оказывается глубоким. Кроме того, представьте, как плохо дерево будет обобщаться на пространство вне представленного квадрата 30×30, обрамляющего обучающую выборку.

Код для отрисовки разделяющей поверхности, которую строит дерево

tree = DecisionTreeClassifier(random_state=17).fit(X, y)

xx, yy = get_grid(X, eps=.05)
predicted = tree.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100, 
cmap='autumn', edgecolors='black', linewidth=1.5)
plt.title('Easy task. Decision tree compexifies everything');

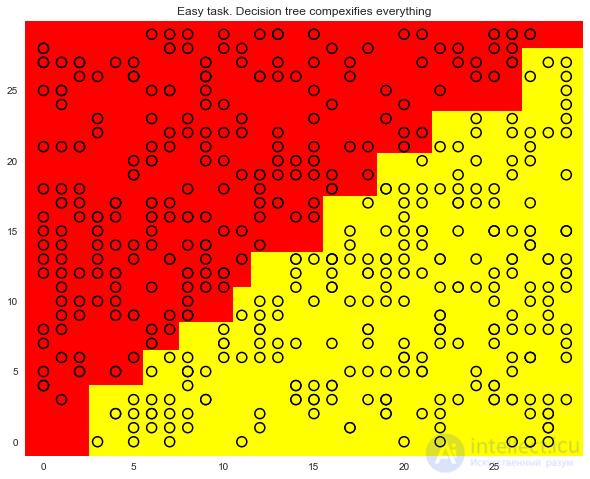
Вот такая сложная конструкция, хотя решение (хорошая разделяющая поверхность) – это всего лишь прямая x1=x2.

Код для отрисовки дерева

export_graphviz(tree, feature_names=['x1', 'x2'], 
out_file='../../img/deep_toy_tree.dot', filled=True)
!dot -Tpng '../../img/deep_toy_tree.dot' -o '../../img/deep_toy_tree.png'

Метод одного ближайшего соседа здесь справляется вроде лучше дерева, но все же не так хорошо, как линейный классификатор (наша следующая тема).

Код для отрисовки разделяющей поверхности, которую строит kNN

knn = KNeighborsClassifier(n_neighbors=1).fit(X, y)

xx, yy = get_grid(X, eps=.05)
predicted = knn.predict(np.c_[xx.ravel(), yy.ravel()]).reshape(xx.shape)
plt.pcolormesh(xx, yy, predicted, cmap='autumn')
plt.scatter(X[:, 0], X[:, 1], c=y, s=100, 
cmap='autumn', edgecolors='black', linewidth=1.5);
plt.title('Easy task, kNN. Not bad');

Деревья решений и метод ближайших соседей в задаче распознавания рукописных цифр MNIST

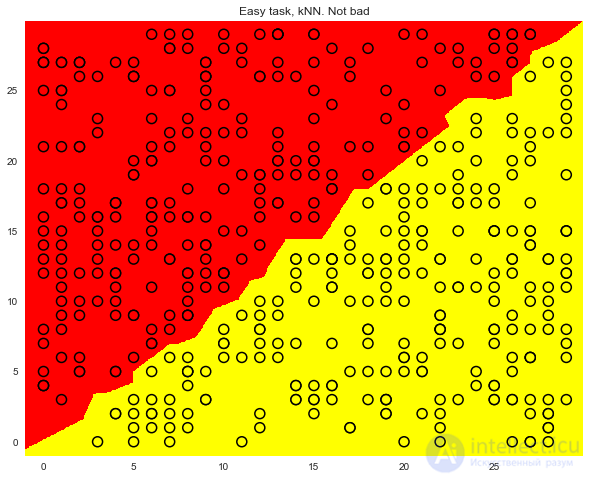
Теперь посмотрим на описанные 2 алгоритма в реальной задаче. Используем "встроенные" в sklearnданные по рукописным цифрам. Эта задача будет примером, когда метод ближайших соседей работает на удивление хорошо.

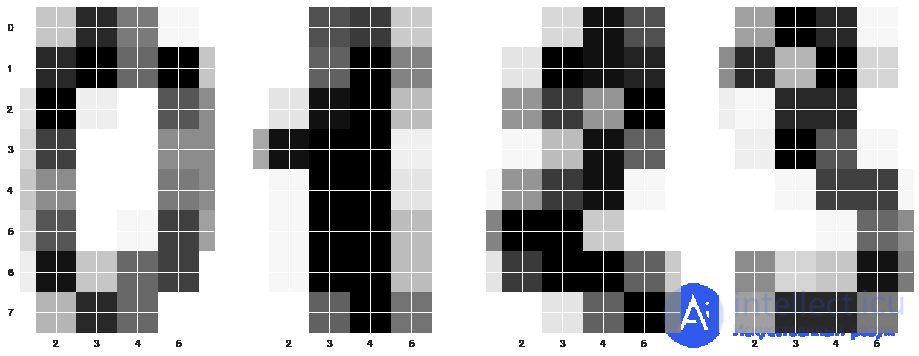
Картинки здесь представляются матрицей 8 x 8 (интенсивности белого цвета для каждого пикселя). Далее эта матрица "разворачивается" в вектор длины 64, получается признаковое описание объекта.

Нарисуем несколько рукописных цифр, видим, что они угадываются.

Загрузка данных и отрисовка нескольких цифр

from sklearn.datasets import load_digits

data = load_digits()
X, y = data.data, data.target

X[0,:].reshape([8,8])

array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])

f, axes = plt.subplots(1, 4, sharey=True, figsize=(16,6))
for i in range(4):
axes[i].imshow(X[i,:].reshape([8,8]));

Далее проведем ровно такой же эксперимент, как и в прошлой задаче, только диапазоны изменения настраиваемых параметров будут немного другие.

Настройка DT и kNN на данных MNIST

Выделим 70% выборки (X_train, y_train) под обучение и 30% будут отложенной выборкой (X_holdout, y_holdout). отложенная выборка никак не будет участвовать в настройке параметров моделей, на ней мы в конце, после этой настройки, оценим качество полученной модели.

X_train, X_holdout, y_train, y_holdout = train_test_split(X, y, test_size=0.3,
random_state=17)

Обучим дерево решений и kNN, опять параметры пока наугад берем.

tree = DecisionTreeClassifier(max_depth=5, random_state=17)
knn = KNeighborsClassifier(n_neighbors=10)

tree.fit(X_train, y_train)
knn.fit(X_train, y_train)

Сделаем прогнозы для отложенной выборки. Видим, что метод ближайших соседей справился намного лучше. Но это мы пока выбирали параметры наугад.

tree_pred = tree.predict(X_holdout)
knn_pred = knn.predict(X_holdout)
accuracy_score(y_holdout, knn_pred), accuracy_score(y_holdout, tree_pred) # (0.97, 0.666)

Теперь так же, как раньше настроим параметры моделей на кросс-валидации, только учтем, что признаков сейчас больше, чем в прошлой задаче — 64.

tree_params = {'max_depth': [1, 2, 3, 5, 10, 20, 25, 30, 40, 50, 64],
'max_features': [1, 2, 3, 5, 10, 20 ,30, 50, 64]}

tree_grid = GridSearchCV(tree, tree_params,
cv=5, n_jobs=-1,
verbose=True)

tree_grid.fit(X_train, y_train)

Лучшее сочетание параметров и соответствующая средняя доля правильных ответов на кросс-валидации:

tree_grid.best_params_, tree_grid.best_score_ # ({'max_depth': 20, 'max_features': 64}, 0.844)

Это уже не 66%, но и не 97%. Метод ближайших соседей на этом наборе данных работает лучше. В случае одного ближайшего соседа на кросс-валидации достигается почти 99% угадываний.

np.mean(cross_val_score(KNeighborsClassifier(n_neighbors=1), X_train, y_train, cv=5)) # 0.987

Обучим на этих же данных случайный лес, он на большинстве выборок работает лучше, чем метод ближайших соседей. Но сейчас у нас исключение.

np.mean(cross_val_score(RandomForestClassifier(random_state=17), X_train, y_train, cv=5)) # 0.935

Вы будете правы, если возразите, что мы тут не настраивали параметры RandomForestClassifier, но даже с настройкой доля правильных ответов не достигает 98%, как для у метода одного ближайшего соседа.

Результаты эксперимента
(Обозначения: CV и Holdout– средние доли правильных ответов модели на кросс-валидации и отложенной выборке соот-но. DT – дерево решений, kNN – метод ближайших соседей, RF – случайный лес)

	CV	Holdout
DT	0.844	0.838
kNN	0.987	0.983
RF	0.935	0.941

Вывод по этому эксперименту (и общий совет): вначале проверяйте на своих данных простые модели – дерево решений и метод ближайших соседей (а в следующий раз сюда добавится логистическая регрессия), может оказаться, что уже они работают достаточно хорошо.

Сложный случай для метода ближайших соседей

Теперь рассмотрим еще один простой пример. В задаче классификации один из признаков будет просто пропорционален вектору ответов, но методу ближайших соседей это не поможет.

Код для генерации шумных данных с паттерном

def form_noisy_data(n_obj=1000, n_feat=100, random_seed=17):
    np.seed = random_seed
    y = np.random.choice([-1, 1], size=n_obj)
    # первый признак пропорционален целевому
    x1 = 0.3 * y
    # остальные признаки – шум
    x_other = np.random.random(size=[n_obj, n_feat - 1])

    return np.hstack([x1.reshape([n_obj, 1]), x_other]), y

X, y = form_noisy_data()

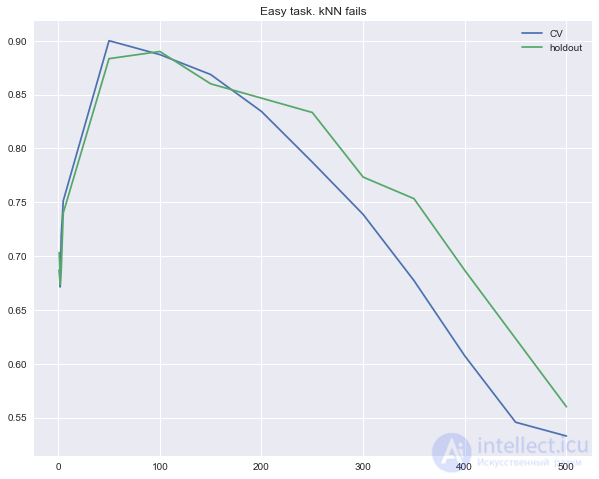
Как обычно, будем смотреть на долю правильных ответов на кросс-валидации и на отложенной выборке. Построим кривые, отражающие зависимость этих величин от параметра n_neighbors в методе ближайших соседей. Такие кривые называются кривыми валидации.

Видим, что метод ближайших соседей с евклидовой метрикой не справляется с задачей, даже если варьировать число ближайших соседей в широком диапазоне. Напротив, дерево решений легко "обнаруживает" скрытую зависимость в данных при любом ограничении на максимальную глубину.

Построение кривых валидации для kNN

from sklearn.model_selection import cross_val_score

cv_scores, holdout_scores = [], []
n_neighb = [1, 2, 3, 5] + list(range(50, 550, 50))

for k in n_neighb:

    knn = KNeighborsClassifier(n_neighbors=k)
    cv_scores.append(np.mean(cross_val_score(knn, X_train, y_train, cv=5)))
    knn.fit(X_train, y_train)
    holdout_scores.append(accuracy_score(y_holdout, knn.predict(X_holdout)))

plt.plot(n_neighb, cv_scores, label='CV')
plt.plot(n_neighb, holdout_scores, label='holdout')
plt.title('Easy task. kNN fails')
plt.legend();

Обучение дерева

tree = DecisionTreeClassifier(random_state=17, max_depth=1)
tree_cv_score = np.mean(cross_val_score(tree, X_train, y_train, cv=5))
tree.fit(X_train, y_train)
tree_holdout_score = accuracy_score(y_holdout, tree.predict(X_holdout))
print('Decision tree. CV: {}, holdout: {}'.format(tree_cv_score, tree_holdout_score))

Decision tree. CV: 1.0, holdout: 1.0

Итак, во втором примере дерево справилось с задачей идеально, а метод ближайших соседей испытал трудности. Впрочем, это минус скорее не метода, а используемой евклидовой метрики: в данном случае она не позволила выявить, что один признак намного лучше остальных.

Плюсы и минусы деревьев решений и метода ближайших соседей

Плюсы и минусы деревьев решений

Плюсы:

• Порождение четких правил классификации, понятных человеку, например, "если возраст < 25 и интерес к мотоциклам, то отказать в кредите". Это свойство называют интерпретируемостью модели;
• Деревья решений могут легко визуализироваться, то есть может "интерпретироваться" (строгого определения я не видел) как сама модель (дерево), так и прогноз для отдельного взятого тестового объекта (путь в дереве);
• Быстрые процессы обучения и прогнозирования;
• Малое число параметров модели;
• Поддержка и числовых, и категориальных признаков.

Минусы:

• У порождения четких правил классификации есть и другая сторона: деревья очень чувствительны к шумам во входных данных, вся модель может кардинально измениться, если немного изменится обучающая выборка (например, если убрать один из признаков или добавить несколько объектов), поэтому и правила классификации могут сильно изменяться, что ухудшает интерпретируемость модели;
• Разделяющая граница, построенная деревом решений, имеет свои ограничения (состоит из гиперплоскостей, перпендикулярных какой-то из координатной оси), и на практике дерево решений по качеству классификации уступает некоторым другим методам;
• Необходимость отсекать ветви дерева (pruning) или устанавливать минимальное число элементов в листьях дерева или максимальную глубину дерева для борьбы с переобучением. Впрочем, переобучение — проблема всех методов машинного обучения;
• Нестабильность. Небольшие изменения в данных могут существенно изменять построенное дерево решений. С этой проблемой борются с помощью ансамблей деревьев решений (рассмотрим далее);
• Проблема поиска оптимального дерева решений (минимального по размеру и способного без ошибок классифицировать выборку) NP-полна, поэтому на практике используются эвристики типа жадного поиска признака с максимальным приростом информации, которые не гарантируют нахождения глобально оптимального дерева;
• Сложно поддерживаются пропуски в данных. Friedman оценил, что на поддержку пропусков в данных ушло около 50% кода CART (классический алгоритм построения деревьев классификации и регрессии – Classification And Regression Trees, в sklearn реализована улучшенная версия именно этого алгоритма);
• Модель умеет только интерполировать, но не экстраполировать (это же верно и для леса и бустинга на деревьях). То есть дерево решений делает константный прогноз для объектов, находящихся в признаковом пространстве вне параллелепипеда, охватывающего все объекты обучающей выборки. В нашем примере с желтыми и синими шариками это значит, что модель дает одинаковый прогноз для всех шариков с координатой > 19 или < 0.

Плюсы и минусы метода ближайших соседей

Плюсы:

• Простая реализация;
• Неплохо изучен теоретически;
• Как правило, метод хорош для первого решения задачи, причем не только классификации или регрессии, но и, например, рекомендации;
• Можно адаптировать под нужную задачу выбором метрики или ядра (в двух словах: ядро может задавать операцию сходства для сложных объектов типа графов, а сам подход kNN остается тем же). Кстати, профессор ВМК МГУ и опытный участник соревнований по анализу данных Александр Дьяконов любит самый простой kNN, но с настроенной метрикой сходства объектов. Можно почитать про некоторые его решения (в частности, "VideoLectures.Net Recommender System Challenge") на персональном сайте;
• Неплохая интерпретация, можно объяснить, почему тестовый пример был классифицирован именно так. Хотя этот аргумент можно атаковать: если число соседей большое, то интерпретация ухудшается (условно: "мы не дали ему кредит, потому что он похож на 350 клиентов, из которых 70 – плохие, что на 12% больше, чем в среднем по выборке").

Минусы:

• Метод считается быстрым в сравнении, например, с композициями алгоритмов, но в реальных задачах, как правило, число соседей, используемых для классификации, будет большим (100-150), и в таком случае алгоритм будет работать не так быстро, как дерево решений;
• Если в наборе данных много признаков, то трудно подобрать подходящие веса и определить, какие признаки не важны для классификации/регрессии;
• Зависимость от выбранной метрики расстояния между примерами. Выбор по умолчанию евклидового расстояния чаще всего ничем не обоснован. Можно отыскать хорошее решение перебором параметров, но для большого набора данных это отнимает много времени;
• Нет теоретических оснований выбора определенного числа соседей — только перебор (впрочем, чаще всего это верно для всех гиперпараметров всех моделей). В случае малого числа соседей метод чувствителен к выбросам, то есть склонен переобучаться;
• Как правило, плохо работает, когда признаков много, из-за "прояклятия размерности". Про это хорошо рассказывает известный в ML-сообществе профессор Pedro Domingos – тут в популярной статье "A Few Useful Things to Know about Machine Learning", также "the curse of dimensionality" описывается в книге Deep Learning в главе "Machine Learning basics".

На этом мы подходим к концу, надеемся, этой статьи Вам хватит надолго. К тому же, есть еще и домашнее задание.

Задание

Актуальные домашние задания объявляются во время очередной сессии курса, следить можно в группе ВК и в репозитории курса.

В качестве закрепления материала предлагаем выполнить это задание – разобраться с тем, как работает дерево решений, на игрушечном примере, затем обучить и настроить деревья в задаче классификации данных Adult репозитория UCI. Проверить себя можно отправив ответы в веб-форме(там же найдете и решение).

Вау!! 😲 Ты еще не читал? Это зря!

• линейная регрессия ,
• Классификатор ближайшего центроида
• Проблема ближайшей пары точек
• теория принятия решений

Анализ данных, представленных в статье про деревья решений, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое деревья решений, метод ближайших соседей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Машинное обучение

Продолжение:

Часть 1 3. Классификация, деревья решений и метод ближайших соседей
Часть 2 Плюсы и минусы деревьев решений и метода ближайших соседей -