1. Подлинник ( противоположное или противоположность : копия, список).2. Текст, явившийся предметом перевода на другой язык.3. Рукопись или текст, предназначенные для полиграфического воспроизведения.4. То, что послужило предметом для живописного или фотографического изображения. 2. разговорное, Тот, кто отличается оригинальностью (2*), намеренно привлекая к себе внимание разного рода странностями.
1. То же, что подлинник. О. портрета, О. статьи (рукопись, с к-рой производится набор). 2. Непохожий на других, своеобразный человек, чудак ( разговорное ). Большой о.
1. Оригинала, (от латинское originalis - первоначальный). 1. Подлинник; противоположное или противоположность копия, список. Оригинал картины. Оригинал рукописи. Смели предпочесть оригиналы спискам. Грибоедов. Ѓ Рукопись или иной текст, с к-рого производится набор ( типографское дело ). Вычитать оригинал. Оригинал должен быть переписан на одной стороне листа. 2. Чудак, странный человек (разговорный). Оригинал! брюзглив, а без малейшей злобы! Грибоедов. Мало ли какие оригиналы бывают. А. Острвскй.
ОРИГИНАЛ
(лат. originalis - начальный, врожденный, от origo - происхождение). 1) в типографии: рукопись, с которой набирают и печатают. 2) подлинник, то есть картина, рисунок, статуя и проч., который делал сам мастер, воспроизводя природу или же свой идеал. 3) своеобразный человек, чудак. 4) рисунок, гравюра, с которого ученик срисовывает в классе.
ОРИГИНАЛ
1) первообраз, вещь, созданная самостоятельно; 2) в типографии - рукопись, с которой производится набор; 3) чудаковатый человек.
ОРИГИНАЛ
1) подлинник; вещь, созданная самостоятельно; рукопись, с которой делают набор в типографии; самостоятельное сочинение, а не перевод или компиляция, картина, статуя и т. падеж , в отличие от снятых с них копий; 2) своеобразный человек в хорошем и плохом смысле; чудак.
ОРИГИНАЛ
лат. originalis, начальный, врожденный, от origo, происхождение, рождение. а) Подлинник. b) Своеобычный человек. с) Рукопись, с которой набирают и печатают.
-а, м.
1.
То, что послужило предметом воспроизведения, копирования и т. падеж ; подлинник.
{Флор Федулыч:} Недавно купил {картину} на выставке-с. {Лавр Мироныч:} Оригинал? {Флор Федулыч:} Я копий не покупаю-с. А. Островский, Последняя жертва.
{Писец} читает оригинал доклада, копию которого --- проверяет высокий худой и длинный чиновник — Мухов. Серафимович, Преступление.
Красота статуи не может быть выше красоты живого индивидуального человека, потому что снимок не может быть прекраснее оригинала. Чернышевский, Эстетические отношения искусства к действительности.
Текст, послуживший предметом перевода на другой язык.
Близость перевода к оригиналу.
Ленин читал французского энциклопедиста {Дидро} в оригинале и сам переводил цитируемое место. Шагинян, Воспитание коммуниста.
Типогр.
Рукопись, с которой производится набор.
Вычитать оригинал.
— По каким оригиналам набирали вы прокламации у Рагозина? Федин, Первые радости.
2. Разг.
Странный, непохожий на других человек; чудак.
{Дергачев:} Ты скажи там всем, что я оригинал, --- что я могу хорошо одеваться, да не хочу. Мало ли какие оригиналы бывают! А. Островский, Последняя жертва.
Был с ним {Мысливечком} --- любопытнейший оригинал, художник и артист, ирландец Джемс Барри. Шагинян, Воскрешение из мертвых.
{От лат. originalis — первоначальный}
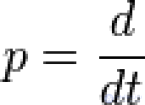... . t, что называется оригиналом , в функцию комплексной переменной p, что.называется изображением Свойства изображений Линейность Оригинал линейной комбинации функций равно линейной комбинации изображений с теми . же коэффициентами ... ... изображений с теми . же коэффициентами где a и b - произвольные комплексные числа Теорема подобия где a> Дифференцирование оригинала Дифференцирование изображения Интегрирование оригинала Интегрирование изображения Теорема смещения Теорема запаздывания ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
... F(p) и наоборот Приведены наиболее часто используемые свойства Свойство линейности При умножении оригинала на постоянную величину на ту же постоянную . величину умножается и изображение :. af (t) ≓ aF ... ... величину на ту же постоянную . величину умножается и изображение :. af (t) ≓ aF (p). Если оригинал представлен суммой функций , то изображение этой суммы равно . сумме изображений этих ... (Теоретические основы электротехники)
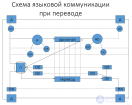... литературы , газетно-публицистический , официально-деловой , научно-технический ). Словарь терминов : •Источник (информации ) - автор текста оригинала , отправитель сообщения •Исходный язык (ИЯ ) - язык оригинала , язык с которого делается ... ... ряда мыслительных операций , выполняя которые , можно . осуществить процесс перевода всего оригинала или некоторой его части •Перевод - вид языкового посредничества , при котором содержание иноязычного текста ... (Теория перевода)
... модели и перехода от модели .к объекту (оригиналу ) В модельном эксперименте исследуется не объект («оригинал »;), а модель ; оригинал . непосредственно в самом эксперименте не участвует Некоторый объект становится ... ... отличаться от него Именно отличие и дает возможность «обойти »; препятствия , имеющиеся при изучении . оригинала Объективные основания модельного эксперимента заключаются в существовании общих закономерностей организации . и функционирования ... (Философия)
... после его выполнения Классическим примером устного перевода является такой перевод , когда переводчик воспринимает . оригинал в акустической форме («на слух »;) и в устной форме .произносит свой перевод При устном ... ... устном переводе создание текста перевода может происходить либо параллельно . восприятию оригинала , либо после того, как завершится восприятие оригинала Соответственно различаются два подвида устного перевода ... (Теория перевода)
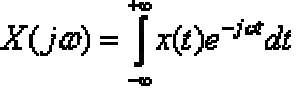... спектра Преобразование Фурье обратимо , то есть, зная Фурье-изображение , можно определить исходную . функцию – оригинал Соотношение обратного преобразования Фурье имеет следующий вид :. или в сокращенной записи , где - символ обратного ... ... . преобразования Лапласа Преобразование Лапласа обратимо , то есть, зная изображение по Лапласу , можно . определить оригинал , используя соотношение обратного преобразования или , где - символ обратного преобразования Лапласа Отметим , что преобразование ... (Математические основы теории автоматического управления)
Комментарии
Оставить комментарий