Привет, сегодня поговорим про бпф по основанию с прореживанием по частоте, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
бпф по основанию с прореживанием по частоте , настоятельно рекомендую прочитать все из категории Цифровая обработка сигналов.
Содержание
Введение
Алгоритм БПФ с прореживанием по частоте
Граф алгоритма с прореживанием по частоте
Сравнение алгоритмов БПФ по основанию 2 с прореживанием по времени и частоте
Выводы
Введение
Ранее был подробно рассмотрен алгоритм БПФ с прореживанием по времени. В данном параграфе рассмотрим еще один способ разбиения и объединения, который называется прореживание по частоте.
Алгоритм БПФ с прореживанием по частоте
Снова запишем выражение для дискретного преобразования Фурье сигнала


:
 |
(1) |
В алгоритме БПФ с прореживанием по времени производилось разделение исходного сигнала в соответствии с двоично-инверсной перестановкой. И получали первую и вторую половину спектра. В алгоритме с прореживанием по частоте наоборот исходный сигнал

делится пополам, т.е.

и


. Тогда выражение (1) можно переписать:
 |
(2) |
Учтем что
 |
(3) |
Тогда
 |
(4) |
Рассмотрим теперь четные отсчеты спектра

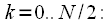
 |
(5) |
Учтем что
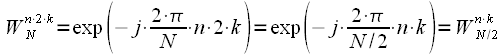 |
(6) |
Тогда
 |
(7) |
Таким образом четные отсчеты спектра рассчитываются как ДПФ суммы первой и второй половины исходного сигнала.
Рассмотрим теперь нечетные отсчеты спектра

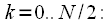
 |
(8) |
Окончательно выражение для четных и нечетных отсчетов спектра:
 |
(9) |
Прокомментируем полученный результат опираясь на все вышесказанное и с оглядкой на алгоритм с прореживанием по времени. Об этом говорит сайт https://intellect.icu . При делении сигнала на четные и нечетные отсчеты, в алгоритме с прореживанием по времени получали первую и вторую половины спектра. В данном случае алгоритм с прореживанием по частоте наоборот по первой и второй половине сигнала позволяет рассчитать четные и нечетные спектральные отсчеты (поэтому и называется прореживание по частоте). Разница алгоритмов еще и в том, что при прореживании по времени умножение на поворотные коэффициенты производилось после ДПФ четной и нечетной последовательности, а в данном алгоритме умножение на поворотные коэффициенты производится до ДПФ.
Граф алгоритма с прореживанием по частоте
Граф бабочка для алгоритма с прореживанием по частоте представлен на рисунке:
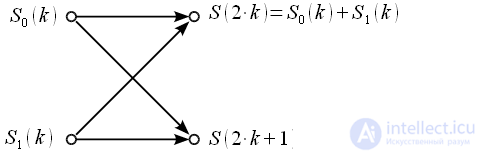
Рисунок 1: Граф бабочка для алгоритма БПФ с прореживанием по частоте
Поворотные коэффициенты в алгоритме с прореживанием по частоте полностью совпадают с поворотными коэффициентами алгоритма БПФ с прореживанием по времени.
Представим в виде графа алгоритм БПФ с прореживанием по частоте основанный на разбиении — объединении при

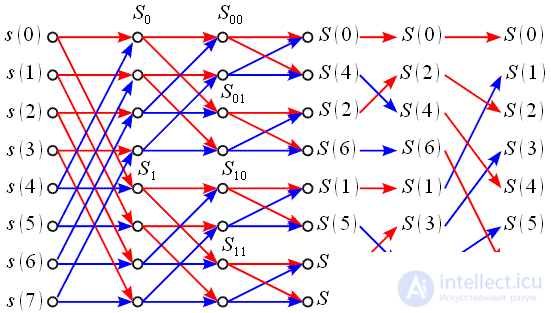
Рисунок 2: Граф алгоритма БПФ с прореживанием по частоте для N=8
На первом этапе исходный сигнал делится на 2 половины (красные и синие стрелочки). Далее вычисляются
 |
(10) |
Тогда если выполнить ДПФ
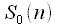
, то получим четные отсчеты спектра в соответствии с (9), а если ДПФ
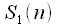
- то нечетные отсчеты спектра. Таким образом одно ДПФ длительности

заменили двумя ДПФ длительности

. Для вычисления каждой из ДПФ половинной длительности снова применим прореживание по частоте. В результате получим:
 |
(11) |
В результате получили 4 ДПФ по 2 точки каждое, которые также можно выполнить при помощи графа бабочки. На выходе получим спектральные отсчеты, которые будут переставлены. На первом уровне преобразования получались четные и нечетные отсчеты спектра, на втором уровне четные и нечетные отсчеты делились снова на четные и нечетные. В результате для расстановки спектральных отсчетов на места необходимо применить двоично-инверсную перестановку.
Сравнение алгоритмов БПФ по основанию 2 с прореживанием по времени и частоте
Таким образом можно сравнить алгоритм БПФ с прореживанием по частоте с алгоритмом БПФ с прореживанием по времени:
1. В обоих алгоритмах используется двоично-инверсная перестановка. В алгоритме с прореживанием по времени она используется вначале, в алгоритме с прореживанием по частоте — в конце.
2. В обоих алгоритмах используются одни и те же поворотные коэффициенты. В алгоритме с прореживанием по времени поворотные коэффициенты умножаются на результат укороченного ДПФ, а в алгоритме с прореживанием по частоте умножение на поворотные коэффициенты осуществляется до укороченного ДПФ.
3. В связи с вышесказанным, вычислительная эффективность обоих алгоритмов практически идентична.
Выводы
Подведем итог. В цикле из трех статьей были рассмотрены пути уменьшения вычислительных затрат при использовании ДПФ. Рассмотрены наиболее распространенные алгоритмы БПФ с прореживанием по времени и по частоте и показана эффективность данных алгоритмов.
Необходимо отметить, что алгоритмы БПФ не ограничиваются алгоритмом с прореживанием по времени и по частоте. Существует множество других алгоритмов, например алгоритмы по основанию четыре, обобщенные алгоритмы для произвольных длин и т.д. Существует также алгоритм Винограда, обеспечивающий минимальное количество умножений из всех возможных алгоритмов. Но на практике наиболее широко используются именно алгоритмы по основанию два. Это обусловлено несколькими причинами:
1. Простота программной реализации алгоритмов и в тоже время высокая эффективность.
2. Выигрыши получаемые альтернативными алгоритмами БПФ незначительные по сравнению с алгоритмами по основанию два и нивелируются экспоненциально растущими вычислительными мощностями процессоров.
3. Алгоритмы по основанию два прекрасно «распараллеливаются» при использовании жесткой логики.
Все это переводит альтернативные алгоритмы БПФ в разряд «экзотики», и на практике как правило алгоритмы по основанию два являются оптимальным выбором. Однако если возникнет необходимость всегда можно обратится к литературе.
Нам осталось ответить на последний вопрос: есть ли у алгоритмов БПФ недостатки? Оказывается есть. В результате того что ускорение вычислений достигается за счет максимального использования данных рассчитанных на предыдущем этапе, в алгоритме БПФ происходит когерентное накопление ошибок округления при умножении и сложении. Однако данный эффект оказывает сколь-нибудь существенное влияние при арифметике с фиксированной точкой и представлении чисел с количеством разрядов менее 8-ми. При представлении чисел с плавающей точкой или 8-ми или большей разрядности данным эффектом можно пренебречь, так как он практически не повлияет на точность расчета спектра.
Надеюсь, эта статья про бпф по основанию с прореживанием по частоте, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое бпф по основанию с прореживанием по частоте
и для чего все это нужно, а если не понял, или есть замечания,
то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Цифровая обработка сигналов
Из статьи мы узнали кратко, но содержательно про бпф по основанию с прореживанием по частоте

 :
:
 делится пополам, т.е.
делится пополам, т.е.  и
и 
 . Тогда выражение (1) можно переписать:
. Тогда выражение (1) можно переписать:



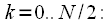

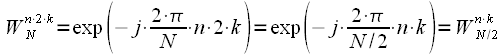


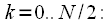






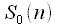 , то получим четные отсчеты спектра в соответствии с (9), а если ДПФ
, то получим четные отсчеты спектра в соответствии с (9), а если ДПФ 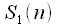 - то нечетные отсчеты спектра. Таким образом одно ДПФ длительности
- то нечетные отсчеты спектра. Таким образом одно ДПФ длительности  заменили двумя ДПФ длительности
заменили двумя ДПФ длительности . Для вычисления каждой из ДПФ половинной длительности снова применим прореживание по частоте. В результате получим:
. Для вычисления каждой из ДПФ половинной длительности снова применим прореживание по частоте. В результате получим:
Комментарии
Оставить комментарий
Цифровая обработка сигналов
Термины: Цифровая обработка сигналов