1.4.Параметрическая идентификация

Привет, Вы узнаете о том , что такое 1.4.Параметрическая идентификация, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1.4.Параметрическая идентификация , настоятельно рекомендую прочитать все из категории Идентификация систем управления.

1.4.1.Схемы реализации параметрической идентификации

Методы оценивания параметров моделей объектов в общем случае можно разделить на два класса в зависимости от способа реализации процедуры оценивания. К первому типу относятся подходы на основе использования явных математических выражений, ко второму – реализации процедур оценивания с использованием настраиваемой модели.

При реализации методов оценивания первого типа (рис. 1.6) математическая модель задается в виде явных математических соотношений, содержащих набор подлежащих определению числовых A .

На объекте проводятся идентификационные эксперименты по сбору массивов входных U (t) и выходных Y (t) данных. Далее осуществляется обработка результатов. На основе полученных экспериментальных данных строится модель, обеспечивающая минимальное значение функционала J (Y, Ym , Am ) . Оптимальные процедуры оценива-

ния параметров A в этом случае сводятся к разрешению следующего уравнения:

дJ

= 0.

(1.13)

дA

m

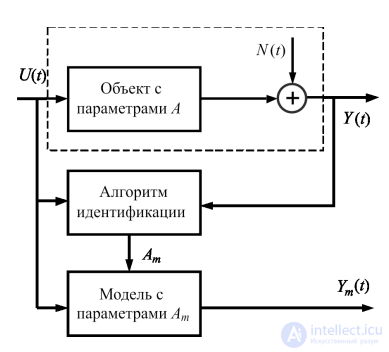
Рис. 1.6. Явная схема реализации алгоритма идентификации

Оценивание параметров в этом случае осуществляется при помощи ретроспективных алгоритмов идентификации, когда решение получается в результате обработки всего массива данных путем выполнения конечного числа элементарных операций и не может быть получено как результат промежуточных вычислений. Такая процедура оценивания, с инженерной точки зрения, относится к методам идентификации вне контура регулирования и не позволяет обрабатывать поступающие наблюдения последовательно, в режиме нормальной эксплуатации.

Структурная схема реализации процедуры оценивания на основе настраиваемой модели [12–14] приведена на рис. 1.7.

При реализации методов оценивания второго типа (см. рис. 1.7) используется принцип подстройки модели к объекту по признакам близости поведения. В этом случае модель объекта исследования, представленная параметрами Am , изменяется таким образом, чтобы

характеристики модели были близки к характеристикам исследуемой системы. Оптимальные процедуры оценивания параметров Am в этом случае сводятся к разрешению следующего уравнения:

дJ → 0. (1.14)

дAm

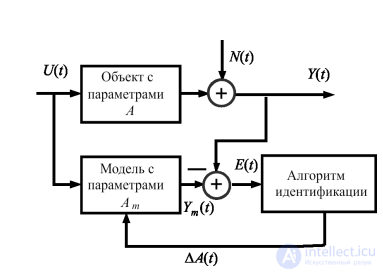
Рис. 1.7. Схема реализации алгоритма идентификации с настраиваемой моделью

Невязка E(t) поступает на вход блока алгоритма идентификации, который изменяет параметры настраиваемой модели Am на основе

решения уравнения (1.14). Решение получается, в принципе, как результат бесконечного числа таких операций, при этом каждый промежуточный результат представляет приближенное решение.

Этот тип реализации относится к методам идентификации в замкнутом контуре и позволяет проводить оперативную идентификацию в режиме нормального функционирования объекта.

Следует отметить [15–17], что с появлением цифровых вычислительных устройств стало удобнее реализовывать используемые функции (вычисление критерия, автоматическая настройка, др.) алгоритмически, что приводит к стиранию четких границ между различными способами идентификации. Основным признаком, указывающим на применение методов идентификации с настраиваемой моделью, следует считать наличие обратной связи.

Среди возможных алгоритмов идентификации широкое распространение получили рекуррентный метод наименьших квадратов (МНК), а также метод стохастической аппроксимации (МСА). Методу наименьших квадратов соответствует минимизация квадратичного критерия (1,10). МСА характеризуется простотой и универсальностью и позволяет не ограничиваться квадратичными критериями идентификации, а формировать разнообразные как линейные, так и нелинейные алгоритмы идентификации .

Особенности каждой из схемы реализации алгоритма идентификации приведены в табл. 1.1.

Таблица 1.1

1.4.2. Классификация моделей объектов управления

Существует большое разнообразие типов и классов моделей. Ни один из способов классификации не дает полную картину и не отражает всех свойств используемых моделей, так как характеризует только отдельные признаки модели.

Рассмотрим основные типы моделей, разделяющиеся по основным системным признакам [6, 9].

1. Физические (натурные) и математические (символьные). Физическими являются модели, в которых свойства реального

объекта представляются характеристиками вещественного объекта той же или аналогичной природы.

К математическим моделям относятся те, в которых для описания характеристик объекта используются математические конструкции. В дальнейшем будем рассматривать только математические модели.

2. Одномерные и многомерныe.

Одномерными называют объекты, имеющие один вход и один выход, многомерные (многосвязные) объекты имеют несколько входов и несколько выходов.

3. Статические или динамические.

Объект называется динамическим, если его выходное воздействие зависит не только от входного воздействия в текущий момент времени, но и от предыдущих значений входа. Это означает, что объект обладает инерционностью (памятью). Математические модели динамических объектов задают его поведение во времени.

Объект называется статическим, если его реакция на входное воздействие не зависит от предыстории, от поведения системы в прошлом, а также от предыдущих значений входа. Статические системы обладают мгновенной реакцией на входное воздействие, модели описывают процессы, не изменяющиеся во времени, т.е. поведение объекта в установившихся режимах.

4. Линейные или нелинейные.

Объект называется линейным, если для него справедлив принцип суперпозиции, т.е. реакция объекта на линейную комбинацию (суперпозицию) двух входных воздействий равна той же самой комбинации реакций данного объекта на каждое из воздействий:

f (α1u1(t) +α2u2 (t)) = α1 f (u1(t)) +α2 f (u2 (t)) ,

(1.15)

где u1(t), u2 (t) – входные воздействия; α1, α2 – произвольные коэф-

фициенты.

В противном случае объект считается нелинейным. 5. Стационарные или нестационарные.

Объект называется стационарным, если его реакция на одинаковые входные воздействия не зависит от времени приложения этих воздействий, т.е. параметры такого объекта не зависят от времени.

Впротивном случае говорят, что объект нестационарный.

6.Дискретные или непрерывные.

Объект называется непрерывным, если состояние его входных и выходных воздействий изменяется или измеряется непрерывно в течение определенного промежутка времени.

Объект называется дискретным, если состояние его выходов и входов определено лишь в дискретные моменты времени. Для опи-

25

сания дискретных систем используются решетчатые функции, являющиеся аналогами непрерывных функций, и разностные уравнения, являющиеся аналогами дифференциальных уравнений.

7. Детерминированные или стохастические.

Объект называется детерминированным, если его выходное воздействие однозначно определяется структурой объекта и входными воздействиями и не зависит от неконтролируемых случайных факторов. В реальных условиях наблюдаемые выходные сигналы изменяются не только под воздействием наблюдаемых входов, но и из-за многочисленных ненаблюдаемых случайных помех. Если эти помехи малы или отсутствуют, то систему можно считать детерминированной.

Система, в которой случайные помехи оказывают существенное влияние на выходные переменные, называется стохастической. Стохастическая (вероятностная) модель отражает воздействие случайных факторов, поэтому между входными и выходными переменными существует не однозначная функциональная зависимость, а вероятностная. Обычно переменные состояния стохастического объекта оцениваются в терминах математического ожидания, а входные воздействия – вероятностными законами распределения.

8. Сосредоточенные и распределенные.

Объект называется объектом с сосредоточенными параметрами, если его входные и выходные величины зависят только от времени (только от одной переменной). Модели объектов с сосредоточенными параметрами содержат одну или несколько производных по времени от переменных состояния и представляют собой обыкновенные дифференциальные уравнения. Математическая модель переходных процессов в объекте наряду с дифференциальным уравнением содержит также дополнительные условия однозначности – начальныеусловия.

Объект называется объектом с распределенными параметрами, если выходная величина зависит от нескольких переменных – от времени и от пространственных координат. Такая ситуация обычно имеет место, когда исследуемая характеристика объекта, например, температура, концентрация вещества и другие, распределена в некотором объеме. В этом случае математическая модель объекта содержит частные производные и описывает как динамику процесса во времени, так и распределенность характеристики в пространстве. Математическая модель процессов в распределенном объекте включает диффе-

26

ренциальное уравнение в частных производных, начальные условия и граничные условия. Примером такой модели может служить волновое уравнение, модель диффузии или теплопроводности:

дQ(x, t)

= a

д2Q(x, t)

+ f (x, t, u(x, t)),

(1.16)

дt

дx2

где Q(x, t) – функция состояния одномерного объекта с распределен-

ными параметрами x [x0 , x1], a, f – заданные коэффициент и функ-

ция соответственно.

9. Характеристики «вход–выход» и описание в пространстве состояния.

Характеристиками типа «вход–выход» являются определенные операторы, связывающие поведение выходной величины объекта со входной, например, передаточная, переходная, весовая функции.

Модели пространства состояний описывают динамическое поведение системы с n координатами, называемыми координатами состояния. Такими координатами, например, являются значения функции и ее n −1 производные в произвольный момент времени. Они составляют n-мерный вектор, полностью определяющий состояние системы в любой момент времени в n-мерном пространстве состояний или фазовом пространстве.

Координаты вектора состояния, в отличие от векторов входных и выходных величин, в общем случае являются абстрактными математическими характеристиками, физическая природа которых несущественна. Координаты вектора состояния, а также структура и значения коэффициентов уравнений состояний зависят от выбора базиса

вфазовом пространстве.

10.Структурированные и агрегированные.

Структурированная модель является представлением математической модели всей системы в целом как совокупности относительно более простых моделей отдельных элементов и блоков объекта, соединенных между собой посредством связей. Она характеризует как физические, так и технические аспекты построения системы управления и позволяет исследовать процессы, происходящие как во всей системе в целом, так и в отдельных ее элементах. Таким образом, структурированная модель системы управления представляет совокуп-

ность ряда взаимосвязанных математических моделей отдельных звеньев. В такой модели, последовательно исключая из рассмотрения все внутренние переменные, являющиеся входными или выходными сигналами внутренних звеньев, можно найти дифференциальное уравнение, описывающее взаимосвязь входной и выходной величин системы и являющееся по сути агрегированной моделью.

Агрегированная модель описывает функциональные взаимосвязи между входными и выходными величинами без учета внутренней структуры и взаимосвязей в системе.

11. Параметрические и непараметрические.

Параметрические модели описываются заданными в явной форме аналитическими зависимостями, содержащими параметры, подлежащие идентификации. Эти зависимости представляют собой параметрические модели конечной размерности, например, дифференциальные уравнения определенного порядка, модели в пространстве состояний. Параметрами являются численные значения величин, определяющих выход модели (например, значения коэффициентов обыкновенных дифференциальных уравнений, начальных условий, коэффициентов передаточных функций). Методами параметрической идентификации определяются неизвестные коэффициенты уравнения объекта илипередаточной функции.

Непараметрические модели сводятся к описанию преобразований сигналов пространства входов в элементы пространства выходов. В этом случае модель объекта определяется оператором преобразования функций входных сигналов в функции выходных величин. Непараметрическими моделями являются весовые функции, передаточные функции (если заранее не задано число коэффициентов), корреляционные функции, спектральные плотности, ряды Вольтерра. Например, для модели в виде весовой функции связь между входными и выходными сигналами для линейных объектов задается с помощью интеграла свертки (интеграла Дюамеля):

∞∞

y(t) = ∫w(t)u(t −τ)dτ = ∫u(t)w(t −τ)dτ,

(1.17)

0

0

где w(t) – импульсная переходная (весовая) функция объекта, являющаяся непараметрической модельюлинейного динамического объекта.

Методы непараметрической идентификации используются для определения временных или частотных характеристик объектов. По полученным характеристикам далее можно определить передаточную функцию или уравнения объекта. Параметрические модели могут при-

28

водить к большим ошибкам, если порядок модели не соответствует порядку объекта. Преимущество непараметрических моделей состоит

втом, что они не требуют явного знания порядка объекта. Однако

вэтом случае описание является, по существу, бесконечномерным.

1.4.3. Математическое описание основных классов моделей

Основные классы моделей имеют следующее математическое описание.

1. Статические модели.

Статическая характеристика объекта – это зависимость между входными и выходными сигналами в установившемся режиме. Аналитически в общем случае уравнение модели статического объекта имеет вид нелинейной функции многих переменных:

y = f (u).

(1.18)

Во многих практических случаях общую нелинейную функцию (1.18) удается параметризовать некоторым вектором A , тогда эта зависимость принимает вид

y = f (u, A)

(1.19)

и задача идентификации сводится к определению неизвестных параметров A .

Частным случаем параметрических моделей [3, 13] являются модели, линейные относительно оцениваемых параметров:

y = a0 +a1u1 +K+ anun.

(1.20)

Моделью статического линейного многомерного объекта с n входами и m выходами является система линейных алгебраических уравнений:

y = a + a u + a u

2

+K+ a

u

n

,

1

10

11 1

12

1n

y2 = a20 + a21u1 +a22u2 +K+ a2nun ,

(1.21)

M

y

m

= a

m0

+ a

u + a

m2

u

2

+K+ a u

n

,

m1

1

mn

где aij – неизвестные параметры модели, подлежащие определению.

В векторно-матричной форме система (1.21) имеет вид

Y = A0 + AU ,

(1.22)

29

где U и Y – векторы входных и выходных воздействий; A0 и A – со-

ответственно вектор и матрица коэффициентов модели, подлежащие идентификации.

Математическое описание (1.20) называется одномерной линейной регрессией, (1.21)–(1.22) – многомерной линейной регрессией. На практике большинство задач можно свести к линейной регрессии, поэтому идентификация параметров линейной регрессии является важной задачей и будет рассмотрена ниже.

2. Линейные динамические непрерывные параметрические модели. Линейные динамические непрерывные модели в теории управле-

ния могут быть заданы в следующих формах:

• Обыкновенные дифференциальные уравнения n-го порядка:

a

d n y(t)

+ a

d n−1 y(t)

+K+ a

n

y(t) =

dtn

dtn−1

0

1

(1.23)

d m x(t)

d m−1x(t)

= b

+b

+K+b x(t),

dtm

dtm−1

0

1

m

где ai ,bj (i =1,n, j =1,m) – параметры модели, подлежащие идентифи-

кации. Для большинства реальных физически реализуемых систем управления m ≤ n.

• Передаточные функции.

Если к дифференциальному уравнению (1.23) задать нулевые начальные условия, то, применяя преобразование Лапласа, получают передаточную функцию линейного объекта в следующем виде:

y( p)

b pm +b pm−1

+K+b

W ( p) =

=

0

1

m

,

(1.24)

x( p)

a pn + a pn−1

+K+ a

0

1

n

где p – комплексная переменная – параметр преобразования Лапласа.

• Уравнения в пространстве состояний.

Динамические процессы, наряду с дифференциальным уравнением n-го порядка (1.24), также можно описать системой n обыкновенных дифференциальных уравнений первого порядка:

dyi (t)

n

m

= ∑aij y j +∑biju j , i =

.

(1.25)

1,n

dt

j=1

j=1

Вводя в описание вектор состояний системы, представим модель в пространстве состояний в следующей матричной форме:

dX (t) = AX (t) + BU (t),

(1.26)

dt

Y (t) = CX (t) + DU (t),

где X (t) – вектор внутренних (динамических) переменных;

U (t) –

вектор входных переменных; Y (t) – вектор выходных переменных; A – матрица коэффициентов системы; B – матрица входа системы; C – матрица выхода системы; D – матрица обхода системы.

С учетом воздействия внешней среды, при наличии входной адди-

тивной помехи N(t) и погрешностей измерения ε(t)

базовая форму-

лировка модели имеет вид

dX (t) = AX (t) + BU (t) + KN(t),

(1.27)

dt

Y (t) = CX (t) + DU (t) +ε(t),

где помимо рассмотренных ранее обозначений также присутствуют N(t) – вектор случайных воздействий – помех; ε(t) – вектор шумов измерения; K – матрица, описывающая канал прохождения помехи.

Воздействия N(t) и ε(t) , как правило, полагаются гауссовскими случайными процессами в виде белого шума.

Рассмотренная модель (1.27) может быть представлена структурной схемой в пространстве состояний (рис. Об этом говорит сайт https://intellect.icu . 1.8).

Рис. 1.8. Структурная схема линейной динамической системы в пространстве состояния при учете воздействий внешней среды

31

3. Линейные динамические дискретные параметрические модели. Линейные динамические дискретные модели могут принимать

следующий вид [2, 6, 17]:

• Обыкновенные разностные уравнения.

Универсальной характеристикой для дискретных моделей является разностное уравнение n-го порядка, где используется понятие разности как аналога понятию производной для непрерывных моделей:

an y(k) +an−1 y(k −1) +K+ a0 y(k −n) =

(1.28)

= bmu(k) +bm−1u(k −

1) +K+b0u(k −m),

где y(k), u(k) – значения выходной и входной величин в k-й момент времени.

• Дискретные передаточные функции.

Применяя оператор сдвига во времени z, задаваемый соотношением y(k +i) = zi y(k) к конечно-разностному уравнению (1.28), получаем операторную форму дискретной модели:

y(z)

b +b

z−1

+K+b z−m

W (z) =

=

m

m−1

0

.

(1.29)

x(z)

a

+K+ a z−n

+ a

n−1

z−1

n

n

• Уравнения в пространстве состояний.

Используя для описания

динамики дискретного

объекта дис-

кретные переменные состояния, образующие n-мерный вектор состоя-

x (k)

1

ния

X (k) =

x2

(k)

получают описание объекта в пространстве со-

M

,

xn

(k)

стояний в следующей векторно-матричной форме:

X (k +1) = AX (k) + BU (k),

(1.30)

Y (k) = CX (k) + DU (k).

Структурное представление модели (1.30) приведено на рис. 1.9.

32

U (k)

X (k +1)

X (k)

Y (k)

B

z−1

C

A

D

Рис. 1.9. Структурная схема дискретной модели

впространстве состояния

4.Нелинейные динамические модели.

Класс нелинейных динамических систем по сравнению с линейными системами значительно шире, так как в этих системах протекают многообразные явления и процессы, не характерные для линейных систем. Вследствие этого для описания таких систем становится неприменим математический аппарат теории линейных систем, поэтому при решении задачи получения математических моделей нелинейных систем используются следующие два основных подхода [15, 18]. Один подход заключается в получении приближенного математического описания линеаризованной модели (по сути в определении эквивалентной исходной нелинейной модели) с помощью методов линеаризации: гармонической, статистической или методом малых приращений. Наиболее применим такой подход для объектов, имеющих гладкие характеристики, и процессов, протекающих при небольших отклонениях и возмущениях относительно номинальных режимов функционирования.

При втором подходе математическая модель рассматривается как существенно нелинейная. В этом случае наиболее распространенными видами моделей являются следующие:

• Нелинейные дифференциальные уравнения.

Для непрерывного одномерного объекта управления связь между входным и выходным сигналами записывается в общем виде неявным выражением

dy

, K,

d n y

, u,

du

, K,

d mu

= 0,

(1.31)

F y,

dtn

dt

dt

dtm

33

где F – некоторый нелинейный оператор, который требуется идентифицировать. Если возможно, то проводится параметризация нелинейной модели (1.31) на основе структурирования F с введением некоторого вектора параметров A:

F y, dy

, K,

d n y, u, du, K,

d mu, A

= 0.

(1.32)

dt

dtn

dt

dtm

В этом случае задача идентификации сводится к определению оператора F и к оцениванию его вектора параметров A .

Для нелинейного дискретного объекта строятся аналогичные нелинейные разностные уравнения.

• Модели Гаммерштейна.

Такие модели нелинейных инерционных объектов строятся в предположении, что нелинейность и инерционность объекта можно разделить, его можно представить в виде последовательной комбинации двух звеньев: нелинейного безынерционного и динамического линейного. Модели «вход–выход» для таких объектов в одномерном стационарном случае могут иметь два варианта описания:

∞

y(t) = ∫w(τ)F(u(t −τ))dτ

(1.33)

0

или

∞

(1.34)

y(t) = F ∫w(τ)u(t −τ)dτ ,

0

где w(τ) – импульсная переходная функция линейного звена;

F(u) –

статическая характеристика нелинейного звена.

Структурное представление моделей объекта для каждого из вариантов описания приведено на рис. 1.10–1.11.

Рис. 1.10. Структурная схема модели Гаммерштейна (1.33)

34

Рис. 1.11. Структурная схема модели Гаммерштейна (1.34)

• Разложение Вольтерра.

При данном способе описания зависимость между входом u(t)

и выходом y(t)

представляется рядом [1, 3]

t

t t

y(t) = ∫w1

(τ)u(t −τ)dτ+ ∫∫w2

(τ1,τ2 )u(t −τ1)u(t −τ2 )dτ1τ2 +... , (1.35)

0

0 0

где w1(τ), w2 (τ1,τ2 ), w3 (τ1,τ2 ,τ3 )K – обобщенные весовые функции (яд-

ра) i-го порядка. Такой ряд (1.35) носит название ряда Вольтерра. Разложение в ряд Вольтерра является непосредственным обобще-

нием линейной модели в форме интеграла свертки на нелинейные объекты. Задача идентификации при этом состоит в определении обобщенных весовых функций w1(τ), w2 (τ1,τ2 ), w3 (τ1,τ2 ,τ3 )K. Для не-

стационарного объекта ядра будут зависеть от t .

• Описание в пространстве состояний.

В общем случае уравнения состояния для конечномерных непрерывных систем записываются в следующем виде:

dx(t)

= f (x(t), u(t), t),

dt

y(t) = g(x(t), u(t), t),

(1.36)

x(t0 ) = x0.

В общем случае в уравнениях (1.36) определению подлежат нелинейные функции f и g. При возможности их параметризации некоторым вектором параметров A описание системы принимает вид

dx(t)

= f (x(t), u(t), A, t),

dt

y(t) = g(x(t), u(t), A, t),

(1.37)

x(t0 ) = x0.

35

Уравнения пространства состояний для дискретных нелинейных объектов при параметризации нелинейных функций A имеют вид

x(k +1) = f (x(k), u(k), A),

y(k) = g(x(k), u(k), A),

(1.38)

x(k0 ) = x0.

Представление в пространстве состояний особенно удобно для многомерных объектов. Для нестационарных объектов необходимо ввести зависимость вектора A от времени.

1.4.4. Управляемость, наблюдаемость и идентифицируемость систем

Важными понятиями для исследования систем, в том числе и для идентификации, являются понятия управляемости, наблюдаемости и идентифицируемости систем [3, 7, 8].

Рассмотрим каждое из этих понятий подробнее.

Система является управляемой, если она может быть переведена из любого начального состояния X (t0 ) в любое другое желаемое со-

стояние X (tk ) за конечный интервал времени τ(τ = tk −t0 ) путем задания (изменения) входного воздействия U (t) .

Понятие управляемости можно проиллюстрировать следующим примером (рис. 1.12).

Рис. 1.12. Структурная схема неуправляемой системы

Очевидно, что эта система является неуправляемой, так как управляющее воздействие u(t) влияет не на все переменные состоя-

ния (переменная состояния x4 (t) не поддается управлению).

36

Система является наблюдаемой, если все переменные состояния могут быть непосредственно или косвенно определены по выходному вектору системы.

Если управляемость системы требует, чтобы каждое состояние системы было чувствительно к входному воздействию, то наблюдаемость требует, чтобы каждое состояние системы влияло на измеряемый выходной вектор.

Следует различать понятия «измеряемость» и «наблюдаемость». Измерить переменную непосредственно с помощью измерительных устройств означает непосредственно с помощью измерительных средств зафиксировать значение переменной в текущий момент времени. Наблюдаемая переменная – это либо измеренная, либо вычисленная на основе измеренных переменных переменная.

Понятие наблюдаемости можно проиллюстрировать следующим примером (рис. 1.13).

Рис. 1.13. Структурная схема неуправляемой системы

Очевидно, что эта система является ненаблюдаемой, так как не все переменные состояния X (t) могут быть восстановлены на основе выходного измеренного вектора Y (t) (ИЭ – измерительный элемент). Так, динамическая переменная x5 (t) является ненаблюдаемой.

Система автоматического управления (САУ) является идентифицируемой, если по вектору переменных состояний можно определить параметры модели.

Управляемость, наблюдаемость и идентифицируемость системы определяют по следующим критериям.

37

Пусть описание САУ представлено в терминах пространства состояния

dX (t)

= AX (t) + BU (t)

,

(1.39)

dt

Y (t) = CX (t) + DU (t)

где X (t) – вектор внутренних (динамических) переменных;

U (t) –

вектор входных переменных; Y (t) – вектор выходных переменных; A – матрица коэффициентов системы; B – матрица входа системы; C – матрица выхода системы; D – матрица обхода системы.

Система будет управляемой только в том случае, если матрица управляемости имеет ранг n, где n – порядок системы (т.е. порядок вектора состояния X (t) ):

M y =[BM ABM A2 BMKAn−1B], (1.40) rank(M y ) = n.

Система будет наблюдаемой только в том случае, если матрица наблюдаемости имеет ранг n, где n – порядок системы (т.е. порядок вектора состояния X (t) )

T

T T

T 2

T

T

n−1

C

T

Mн = C

M A C

M (A )

C

MK(A )

,

(1.41)

rank(Mн) = n.

Система будет идентифицируемой в том случае, если матрица идентифицируемости имеет ранг n, где n – порядок системы (т.е. порядок вектора состояния X (t) ).

Mи = V (0)M AV (0)M (A)2V (0)MK(A)n−1V (0) , (1.42) rank(Mи) = n.

1.4.5. Идентификация линейной регрессионной модели

Наиболее распространенным методом оценивания параметров, служащим базовым подходом к параметрической идентификации, является метод наименьших квадратов, который в предположении линейности и дискретности во времени объекта приводит к наиболее простым и универсальным решениям. Задача состоит в следующем: по

38

имеющимся выборочным данным наблюдений за входным и выходным сигналами требуется оценить значения параметров, обеспечивающих минимум величины функционала невязки между модельными и фактическими данными:

J = ET IE → min.

(1.43)

Функция невязки

E =Y −Ym

(1.44)

представляет собой разность между выходом исследуемого объекта Y и реакцией, вычисленной по математической модели объекта Ym. Не-

вязка складывается из неточностей структуры модели, погрешностей измерений и неучтенных взаимодействий среды и объекта. Однако, независимо от происхождения возникающих ошибок, МНК минимизирует сумму квадратичной невязки значений.

В принципе, МНК не требует никакой априорной информации о помехе. Но для того чтобы полученные оценки обладали желательными свойствами, будем предполагать, что помеха является случайным процессом типа белого шума.

Важным свойством оценок по МНК является существование только одного локального минимума, совпадающего с глобальным. Поэтому оценка Am является единственной. Ее значение определяется

из условия экстремума функционала (1.43):

дJ = 0. (1.45)

дAm

Оценивание линейной системы по методу наименьших квадратов называется линейным регрессионным анализом благодаря линейному оператору модели.

Обратимся к основам линейного регрессионного анализа для оценивания параметров одномерных и многомерных линейных статических систем [7, 14, 19].

Рассмотрим линейную статическую систему, представленную на рис. 1.14, имеющую n входов U и один выход y .

Эта система может быть описана следующим линейным уравнением:

y = a0 +a1u1 +K+ anun.

(1.46)

39

Рис. 1.14. Схема одномерной системы

u1

Используя серию измерений величин U = u2 и y в течение оп-

Mun

ределенного отрезка времени t [t0 , tk ], можно сформировать матрицу измерений величин U и Y следующим образом:

u (1)

u

(1)

L

u

n

(1)

U =

1

2

,

u1(2)

u2 (2)

L

un (2)

M

(k) u2 (k) L

u1

un (k)

y(1)

Y =

y(2)

,

M

y(k)

где ui ( j) – значение i-й входной переменной,

измеренной в момент

времени t j = t0 + j∆t; ∆t

– интервал дискретизации, ∆t =

tk −t0

.

продолжение следует...

Продолжение:

Часть 1 1.4.Параметрическая идентификация
Часть 2 - 1.4.Параметрическая идентификация