1.3. Структурная идентификация

структурная идентификация , идентификация в широком смысле, идентификация типа «черный ящик», имеет место при отсутствии априорной информации об объекте: не известны структура объекта, класс объекта, размерность и т.д. Главная задача структурной идентификации – определение структуры модели [3, 8, 10]. В рамках структурной идентификации необходимо выделить значимые переменные состояния, выбрать общую структуру и тип модели, класс уравнений, которыми предполагается описывать наблюдаемый процесс; выделить значимые. Для успешного решения задачи структурной идентификации требуется использовать априорные сведения о физических, химических или иных явлениях, происходящих в процессе, знание формальных аналитических свойств моделей, инженерные навыки и интуицию. До настоящего времени общих формальных подходов к решению задачи структурной идентификации не существует, и этап структурной идентификации часто сводится к эвристическому заданию структуры модели на основе априорных сведений об объекте.

Выработаны общие рекомендации по решению задач структурной идентификации [11]:

1. Выделение объекта из внешней среды.

Этап выделения объекта определяется целями и алгоритмом управления. Однако нельзя сформулировать цель без предварительной модели объекта управления, поэтому еще до формулировки цели некоторая модель должна быть выбрана. Как правило, модель в первом приближении – это модель, построенная на основе физических, химических, механических и других законов управления. Процесс выделения объекта из среды – последовательный переход от простых моделей объекта к более сложным моделям путем «наращивания модели» за счет определенных элементов среды, которые изначально не учитывались в модели, но оказывают существенное влияние на функционирование объекта.

Такую громоздкую процедуру вряд ли можно формализовать, поэтому на данном этапе структурной идентификации широко используется метод экспертного опроса, по результатам которого и принимается решение о структуре объекта, его взаимодействии со средой, возможных состояниях среды и т.д.

2. Ранжирование входов и выходов объекта по степени их влияния на выполнение целей управления в объекте.

Этап ранжирования входов и выходов объекта выявляет всевозможных претендентов на роль входов и выходов, выделяя из них наиболее существенные. Отбор входов должен соответствовать следующим требованиям:

• • входные переменные U =[u1, u1,K, un ] должны быть контролируемыми;
• • отбираются только те входные переменные U =[u1, u1,K, un ], состояние которых влияет на реализацию целей в объекте.

Ранжирование входных переменных осуществляется по рангуKi . Вход, влияющий наибольшим образом на реализацию целей в объекте, имеет ранг Ki =1. Входы располагаются в порядке возрастания ран-

гов. Ранжирование на основе рангов входных переменных может осуществляться методами экспертной оценки, непосредственного ранжирования, методом парных сравнений [11].

3. Определение рационального числа входов и выходов объекта, учитываемых в модели.

Определение рационального числа входных и выходных переменных также осуществляется на основе экспертных оценок. Выбор начинается с минимального количества входов и выходов, и путем наращивания выбирается оптимальное количество входных и выходных переменных.

4. Определение типа (класса) моделей.

При выборе класса модели необходимо руководствоваться следующими рекомендациями .

Тип модели задается в виде:

F = (L, N, M , D), (1.5)

где L, N, M , D – булевые переменные, т.е. переменные, принимающие значение либо 0 (нет), либо 1 (да) и определяющие основные свойства модели: L – линейность; N – непрерывность; M – многомерность; D – детерминированность. Обычно идентификация начинается с расчета самой простой модели, а именно объект представляется в виде линейной, непрерывной, одномерной и детерминированной модели

F = (1,1, 0,1).

Начинать построение необходимо с физической модели (по известным законам физики, не забывая о цели построения модели).

Следует постараться преобразовать модель к виду линейной рег-

рессии:

yi = a0 +a1 u1 +...+an un. (1.6)

5. Выбор критерия согласия .

Модель объекта всегда неточна. Неточность модели по отноше-

нию к объекту определяется функцией невязки

ei = ym − yi , (1.7)

i

где ym – значение i-й выходной переменной модели;

yi – значение i-й i выходной переменной объекта.

Таким образом, критерием оптимальности (или критерием согласия) в задачах идентификации является функция невязки.

Выбор наилучшей функции проводится по минимуму этого критерия.

Минимизацию критерия можно осуществить следующими методами:

• Метод наименьших квадратов.

Оценивание по методу наименьших квадратов не требует никакой априорной информации об объекте.

Критерий идентификации имеет вид

J = ET IE → min , (1.8)

e1

где E – ошибка системы, E = e2 ; I – единичная матрица.

Men

• Марковские оценки (или обобщенный метод наименьших квадратов).

Для применения марковских оценок должна быть известна ковариационная матрица аддитивного шума:

ξ[n(1)n(1)]L ξ[n(1)n(k)] ,(1.9)

N =MKM K

ξ[n(k)n(1)]

ξ[n(k)n(k)]

где ξ[n(i)n( j)] – корреляционная функция аддитивного шума для моментов времени i, j .

Ковариационная матрица должна быть известна априорно, исходя из характеристик шумовых помех, действующих на объект управления

(рис. 1.5).

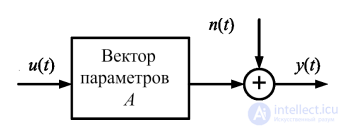
Рис. 1.5. Схема объекта для задачи идентификации

Критерий идентификации имеет вид

J = ET N −1E → min. (1.10)

• Метод максимального правдоподобия.

Метод максимального правдоподобия априорно кроме шумовых характеристик требует знания о влиянии переменных друг на друга, представленные в виде корреляционных матриц.

Априорно известно, что выборочные значения выходных переменных Y являются случайными величинами с совместным распределением вероятностей p( y(1),L, y(k), A).

Апостериори (после измерений) становятся известными реализации этих случайных величин: y(1) = c1, ..., y(k) = ck . По ним определя-

ется вектор параметров A . Функциональная связь между c1, ..., ck и A называется функцией правдоподобия и определяется совместным рас-

пределением вероятностей (многомерный случай)

L = p(c1, ..., ck , A). (1.11)

Функция правдоподобия является функцией оцениваемых параметров модели A .

Критерий идентификации имеет вид

L{c1, ..., ck , A} → max. (1.12)

Примеры подходов к структурной идентификации:

1. Методы информационных критериев:

   • Для выбора структуры модели используются критерии, такие как критерий Акаике (AIC) и критерий Байеса (BIC). Эти критерии позволяют находить компромисс между точностью описания данных и сложностью модели, чтобы избежать переобучения.

2. Методы обратной задачи:

   • Для некоторых систем можно решать обратные задачи, когда данные о поведении системы используются для восстановления ее структуры. Например, в биологических системах или экономике такие подходы могут помочь в выявлении закономерностей.

3. Эвристические и нейросетевые методы:

   • В сложных случаях, когда структура системы неизвестна или слишком сложна для аналитического описания, применяются методы на основе нейронных сетей, генетических алгоритмов и других эвристических подходов для поиска оптимальной структуры модели.

4. Построение моделей на основе физических законов:

   • В инженерных и физических системах структурная идентификация может начинаться с использования физических законов (например, уравнений движения или законов сохранения) для определения общей формы модели, а затем проводится уточнение этой модели на основе данных.

Применение структурной идентификации:

Структурная идентификация необходима в случаях, когда:

• Система сложная и ее физические законы неизвестны или недостаточно описаны.
• Модель должна быть гибкой, чтобы включать новые переменные или параметры по мере поступления данных.
• Данные содержат значительное количество шума, что затрудняет выбор модели без специальных методов.

Примеры включают задачи в биоинформатике, экономике, энергетике и управлении сложными техническими объектами.