Лекция
Привет, Вы узнаете о том , что такое математические нотации, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое математические нотации, префиксная, инфиксная, постфиксная, обратная польская запись, польская нотация , настоятельно рекомендую прочитать все из категории Информатика.
Нотации Распространенные нотации
1. инфиксная нотация
2. польская нотация ( префиксная нотация) запись
3. обратная польская запись (нотация) ( постфиксная нотация)
4 Перевод из инфиксной нотации в постфиксную. Обратная польская запись
Нота́ция (от лат. notatio «записывание; замечание»)- система условных обозначений, принятая в какой-либо области знаний или деятельности. Включает множество символов, используемых для представления понятий и их взаимоотношений, составляющее алфавит нотации, а также правила их применения.
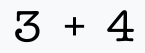
Инфиксная нотация — это форма записи математических и логических формул, в которой операторы записаны в инфиксном стиле между операндами, на которые они воздействуют (например, 2 + 2). Задача разбора выражений, записанных в такой форме, для компьютера сложнее по сравнению с префиксной (то есть + 2 2) или постфиксной (2 2 +). Однако эта запись используется в большинстве языков программирования как более естественная для человека.
В инфиксной нотации, в отличие от префиксной и постфиксной, скобки, окружающие группы операндов и операторов, определяют порядок, в котором будут выполнены операции. При отсутствии скобок операции выполняются согласно правилам приоритета операторов.
Инфиксная запись может отличаться от функциональной, где имя функции описывает какую-то операцию, а ее аргументы являются операндами. Примером функциональной записи может быть S(1,3) в которой функция S означает операцию сложения: S(1,3) = 1+3 = 4.
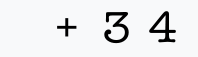
Не следует путать с Обратной польской нотацией.
Польская нотация (запись), также известна как префиксная нотация (запись), это форма записи логических, арифметических и алгебраических выражений. Характерная черта такой записи — оператор располагается слева от операндов. Если оператор имеет фиксированную арность, то в такой записи будут отсутствовать круглые скобки и она может быть интерпретирована без неоднозначности. Польский логик Ян Лукасевич изобрел эту запись примерно в 1920, чтобы упростить пропозициональную логику.
Алонзо Черч упоминал эту нотацию в своей классической книге по математической логике, как достойную внимания систему нотации и даже противопоставлял экспозиции логических нотаций Альфреда Уайтхеда и Бертрана Рассела в Principia Mathematica.[1]
Несмотря на то, что польская запись не используется в математике, она широко применяется в информатике.
В префиксной нотации сложение чисел 1 и 2 будет записано «+ 1 2» вместо записи «1 + 2». В более сложных выражениях операторы предшествуют операндам, но операнды сами могут быть нетривиальными выражениями, содержащими свои собственные операторы. Например, выражение, которое в традиционной инфиксной нотации записывается
(5 − 6) * 7
в префиксной может быть записано как
*(− 5 6) 7
или просто
* − 5 6 7
Так как любая простая арифметическая операция является бинарной, то ее префиксное представление не может быть интерпретировано двояко, поэтому нет необходимости использовать скобки. В предыдущем примере в традиционной, инфиксной записи круглые скобки были необходимы, а теперь переместим их
5 − (6 * 7)
или просто удалим
5 − 6 * 7
это изменит смысл и результат вычисления всего выражения. Соответствующая префиксная запись такого выражения будет выглядеть следующим образом:
− 5 * 6 7
Вычисление вычитания задерживается до тех пор пока не будут считаны оба операнда (5 и результат перемножения 6 и 7). Как и в любой другой нотации, выражения находящиеся в глубине вычисляются первыми, но в польской записи глубина выражения определяется порядком, а не скобками.
Префиксная запись в простой арифметике представляет в значительной степени академический интерес. Как и постфиксная запись, префиксная нотация была использована для некоторых коммерческих вычислительных машин (HP-11С). Изучение префиксной записи часто является первым шагом в области конструирования компиляторов.
Префиксная запись широко применяется в s-выражениях в языке программирования Лисп, где скобки необходимы, поскольку арифметические операторы обладают различной арностью. Язык программирования Ambi использует польскую запись для арифметических операций и структуры программы. Постфиксная запись используется во многих стековых языках, таких как PostScript, и является основой для многих вычислительных машин (калькуляторов), особенно для вычислительных машин Hewlett-Packard.
Также важно отметить, что количество операндов в выражении должно быть на один больше чем количество операций, иначе выражение не имеет смысла (учитывая, что в выражении используются только бинарные операции). Этому можно легко не придавать значения при работе с длинными, сложными выражениями, что повлечет за собой ошибки. Поэтому необходимо обращать внимание на количество операций и операндов при использовании префиксной нотации.
Порядок операций определяется структурой префиксной нотации и может быть легко определен. Главное, нужно помнить, что при вычислении выражения порядок операндов нужно сохранять. Это не важно для операций, которые обладают свойством коммутативности, но для некоммутативных операций, таких как вычитание и деление, этот факт является ключевым для анализа выражения. Например, следующее выражение:
/ 10 5 = 2 (префиксная запись)
нужно прочесть, как «деление 10 на 5». Поэтому результатом вычисления будет 2, а не ½, что было бы результатом неправильного анализа выражения.
Префиксная запись особенно популярна в стековых языках благодаря свойственной им возможности легко различать порядок операций без использования скобок. Для выявления порядка вычисления операторов в префиксной нотации даже нет необходимости запоминать всю операционную иерархию, как при инфиксной нотации. Вместо того, чтобы анализировать выражение для обнаружения оператора, который нужно вычислить первым, нужно считывать выражение слева направо, рассматривая оператор и ближайшие к нему два операнда. Если среди этих операндов находится еще один оператор, то вычисление первого оператора откладывается, до тех пор, пока не будет вычислен новый оператор. Итерации этого процесса повторяются до тех пор, пока оператор не будет вычислен, что должно в конечном счете произойти, если в выражении количество операндов на один больше, чем количество операций (в случае бинарных операций). Как только оператор вычислен, он и его два операнда заменяются полученным значением (операндом). Поскольку оператор и два операнда заменяются на вычисленный операнд, то становится на один оператор и один операнд меньше. После этого в выражении также остается N операторов и N+1 операнд, что позволяет итеративно продолжать процесс.
В приведенном ниже примере можно увидеть, что сложное на первый взгляд выражение в префиксной нотации, на самом деле оказывается не таким уж сложным для понимания (справа от знака равенства соответствующее выражение в инфиксной записи):
- * / 15 - 7 + 1 1 3 + 2 + 1 1 = 15 / (7 - (1 + 1)) * 3 - (2 + (1 + 1))
- * / 15 - 7 2 3 + 2 + 1 1 = 15 / (7 - 2) * 3 - (2 + (1 + 1))
- * / 15 5 3 + 2 + 1 1 = 15 / 5 * 3 - (2 + (1 + 1))
- * 3 3 + 2 + 1 1 = 3 * 3 - (2 + (1 + 1))
- 9 + 2 + 1 1 = 9 - (2 + (1 + 1))
- 9 + 2 2 = 9 - (2 + 2)
- 9 4 = 9 - 4
5 = 5
Таблица, приведенная ниже, демонстрирует ядро записи предложенной Яном Лукасевичем для пропозициональной логики. Некоторые буквы Польской записи означают конкретные слова на польском языке:

Заметим, что в работе Лукасевича о многозначной логике кванторы упорядочены по пропозициональной ценности.

Не следует путать с (прямой) польской нотацией.
Обра́тная по́льская запись (англ. Reverse Polish notation, RPN) — форма записи математических и логических выражений, в которой операнды расположены перед знаками операций. Также именуется как обратная польская запись, обратная бесскобочная запись, постфиксная нотация, бесскобочная символика Лукасевича, польская инверсная запись, ПОЛИЗ.
Стековой машиной называется алгоритм, проводящий вычисления по обратной польской записи (см. ниже пример вычисления выражений).
Обратная польская нотация (ОПН) была разработана австралийским философом и специалистом в области теории вычислительных машин Чарльзом Хэмблином в середине 1950-х на основе польской нотации, которая была предложена в 1920 году польским математиком Яном Лукасевичем. Работа Хэмблина была представлена на конференции в июне 1957, и издана в 1957 и 1962.
Первыми компьютерами, поддерживающими обратную польскую нотацию, были KDF9 от English Electric Company, который был анонсирован в 1960 и выпущен (появился в продаже) в 1963, и американский Burroughs B5000, анонсирован в 1961, выпущен в том же 1963. Один из проектировщиков B5000, Р. С. Бартон, позже написал, что разработал обратную польскую запись независимо от Хэмблина, примерно в 1958, в процессе чтения книги по символьной логике, и до того как познакомился с работой Хэмблина.
Компания Friden перенесла ОПН в настольные калькуляторы, выпустив в июне 1964 модель EC-130. А в 1968 инженеры Hewlett-Packard разработали настольный калькулятор 9100A с поддержкой ОПН. Этот калькулятор сделал обратную польскую нотацию популярной среди ученых и инженеров, даже несмотря на то, что в ранней рекламе 9100A ОПН не упоминалась. В 1972 калькулятор HP-35 с поддержкой ОПН стал первым научным карманным калькулятором.
В 1971 году появился оригинальный язык программирования Forth, языковая машина которого имеет двухстековую структуру и где все вычисления проводятся на стеке. В этом языке ОПН является естественным способом записи любых операций с данными, хотя возможна, при желании, реализация и обычной (инфиксной) записи арифметических операций.
ОПН применялась в советском инженерном калькуляторе Б3-19М (совместная разработка с ГДР), выпущенном в 1976 году. Все выпускаемые в СССР вплоть до конца 1980-х годов программируемые микрокалькуляторы, за исключением «Электроника МК-85» и «Электроника МК-90», использовали ОПН — она проще реализовывалась и позволяла обойтись в программировании вычислений меньшим числом команд, по сравнению с обычной алгебраической нотацией, а количество программной памяти в этих моделях всегда было критическим ресурсом. ОПН используется в современных российских программируемых калькуляторах «Электроника МК-152» и «Электроника МК-161», что обеспечивает их совместимость с программами, написанными для советских калькуляторов.

Отличительной особенностью обратной польской нотации является то, что все аргументы (или операнды) расположены перед знаком операции. В общем виде запись выглядит следующим образом:
Например, рассмотрим вычисление выражения 7 2 3 * − (эквивалентное выражение в инфиксной нотации: 7 − 2 * 3).
Очевидное расширение обратной польской записи на унарные, тернарные и операции с любым другим количеством операндов: при использовании знаков таких операций в вычислении выражения операция применяется к соответствующему числу последних встретившихся операндов.
Особенности обратной польской записи следующие:
Автоматизация вычисления выражений в обратной польской нотации основана на использовании стека. Об этом говорит сайт https://intellect.icu . Алгоритм вычисления для стековой машины элементарен:
Реализация стековой машины, как программная, так и аппаратная, чрезвычайно проста и может быть очень эффективной. Обратная польская запись совершенно унифицирована — она принципиально одинаково записывает унарные, бинарные, тернарные и любые другие операции, а также обращения к функциям, что позволяет не усложнять конструкцию вычислительных устройств при расширении набора поддерживаемых операций. Это и послужило причиной использования обратной польской записи в некоторых научных и программируемых микрокалькуляторах.
Инфиксное выражение 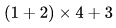 в ОПН может быть записано так: 1 2 + 4 × 3 +
в ОПН может быть записано так: 1 2 + 4 × 3 +
Вычисление производится слева направо, ввод интерпретируется как указано в приведенной ниже таблице (указано состояние стека после выполнения операции, вершина стека выделена красным цветом):
| Ввод | Операция | Стек |
|---|---|---|
| 1 | поместить в стек | 1 |
| 2 | поместить в стек | 1, 2 |
| + | сложение | 3 |
| 4 | поместить в стек | 3, 4 |
| * | умножение | 12 |
| 3 | поместить в стек | 12, 3 |
| + | сложение | 15 |
Результат, 15, в конце вычислений находится на вершине стека.
Клавиша «Ввод» (обозначаемая на калькуляторах как «Enter» или символом «↑») выполняет роль разделителя операндов, когда два операнда непосредственно следуют друг за другом. Если за операндом следует знак операции, то ее нажатие не требуется, это сокращает количество действий, которые нужно выполнить для получения результата.
Эдсгер Дейкстра изобрел алгоритм для преобразования выражений из инфиксной нотации в ОПЗ. Алгоритм получил название «сортировочная станция», за сходство его операций с происходящим на железнодорожных сортировочных станциях. Инфиксная нотация — это форма математических записей, которую использует большинство людей (например, 3 + 4 или 3 + 4 * (2 − 1)). Как и алгоритм вычисления ОПЗ, алгоритм сортировочной станции основан на стеке. В преобразовании участвуют две текстовых переменных: входная и выходная строки. В процессе преобразования используется стек, хранящий еще не добавленные к выходной строке операции. Преобразующая программа читает входную строку последовательно символ за символом (символ — это не обязательно буква), выполняет на каждом шаге некоторые действия в зависимости от того, какой символ был прочитан.
Вход: 3 + 4
Добавим 3 к выходной строке (если прочитано число, то оно сразу добавляется к выходной строке).
Помещаем + (или его Идентификатор) в стек операций.
Добавим 4 к выходной строке.
Мы прочитали все выражение, теперь выталкиваем все оставшиеся в стеке операции в выходную строку. В нашем примере в стеке содержится только +.
Выходная строка: 3 4 +
В данном примере проявляются некоторые правила: все числа переносятся в выходную строку сразу после прочтения; когда выражение прочитано полностью, все оставшиеся в стеке операции выталкиваются в выходную строку.
До тех пор, пока верхним элементом стека не станет открывающая скобка, выталкиваем элементы из стека в выходную строку. При этом открывающая скобка удаляется из стека, но в выходную строку не добавляется. Если стек закончился раньше, чем мы встретили открывающую скобку, это означает, что в выражении либо неверно поставлен разделитель, либо не согласованы скобки.
1) пока на вершине стека префиксная функция…
… ИЛИ операция на вершине стека приоритетнее o1
… ИЛИ операция на вершине стека левоассоциативная с приоритетом как у o1
… выталкиваем верхний элемент стека в выходную строку;
2) помещаем операцию o1 в стек.
Ограничения и модификации
Алгоритм предполагает, что исходная строка корректна (проверяются не все ошибки), и все префиксные/постфиксные функции унарные.
Для операций вроде −x, являющихся как бинарными, так и унарными, нужна модификация: при обнаружении подобной операции система смотрит на предыдущий символ и определяет, чем будет минус, бинарной операцией или унарной функцией. Соответственно, в стеке и ОПЗ нужны разные символы для бинарного и унарного минуса.
Приоритеты:
Вход: 3 + 4 * 2 / (1 − 5)^2 Читаем «3» Добавим «3» к выходной строке Выход: 3 Читаем «+» Кладем «+» в стек Выход: 3 Стек: + Читаем «4» Добавим «4» к выходной строке Выход: 3 4 Стек: + Читаем «*» Кладем «*» в стек Выход: 3 4 Стек: + * Читаем «2» Добавим «2» к выходной строке Выход: 3 4 2 Стек: + * Читаем «/» Выталкиваем «*» из стека в выходную строку, кладем «/» в стек Выход: 3 4 2 * Стек: + / Читаем «(» Кладем «(» в стек Выход: 3 4 2 * Стек: + / ( Читаем «1» Добавим «1» к выходной строке Выход: 3 4 2 * 1 Стек: + / ( Читаем «−» Кладем «−» в стек Выход: 3 4 2 * 1 Стек: + / ( − Читаем «5» Добавим «5» к выходной строке Выход: 3 4 2 * 1 5 Стек: + / ( - Читаем «)» Выталкиваем «−» из стека в выходную строку, выталкиваем «(» Выход: 3 4 2 * 1 5 − Стек: + / Читаем «^» Кладем «^» в стек Выход: 3 4 2 * 1 5 − Стек: + / ^ Читаем «2» Добавим «2» к выходной строке Выход: 3 4 2 * 1 5 − 2 Стек: + / ^ Конец выражения Выталкиваем все элементы из стека в строку Выход: 3 4 2 * 1 5 − 2 ^ / +
Если вы пишете интерпретатор, то выходная строка, полученная после преобразования исходного выражения в обратную польскую нотацию, может храниться вместо исходного выражения для последующей интерпретации. Обратная польская нотация также позволяет компьютеру упрощать выражения.
Рассмотрим алгоритм, который осуществляет предвычисление констант в выражении. Дано выражение в ОПН. Нам понадобится стек для хранения смешанных данных (чисел и операторов).
Алгоритм подобен тому, который применяется для вычисления выражений. Мы просматриваем выражение слева направо.
Пока есть символы для чтения:
После того, как все выражение просмотрено, то, что осталось в стеке, является оптимизированым выражением (операторы выражения лежат в стеке в обратном порядке).
Выражение Инфиксная нотация: exp(-1/2*x) Обратная Польская нотация: -1 2 / x * exp Читаем: «-1» Кладем «-1» в стек Стек: -1 Читаем: «2» Кладем «2» в стек Стек: -1 2 Читаем: «/» Вычисляем частное, результат кладем в стек Стек: -0.5 Читаем: «x» Кладем «x» в стек со значением null Стек: -0.5 x(null) Читаем: «*» Кладем «*» в стек со значением null Стек: -0.5 x(null) *(null) Читаем «exp» Кладем «exp» в стек со значением null Стек: -0.5 x(null) *(null) exp(null) Результат оптимизации: -0.5 x * exp
Данный метод, очевидно, не включает всех возможных способов оптимизации.
В качестве практического применения данной методики можно привести организацию байт-кода конфигураций прикладных решений системы 1С:Предприятие. Официального подтверждения компания 1С не дает, но пользователи данной системы на специализированных форумах приводят доказательства и алгоритмы, позволяющие декомпилировать исходные тексты.
Языки программирования, использующие ОПН в качестве основной:

Инфиксная нотация — операторы записываются между операндами с которыми они взаимодействуют, а в постфиксной нотации (обратная польская запись) операторы записаны после операндов. С теорией, по которой была написана программа, вы можете ознакомиться либо на в разделе информатика, либо читайте переделанный вариант далее.
Для перевода из инфиксной нотации в постфиксную будем использовать переработанный алгоритм Дейкстры. Нам понадобится стек, куда будем записывать математические операторы (программа, которую я приведу далее поддерживает только такие операторы: «+», «-«, «*», «/». Стек я буду использовать тот, который описывался в этой статье (немного модифицированный).
Давайте на примере переведем выражение (1+2)*4. Представим, что элементы выражения это вагоны поезда. Добавим в конец состава поезда вагон с символом «|», который говорит об окончании математического выражения. На схеме представленной ниже есть две станции: первая — Москва, куда попадают операторы, вторая — Киев, где будет формироваться выражение в постфиксной нотации.
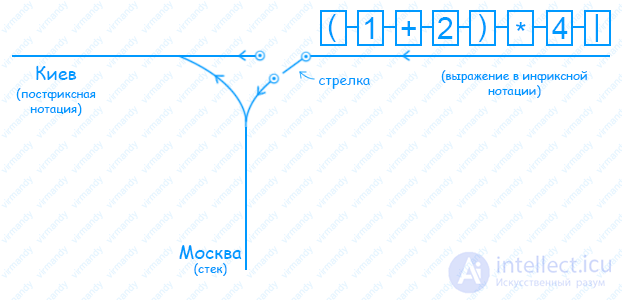
Вагоны содержащие операнды (числа или переменные, в этом примере разбираются только числа) направляются всегда в Киев и никогда не едут в Москву. Вагон с оператором перед стрелкой должен остановиться и узнать куда ему направляться. Для выбора направления давайте рассмотрим следующую таблицу (первая строка соответствует вагонам находящимся на стрелке, левый столбец — предыдущий вагон, отправившийся в Москву):
| | | + | — | * | / | ( | ) | |
|---|---|---|---|---|---|---|---|
| | | 4 | 1 | 1 | 1 | 1 | 1 | 5 |
| + | 2 | 2 | 2 | 1 | 1 | 1 | 2 |
| — | 2 | 2 | 2 | 1 | 1 | 1 | 2 |
| * | 2 | 2 | 2 | 2 | 2 | 1 | 2 |
| / | 2 | 2 | 2 | 2 | 2 | 1 | 2 |
| ( | 5 | 1 | 1 | 1 | 1 | 1 | 3 |
Числа соответствуют следующим ситуациям:
И так, на примере нашего выражения (1+2)*4, давайте смоделируем движение вагонов. Первый вагон попавший на стрелку — «(«, на данный момент в стеке (в Москве) нет никаких элементов, смотрим в табличку, видим, если открывающая скобка идет первой, то отправляем ее в Москву.
| Киев | |
|---|---|
| Москва | ( |
Следующий вагон это число 1, все числа мы без раздумий направляем в Киев.
| Киев | 1 |
|---|---|
| Москва | ( |
Далее идет «+», на данный момент предыдущий вагон, направившийся в Москву это — «(«, смотрим в таблицу, знак сложения после скобки направляется в Москву. Далее число 2 — в Киев.
| Киев | 1 | 2 |
|---|---|---|
| Москва | ( | + |

После идет закрывающая скобка — «)», предыдущий вагон — «+», смотрим в таблицу, видим, что последний вагон направившийся в Москву должен развернуться и направиться в Киев — помещаем наш «+» в Киев (теперь в Киеве у нас такая ситуация: 1 2 +).
| Киев | 1 | 2 | + |
|---|---|---|---|
| Москва | ( |
Внимание, так как не сказано, что вагон с «)» надо куда-то направить, мы снова смотрим в таблицу, теперь последний вагон в Москве — «(«, смотрим в таблицу, видим, что вагоны надо убрать. Удаляем вагон «(» со стека (с Москвы), и перегоняем на стрелку следующий вагон — «*», на данный момент у нас станция Москва пустая, получается что вагон идет первым, смотрим в табличку — знак умножения, если тот первый, направляется в Москву.
| Киев | 1 | 2 | + |
|---|---|---|---|
| Москва | * |
Следующий вагон на стрелке — «4» — в Киев!
| Киев | 1 | 2 | + | 4 |
|---|---|---|---|---|
| Москва | * |
Теперь на стрелку попал последний вагон «|», смотрим в табличку, видим, что если последний вагон в Москве «*», а на стрелке «|», то «*» разворачиваем и направляем с Москвы в Киев.
| Киев | 1 | 2 | + | 4 | * |
|---|---|---|---|---|---|
| Москва |
На стрелке по прежнему остался «последний вагон», в стеке нет ничего, на пересечении «|» и «|» — цифра 4 — преобразование завершено. В Киеве сейчас такая ситуация: 1 2 + 4 *.
С вычислением все гораздо проще. Мы снова будем использовать стек, куда будем помещать все операнды (числа). На примере полученного нами выражения в постфиксной нотации предлагаю провести вычисление. Мы должны перебрать все элементы выражения, числа помещать в стек, а при встрече оператора проводить соответствующее выражение с двумя последними числами в стеке.
| Шаг | ОПЗ | Стек с операндами | |
| Исходные значения | 1 2 + 4 * | ||
| 1 | 2 + 4 * | 1 | |
| 2 | + 4 * | 1, 2 | |
| 3 | 4 * | 3 | Суммируем два последних числа |
| 4 | * | 3, 4 | |
| 5 | 12 | Перемножаем два последних числа |
Теперь пример по сложнее, рассмотрим выражение 8 2 5 * + 1 3 2 * + 4 — /, что в инфиксной нотации соответствует выражению ( 8 + 2 * 5 ) / ( 1 + 3 * 2 — 4 ):
| Шаг | Обратная польская запись | Стек с операндами | |
| Исходные значения | 8 2 5 * + 1 3 2 * + 4 — / | ||
| 1 | 2 5 * + 1 3 2 * + 4 — / | 8 | |
| 2 | 5 * + 1 3 2 * + 4 — / | 8, 2 | |
| 3 | * + 1 3 2 * + 4 — / | 8, 2, 5 | |
| 4 | + 1 3 2 * + 4 — / | 8, 10 | Умножаем 2 на 5 |
| 5 | 1 3 2 * + 4 — / | 18 | Суммируем 8 и 10 |
| 6 | 3 2 * + 4 — / | 18, 1 | |
| 7 | 2 * + 4 — / | 18, 1, 3 | |
| 8 | * + 4 — / | 18, 1, 3, 2 | |
| 9 | + 4 — / | 18, 1, 6 | Умножаем 3 на 2 |
| 10 | 4 — / | 18, 7 | Суммируем 1 и 6 |
| 11 | — / | 18, 7, 4 | |
| 12 | / | 18, 3 | Вычитаем из 7 4 |
| 13 | 6 | Делим 18 на 3 |
Реализация довольна проста, для перевода нам необходимо запрограммировать только таблицу, а для счета — цикл, стек и пара условий. Заголовочный файл, стек и графический интерфейс я разбирать не буду. Про стек можете прочитать здесь. Все исходные коды рабочей программы будут приведены нижу. Начнем пожалуй с перевода из инфиксной нотации в постфиксную. Чтобы упростить себе жизнь элементы математического выражения будем вводить через пробел. Для этого я создал функцию convert, которая в качестве формального параметра принимает строку в инфиксной нотации, а, как результат, возвращает строку в постфиксной нотации:
PHP
|
1 |
|
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
QString MainWindow::convert(QString inf_string){ QStringList inf,post; stk->clear(); inf=(inf_string+" $").split(" ");//разбиваем строку по пробелам int status=2; //Переменная будет иметь 3 состояния: 0 - преобразование не выполнено, ошибка; 1 - преобразование выполнено успешно; 2 - преобразование в процессе int i=0; QString first; //здесь будет храниться последний элемент в стеке while(status==2){ first=stk->get_first_element();//элемент на вершине стека (последний добавленный в стек элемент) QRegExp rx("^\\d+\.?\\d*$"); //шаблон числа if(rx.indexIn(inf[i])==0){ post.append(inf[i]); i++;} //проверка, является ли элемент числом if(inf[i]=="+"||inf[i]=="-"){ //если на стрелке + или - if(first=="-1" || first=="("){ stk->add(inf[i]); i++;} else if(first=="+" || first=="-" || first=="*" || first=="/") post.append(stk->take()); }else if(inf[i]=="*"||inf[i]=="/"){ //если на стрелке * или / if(first=="-1" || first=="(" || first=="+" || first=="-"){ stk->add(inf[i]); i++;} else if(first=="*" || first=="/")post.append(stk->take()); }else if(inf[i]=="("){ stk->add(inf[i]); i++;} //если на стрелке открывающая скобка, то добавляем ее в стек else if(inf[i]==")"){ //если на стрелке закрывающая скобка if(first=="-1")status=0; // если на стрелке закрывающая скобка, а в стеке нет элементов - изменяем стутус на 0 - ошибка else if(first=="+" || first=="-" || first=="*" || first=="/") post.append(stk->take()); else if(first=="("){stk->take(); i++;} }else if(inf[i]=="$"){//если последний элемент if(first=="-1")status=1; //преобразование из инфиксной нотации в постфиксную завершено else if(first=="+" || first=="-" || first=="*" || first=="/")post.append(stk->take()); else if(first=="(")status=0; // если на стрелке последний вагон, а в стеке есть открывающая скобка - ошибка }else status=0; //неизвестный символ } if(status==1)return post.join(" "); else return "0000"; }
float MainWindow::calc(QString postf){ QStringList post; stk_digit->clear(); post=postf.split(" ");//разбиваем строку в постфиксной записи по пробелам float var_1,var_2; for(int i=0;i QRegExp rx("^\\d+\.?\\d*$"); if(rx.indexIn(post[i])==0) stk_digit->add(post[i].toFloat()); else if(post[i]=="+") stk_digit->add(stk_digit->take()+stk_digit->take()); //сложение двух последних элементов else if(post[i]=="-"){ var_2=stk_digit->take(); var_1=stk_digit->take(); stk_digit->add(var_1-var_2);//вычитание из предпоследнего элемента последний } else if(post[i]=="*") stk_digit->add(stk_digit->take()*stk_digit->take());//перемножаем два последних элемента else if(post[i]=="/"){ var_2=stk_digit->take(); var_1=stk_digit->take(); stk_digit->add(var_1/var_2);// деление предпоследнего элемента на последний } } return stk_digit->take(); } |
stk — объект класса stack, который хранит в себе элементы строкового типа данных QString, в данном контексте предназначен для хранения операторов
Счетчик i увеличиваем только в том случае, если вагон, который стоит на стрелке куда-то отправляется (в таблице пункты 1 и 3). Чтоб понять как работает данный код прокомментирую более подробно следующий кусок:
C++
|
1 2 3 4 |
if(inf[i]=="+"||inf[i]=="-"){ //если на стрелке + или - if(first=="-1" || first=="("){ stk->add(inf[i]); i++;} else if(first=="+" || first=="-" || first=="*" || first=="/") post.append(stk->take()); } |
И так, допустим на стрелку пришел вагон с «+». Теперь далее, согласно таблице добавить в стек (отправить в Москву) мы можем только, если на данный элемент стек пустой, либо, если последний добавленный в стек элемент это открывающая скобка «(«. После добавления элемента в стек мы переходим к следующему. За все это отвечает следующая строка: if(first==»-1″ || first==»(«){ stk->add(inf[i]); i++;}. Смотрим снова в таблицу, видим, что если на стрелке «+», а на вершине стека «+», «-«, «*» или «/», то мы элемент на вершине стека (последний добавленный в него элемент) направить в Киев (в строку где формируется обратная польская запись). За это отвечает следующая строка: if(first==»+» || first==»-» || first==»*» || first==»/») post.append(stk->take());.
Теперь вычисление обратной польской записи. Функция calc, в качестве формального параметра принимает строку с выражением в постфиксной нотации, как результат, возвращает число формата float:
PHP
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
float MainWindow::calc(QString postf){ QStringList post; stk_digit->clear(); post=postf.split(" ");//разбиваем строку в постфиксной записи по пробелам float var_1,var_2; for(int i=0;i QRegExp rx("^\\d+\.?\\d*$"); if(rx.indexIn(post[i])==0) stk_digit->add(post[i].toFloat()); else if(post[i]=="+") stk_digit->add(stk_digit->take()+stk_digit->take()); //сложение двух последних элементов else if(post[i]=="-"){ var_2=stk_digit->take(); var_1=stk_digit->take(); stk_digit->add(var_1-var_2);//вычитание из предпоследнего элемента последний } else if(post[i]=="*") stk_digit->add(stk_digit->take()*stk_digit->take());//перемножаем два последних элемента else if(post[i]=="/"){ var_2=stk_digit->take(); var_1=stk_digit->take(); stk_digit->add(var_1/var_2);// деление предпоследнего элемента на последний } } return stk_digit->take(); } |
stk_digit — объект класса stak_digit , который хранит в себе элементы типа данных float, в данном контексте предназначен для хранения операндов.
Далее вы можете скачать программу, которая демонстрирует работу этих функций. В данном примере эти функции являются методами класса MainWindow, по этому я писал вместо float calc(QString postf) — float MainWindow::calc(QString postf).
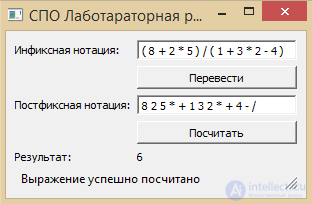
| Инфиксная нотация | Обратная польская запись | Ответ |
| ( 8 + 2 * 5 ) / ( 1 + 3 * 2 — 4 ) | 8 2 5 * + 1 3 2 * + 4 — / | 6 |
| ( 1 + 2 ) * 4 + 3 | 1 2 + 4 * 3 + | 15 |
| ( 15 / 3 + 11 — 3 * 5 ) / 3.2 * ( 5.6 — 10 ) | 15 3 / 11 + 3 5 * — 3.2 / 5.6 10 — * | -1.375 |
Анализ данных, представленных в статье про математические нотации, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое математические нотации, префиксная, инфиксная, постфиксная, обратная польская запись, польская нотация и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Информатика
Комментарии
Оставить комментарий
Информатика
Термины: Информатика