Лекция
Привет, Вы узнаете о том , что такое массив, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое массив, массивы , настоятельно рекомендую прочитать все из категории Алгоритмизация и программирование. Структурное программирование. Язык C.
массив — структура данных, хранящая набор значений (элементов массива), идентифицируемых по индексу или набору индексов, принимающих целые (или приводимые к целым) значения из некоторого заданного непрерывного диапазона. Одномерный массив можно рассматривать как реализацию абстрактного типа данных — вектор. В некоторых языках программирования массив может называться также таблица, ряд, вектор, матрица.
Размерность массива — это количество индексов, необходимое для однозначной адресации элемента в рамках массива. По количеству используемых индексов массивы делятся на одномерные, двумерные, трехмерные и т. д.
Форма или структура массива — сведения о количестве размерностей и размере (протяженности) массива по каждой из размерностей; может быть представлена одномерным массивом .
Особенностью массива как структуры данных (в отличие, например, от связного списка) является константная вычислительная сложность доступа к элементу массива по индексу . Массив относится к структурам данных с произвольным доступом.
В простейшем случае массив имеет константную длину по всем размерностям и может хранить данные только одного, заданного при описании, типа. Ряд языков поддерживает также динамические массивы , длина которых может изменяться во время выполнения программы, и гетерогенные массивы, которые могут в разных элементах хранить данные различных типов. Некоторые специфичные типы массивов, используемые в различных языках и реализациях — ассоциативный массив, дерево отрезков, V-список, параллельный массив, разреженный массив.
Основные достоинства использования массивов — легкость вычисления адреса элемента по его индексу (поскольку элементы массива располагаются один за другим), одинаковое время доступа ко всем элементам, малый размер элементов (они состоят только из информационного поля).
Среди недостатков — невозможность удаления или добавления элемента без сдвига других при использовании статических массивов, а при использовании динамических и гетерогенных массивов — более низкое быстродействие из-за накладных расходов на поддержку динамики и разнородности. При работе с массивами с реализацией по типу языка Си (с указателями) и отсутствии дополнительных средств контроля типичной ошибкой времени выполнения является угроза выхода за границы массива и повреждения данных.
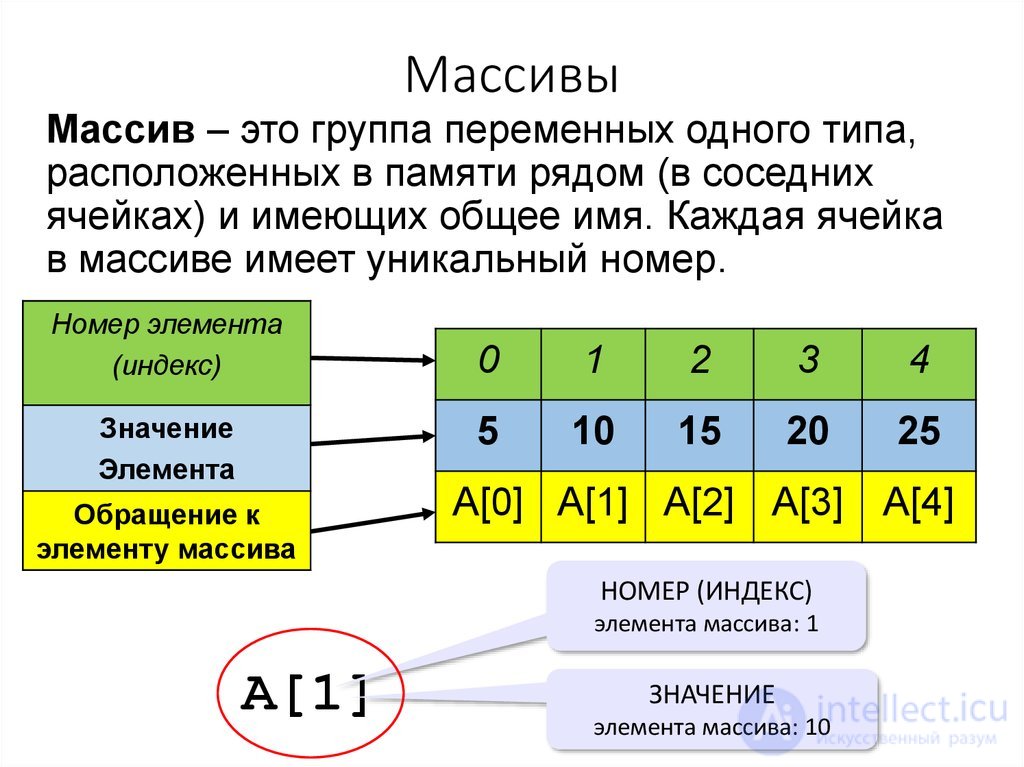
Когда объекты данных хранятся в массиве, отдельные объекты выбираются по индексу, который обычно является неотрицательным скалярным целым числом . Индексы также называются индексами. Индекс сопоставляет значение массива с хранимым объектом.
Существует три способа индексации элементов массива:
0 ( индексация с нуля )
Первый элемент массива индексируется индексом 0.
1 ( индексация на основе единицы )
Первый элемент массива индексируется индексом 1.
n ( индексация на основе n )
Базовый индекс массива может быть выбран свободно. Обычно языки программирования, допускающие индексацию на основе n, также допускают отрицательные значения индекса и другие скалярные типы данных, такие как перечисления или символы , которые могут использоваться в качестве индекса массива.
Использование индексации с нулевой базой является выбором дизайна многих влиятельных языков программирования, включая C , Java и Lisp . Это приводит к более простой реализации, где индекс ссылается на смещение от начальной позиции массива, поэтому первый элемент имеет смещение, равное нулю.
Массивы могут иметь несколько измерений, поэтому не редкость получить доступ к массиву с помощью нескольких индексов. Например, двумерный массив Aс тремя строками и четырьмя столбцами может предоставить доступ к элементу во 2-й строке и 4-м столбце с помощью выражения A в случае системы индексации с нулевой базой. Таким образом, для двумерного массива используются два индекса, для трехмерного массива — три, а для n -мерного массива — n .
Число индексов, необходимых для указания элемента, называется размерностью, размерностью или рангом массива.
В стандартных массивах каждый индекс ограничен определенным диапазоном последовательных целых чисел (или последовательных значений некоторого перечислимого типа ), а адрес элемента вычисляется по «линейной» формуле по индексам.

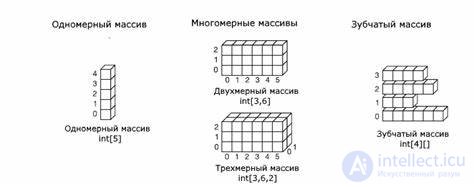
Схема типичного одномерного массива
Одномерный массив (или массив с одним измерением) — это тип линейного массива. Доступ к его элементам осуществляется с помощью одного индекса, который может представлять индекс строки или столбца.
В качестве примера рассмотрим декларацию C int anArrayName[10];, которая объявляет одномерный массив из десяти целых чисел. Здесь массив может хранить десять элементов типа int. Этот массив имеет индексы, начинающиеся от нуля до девяти. Например, выражения anArrayName и anArrayName являются первым и последним элементами соответственно.
Для вектора с линейной адресацией элемент с индексом i расположен по адресу B + c · i , где B — фиксированный базовый адрес , а c — фиксированная константа, иногда называемая приращением адреса или шагом .
Если допустимые индексы элементов начинаются с 0, константа B — это просто адрес первого элемента массива. По этой причине язык программирования C определяет, что индексы массива всегда начинаются с 0; и многие программисты будут называть этот элемент « нулевым », а не «первым».
Однако можно выбрать индекс первого элемента, выбрав соответствующий базовый адрес B. Например, если массив имеет пять элементов, проиндексированных от 1 до 5, и базовый адрес B заменен на B + 30 c , то индексы этих же элементов будут от 31 до 35. Если нумерация не начинается с 0, константа B может не быть адресом какого-либо элемента.
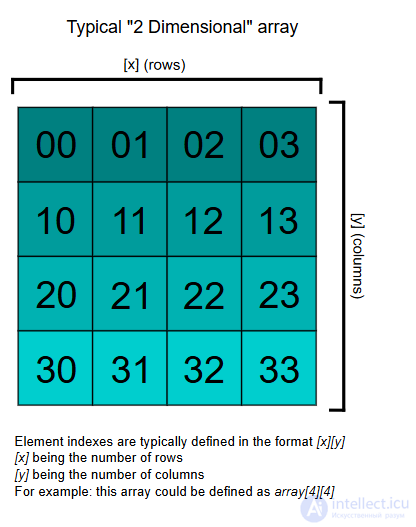
Схема типичного двумерного массива
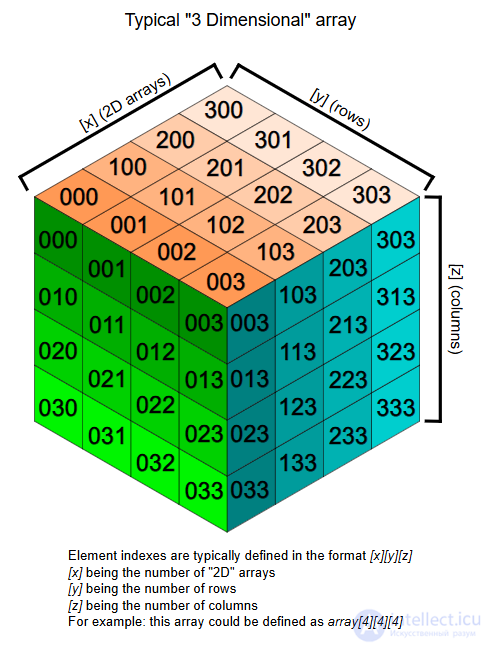
Схема типичного 3D массива
Для многомерного массива элемент с индексами i , j будет иметь адрес B + c · i + d · j , где коэффициенты c и d являются приращениями адреса строки и столбца соответственно.
В более общем случае, в k -мерном массиве адрес элемента с индексами i 1 , i 2 , ..., i k равен

Например: int a ;
Это означает, что массив a имеет 2 строки и 3 столбца, и массив имеет целочисленный тип. Здесь мы можем хранить 6 элементов, они будут храниться линейно, но начиная с первой строки линейно, а затем продолжая второй строкой. Вышеуказанный массив будет храниться как a 11 , a 12 , a 13 , a 21 , a 22 , a 23 .
Эта формула требует только k умножений и k сложений для любого массива, который может поместиться в памяти. Более того, если какой-либо коэффициент является фиксированной степенью 2, умножение можно заменить сдвигом битов .
Коэффициенты c k должны быть выбраны таким образом, чтобы каждый допустимый индексный кортеж соответствовал адресу отдельного элемента.
Если минимально допустимое значение для каждого индекса равно 0, то B — это адрес элемента, все индексы которого равны нулю. Как и в одномерном случае, индексы элементов можно изменить, изменив базовый адрес B. Таким образом, если двумерный массив имеет строки и столбцы, проиндексированные от 1 до 10 и от 1 до 20 соответственно, то замена B на B + c 1 − 3 c 2 приведет к их перенумерации от 0 до 9 и от 4 до 23 соответственно. Используя эту возможность, некоторые языки (например, FORTRAN 77) указывают, что индексы массива начинаются с 1, как в математической традиции, в то время как другие языки (например, Fortran 90, Pascal и Algol) позволяют пользователю выбирать минимальное значение для каждого индекса.
Формула адресации полностью определяется измерением d , базовым адресом B и приращениями c 1 , c 2 , ..., c k . Часто бывает полезно упаковать эти параметры в запись, называемую дескриптором массива, вектором шага или вектором допинга . Размер каждого элемента, а также минимальное и максимальное значения, допустимые для каждого индекса, также могут быть включены в вектор допинга. Вектор допинга является полным дескриптором для массива и удобным способом передачи массивов в качестве аргументов процедурам . Многие полезные операции по нарезке массива (такие как выбор подмассива, обмен индексами или изменение направления индексов) могут быть выполнены очень эффективно путем манипулирования вектором допинга.
Часто коэффициенты выбираются так, чтобы элементы занимали непрерывную область памяти. Однако это не обязательно. Даже если массивы всегда создаются с непрерывными элементами, некоторые операции по нарезке массивов могут создавать из них ненепрерывные подмассивы.
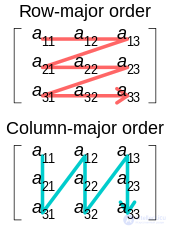
Иллюстрация порядка расположения строк и столбцов
Существуют два систематических компактных макета для двумерного массива. Например, рассмотрим матрицу
А=[123456789].
В компоновке с приоритетом строк (принятой в языке C для статически объявленных массивов) элементы в каждой строке хранятся в последовательных позициях, и все элементы строки имеют меньший адрес, чем любой из элементов последовательной строки:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
В столбцовом порядке (традиционно используемом в Фортране) элементы в каждом столбце располагаются в памяти последовательно, и все элементы столбца имеют меньший адрес, чем любой из элементов последовательного столбца:
| 1 | 4 | 7 | 2 | 5 | 8 | 3 | 6 | 9 |
Для массивов с тремя и более индексами "порядок по строкам" помещает в последовательные позиции любые два элемента, индексные кортежи которых отличаются только на единицу в последнем индексе. Об этом говорит сайт https://intellect.icu . "Порядок по столбцам" аналогичен в отношении первого индекса.
В системах, использующих кэш процессора или виртуальную память , сканирование массива происходит намного быстрее, если последовательные элементы хранятся в последовательных позициях в памяти, а не разбросаны. Это известно как пространственная локальность, которая является типом локальности ссылки . Многие алгоритмы, использующие многомерные массивы, будут сканировать их в предсказуемом порядке. Программист (или сложный компилятор) может использовать эту информацию для выбора между строковой или столбцовой компоновкой для каждого массива. Например, при вычислении произведения A · B двух матриц было бы лучше хранить A в строковом порядке, а B в столбцовом порядке.
Статические массивы имеют фиксированный размер при создании и, следовательно, не позволяют вставлять или удалять элементы. Однако, выделяя новый массив и копируя в него содержимое старого массива, можно эффективно реализовать динамическую версию массива; см. динамический массив . Если эта операция выполняется нечасто, вставки в конец массива требуют только амортизированного постоянного времени.
Некоторые структуры данных массива не перераспределяют память, но сохраняют счетчик количества используемых элементов массива, называемый счетчиком или размером. Это фактически делает массив динамическим массивом с фиксированным максимальным размером или емкостью; строки Pascal являются примерами этого.
Иногда используются более сложные (нелинейные) формулы. Например, для компактного двумерного треугольного массива формула адресации представляет собой полином степени 2.
Массив — упорядоченный набор элементов, каждый из которых хранит одно значение, идентифицируемое с помощью одного или нескольких индексов. В простейшем случае массив имеет постоянную длину и хранит единицы данных одного и того же типа, а в качестве индексов выступают целые числа.
Количество используемых индексов массива может быть различным: массивы с одним индексом называют одномерными, с двумя — двумерными, и так далее. Одномерный массив — нестрого соответствует вектору в математике; двумерный («строка», «столбец») — матрице. Чаще всего применяются массивы с одним или двумя индексами; реже — с тремя; еще большее количество индексов — встречается крайне редко.
Первый элемент массива, в зависимости от языка программирования, может иметь различный индекс. Различают три основных разновидности массивов: с отсчетом от нуля (zero-based), с отсчетом от единицы (one-based) и с отсчетом от специфического значения заданного программистом (n-based). Отсчет от нуля более характерен для низкоуровневых языков программирования, хотя встречается и в языках высокого уровня, например, используется почти во всех языках семейства Си. В ряде языков (Паскаль, Ада, Модула-2) диапазон индексов может определяться как произвольный диапазон значений любого типа данных, приводимого к целому, то есть целых чисел, символов, перечислений, даже логического типа (в последнем случае массив имеет два элемента, индексируемых значениями «Истина» и «Ложь»).
Пример фиксированного массива на языке Паскаль
{Одномерный массив целых чисел. Нумерация элементов от 1 до 15}
a: array [1..15] of Integer;
{Двумерный массив символов. Нумерация по столбцам по типу Byte (от 0 до 255)
по строкам от 1 до 5}
multiArray : array [Byte, 1..5] of Char;
{Одномерный массив из строк. Нумерация по типу word (от 0 до 65536)}
rangeArray : array [Word] of String;
Пример фиксированного массива на Си
int Array[10]; // Одномерный массив: целых чисел, размера 10;
// Нумерация элементов — от 0 до 9.
double Array[12][15]; // Двумерный массив:
// вещественных чисел двойной точности,
// размера 12 на 15;
// Нумерация: по строкам — от 0 до 11,
// по столбцам — от 0 до 14.
В некоторых языках программирования многомерные массивы создаются на основе одномерных, у которых элементы являются массивами .
Пример двумерного массива на JavaScript
//Создание двумерного массива чисел:
var array = [
[11, 12, 13, 14, 15, 16], // Первая строка-массив
[21, 22, 23, 24, 25, 26], // Вторая
[31, 32, 33, 34, 35, 36] // Третья
];
// Вывод массива на консоль:
array.forEach((subArray) => { // Для каждого под-массива,
subArray.forEach((item) => { // для каждого его элемента,
console.log(item); // — вывести этот элемент на консоль.
});
});
Поддержка индексных массивов (свой синтаксис объявления, функции для работы с элементами и так далее) есть в большинстве высокоуровневых языков программирования. Максимально допустимая размерность массива, типы и диапазоны значений индексов, ограничения на типы элементов определяются языком программирования или конкретным транслятором.
В языках программирования, допускающих объявления программистом собственных типов, как правило, существует возможность создания типа «массив». В определении такого типа задаются типы и/или диапазоны значений каждого из индексов и тип элементов массива. Объявленный тип в дальнейшем может использоваться для определения переменных, формальных параметров и возвращаемых значений функций. Некоторые языки поддерживают для переменных-массивов операции присваивания (когда одной операцией всем элементам массива присваиваются значения соответствующих элементов другого массива).
Объявление типа «массив» в языке Паскаль
type
TArrayType = array [0..9] of Integer;
(* Массивы, имеющие заданные параметры:
1. Размер — 10 ячеек;
2. Тип элементов, пригодных для хранения —
— целые числа диапазона [−32 768; 32 767],
— объявляются типом операндов, называющимся "TArrayType". *)
var
arr1, arr2, arr3: TArrayType;
(* Объявление трех переменных-массивов одного типа
(вышеуказанного "TArrayType"). *)
В языке программирования APL массив является основным типом данных (при этом нуль-мерный массив называется скаляром, одномерный — вектором, двумерный — матрицей) . Помимо присваивания массивов в этом языке поддерживаются операции векторной и матричной арифметики, каждая из которых выполняется одной командой, операции сдвига данных в массивах, сортировка строк матрицы.
Динамическими называются массивы, размер которых может изменяться во время выполнения программы. Обычные (не динамические) массивы называют еще фиксированными или статическими.
Динамические массивы могут реализовываться как на уровне языка программирования, так и на уровне системных библиотек. Во втором случае динамический массив представляет собой объект стандартной библиотеки, и все операции с ним реализуются в рамках той же библиотеки. Так или иначе, поддержка динамических массивов предполагает наличие следующих возможностей:
Пример конструкций для работы с динамическими массивами на Delphi:
var // Описания динамических массивов
byteArray : Array of Byte; // Одномерный массив
multiArray : Array of Array of string; // Многомерный массив
...
SetLength(byteArray, 1); // Установка размера массива в 1 элемент.
byteArray[0] := 16; // Запись элемента.
SetLength(byteArray, Length(byteArray)+1); // Увеличение размера массива на единицу
byteArray[Length(byteArray) - 1] := 10; // Запись значения в последний элемент.
WriteLn(byteArray[Length(byteArray) - 1]); // Вывод последнего элемента массива.
...
SetLength(multiArray, 20, 30); // Установка размера двумерного массива
multiArray[10,15] := 12; // Запись значения
SetLength(multiArray, 10, 15); // Уменьшение размера
WriteLn(Length(multiArray), ' ', Length(multiArray[0])
Гетерогенным называется массив, в разные элементы которого могут быть непосредственно записаны значения, относящиеся к различным типам данных. Массив, хранящий указатели на значения различных типов, не является гетерогенным, так как собственно хранящиеся в массиве данные относятся к единственному типу — типу «указатель». Гетерогенные массивы удобны как универсальная структура для хранения наборов данных произвольных типов. Реализация гетерогенности требует усложнения механизма поддержки массивов в трансляторе языка. В ряде языков программирования гетерогенные массивы называются записями.
Типовым способом реализации статического гомогенного (хранящего данные одного типа) массива является выделение непрерывного блока памяти объемом , где S — размер одного элемента, а
— размеры диапазонов индексов (то есть количество значений, которые может принимать соответствующий индекс). При обращении к элементу массива с индексом
адрес соответствующего элемента вычисляется как
, где B — база (адрес начала блока памяти массива),
— значение k -го индекса, приведенное к целому с нулевым начальным смещением. Порядок следования индексов в формуле вычисления адреса может быть различным. (Этот способ соответствует реализации в большинстве компиляторов языка Си; в Фортране порядок индексов противоположен ).
Таким образом, адрес элемента с заданным набором индексов вычисляется так, что время доступа ко всем элементам массива с теоретической точки зрения одинаково; однако, могут сказываться различные значения задержек отклика от оперативной памяти к ячейкам, расположенным на разных элементах памяти, но в практике высокоуровневого программирования такими тонкостями, за редкими исключениями, пренебрегают.
Обычным способом реализации гетерогенных массивов является отдельное хранение самих значений элементов и размещение в блоке памяти массива (организованного как обычный гомогенный массив, описанный выше) указателей на эти элементы. Поскольку указатели на значения любых типов, как правило, имеют один и тот же размер, удается сохранить простоту вычисления адреса, хотя возникают дополнительные накладные расходы на размещение значений элементов и обращение к ним.
Для динамических массивов может использоваться тот же механизм размещения, что и для статических, но с выделением некоторого объема дополнительной памяти для расширения и добавлении механизмов изменения размера и перемещения содержимого массива в памяти.
Также динамические и гетерогенные массивы могут реализовываться путем использования принципиально иных методов хранения значений в памяти, например, одно- или двухсвязных списков. Такие реализации могут быть более гибкими, но требуют, как правило, дополнительных накладных расходов. Кроме того, в них обычно не удается выдержать требование константного времени доступа к элементу.
Размерность массива — это количество индексов, необходимых для выбора элемента. Таким образом, если массив рассматривать как функцию на множестве возможных комбинаций индексов, то это размерность пространства, дискретным подмножеством которого является его домен. Таким образом, одномерный массив — это список данных, двумерный массив — это прямоугольник данных, [ 12 ] трехмерный массив — это блок данных и т. д.
Это не следует путать с размерностью множества всех матриц с заданным доменом, то есть с числом элементов в массиве. Например, массив с 5 строками и 4 столбцами является двумерным, но такие матрицы образуют 20-мерное пространство. Аналогично, трехмерный вектор может быть представлен одномерным массивом размера три.
| Заглянуть (индекс) |
Мутировать (вставить или удалить) в … | Избыточное пространство, среднее |
|||
|---|---|---|---|---|---|
| Начало | Конец | Середина | |||
| Связанный список | Θ( н ) | Θ(1) | Θ(1) — известный конечный элемент; Θ( n ), неизвестный конечный элемент |
Θ( н ) | Θ( н ) |
| Множество | Θ(1) | — | — | — | 0 |
| Динамический массив | Θ(1) | Θ( н ) | Θ(1) амортизированный | Θ( н ) | Θ( n ) [ 9 ] |
| Сбалансированное дерево | Θ(лог n) | Θ(лог n) | Θ(log n ) | Θ(log n ) | Θ( н ) |
| Список случайного доступа | Θ(log n) [ 10 ] | Θ(1) | — [ 10 ] | — [ 10 ] | Θ( н ) |
| Дерево хешированного массива | Θ(1) | Θ( н ) | Θ(1) амортизированный | Θ( н ) | Θ(√ n ) |
Динамические массивы или растущее массивы похожи на массивы, но добавляют возможность вставлять и удалять элементы; добавление и удаление в конце особенно эффективно. Однако они резервируют линейное ( Θ ( n )) дополнительное хранилище, тогда как массивы не резервируют дополнительное хранилище.
Ассоциативные массивы предоставляют механизм для функциональности, подобной массиву, без огромных накладных расходов на хранение, когда значения индекса разрежены. Например, массив, содержащий значения только с индексами 1 и 2 миллиарда, может выиграть от использования такой структуры. Специализированные ассоциативные массивы с целочисленными ключами включают Patricia trys , Judy arrays и van Emde Boas trees .
Сбалансированные деревья требуют O(log n ) времени для индексированного доступа, но также позволяют вставлять или удалять элементы за время O(log n ) , тогда как расширяемые массивы требуют линейного (Θ( n )) времени для вставки или удаления элементов в произвольной позиции.
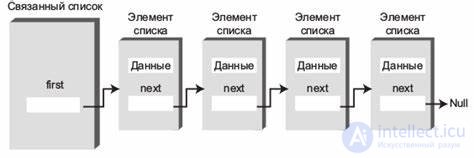
Связанные списки допускают постоянное время удаления и вставки в середину, но требуют линейного времени для индексированного доступа. Их использование памяти обычно хуже, чем у массивов, но все равно линейно.
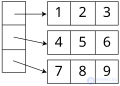
Вектор Илиффе — это альтернатива многомерной структуре массива. Он использует одномерный массив ссылок на массивы на одно измерение меньше. Для двух измерений, в частности, эта альтернативная структура будет вектором указателей на векторы, по одному на каждую строку (указатель на c или c++). Таким образом, элемент в строке i и столбце j массива A будет доступен с помощью двойной индексации ( A [ i ][ j ] в типичной нотации). Эта альтернативная структура допускает неровные массивы , где каждая строка может иметь разный размер — или, в общем случае, где допустимый диапазон каждого индекса зависит от значений всех предыдущих индексов. Это также экономит одно умножение (на приращение адреса столбца), заменяя его битовым сдвигом (для индексации вектора указателей строк) и одним дополнительным доступом к памяти (извлечение адреса строки), что может быть целесообразным в некоторых архитектурах.
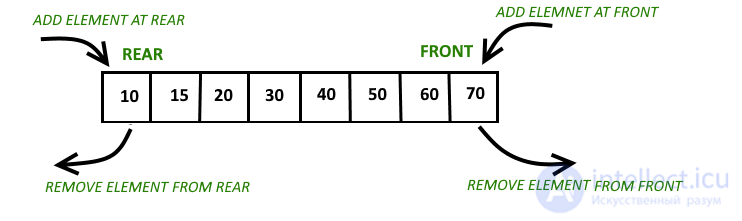
| Характеристика | Очередь (Queue) | Стек (Stack) | Связанный список (Linked List) | Массив (Array) | Дек (Deque) | Куча (Heap) |
|---|---|---|---|---|---|---|
|
Принцип работы
|
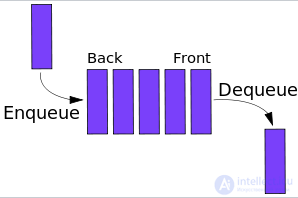
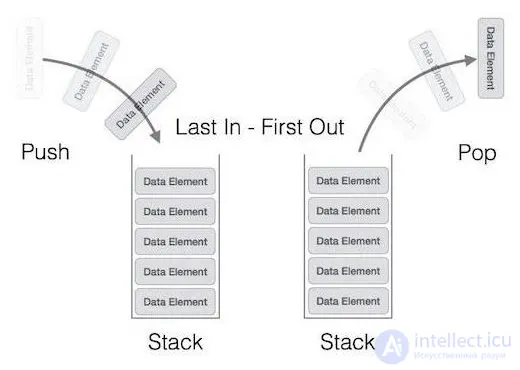
FIFO (первый вошел — первый вышел) | LIFO (последний вошел — первый вышел) | Элементы связаны указателями | Индексы фиксированы | Доступ к обоим концам | Дерево, где родитель >= (max heap) или <= (min heap) дочерних элементов |
|
Добавление элементов
|
В конец (enqueue) | В конец (push) | В начало или конец | В любую позицию | В начало или конец | В корень (с балансировкой) |
|
Удаление элементов
|
Из начала (dequeue) | Из конца (pop) | В любой позиции (требует обхода) | В любой позиции (но требует сдвига) | В начало и конец | Из корня (с перестановкой) |
|
Доступ к элементам
|
Только к первому (head) | Только к последнему (top) | Последовательный (через ссылки) | Прямой доступ по индексу | В начало и конец | Только к корню (наибольший или наименьший элемент) |
|
Время работы (среднее)
|
O(1) (добавление/удаление) | O(1) (добавление/удаление) | O(1) (добавление в начало/конец) | O(1) (доступ), O(n) (вставка/удаление) | O(1) (операции с концами) | O(log n) (добавление, удаление, доступ к корню) |
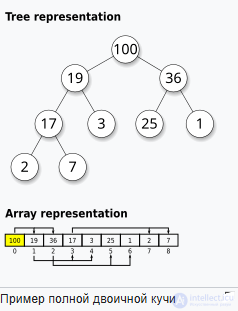
| Где используется | Фоновые задачи, управление потоками, BFS-алгоритмы | Рекурсия, отмена действий (Ctrl+Z) | Динамические структуры, обход графов | Статические структуры, быстрый доступ | Буферы, парсеры, обработка данных | Очередь с приоритетами, алгоритмы Дейкстры и Хаффмана, хранение классов |
 |
 |
 |
 |
 |
 |
Исследование, описанное в статье про массив, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое массив, массивы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Алгоритмизация и программирование. Структурное программирование. Язык C
Комментарии
Оставить комментарий
Алгоритмизация и программирование. Структурное программирование. Язык C
Термины: Алгоритмизация и программирование. Структурное программирование. Язык C